基于多元回歸方法的海洋執法船主尺度分析

李宏偉，管 官

（1.黃海造船有限公司生產設計處，山東榮成 264309；2.大連理工大學船舶工程學院，遼寧大連 116024）

0 引言

隨著海洋經濟的發展，近海及沿海海域海上交通繁忙，海難事故增多，遠海海域與領國間島礁爭端與沖突增多[1]。為維護我國的海洋權益，不僅要壯大我國的海軍力量，還要加強對漁業、海洋巡航的管理與監視，提高海洋權益的維護能力[2]。海洋執法船在維護我國領海主權、維持海上公共秩序、保護海洋環境等方面發揮了重要作用。作為海洋執法船的一種，海監船的主要職能是按照相關法律法規，對我國所管轄的海疆海域進行巡航監視，對破壞海上設施設備、違法違規使用海域、擾亂海上公共秩序、侵犯我國海洋權益等違法違規行為進行查處等；另一類重要的海洋執法船—漁政船是用來在漁業專屬海域進行漁政工作的船舶，主要可用來巡視監督漁場、檢查漁船是否執行與漁業相關的法律法規，防止違規排放污油、廢棄物等有毒有害物質，防止漁民濫捕、維護漁場漁業生產秩序等。海監船和漁船對國家的環境保護、漁業生產、海南救助、主權維護等任務起到了積極的作用[3]。

隨著執法需求的日益增加以及執法復雜程度的提高，業內迫切需要設計和建造噸位大、用途廣、航速高的海洋執法船[4]。近幾年來，我國批建了多艘設備更先進、功能更強大的、用途更廣泛的海洋執法船[5-6]。本文針對海洋執法船的設計特點，采用多元回歸分析方法，對國內外100艘海洋執法船及相近船型的主尺度進行了分析，考慮船舶主尺度與總噸位、排水量等關系的復雜性[7]，將多個變量引入總噸位、排水量回歸模型以提高模型的擬合精度，為海洋執法船后續總體設計提供參考。

1 多元回歸分析

回歸分析是一種傳統應用性較強的科學方法，它通過一組預測變量（自變量）來預測1個或多個響應變量（因變量）[8]。在大多數實際工程問題中，影響因變量的因素通常不止1個，而是多個，一般稱這類問題為多元回歸分析問題。多元回歸分析通過建立因變量與自變量之間的數學模型，對建立的數學模型進行假設檢驗[9]，在符合判定條件的情況下，把給定的自變量數值代入回歸模型，從而計算出自變量的值。多元回歸分析又可分為多元線性回歸分析和多元非線性回歸分析。由于海洋執法船主尺度的復雜性，本文采用多元非線性回歸分析方法，其基本步驟如下。

1）選擇合理的回歸模型。根據回歸分析相關原理，大部分多元非線性回歸問題可轉化為線性回歸問題[10]。線性回歸數學模型表達式見式（1）。

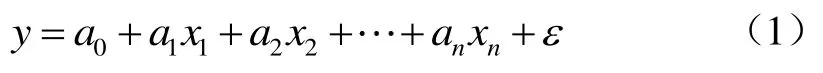
式中：y為因變量；x1,x2,L,xn為自變量；a0,a1,a2,L,an為回歸系數；ε～N(0,σ2)為隨機因素。

2）回歸系數估計。在實際問題中，式（1）中a0,a1,a2,L,an是未知的，需要根據樣本觀察值給出相應的估計值。因此大量準確的樣本資料收集，是得到高擬合度回歸模型的前提。回歸系數的估計值可通過最小二乘法估出，即回歸系數的值應使因變的預測值與真實值的誤差向量達到最小。

3）模型檢驗。數學模型建立后，需要通過數理統計進行檢驗，檢驗模型是否與實際數據有較好的擬合度，判斷模型線性關系的顯著性。常用的統計檢驗有R檢驗、F檢驗和t檢驗等[9]。本文采用F檢驗和t檢驗。其中，F檢驗用于檢驗模型整體回歸關系的顯著性，t檢驗用于檢驗模型中各個回歸系數的顯著性。

2 資料收集

收集大量有效的船型樣本是保證回歸分析順利進行的前提。本文收集到國內外海洋執法船共100艘，噸位從100噸位到8 044噸位，包含了典型的中小型船舶以及大型船舶。國外的樣本大多數取自韓國、日本和美國并以中型、大型船舶為主。各分段噸位內樣本數量的分布狀況如圖1所示。由圖1分析可知，總噸位為400～1 600的船舶數量較多，可知樣本中的中型船舶數量較多，而小型和大型海監船和漁政船的數量相對較少。

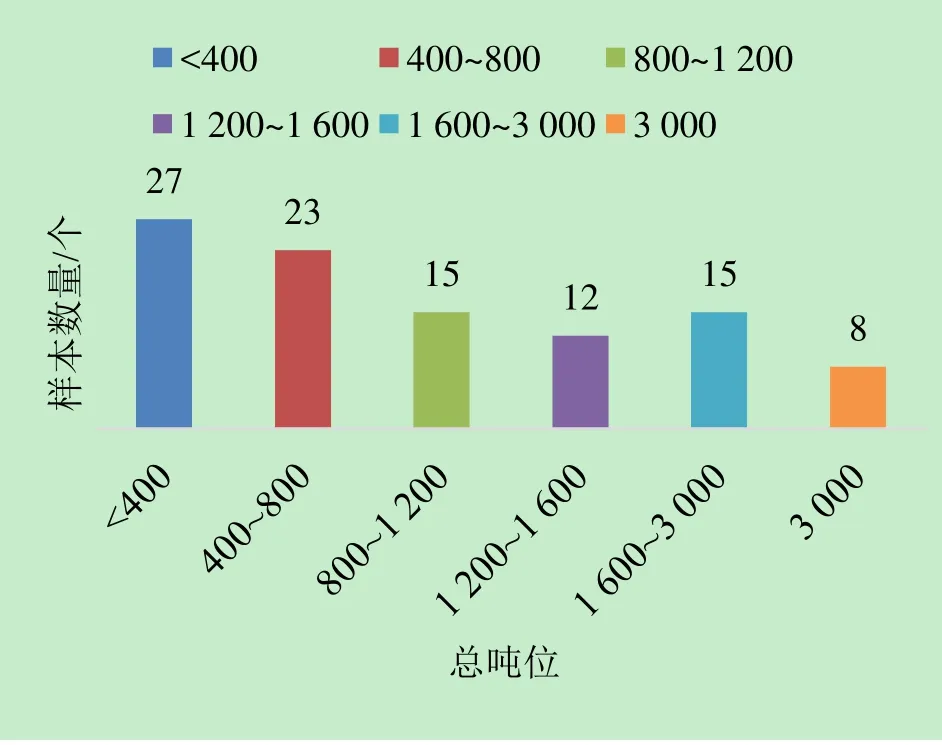
圖1 樣本船噸位分布圖

3 海監船、漁政船主尺度多變量回歸分析

在第2章節中所述樣本的基礎上，分別以排水量和總噸位為因變量，以船舶主尺度包括垂線間長、型寬和型深，建立多元回歸模型。選定了式1中的5個數學模型作為研究基礎，分別對二階多項式、三階多項式以及對數模型采用向后排除法進行了詳細的多元線性回歸分析，即將所有自變量均加入模型中，并對模型進行F檢驗和系數的T檢驗。根據t檢驗結果，從模型中剔除因變量影響相對較小的自變量，再次進行回歸分析，以此類推。每次都保留比前一次分析更好的模型。對每一個公式都進行T檢驗和F檢驗，計算出各個系數的P-value值進行比較。

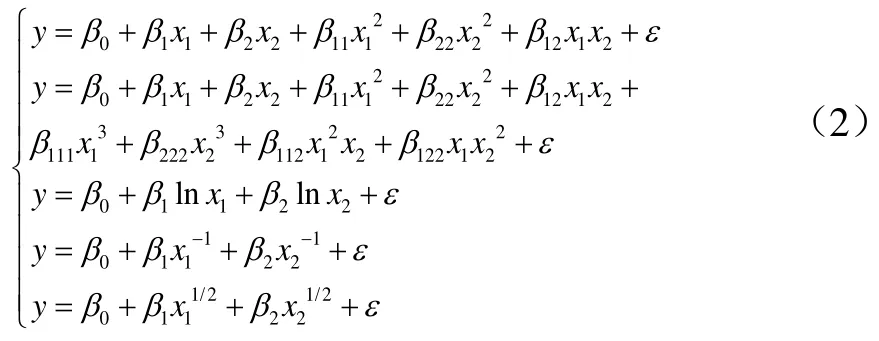
3.1 排水量與垂線間長、型寬的回歸分析

以排水量為因變量，垂線間長和型寬為自變量，建立回歸模型。如式（2）～式（4）所示，y為排水量Δ，x1為垂線間長Lbp，x2為型寬B。式（2）是以二階多項式為基礎的回歸公式，式（3）是以三階多項式為基礎的排水量與垂線間長、型寬的回歸公式。式4是以x1、x2、lnx1、lnx2、x1-1、x2-1、x11/2、x21/2的組合為基礎的排水量與垂線間長、型寬的回歸公式。

3.2 總噸與垂線間長、型寬、型深的回歸分析

以總噸為因變量，垂線間長、型寬和型深為自變量，建立回歸模型，如式（5）～式（8）所示。式中y為總噸位GT；x1為垂線間長Lbp；x2為型寬B；x3為型深D。式（5）是以二階多項式為基礎的總噸與垂線間長、型寬、型深間的回歸公式。式6是以三階多項式為基礎的總噸與垂線間長、型寬、型深的回歸公式。式（7）是以lnx,x-1為基礎總噸與垂線間長、型寬、型深的回歸公式，式8是以lnx為基礎的總噸與垂線間長、型寬、型深的回歸公式。

3.3 多變量回歸結果總結

根據數理統計知識，回歸公式的相關系數越接近1，說明模型的擬合效果越好，而P-value值是F檢驗結果的體現：一般各個系數的P-value越小，說明各個系數的擬合效果越好，一般只要＜2，則認為符合要求。由上述內容可知，以多變量為基礎的回歸公式，其相關系數均＞0.9，P-value值則基本接近于0，說明基于多變量的回歸分析達到了較好的效果。從船舶設計經驗的角度而言，船舶設計本身是一個綜合考慮各項因素的螺旋設計過程，適當增加考慮的因素，更有利于提升船舶的綜合水平。

4 結論

本文以100艘國內外海洋執法船的船型資料為樣本，采用多元回歸分析方法，選取5種典型回歸模型，對樣本主尺度進行了多元回歸分析。建立了以多變量為基礎的數學模型，分析比較了總噸位或排水量與主尺度之間的關系。通過F檢驗和t檢驗，驗證了模型具有良好的擬合效果。提供了多種形式的多變量回歸公式供設計時選擇，為海洋執法船的初步設計提供了參考依據。