雙渠道定價與庫存聯合決策和協調機制選擇

王 敏 李富昌

(云南師范大學 云南 昆明 650500)

一、問題描述與模型

在傳統零售中，批發價格的談判多以制造商為領導，零售商的議價能力比較弱；雙渠道的視角中，批發價格談判不再由制造商單獨決定，零售商業參與議價，作為零售價格與直銷價格在分散決策時處于平等地位。

圖1 雙渠道定價聯合決策協調機制

建設一個雙渠道供應鏈，分為制造商和零售商，商品的生產由制造商負責，并將商品通過線下零售渠道和線上渠道進行銷售。假設1代表線上渠道，2代表線下渠道，制造商的單位生產成本為c，批發價格為l，零售價格為p，直銷價格為d，單位產品在線上渠道成本為k(k>0)，零售商的固定成本為C(包含實體店鋪和運輸成本)，線上渠道銷售占市場總份額的比率為m，商品市場需求為x，消費者對價格的敏感系數為y，利潤為P。所以，制造商線上渠道和零售商線上線下渠道的需求函數是：

f1=mx-yp1

(1)

f2=(1-m)x-yp2

(2)

本文主要研究零售商在線上線下銷售中的主要占比，所以計算出制造商收益、零售商收益和供應鏈總收益：

P1=(l-c)(f1+f2)+f1(d-c)=(l-c)(x-yp1-yp2)+df1-cf1

(3)

P2=(kp1-l)f1+(p2-l)f2-C

(4)

P=P1+P2=(kp1-2c+d)f1+(p2-c)f2-C

(5)

當雙渠道供應鏈聯合機制選擇時，可產生最優決策。在這樣的優化策略中，供應鏈總收益總表達式是式(5)。對式(5)求p1和p2的二階偏導數，可得到目標收益關于p1和p2的Hessian 矩陣為：

(6)

由上可得，目標函數存在唯一解。令式(5)關于p1和p2的一階偏導數等于0，回代求解，得到各項均衡解：

(7)

(8)

得出聯合決策下總供應鏈的最優利潤是：

(9)

由式(9)可以證明，在集中式決策情形下，供應鏈整體收益與k正相關，說明制造商和零售商耗用在線上渠道費用較高，對總供應鏈的利潤造成負擔，所以在雙渠道聯合決策問題上的成本對k的研究應該重點分析，在收益共享契約中達到定價協調策略。

二、基于收益共享契約的定價協調機制選擇決策

建設Stackelberg博弈模型，由于零售商控制雙渠道的總市場，那么其先確定線上和線下的銷售價格，采用逆向歸納法求解，函數表達式為：

l=p1-l1=p2-l2

(10)

第一點求的是制造商確定自己獲得最大利益的價格階段，這個時候制造商的策略函數是：

P1=(l-c)(x-yp1-yp2)=(l-c)(x-(2l+l1+l2)y)

(11)

對l求一階導數并令其等于0，可得到制造商最優價格決策：

(12)

對l求二階導數，存在-4y<0，此時的最優批發價格l*使得制造商的利潤獲得最大值。

(13)

對式(4)分別求p1和p2的二階偏導數，可得到目標收益關于p1和p2的Hessian矩陣是：

(14)

得到制造商在批發價格契約模型下的最優策略：

(15)

由式(15)可知，最優批發價格l*=與參數k正相關。可得到雙方最優決策下的總利潤是：

(16)

三、算例分析

通過理論分析發現渠道成本k對雙渠道供應鏈定價產生重要影響，為了從實證角度進一步證實理論分析的合理性，以及驗證k對其他參數的影響程度，下文通過數值算例對理論模型進行檢驗。假定市場總需求x=100，消費者對價格的敏感系數y=10。

(1)k和m對p1和p2的影響

從表 1 可以看出，線上零售價格p1隨著渠道成本k的降低而逐漸增加，無論是制造商為供應鏈主導者模型下還是零售商為供應鏈主導者模型下，傳統渠道銷售價格高于直銷渠道銷售價格，對于傳統零售商來說，直銷渠道可以節約大量的運輸成本和營銷成本，同時可以減少運輸時間，一定程度上傳統零售商消耗的成本較大。

表1 k和m 對p1的影響

(2)渠道成本k對批發價格的波動情況

從圖2可以看出，隨著渠道成本k的提高，最優批發價格l也在升高，說明當渠道成本增加時，制造商也會通過增加批發價格來緩解成本壓力。

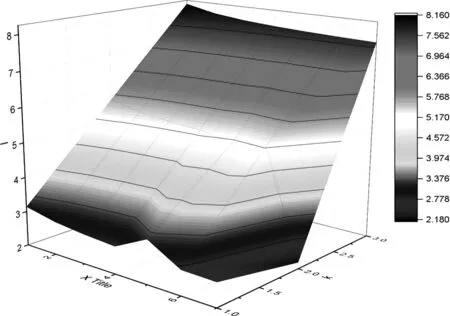
圖2 渠道成本k對最優批發價格l的影響

四、結論

本文得出：在集中式決策情形下，供應鏈整體利潤與k正相關，線上收取的技術服務費費率越低，供應鏈整體利潤就越高；最優批發價與參數k 正相關；價格p1隨著的k增加而降低，隨著m的增加而升高；傳統渠道銷售價格與產品批發價格會隨著直銷渠道的增加而降低。制造商為供應鏈主導者結構下的批發價格與傳統渠道銷售價格，高于零售商為供應鏈主導者結構下的情況。因此，無論是零售商利潤還是制造商利潤，在其為供應鏈主導者時最大。供應鏈總利潤在零售商為供應鏈主導者時最優。本文探討了在單一制造商與單一零售商組成的雙渠道供應鏈結構下，最終實現基于收益共享契約下動態聯合優化策略。