基于魯棒伺服LQR的無人機橫航向自動著陸控制律設計

王利國，矯永康

（1.中航物資裝備有限公司，北京100027；2.海軍航空大學，山東煙臺264001）

無人機高等級自動著陸控制系統是解決進近著陸階段由于地面站人為操作不當而引起飛行事故的最有效方法，其核心之一是設計自動著陸控制律[1]。在著陸期間，無人機必須精確跟蹤期望的著陸軌跡，以使飛機安全、可靠地降落到期望著陸點[2]；另外，著陸期間的不確定因素，包括風擾動和傳感器測量噪聲等，嚴重影響控制精度和飛行安全。因此，著陸軌跡精確控制技術的難點在于如何在外部風擾動及傳感器信號誤差存在的情況下仍能夠保持足夠的控制精度。

現有的解決辦法多是在經典控制架構基礎上，應用魯棒H∞控制技術、模糊控制技術和神經網絡技術設計軌跡跟蹤控制律，取得了一定的應用成果[3-4]，但是這些方法的工程應用前景尚不明確。

應用多變量控制理論魯棒伺服LQR（RSLQR，Robust Servo Linear Quadratic Regulator）設計現代航空飛行器控制律，是波音公司、霍尼韋爾公司、原麥道公司的重要手段和方法[5-7]。該方法兼顧了多個控制目標的控制品質和魯棒特性，在解決現代飛行器多通道耦合、多目標優化等方面，具有較強的優勢[8]。RSLQR方法[9-11]是在LQR 狀態反饋框架的基礎上，將積分環節引入到控制律的前向回路，增強了控制器對外部擾動和不確定性的適應能力，且具備無靜差指令跟蹤能力，能夠滿足自動著陸系統對著陸軌跡跟蹤精度和抗擾動能力的需求[12-14]。

為此，本文從工程應用出發，以提高高附加值無人機高等級自動著陸控制系統的抗干擾能力為目的，研究基于RSLQR的橫側向軌跡跟蹤控制律設計。基于RSLQR方法，設計滾轉姿態保持模態控制律，以此作為控制內回路，分別進行航向保持/預選模態和LOC截獲與跟蹤模態控制律設計。最后，通過單模態數字仿真、RSS分析和蒙特卡洛仿真[15-16]，對基于RSLQR的橫側向軌跡跟蹤控制律進行驗證，為工程應用奠定基礎。

1 橫側向自動著陸過程描述

在有人機精密進近著陸系統的發展中，主要經歷了儀表著陸系統（Instrument Landing System，ILS）、微波著陸系統（Microwave Landing System，MLS）和全球衛星導航自動著陸系統（GBAS Landing System，GLS）等幾個典型階段[1]，其中，現階段應用最為廣泛的是ILS。為了共用機場、跑道等條件，本文以ILS 為對象進行橫側向自動著陸控制律的研究。

ILS自動進場著陸的橫側向控制過程包括LOC波束的截獲過程和波束跟蹤過程。利用航向預選控制模態（通常為45°）把飛機控制到相對于跑道航向的某一角度上，飛機即以這一截獲角飛向跑道中心線。

如圖1所示，當LOC接收機給出的波束偏差信號小于給定值時（一般為2°左右波束偏差μ），LOC 截獲，進入LOC截獲與跟蹤控制，斷開航向預選信號，在航向和波束偏差信號的控制下，無人機將進入并穩定在跑道中心線和跑道航向上。

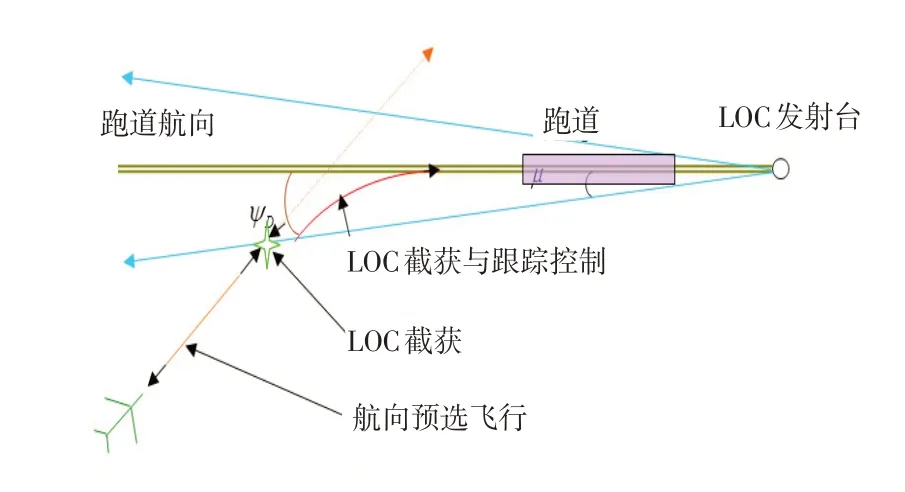
圖1 LOC截獲控制示意圖Fig.1 Sketch of LOC interception control

2 自動著陸控制律設計

根據ILS 橫側向自動著陸過程的描述，橫航向軌跡跟蹤控制律的主要任務有2 個：航向保持/預選和LOC截獲與跟蹤。首先設計基于RSLQR控制技術的滾轉姿態保持控制律，作為航向保持/預選和LOC 截獲與跟蹤模態控制律的內回路。

2.1 滾轉姿態控制模態設計

滾轉姿態保持控制律采用RSLQR[10]方法進行設計，其基本控制結構如圖2所示。

考慮如下基于狀態空間描述的飛機橫航向控制系統：

圖2 RSLQR控制結構Fig.2 Control structure of RSLQR

采用RSLQR控制方法，其控制指令可以寫為：

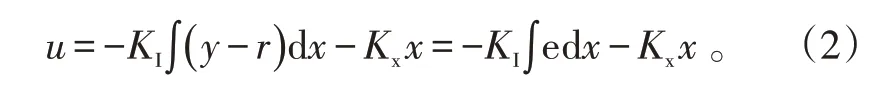
式（2）中，KI、Kx為傳遞系數。

RSLQR 方法是在傳統LQR 方法的基礎上，將跟蹤誤差指令的積分作為一個狀態量進行反饋，使得誤差信號趨向于0，其具有響應快速、魯棒性強、無靜差指令跟蹤的優點，在國內外的導彈和無人機型號上已經取得了成功的應用。圖3 為詳細的基于RSLQR 的滾轉角控制框圖。

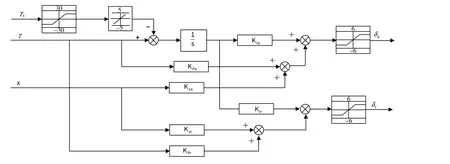
圖3 基于RSLQR的滾轉角控制框圖Fig.3 Block diagram of roll angle control based on RSLQR

2.2 橫航向軌跡精確跟蹤控制律設計

根據圖1的LOC截獲控制示意圖可知，在橫航向截獲前均是采用航向預選模態（通常為45°）把無人機控制到相對于跑道航向的某一角度上，無人機即以這一截獲角飛向跑道中心線，在這個過程中，針對ILS著陸方式，以航向角和LOC信標臺測得的航向波束偏差信號為主要反饋，控制無人機完成航向道的截獲、跟蹤并在預定航向道上穩定飛行。為此，以精確的滾轉角控制為內回路，設計如圖4、5所示的航向保持/預選和LOC截獲與跟蹤模態控制律，實現高等級自動著陸時橫航向軌跡的精確跟蹤。其中：Ψ 為航向角，Ψc為預選航向，LOC偏差的單位為(°)。

圖4 航向保持/預選模態控制框圖Fig.4 Block diagram of course keeping/pre-selected mode

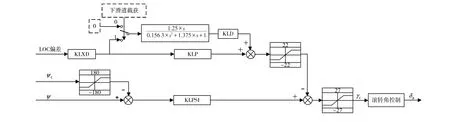
圖5 LOC截獲與跟蹤模態控制框圖Fig.5 Block diagram of LOC interception and tracking mode control

2.3 橫航向軌跡精確跟蹤控制律性能評估

對橫航向自動著陸性能要求和有效性要求如下：

性能要求為接地時起落架離跑道中心線的距離超過21 m 的概率小于10-6；側滑角過大的概率小于10-6。有效性要求為無人機低于500 ft 進場，成功著陸的概率至少95%。

另外，文獻[17]對自動著陸的接地指標進行了說明。理想著陸需滿足的接地要求：橫向接地位置距跑道中心線的距離小于±8 m；接地處滾轉角小于±1°；接地處偏航角小于±5°。可接受著陸需滿足的接地要求：橫向接地位置距跑道中心線的距離小于±21 m；接地處滾轉角小于±2°；接地處偏航角小于±10°。

傳感器誤差、風干擾等不確定性因素會嚴重影響無人機自動著陸的精度。為此，采用RSS[18-19]（Root Sum Square）結合蒙特卡洛仿真方法[17]對設計的自動著陸控制系統進行魯棒性評價。RSS 能夠反映所有模型誤差的影響，對于各種模型誤差的影響可以進行比對分析，獲得最顯著影響誤差，從而對自動著陸控制系統優化設計指明方向。通過RSS 方法分析影響自動著陸控制系統性能的主要因素，并對這些因素進行各種邊界組合，這樣就可以采用標稱情況+主要因素+邊界組合的方法，能夠較為充分地驗證自動著陸系統的性能邊界。

3 數字仿真與分析

以某無人機高度H=100 m，速度v=70 m/s 的著陸狀態點為例，用以研究基于RSLQR 的橫側向自動著陸控制律的魯棒性和動態特性等控制性能。

3.1 仿真參數設計

3.2 單模態仿真分析

根據3.1的控制參數、無人機模型和舵機模型，不考慮傳感器精度的情況下，在5 m/s 側風下對橫航向自動著陸控制律進行仿真，仿真持續至無人機接地時刻，并與采用常規LQR控制方法的自動著陸控制律進行對比，對比結果如圖6所示。

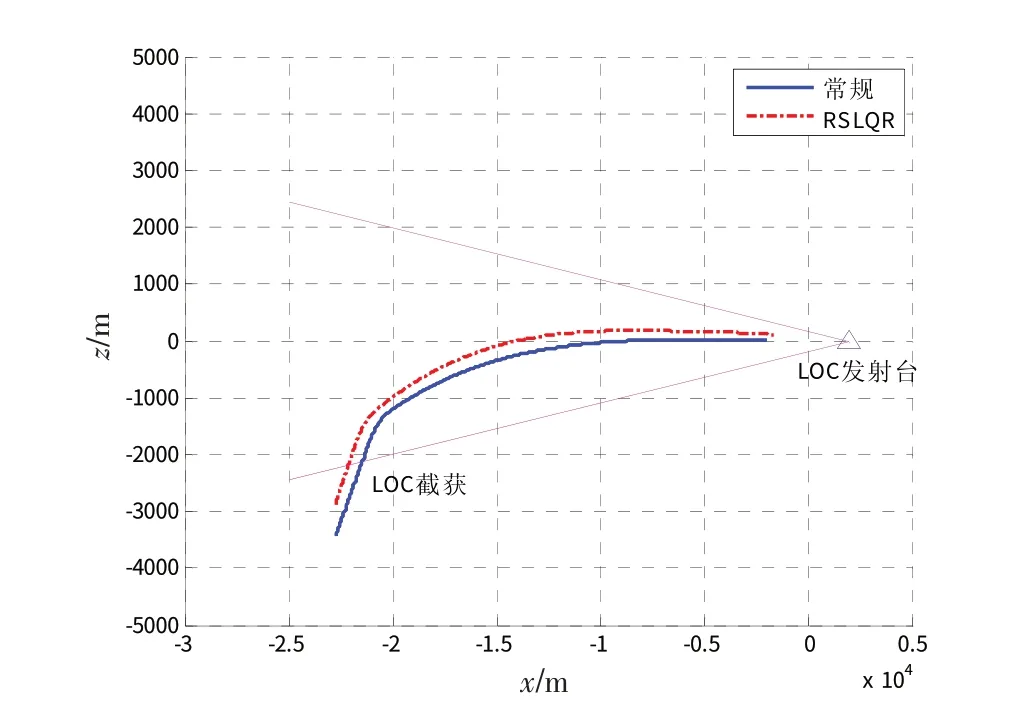
圖6 橫航向自動著陸控制軌跡仿真曲線Fig.6 Trajectory simulation curve of lateral-directional automatic landing control

從圖6中可以看出，基于RSLQR的橫航向自動著陸控制對側風的抑制能力優于常規LQR 控制方法。基于RSLQR方法的著陸過程仿真曲線如圖7所示，從圖中可以看出，整個著陸過程中，側滑角小于1.5°，滾轉角速率小于4(°)/s；接地時刻，無人機橫向接地位置距跑道中心線的距離小于8 m ；接地處滾轉角小于1°；接地處偏航角小于5°，符合自動著陸性能要求和接地指標要求。

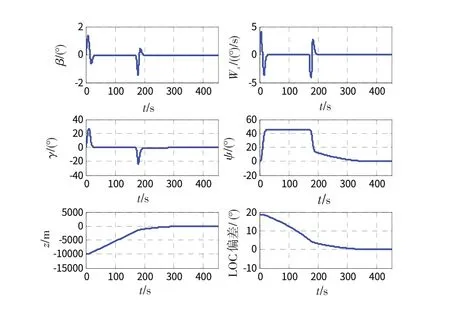
圖7 基于RSLQR的橫航向自動著陸控制仿真曲線Fig.7 Simulation curve of lateral-directional automatic landing control based on RSLQR

3.3 自動著陸控制律魯棒性分析

根據3.1的控制參數、無人機模型和舵機模型，考慮傳感器精度及15 m/s 以內的側風情況，對橫航向自動著陸控制律進行RSS分析和蒙特卡洛仿真。

RSS分析結果見圖8。由圖8可知，影響橫向接地位置的主要因素是LOC 偏差信號精度、側風干擾、航向角和滾轉角偏差，將這4種因素進行排列組合，得到16 種誤差邊界，結合表1 中的誤差源信息，進行1 000次蒙特卡洛仿真，結果見圖9、10。由圖9、10 可知，基于RSLQR 的自動著陸控制律在接地時的滾轉角、偏航角和側向距離方面要優于基于常規控制的自動著陸控制律，說明了基于RSLQR 的自動著陸控制律在魯棒性方面的優勢。

表1 魯棒性分析中誤差源信息Tab.1 Information of error source in robustness analysis

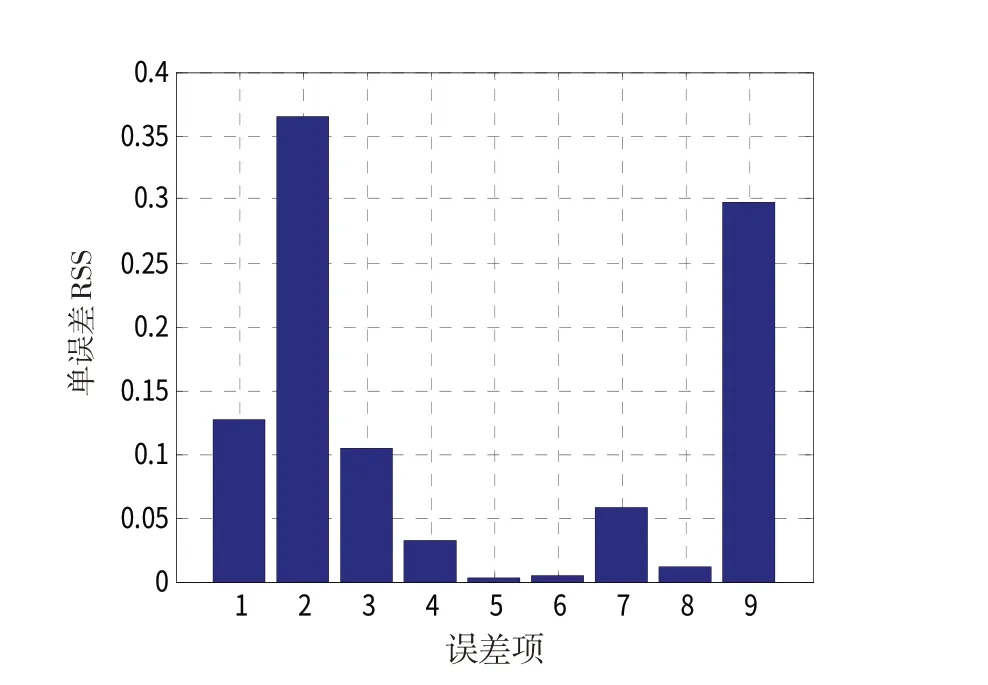
圖8 影響橫向接地位置的RSS分析結果Fig.8 RSS analysis results that affect the horizontal grounding position

圖9 基于RSLQR的自動著陸系統蒙特卡洛打靶結果Fig.9 Monte Carlo shooting results of automatic landing system based on RSLQR

圖10 基于常規控制的自動著陸系統蒙特卡洛打靶結果Fig.10 Monte Carlo shooting results of automatic landing system based on conventional control

4 結論

本文從工程應用出發，研究了一種無人機高等級橫航向自動著陸魯棒控制方法。基于RSLQR方法設計滾轉姿態控制內回路，達到魯棒性強、跟蹤精度高的目標；在此基礎上，設計航向保持/預選模態和LOC截獲與跟蹤模態，實現橫航向軌跡的穩定跟蹤。最后，以某無人機為對象進行了單模態仿真、RSS 分析和蒙特卡洛仿真。結果表明，所設計的自動著陸控制律能夠滿足高等級自動著陸控制的需求，且具有較強的魯棒性。