一類具有產毒浮游植物的交叉擴散浮游生物模型的圖靈斑圖
劉婷婷,彭亞紅
(東華大學 理學院,上海 201620)
我國經濟的日益發展以及人口日漸增多,導致環境遭受的污染越來越嚴重。人們缺乏環境保護的意識,導致水資源惡化嚴重,因此浮游生物大量繁衍暴發的現象頻繁出現。在2007年,中國第三大淡水湖——太湖由于藻類植物的暴發,直接導致水源被嚴重污染,給當地生態環境和淡水養殖業產生了不容小覷的影響。對于此類浮游生物暴發現象,有關學者通過建模,試圖先從理論上對這一問題進行研究[1-4],進而為解決實際問題提供指導。
早在2000—2001年,Chattopadhayay等[5]對浮游植物暴發現象進行實地考察并采集一定數據對此進行分析,根據分析統計的結果,建立了浮游植物釋放毒素的浮游生物模型,如式(1)所示。
(1)
其中:P=P(t)和Z=Z(t)分別為浮游植物種群和浮游動物種群在t時刻的濃度;r和K分別為浮游植物種群的內秉增長率和環境容納量;c為生物量之間的轉化系數;μ為浮游動物種群的自然死亡率;f(P)為浮游植物被浮游動物捕食的函數;g(P)為浮游植物種群釋放有毒物質的函數。
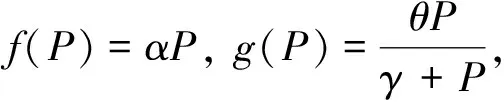
(2)
式中:β=cα;θ為浮游植物種群的毒素釋放率;η為密度制約系數。文獻[1]在模型(2)中引入自擴散系數,并在Neumann邊界條件下考慮如下的擴散模型:
(3)
式中:P=P(x,t),Z=Z(x,t),Ω為具有光滑邊界?Ω的有界區域;v為?Ω的外法單位向量;d1和d2分別為浮游植物和浮游動物的自擴散系數;ΔP和ΔZ分別為P和Z的拉普拉斯算子。假設上述模型中的所有參數均為正常數。
對空間擴散模型(3),文獻[1]先證明了正平衡點是局部漸進穩定的,接著通過構造Lyapunov函數,進一步證明了正平衡點是全局漸近穩定的。
同時,許多學者研究了具有交叉擴散的反應擴散模型的動力學行為[6-11]。而文獻[12-14]的研究表明,交叉擴散項的出現會對模型動力學行為產生影響。本文在文獻[1]的研究基礎上,在模型(3)中引入交叉擴散項,考慮如下模型:
(4)
其中:d11>0,d22>0分別為浮游植物和浮游動物種群的自擴散系數;d12∈R,d21∈R分別為浮游植物和浮游動物種群的交叉擴散系數。涉及的其他參數均為正常數,并假設式(5)成立。
d11d22-d12d21>0
(5)
1 模型(4)正平衡點的穩定性分析
易知,當且僅當
P* (6) 時,模型(4)存在唯一的正平衡點E*(P*,Z*),其中: 定理1不等式(6)成立當且僅當 (7) 證明由于P*是方程 的正根,顯然有式(8)成立。 (8) 又因為P* (9) 成立。 不等式(9)成立當且僅當 (10) 和 (11) 同時成立。 不等式(10)成立當且僅當不等式(8)成立。不等式(11)成立當且僅當 (12) 成立,即式(9)成立當且僅當式(12)成立。從而定理1得證。 引理1(文獻[1]中定理3.2和3.3) (1) 如果模型(3)滿足條件(7),則模型(3)存在唯一的正平衡點E*(P*,Z*),且正平衡點E*是局部漸近穩定的; 由引理1可知,在浮游植物產生有毒物質的浮游生物模型中引入自擴散項之后,該模型的正平衡點仍舊是穩定的,即自擴散項的引入并未引起系統正平衡點穩定性的變化。 令 則模型(2)在E*處的雅可比矩陣為 顯然,a11<0,a12<0,a22<0。由于 所以a21>0。從而有 T0=a11+a22= D0=a11a22-a12a21= 模型(4)在E*處的穩定性由如下特征方程的特征值決定。 λ2-Tkλ+Dk=0,k=0,1,2,… 其中: Tk=[T0-k2(d11+d22)] Dk=D0-k2(a11d22+a22d11-a21d12-a12d21)+ 這里 由Tk的表達式知,對?k≥0,顯然有Tk<0。根據式(5)和D0>0可知,Dk是關于k2的開口向上且截距為正的一元二次多項式,所以可能存在k∈N+,使得Dk<0。這是由于交叉擴散項d12或d21的出現引起的。考慮Dk的對稱軸表達式為 注意到在臨界值 時,Dk取到如下最小值: 模型(3)中,自擴散項的加入未引起正平衡點穩定性的變化,接下來討論模型(4)引入交叉擴散項后正平衡點穩定性的情況。根據上文分析可知,產生圖靈不穩的必要條件為 (13) (14) 式(13)成立當且僅當 (15) 式(14)成立當且僅當 (16) 若式(16)成立,顯然式(15)成立。 定理2假設參數d12,d21∈R,模型(4)中其他參數均為正常數并滿足條件(5)和(7),如果式(16)成立,則模型(4)的正平衡點E*(P*,Z*)是不穩定的。 L1為0.08-d12d21=0 由圖1可知,曲線L1和圖靈分支曲線L2所交區域D1和D2為圖靈不穩區域。其中,D1分布在三、四象限,D2分布在一、四象限,且D1和D2表示如下: D1={(d21,d12)|d12<0,0.08-d12d21>0且 0.172 3d12+0.405 938<0} D2={(d21,d12)|d21>0,0.08-d12d21>0 0.172 3d12+0.405 938<0} 1.1節給出了模型(4)在正平衡點處不穩定的必要條件。模型(4)引入交叉擴散之后,交叉擴散的出現可能會引起系統不穩定的發生,由于模型(4)是在Neumann邊界條件下討論,而波數k是離散的,依賴于Neumann邊界條件,因此,需進一步分析模型(4)的圖靈不穩定的充分條件。為方便起見,在模型(4)中取空間變量為一維,即令Ω=(0,l)。下面分析引起模型(4)正平衡點不穩定的充分條件[12]。 記: (17) 由于d12,d21∈R,根據式(17)可知,存在d12或d21使M<0。 (18) (19) 也即 (20) 成立,其中M由式(17)給出。 由以上分析可得模型(4)的正平衡點不穩定的充分條件,即定理3。 定理3假設d12,d21∈R,模型(4)的其他參數均為正常數并滿足條件(5)和(7)以及式(15)和(16),若存在正整數n,使得式(20)成立,則模型(4)的正平衡點E*(P*,Z*)是不穩定的。 為了驗證定理3中滿足條件的正整數n存在,下面舉例說明。 根據曲線l1和曲線l2表達式可知,當取d21=2時,n1=0.223 6,n2=1.277 9,則取到一個n=1滿足式(19)。 通過以上理論分析,得知模型(4)在引入交叉擴散項之后出現圖靈不穩。在d21-d12平面上,得到不穩定區域D1和D2。本節對不穩定區域及其他區域進行數值模擬。由于浮游植物種群和浮游動物種群模擬出的斑圖類型是類似的,所以在下文的數值模擬中,僅對浮游植物種群進行模擬。 在上文分析中已經得知模型(4)的圖靈不穩定是由交叉擴散系數d12或d21引起的,在接下來的數值模擬中,固定r=1.5,K=17,α=0.063,β=0.038 7,μ=0.035,η=0.09,θ=0.1,γ=1.5,d11=0.4,d22=0.2。d12和d21取不同數值,在圖1中取點驗證。 (1) 固定d12=-7.5,取d21=2.35,0.029進行數值模擬,結果分別如圖2和圖3所示。 在圖1中取(d21,d12)=(2.35,-7.5),該點在d21-d12平面的第四象限中,且在穩定區域中。由圖2可知,隨著時間變化,模型很快出現穩定狀態。 在圖1中取(d21,d12)=(0.029,-7.5),該點在不穩定區域D1中。由圖3可知,隨著時間變化,底部變為黃色區域,在黃色區域中出現大量的藍色點狀斑圖,再經過一段時間的變化,最終穩定下來形成點條型斑圖。 (2) 固定d21=2.499,取d12=-0.46和1.222進行數值模擬,結果分別如圖4和5所示。 在圖1中取(d21,d12)=(2.499,-0.46),該點在不穩定區域D2中。由圖4可知:起初出現無規律的紫色塊狀,隨著時間的延長,開始隱約出現條狀和點狀的斑點;隨著時間再進一步延長,點狀和條狀逐漸明顯,并且點狀斑圖連接成條狀,最終,基本上以條狀斑圖穩定下來。 在圖1中取(d21,d12)=(2.499,1.222),此點在不穩定區域D2上方的區域中。由圖5可知,隨著時間延長先出現一些不規則的紅色斑點,但模型很快出現穩定狀態。 本文主要討論了交叉擴散對具有產毒浮游植物的浮游生物系統穩定性的影響,與僅含有自擴散項的浮游生物模型對比,交叉擴散項d12或d21的出現引起圖靈不穩。在數值模擬部分,分別固定交叉擴散系數d12(改變d21的取值)和d21(改變d12的取值),發現交叉擴散系數d12或d21中任一個量的改變都會引起圖靈不穩定性發生,從而產生豐富的圖靈斑圖,如點條混合斑圖或條狀斑圖。同時,穩定性區域的模擬結果與理論結果也是一致的。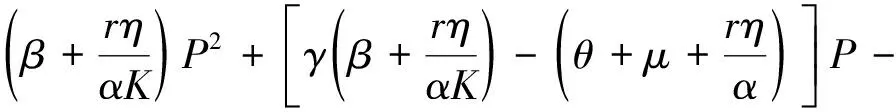
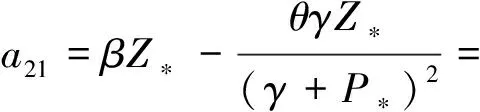
k4(d11d22-d12d21)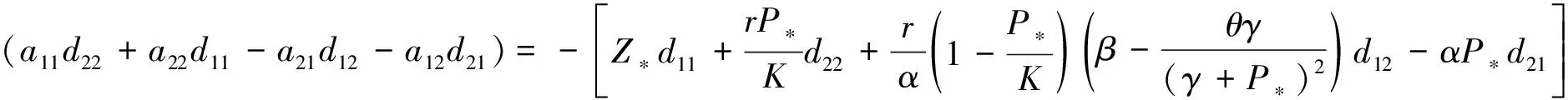
1.1 圖靈不穩定的必要條件
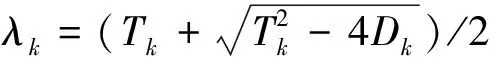
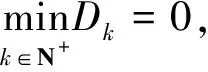
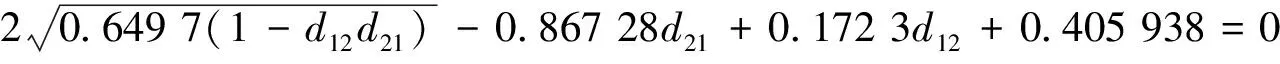
1.2 在有界區間中圖靈不穩定的充分條件
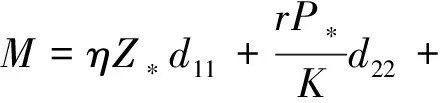
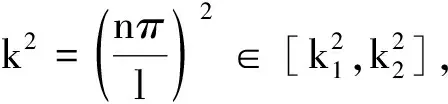
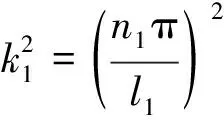
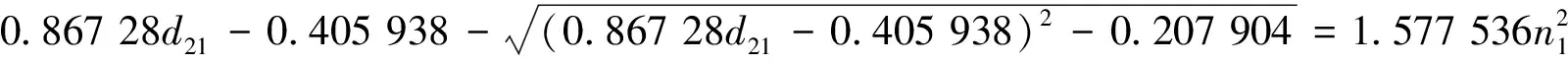
2 數值模擬
3 結 語

