基于SAE-GA-SVM模型的雷達新型干擾識別

羅彬珅,劉利民,董 健,劉璟麒

(陸軍工程大學 電子與光學工程系,石家莊 050003)

0 概述

隨著軍事科技的不斷發展,在信息化戰爭中,電子戰(Electronic Warfare,EW)[1]已經成為引人注目“第四維戰場”,是現代化戰爭中一種特殊的作戰方式,也是一種重要的作戰手段[2]。作為電子對抗中的一個關鍵組成部分,雷達對抗也因電子技術的快速發展而日漸激烈。干擾與抗干擾技術相互制約和互相發展,循環往復,具備在復雜電磁環境下的生存作戰能力已成為未來電子裝備發展的主要方向之一,干擾識別是雷達對抗過程中重要一步。近年來,數字射頻存儲(Digital Radio Frequency Memory,DRFM)[3]技術發展不斷成熟,使得有源欺騙干擾成為當代電子干擾的主要手段。

雷達的有源干擾識別主要有信號接收、預處理、特征提取與降維以及分類識別,最關鍵的步驟是特征提取和分類識別。從信號級層面,利用數字信號處理方法根據信號統計特性找出具有表征信號間差異性的特征。文獻[4]針對頻譜彌散(Smeared Spectrum,SMSP)干擾和切片組合(Chopping and Interleaving,C& I)干擾類型的識別問題,提出了基于雙譜分析和分形維數[5]的干擾識別方法,在一定的干噪比條件下,通過支持向量機(SVM)分類器能夠較為穩定地識別不同干擾類型。文獻[6]針對距離拖引干擾(RGPO)、速度拖引干擾和距離-速度同步拖引干擾的識別問題,提出了基于棧式稀疏自編碼器(Stacked Sparse Autoencoder,SSAE)的有源欺騙干擾識別算法。文獻[7]建立了欺騙式干擾和目標回波數學模型并進行分析和仿真,構建了抗欺騙式干擾特征參數集,通過仿真和外場試驗對提取的部分特征進行了驗證。文獻[8]針對多種新型干擾的識別問題,采用多域聯合的特征提取方法進行干擾類型識別,但未考慮對高維數據進行降維處理。文獻[9]針對多種類型的拖引干擾的識別,采用基于Fisher準則的特征選擇方法進行降維處理,實現了較優的特征子集組合。文獻[10]研究了混合主成分分析(Principal Component Analysis,PCA)與遺傳算法(Genetic Algorithm,GA)的特征降維方法,利用PCA-GA-SVM檢測模型進行雷達輻射源信號識別。

總體來看,雷達有源干擾識別技術還有待進一步完善。目前針對單一干擾類型的識別技術不斷涌現,但是關于新型干擾、多種干擾相結合的復合干擾研究還不全面[11]。多數文獻僅是單純地針對雷達干擾類型的識別研究,而未考慮加入回波信號后的識別情形,不符合現實中的雷達對抗需求,且主要集中在選取有效的干擾信號特征。此外,多數文獻不采用或直接采用傳統的降維處理方法,這樣通過線性映射只能學習到數據的低維結構,不能完全表征其本質特征。

本文對頻譜彌散干擾、切片干擾、靈巧噪聲干擾、噪聲調幅-距離欺騙加性復合干擾與噪聲調頻-距離欺騙加性復合干擾共5種干擾類型,加入回波信號進行識別檢測。通過建立目標回波與干擾信號的數學模型,結合分形理論與信息熵的思想,在時域、頻域、小波域、雙譜域上采用基于多域聯合的方法提取信號特征,并通過堆疊自編碼器(Stacked Autoencoder,SAE)對多維特征實現非線性的降維處理。采用遺傳算法對支持向量機進行參數優化和調整,構建基于SAE-GA-SVM的雷達有源干擾信號的檢測模型。

1 信號建模

根據雷達是否受到干擾以及受到干擾的類型,雷達信號的檢測模型為:

(1)

其中,H0表示未受干擾,H1～H5表示檢測到干擾信號,w(t)表示接收到的信號,Sr(t)表示雷達回波信號,n(t)表示高斯白噪聲,JSMSP(t)表示頻譜彌散干擾,JC& I(t)表示切片組合干擾,JSN(t)表示靈巧噪聲干擾,JAM-RD(t)表示噪聲調幅-距離欺騙干擾,JFM-RD(t)表示噪聲調頻-距離欺騙干擾。

2 堆疊自編碼網絡模型

2.1 自編碼器

自編碼器(Autoencoder,AE)是由HINTON[12]于2006年提出的一種用于學習高效編碼的人工神經網絡,主要包括編碼部分和解碼部分[13]。

1)編碼階段

首先將輸入進行經過標準化處理,可以提高運算精度,加快求解速度。設標準化后的特征輸入向量為x=(x1,x2,…,xn),xi∈[0,1],經過式(2)加權后的到隱藏層的值為h=(h1,h2,…,hm)。

h=f(Wx+b)

(2)

2)解碼階段

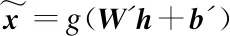
(3)

(4)

式(4)稱為均方誤差(Mean Squared Error,MSE),通常會在代價函數中增加一個權重衰減項,目的是解決AE中的過擬合問題,最后得到的表達式如下:

(5)

其中,λ為權重衰減項的比重,nl為AE的層數,sl為每層神經元的個數。確定自編碼器目標函數后,通過梯度下降算法進行參數θ={W,b}修正:

(6)

(7)

其中,α為學習率。通過迭代運算不斷更新權值矩陣W和偏置矩陣b,完成網絡訓練。

2.2 堆疊自編碼器

堆疊自編碼器包含多個隱藏層,能夠學到更復雜的高維數據。通過逐層訓練的方式,將前一層的輸出作為下一層的輸入。深度自編碼器的每兩層網絡稱為一個限制玻爾茲曼機(Restricted Boltzmann Machine,RBM)[14]。主要包含預訓練過程、展開過程、微調過程3個步驟。

1)預訓練過程

設置網絡結構N1-N2-N3-N2-N1,其中,Ni代表每層數據的維度。利用梯度下降算法根據輸入數據訓練每層的RBM,最后得到每層的權值矩陣W。

2)展開過程

根據預訓練的結果,將預訓練后的RBM連接起來并對稱展開得到堆疊自編碼器,將每層的訓練的權值W作為堆疊自編碼的網絡的初始值,解碼器每層的權值為對應編碼器層數權值的轉置。

3)微調過程

基于重構的誤差函數最小化原則,利用反向傳播(Back Propagation,BP)算法,通過最小化交叉熵函數[15],對初始值W與偏差進行權值微調,交叉熵值越小說明由約簡后的屬性重構原指標數據的誤差越小,最終得到最優網絡結構參數,數據由N1維有效降維到N3維。

(8)

3 GA-SVM算法的雷達有源干擾分類

3.1 支持向量機

支持向量機(SVM)是文獻[16]提出的一種基于統計學習理論的分類方法,其基本思想是在空間中尋求最優分類面w′x+b=0,使線性樣本(xi,yi)正確分離且間隔最大,從而轉換為對一個凸二次規劃問題的求解。通常樣本往往是非線性且不可分的,需引入懲罰因子C與松弛因子ξi,得到式(9):

(9)

使用Lagrange函數及對偶問題,得到最優超平面為:

(10)

進一步引入核函數,使得非線性、不可分的樣本最終能夠成功分離。徑向基核函數(Radial Basis Function,RBF)相比于線性核能夠處理分類標注和屬性的非線性關系,相比于多項式核有更少的參數,同時具有簡單實用、普適性好的優點[17]。本文選取RBF來建立SVM模型,最終得到優化模型如下:

(11)

3.2 遺傳算法參數優化

遺傳算法是由HOLLAND等人[18]于1975年提出的一種基于生物遺傳和進化機制的自適應全局優化搜索方法。該方法具有搜索過程簡單、不易陷入局部最優解、尋優效率高等優點。利用遺傳算法對SVM參數(懲罰因子C和核函數參數g)進行優化,首先進行參數編碼,然后以平均識別率為適應度函數,通過選擇、交叉和變異3個基本運算尋找最優值,最后得到優化后的參數模型。基于SAE-GA-SVM的雷達有源干擾的識別流程如圖1所示。

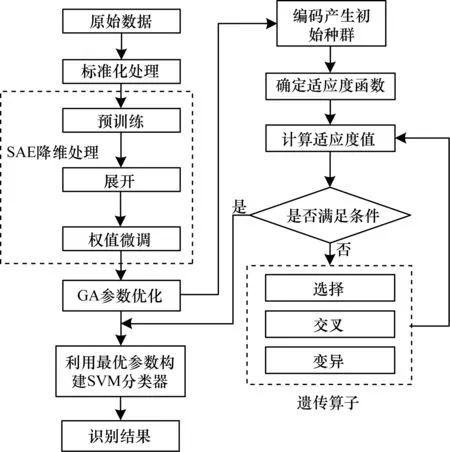
圖1 基于SAE-GA-SVM的雷達有源干擾識別流程

4 仿真結果與分析

4.1 仿真實驗設置

仿真實驗中計算機配置為CPU i3-3227,內存為2 GB,在Windows 7 操作系統下使用MATLAB 2015b進行編碼,SVM分類器算法設計采用LIBSVM庫[19]。

4.1.1 干擾信號參數設置

設置雷達回波信號調制類型為LFM,電壓幅值為1 V,真實目標距離為20 km,假目標距離為25 km,頻率帶寬為10 MHz,中心頻率為1 MHz,脈寬為5 μs,脈沖時間間隔為50 μs,采樣頻率為33 MHz。SMSP干擾分為5段;C& I干擾分為5段,每段2個時隙;靈巧干擾中的卷積噪聲功率為-15 dBw;噪聲調幅-距離復合干擾噪聲功率為23 dB,中心頻率為6 MHz;噪聲調頻-距離復合干擾噪聲功率為15 dBw,調頻指數為0.6,中心頻率為6 MHz。

結合信息熵與分形理論的思想,采用基于時域、頻域、小波域、雙譜域的多維特征提取方法,提取特征T={t1,t2,…,t47}共47維,具體如表1所示。

表1 多域聯合提取的特征類別

4.1.2 數據預處理

本文首先對數據采用標準化處理,使得各屬性特征處于同一數量級,有利于加快計算速度,得到更準確的分類識別效果。根據式(12)將采樣數據線性映射到[0,1]范圍[22]。

(12)

4.2 仿真實驗

4.2.1 基于多維特征提取的雷達干擾類型識別

針對以上提出的6種雷達信號,分別提取如表1所示的47維特征T={t1,t2,…,t47}。設置干噪比(JNR)的范圍為-12 dB,-10 dB,…,6 dB,干噪比間隔為2 dB。通過蒙特卡洛仿真每個干噪比下產生600個訓練樣本,取其中的200個樣本用于測試,并通過基于RBF的SVM分類器,重復進行仿真實驗100次,取其均值作為仿真實驗結果,識別結果如表2所示。由表2可以看出,各類干擾信號的識別率隨JNR增大而呈現上升趨勢。其中,復合噪聲類干擾的識別率較高,能夠接近100%的準確率。當JNR小于-8 dB時,切片重構干擾和目標回波信號的識別率明顯下降,主要是因為高斯白噪聲功率過大,從而導致切片重構干擾信號和目標回波間的特征參數差異性變小,影響了對這兩種信號類型的識別。當JNR大于-6 dB時,各類干擾有90%以上的識別率。

表2 各類干擾信號的識別率

4.2.2 第1隱藏層節點數對SAE的影響

為提高對各干擾的識別率以及有效降低特征維度,本文針對SAE的特征降維效果做了相關的仿真及結果分析,SAE的參數結構對分類識別效果有重要的影響。根據提取的47維特征向量,設定2層RBM進行數據降維處理。輸入層的節點數為47,而第1隱藏層節點數選取非常關鍵,是對原始數據的首次約簡,決定了輸入層特征的抽取能力。一方面,節點數增多能夠加強網絡的學習能力;另一方面,節點數的增多會影響網絡的泛化能力,出現過擬合的問題,并且也會大幅增加計算量。根據4.2.1節的仿真實驗結果,在設置JNR=-10 dB的條件下,通過蒙特卡洛仿真實驗對6種信號類型產生600個訓練樣本,隨機抽取200個作為測試集,重復進行100次仿真實驗,取其均值作為仿真實驗結果,SAE-SVM模型參數設置具體如表3所示。

表3 SAE-SVM 參數設置

為測試第1隱藏層的節點數如何影響分類效果以及改變第1隱藏層的節點數。在微調過程中,SAE利用回饋網絡來微調網絡的權重,從而使降維后的數據能夠更加精準。本文采用47-60-10的結構模型,改變第1隱藏層的節點數。對于不同的SAE結構,微調過程的重構均方誤差(Mean-Square Error,MSE)、信號的平均識別率以及平均訓練時間如表4所示。從表4可以看出,隨著迭代次數的增加,均方誤差通過交叉熵函數的不斷調整而變小。迭代次數在20以內,均方誤差降低的效果最為明顯,最后在80次之后趨于穩定。設置的7種SAE結構在迭代次數為100時的MSE值為0.05左右,實現了較好的擬合效果。從信號識別率來看,先是隨節點數增加而升高,然后趨于降低,其中在節點數為60處有最高的正確識別率。從模型的訓練時間來看,與第1隱藏層的節點數成正比,但從總體上看各個結構模型的訓練時間差異不大。通過綜合考慮,最后選擇第1隱藏層的節點數為60。

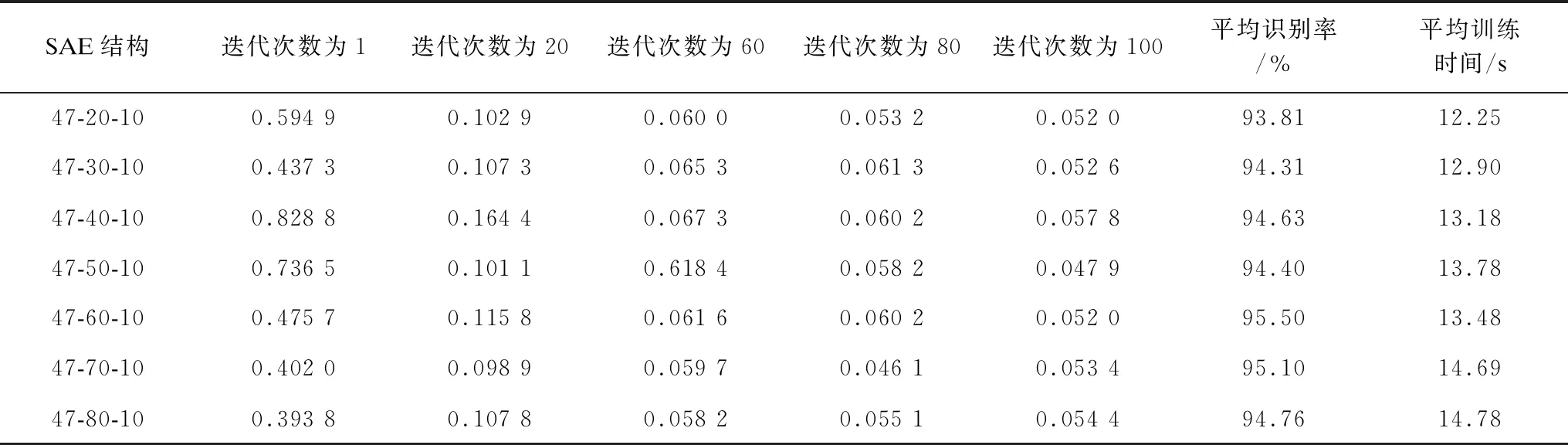
表4 第1隱藏層節點數對SAE性能的影響

4.2.3 輸出層節點數對SAE的影響

自編碼網絡的目的是實現數據的有效降維,在保證識別精度的前提下數據的維度越低,自編碼網絡降維的效果越好。本文研究重點是選擇合適的輸出層節點數,測試輸出層的節點數對SAE性能的影響,本文采用47-60-10的結構模型改變輸出層的節點數,得到不同SAE結構的平均識別率和平均訓練時間,如表5所示。從表5可以看出,一方面隨著輸出層節點數的增加,SAE模型的平均識別率先增加再趨于降低。當輸出層節點數為10時,平均識別率最大值為95.50%。另一方面,表5中10種SAE結構的平均訓練時間大致相同。綜合考慮節點數與平均訓練時間、平均識別率的關系,選取節點數為10的輸出層結構,最終構建的SAE網絡結構為47-60-10。

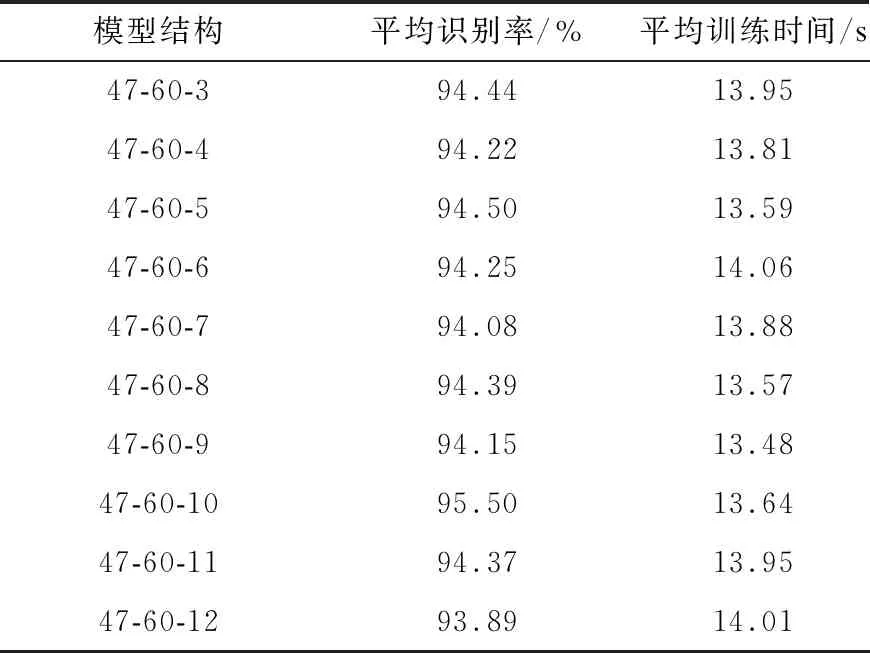
表5 輸出層節點數對SAE性能的影響

4.2.4 GA-SVM雷達有源干擾信號分類模型構建

根據4.2.1節的仿真實驗設置,SVM選用普適度較好的RBF核函數。為提高SVM的分類效果,本文采用GA算法對其進行參數尋優。利用LIBSVM中的gaSVMcgForClass函數來實現優化SVM參數(懲罰因子C和核函數參數g)。GA的相關設置如下:最大進化代數為200,種群數量為20,懲罰因子C的取值范圍為[0,10],核函數參數g的取值范圍為[0,10],交叉驗證次數V=5,交叉概率為0.8。尋優過程的適應度曲線如圖2所示。

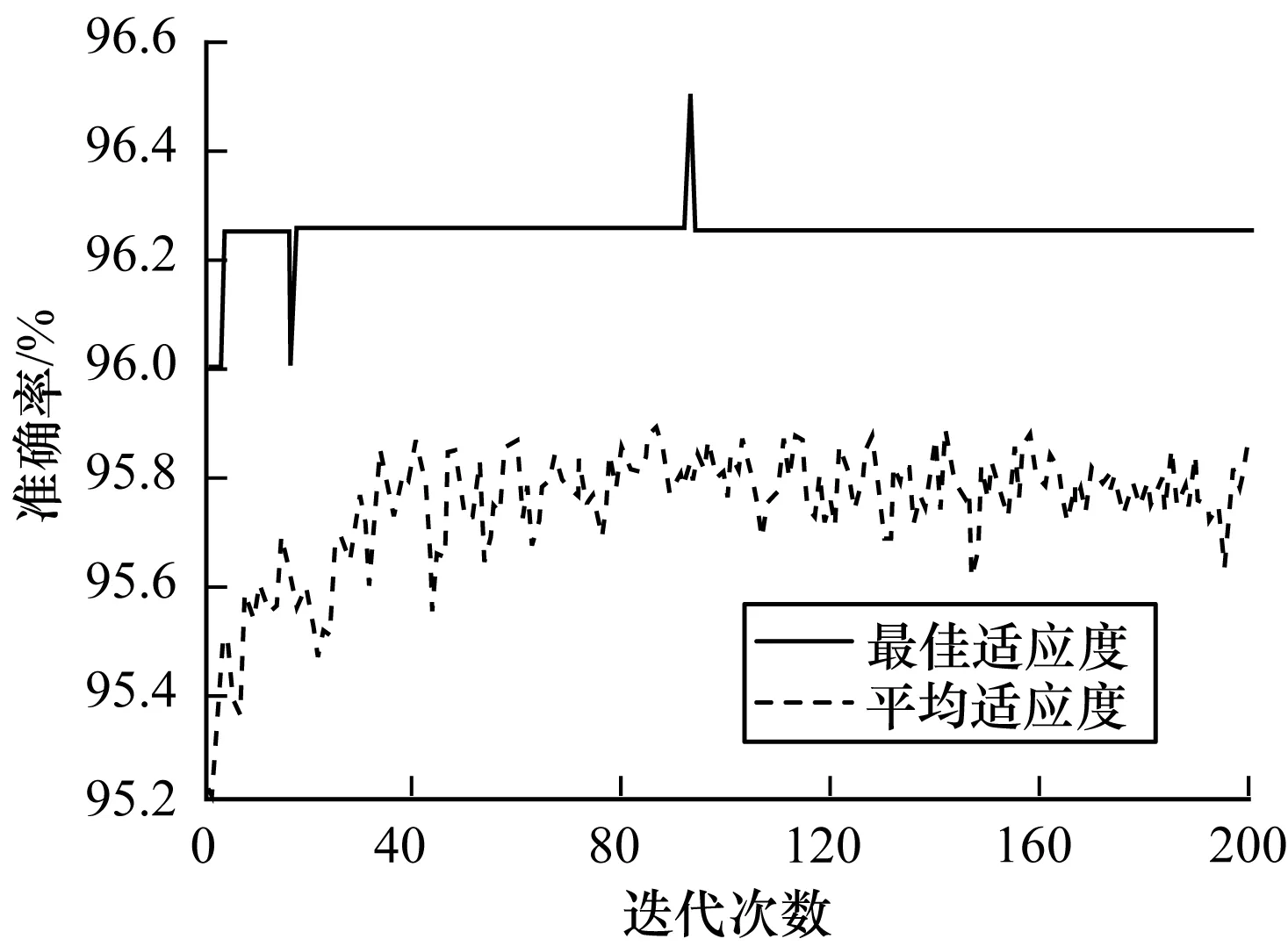
圖2 GA-SVM 算法參數優化過程曲線

從圖2可以看出,隨著迭代次數的增加,GA優化SVM模型的參數逐漸達到一個最佳適應度值,最后穩定在96.25%,此時的懲罰參數C與核函數參數g的組合達到SVM的性能最優,即最佳懲罰參數C=2.389,最佳核函數參數g=1.536。

4.2.5 與其他算法的性能對比

堆疊自編碼器是一種無監督的神經網絡模型,對高維采樣數據既能線性變換,又能表征非線性變

換。設定JNR的范圍為-12 dB,-10 dB,…,0 dB,在干噪比間隔為2 dB的條件下,本文設置了47-SAE-10-GA-SVM、47-Fisher-SFS-20-SVM、47-PCA-10-SVM、47-PCA-47-GA-SVM、47-KPCA-10-SVM、47-SVM 6種不同的分類模型,對比各模型在不同JNR條件下的平均識別性能、平均訓練時間與平均識別時間,具體測試的數據結果如表6所示。根據表6的仿真實驗結果可以得出如下結論:

1)冗余的特征信息不但不能夠幫助提高對雷達有源干擾信號的平均識別率,反而會大幅增加檢測模型計算的時間和復雜度,影響檢測模型對干擾信號類型的識別判斷。

2)基于特征降維的5種檢測模型(47-SAE-10-GA-SVM、47-Fisher-SFS-20-SVM、47-PCA-10-SVM、47-PCA-10-GA-SVM、47-KPCA-10-SVM)都能夠在保證平均識別率的前提下有效地進行特征降維,不同程度地去除了冗余信息,降低了運算的復雜度。其中,SAE-GA-SVM的分類算法憑借自編碼網絡的高效性能,取得了最優的識別率。

3)結合目前現代戰場復雜電磁環境的特點,對雷達有源干擾信號識別的關鍵是進行快速、準確地識別。相較于傳統的干擾檢測模型,基于SAE-GA-SVM模型對有源干擾的“平均識別時間”用時是最短的。雖然相較于傳統的檢測模型,其存在訓練時間較長的問題,但訓練時間是基于戰前的準備時間,不是關鍵因素。綜上所述,對于雷達新型有源干擾的識別,基于SAE-GA-SVM的模型是一種可行高效的干擾信號檢測模型。

5 結束語

本文針對雷達新型干擾的識別問題,提出一種基于SAE-GA-SVM的干擾檢測模型。結合分形理論與信息熵的思想,采用多域聯合的方法提取信號時域、頻域、小波域、雙譜域特征,分別運用6種分類模型進行性能對比,SAE依據神經網絡結構對高維數據進行非線性的數據降維與重構,實現最低的特征維度。仿真結果表明,相較于傳統的分類模型,SAE-GA-SVM具有較高的識別準確率。由于本文未考慮多種雷達干擾信號同時進入雷達接收機的情況以及沒有對采樣的數據進行去噪預處理,影響了模型的識別準確率,下一步將對此進行研究。