適用于電網異常負荷動態判別的CNN閾值模型

毛鈞毅,韓 松,李洪乾

(貴州大學 貴州大學電氣工程學院,貴陽 550025)

0 概述

隨著云計算、物聯網、移動互聯網等信息技術快速演進以及同步相量測量、廣域測量系統(Wide Area Measurement System,WAMS)的廣泛應用,電力數據呈現出高隨機、多耦合以及典型的“4V”等特征[1]。從數據驅動的角度出發,借助大數據技術與深度學習理論,有效挖掘和充分應用海量電網數據的信息,已成為現階段電力系統大數據建設的發展趨勢[2-4]。

隨機矩陣理論(Random Matrix Theory,RMT)是一種通過從高維角度理解復雜系統的行為特大數據分析方法。一方面,在基于RMT的電力系統分析理論與方法研究發展中,單環定律的平均譜半徑(Mean Spectral Radius,MSR)指標已在配電網運行狀態相關性分析[5]、電網薄弱環節辨識[6]以及電力系統不可見單元的檢測[7]等方面的應用取得初步成果。相較于MSR,基于M-P定律的樣本協方差矩陣最大特征值(Maximum Eigenvalue of Sample Covariance Matrix,MESCM)指標不僅能實現相同的應用,且更適用于低信噪比場景[8-9],在大規模電網中的計算效率更高[10]。然而,上述文獻對電網進行態勢評估大多在負荷波動較小的場景下開展,尚未對此類方法在具有周期性變化規律、波動性較大等特征的日負荷曲線動態電網中的適用性開展研究,如基于MESCM或MSR指標的閾值模型未能充分考慮數據波動性、靜態閾值對指標判定的可靠性偏低等。另一方面,近年來,卷積神經網絡(Convolutional Neural Network,CNN)[11]作為深度學習理論的模型之一,由于其強大的學習潛力以及優越的特征提取能力,已逐漸被引入到電力系統各個領域的研究中[12-15]。文獻[13]利用CNN對時頻譜進行特征提取,從而實現局部放電類型的識別。文獻[14]將CNN用于提取輸入信息特征,與強化學習相結合實現電網運行到控制策略的直接映射。文獻[15]依據CNN具有局部提特征獲取、權值區域及二次抽樣共享等特點,深入挖掘時間序列之間的相關特征,進而實現超短期風電的預測并取得較好的預測效果。

為研究基于數據驅動的電網態勢感知理論與方法,本文利用CNN模型進行負荷預測,從已確定電網的網絡構架以及相應機組的出力和開機方式角度使用預測負荷值,設定一種基于MESCM的動態閾值,進而提出適用于電網異常負荷動態判別的CNN閾值模型。

1 基于隨機矩陣理論的MESCM原理

1.1 考慮噪聲的PMU數據源矩陣的預處理

在廣域測量系統中,相量測量單元(Phasor Measurement Unit,PMU)能采集海量具有統一時間戳的狀態變量數據,如電壓和功角量測數據,使得電力系統的主控中心在每個采樣時刻均能采集到從各個PMU中上傳的狀態變量數據。將各個采樣時刻的數據按照時間順序排列,構成一個二維矩陣,即數據源矩陣XD,如式(1)所示:

(1)

由于傳輸過程中XD會受到隨機噪聲的干擾,則定義異常檢測模型為:

XD=XS+XmZ×ηZ

(2)

其中,XS為未受噪聲污染的信號矩陣,mZ為噪聲幅值,ηZ為噪聲矩陣[8]。

在得到受隨機噪聲所影響的數據源矩陣XD后,采用滑動窗口技術生成N×T維窗口數據矩陣X,根據M-P定律對矩陣X按式(3)逐行轉換為標準化的非Hermitian矩陣Xn:

Xn=(xi,j-μ(xi))×(σ(xni)/σ(xi))+μ(xni)

1≤i≤N,1≤j≤T

(3)

其中,xi=(xi,1,xi,2,…,xi,T)T,μ(xi)、σ2(xi)分別為行向量xi的均值和標準差,μ(xni)、σ(xni)分別為非Hermitian矩陣行向量xni的均值和標準差。

1.2 基于M-P定律的MESCM指標

隨機矩陣通常是一種高維以及各個元素獨立同分布的矩陣,RMT則是以此為研究對象,描述其特征值、奇異值以及相關參數的漸進行為的一種理論[16]。它主要涉及兩個定律,即M-P(Marchenko-Pastur)定律與單環定律,本文采用M-P定律,其原理描述如下:

設Xn={xi,j}1≤i≤Nz,1≤j≤T為一個N×T維的隨機矩陣,且每一個元素均獨立同分布。當均值μ(x)= 0、方差σ2(x)<∞時,Xn的樣本協方差矩陣S為:

(4)

(5)

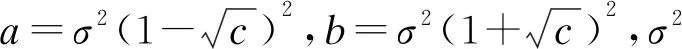
進一步地,若式(4)中Xn的各元素均為獨立同分布的變量,且均值為0、方差為1時,Xn的樣本協方差矩陣S的特征值分布收斂于M-P定律。本文以λmax表示樣本協方差矩陣S的最大特征值,即MESCM指標。

2 適用于異常負荷檢測的CNN閾值模型

2.1 CNN原理

CNN是一種適用于處理具有網格狀拓撲結構的數據的前饋人工神經網絡模型。典型的CNN由卷積層、池化層、全連接層構成,其層間結構如圖1所示。卷積層具有權值共享和局部連接的特點,能降低模型的復雜性,并減少過擬合的風險;而對于池化,其執行二次抽樣或局部平均,以降低輸出對數據波動的靈敏性,并提高模型的泛化能力。因此,與全連接神經網絡相比,CNN具有權值參數少、魯棒性好、泛化能力強與可并行學習等優點[17]。

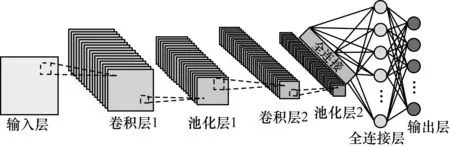
圖1 CNN網絡結構

2.2 CNN超短期負荷預測模型結構

超短期負荷預測是利用最新負荷信息,對未來5 min～1 h內的電力負荷進行實時預測,能夠在線跟蹤電力系統負荷變化,是動態電網安全監測的依據[18]。區別于圖像領域的二維CNN,本文采用一維CNN處理序列數據[19]其中模型的輸出向量yn+m(m=1,2,…,i)是n時刻后m個預測值,而輸入向量xn-k+1(k=1,2,…,j)是包括n時刻的k個歷史負荷數據值。由此,利用滑動窗口方法對時序歷史負荷數據逐一構建訓練樣本{xn-k+1,yn+m},從而完成對CNN負荷預測模型的訓練,并采用試錯法的方式確定輸入的歷史數據個數k值以提高預測精準度。

為更有效地提取歷史負荷的時序特征,本文建立一種兩層CNN模型,包括2個卷積層、2個平均池化層、1個全連接層、1個輸出層,以及在每個卷積層及全連接層后加入ReLU激活函數,如圖2所示,訓練時采用Adam算法進行參數優化。

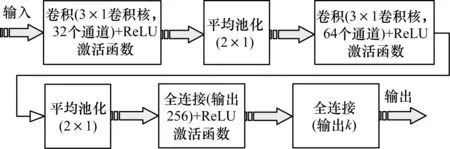
圖2 兩層CNN時序負荷預測模型結構

2.3 MESCM預測模型

因遭受噪聲、負荷波動性較大等因素的影響,電網運行過程實則是一個動態非平穩過程,對于由狀態變量數據計算出的MESCM指標在無異常發生時刻也是處于動態變化的。于是,為了有效地判定MESCM指標的非平穩趨勢,需要設定能夠響應MESCM指標變化的動態閾值。

考慮到電力負荷預測對保證動態電網的安全和可靠運行具有重要作用,利用CNN預測模型根據實時負荷數據求取出預測負荷值y,再通過已確定電網的網絡結構以及相應機組的出力和開機方式計算出電網未來的狀態變量數據矩陣XD,P;進一步地,計算出預測的樣本協方差矩陣SP的最大特征值λmax,P,從而設定MESCM指標的動態閾值并對電網運行狀態進行實時檢測。根據上述過程,定義基于CNN模型的動態閾值函數為:

(6)

其中,MESCM( · )為MESCM指標的計算模型,α(0≤α)為比例系數,可根據滑動窗寬度T進行調整[8],但隨機噪聲的強弱、窗口數據矩陣維度的大小以及CNN預測模型的精準度會對閾值模型的可靠性造成較大的影響。為此,結合異常擾動分級告警思路,該閾值考慮28%的裕度,選取α=1.28。當實時的MESCM指標越過閾值γ時,即λmax≥γ,則可判定電網有異常擾動事件發生。

此外,當上述動態閾值判定有異常擾動時,為了使基于預測負荷值的動態閾值不受異常擾動數據的影響,而導致誤判、漏判的現象發生,利用支持向量機對實時的擾動負荷數據進行預處理后再輸入到CNN模型中。支持向量回歸算法中的結構風險函數具有較好的平滑性,可以通過ε不敏感損失函數的作用來控制異常擾動數據對回歸模型的影響,從整體上考慮回歸曲線的平滑性,從而在負荷預測時減少異常擾動數據對CNN模型的干擾[20]。

3 本文方法步驟與流程

基于CNN閾值模型的電網異常負荷檢測的具體步驟如下:

步驟1獲取實時負荷數據,由訓練好的CNN模型進行負荷預測。

步驟2根據已確定電力系統,使用預測負荷值計算出電網未來的狀態變量數據,從而由式(1)構造預測的數據源矩陣XD,P。

步驟3由式(2)和式(3),對矩陣XD,P進行預處理,再結合式(4)獲得樣本協方差矩陣SP,計算并篩選出矩陣SP的最大特征值λmax,P。

步驟4根據矩陣SP的最大特征值λmax,P,由式(9)設定動態閾值γ。

步驟5獲取當前時刻的電網狀態變量數據,通過重復步驟3計算出實時S的最大特征值λmax,作為電網異常負荷檢測指標。

步驟6判斷λmax≥γ是否成立,若成立,則判定電網負荷出現異常擾動;否則重復步驟2～步驟6。

基于CNN模型的電網異常負荷檢測流程如圖3所示。

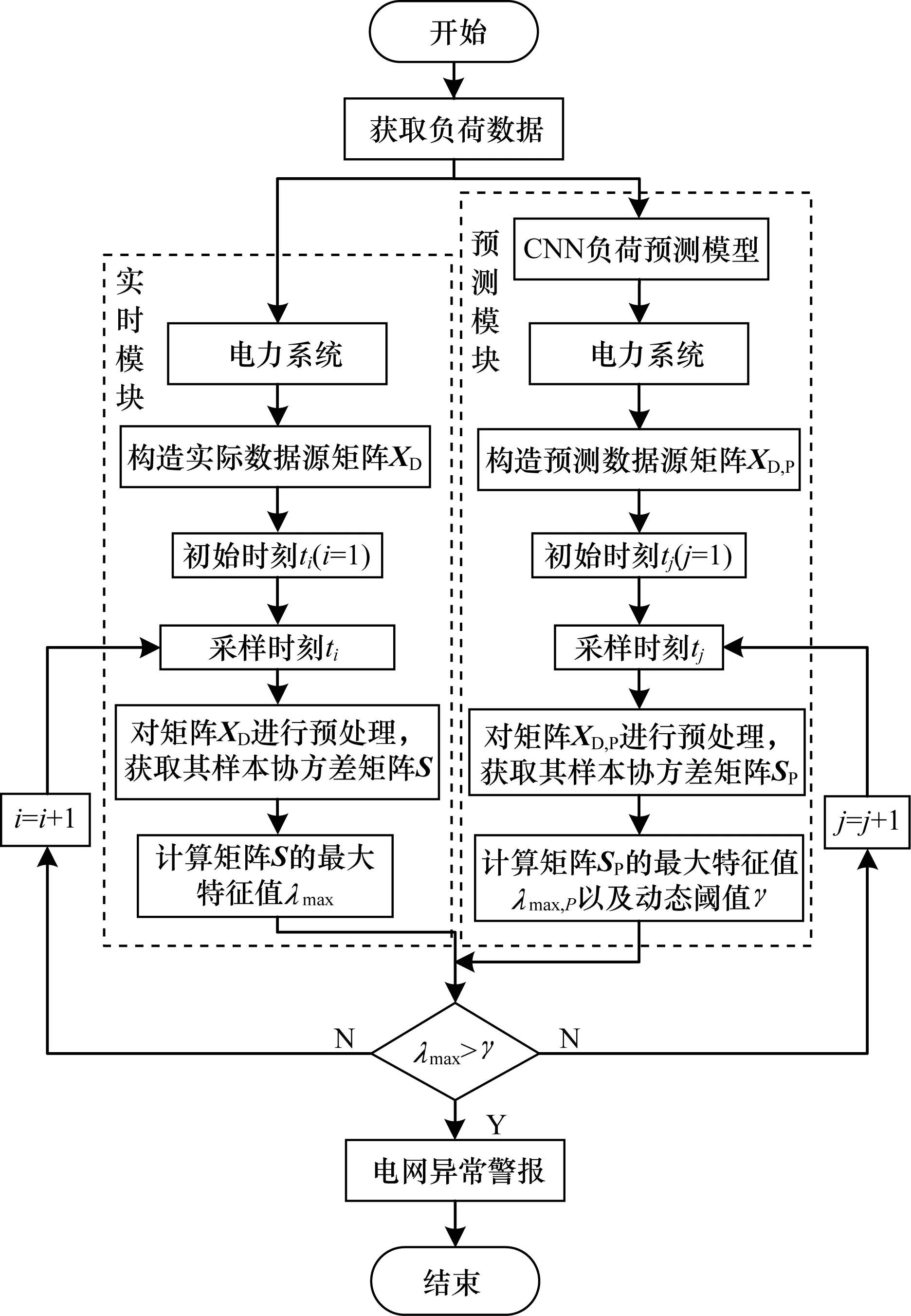
圖3 基于CNN模型的電網異常負荷檢測流程

4 算例分析

為驗證本文提出的適用于電網異常負荷動態判別的CNN閾值模型的有效性,以IEEE50機標準系統開展時域仿真獲取測試數據。一方面,對于CNN閾值模型,根據試錯法選取歷史負荷數據值k=14,再利用CNN模型預測未來5 min(m=5)的負荷值,從而計算出相應的預測閾值對MESCM指標進行實時監測;另一方面,借助Power System Toolbox (PST) Version 3.0工具軟件,以一個IEEE50機145母線系統[21]進行仿真測試,其中假設系統每個負荷節點有功負荷的變化規律與日負荷曲線相符,負荷采用1 440點日負荷形式,且通過三次樣條插值函數法[22]獲取每個0.15 min的負荷偽量測,進而模擬0.11 Hz[7]的采樣率。根據第3節方法步驟在Matlab R2014a軟件中編制算法程序,以驗證所提方法的有效性。

場景1負荷異常擾動測試。

為模擬實時測試中噪聲干擾,在該系統信號中引入高斯噪聲源,其中信噪比ρ=(40±0.3) dB,并設置系統中66號母線的負荷發生異常擾動變化,具體如表1所示。

表1 合成的異常負荷

按照第3節的步驟1和步驟2,利用CNN模型對獲取的負荷數據進行預測,從而通過IEEE50機145母線系統計算出預測負荷值對應的系統狀態變量數據,其中選取系統除平衡節點145外的其他144個節點的電壓幅值和發電機功角數據構成193維數據源矩陣進行分析。然后設置滑動窗口T=300,則維容比c=0.64∈(0,1],由步驟3分別計算出標準的非Hermitian矩陣、樣本協方差矩陣,進而根據步驟4設定MESCM指標的動態閾值。當采集到當前時刻的數據源矩陣時,通過步驟5,可以計算得到實時的MESCM指標。

按照時間序列依次對每個滑動窗口數據進行計算,可得出一天的MESCM指標以及對應的動態閾值曲線,同時,計算出文獻[8]所提出的Spiked閾值模型和式(5)中邊界閾值與本文所提出的CNN閾值模型進行對比,如圖4所示。

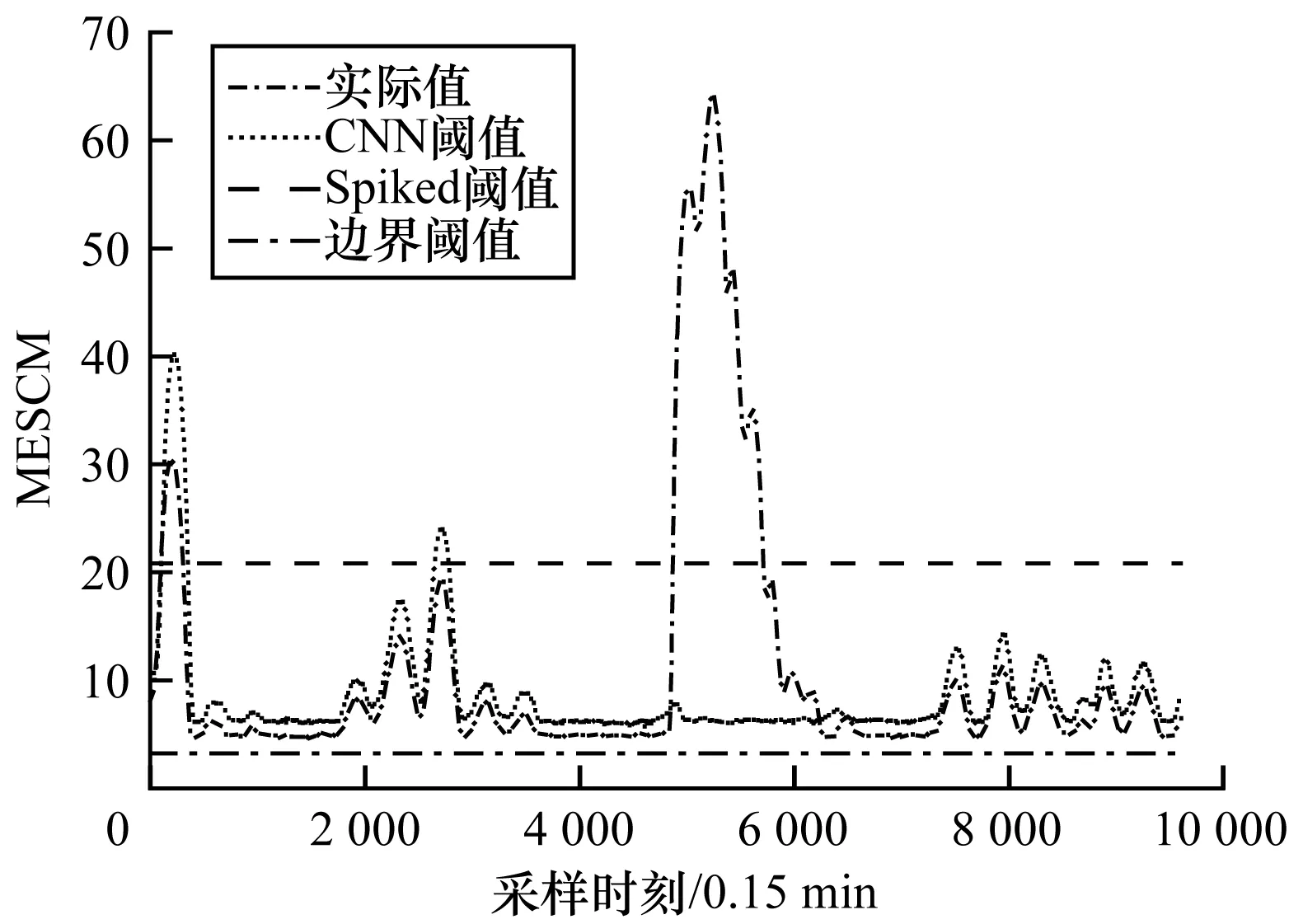
圖4 MESCM指標及閾值模型計算結果1

觀察圖4并結合表1可以發現,因在t4 801～t5 200采樣時刻內66號母線有功負荷突然增長100 MW,系統隨機性被打破,從而使得MESCM指標數值急劇增加,越過了CNN閾值以及Spiked閾值,說明這種閾值模型能夠有效判定MESCM指標的異常變化。而邊界閾值a僅與維容比c有關,且忽略了噪聲、負荷波動的影響,故未能有效地判定異常。然而,由于波動性負荷行為的影響,電網運行過程則是一個動態非平穩過程,因此MESCM指標或會在未發生異常階段出現急劇增長現象,如在t1～t400采樣時刻系統處于正常波動狀態并未設置異常擾動,但MESCM指標此時段內卻突然增大,明顯越過Spiked模型閾值,導致誤判現象的發生。而MESCM并未突破CNN閾值,表明該閾值模型在適應MESCM指標非異常的波動變化的同時,能夠判定出MESCM指標的異常擾動變化。

此外,將本文所提閾值模型應用于隨機矩陣理論的單環定律中,其中各參數與上述相同,但由于MESCM與MSR指標計算方式存在差異性,則在此設置式(6)中的比例系數α為0.98。根據大數據分析方法,可獲得MSR指標及各閾值的變化曲線,如圖5所示。

圖5 MSR指標及閾值模型計算結果

由圖5可知,在t4 801至～t5 200采樣時間段內隨著異常擾動的發生,特征分布出現“坍塌”現象,MSR指標跌落至最低值0.597 8,但并未偏離內徑限值,而在t4 801采樣時刻越過了CNN閾值模型,證明該閾值也能夠對MSR指標的異常變化進行有效判定。

場景2低信噪比場景下不同幅值異常擾動測試。

設置系統中66號母線的負荷異常擾動變化為表1的30%,并在ρ=(25±0.3) dB的低信噪比場景下進行測試,其他參數均與場景1相同,繼而根據第3節步驟可得到圖6。

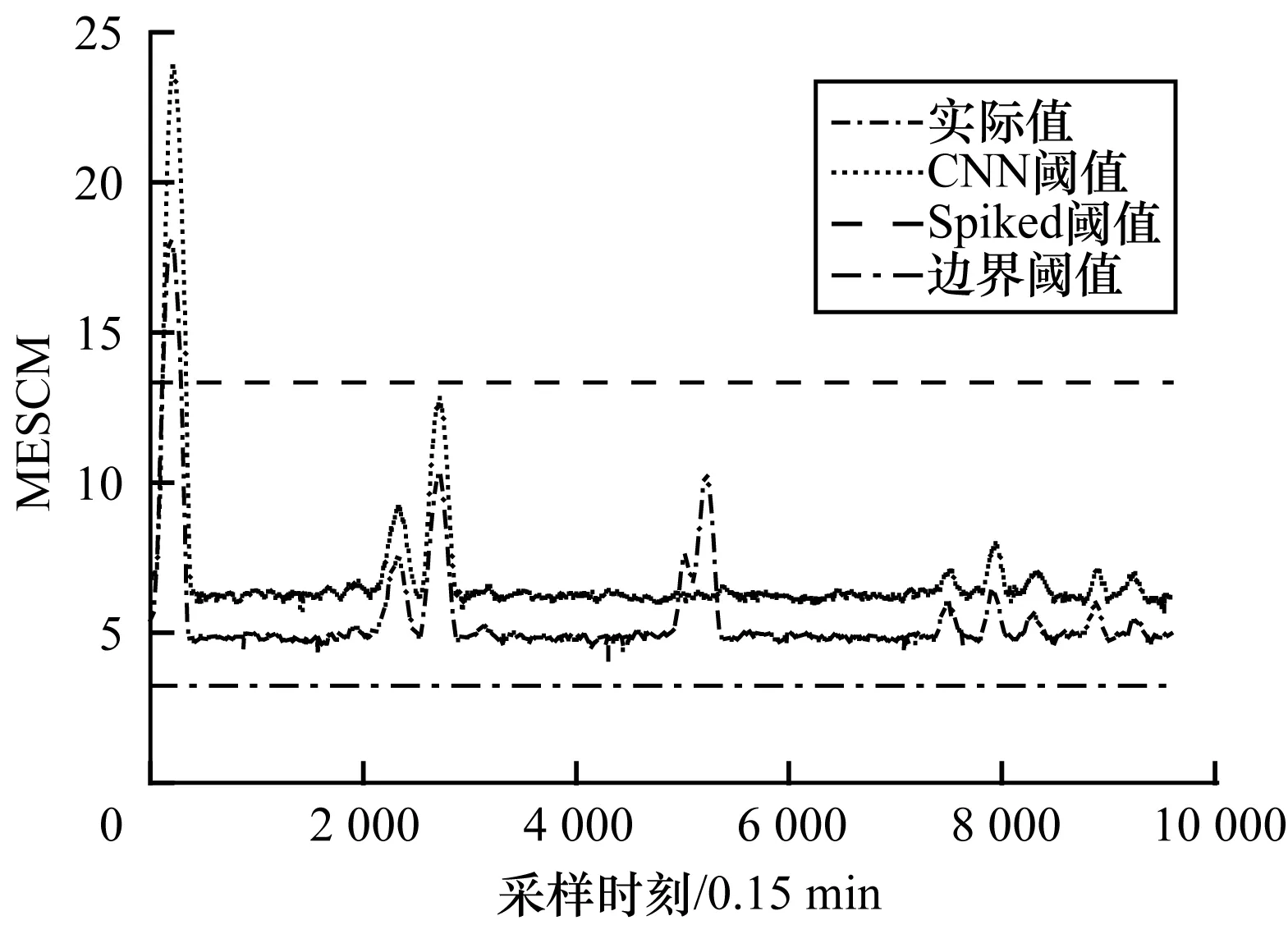
圖6 MESCM指標及閾值模型的計算結果2

對比圖4與圖6可知,在低信噪比場景下,由于強噪聲的影響以及異常負荷幅值的降低,圖6中的MESCM指標相比于圖4的MESCM指標整體降低了51%,同時,與信噪比ρ相關的Spiked閾值由20.8近似下降至13.3,但在t4 801～t5 200采樣時間段內MESCM指標并未越過Spiked模型閾值,從而導致了漏判現象的發生。此時,CNN閾值模型仍能判定出MESCM指標的異常變化,表明了基于CNN閾值模型的MESCM指標適用于低信噪比場景下不同幅值異常負荷的擾動判別。

5 結束語

本文提出一種適用于電網異常負荷動態判別的CNN閾值模型。基于MESCM方法與原理,利用CNN實現歷史負荷數據到動態閾值的映射,以及在負荷波動性較大的電網中MESCM對異常負荷的監測。借助Matlab R2014a和PST軟件工具,通過一個IEEE50機145母線標準系統的算例驗證了該方法的有效性,相較于傳統閾值模型,在動態電網中本文所提的閾值模型對MESCM指標的異常判定適應性更強,準確性更高。下一步將利用級聯CNN實現從電氣量測數據至閾值模型的直接映射,以提高對異常負荷識別的快速性。