導數法判斷函數零點問題的多種思維

◇ 山東 孟凡群

函數零點個數的判定是高考考查的重要內容,此類問題經常在解答題中出現,常用的解題思路是利用導數研究函數的單調性、極值、最值等,據此判斷函數圖象與x軸交點的個數．有時也需根據所給函數的類型將其分離為兩個簡單的函數,通過判斷兩函數圖象交點的個數來處理．

(1)當a<0時,求證:函數f(x)存在極小值;

(2)求函數f(x)的零點個數.

本文主要研究第(2)問，求解中將f(x)=xln (x+1)-ax2變形得f(x)=x[ln (x+1)-ax],易知x=0為函數的一個零點,其他零點可通過判斷g(x)=ln (x+1)-ax的零點得到,對于判斷函數g(x)零點個數的方法,本文給出如下三種．

1 直接判斷

通過利用導數研究函數的單調性、極值、最值等,結合函數的圖象與x軸的交點個數來判斷．

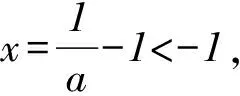
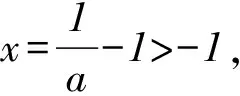
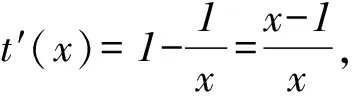
同理，a>1時,函數g(x)存在兩個零點,函數f(x)存在兩個零點．

綜上所述，當a≤0或a=1時,f(x)有一個零點;a>0且a≠1時,f(x)有兩個零點．

2 分離參數

對于含參函數的零點問題,若能將參數分離出來,則問題可轉化為平行于x軸的直線與確定函數圖象的交點問題．

解法2易知x=0為函數g(x)=ln (x+1)-ax的零點．

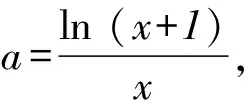
設t(x)=x-(x+1)ln (x+1),則t′(x)=1-[1+ln (x+1)]=-ln (x+1),在(-1,0)內,t′(x)>0,t(x)單調遞增;在(0,+∞)內,t′(x)<0,t(x)單調遞減,所以tmin(x)=t(0)=0,所以t(x)≤0,即h′(x)≤0,h(x)單調遞減．

圖1

綜上所述,當a≤0或a=1時,f(x)有一個零點;當a>0且a≠1時,f(x)有兩個零點．

3 分離函數

解法3由g(x)=ln (x+1)-ax=0，可得ln (x+1)=ax,則問題轉化為判斷C1:y=ln (x+1)與C2:y=ax的交點個數．

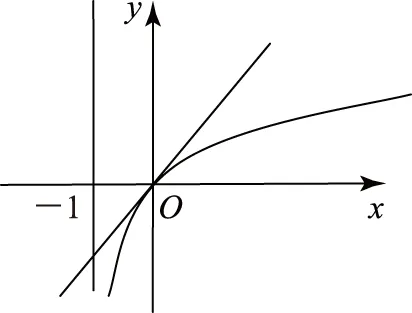
圖2

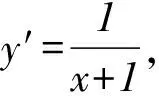
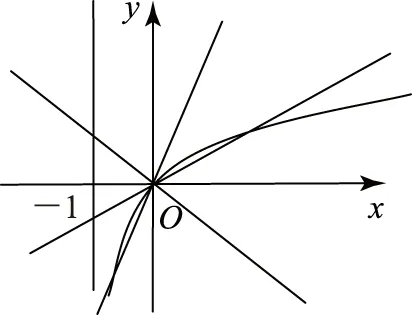
圖3

如圖3,當a>1或0

綜上所述，當a≤0或a=1時,f(x)有一個零點;當a>0且a≠1時,f(x)有兩個零點．