一種基于System Generator的CORDIC算法實現

胡天翔 陳科 趙志強

摘 ?要：在現場可編程門陣列（FPGA）芯片的應用中，選擇坐標旋轉數字計算（CORDIC）算法來實現正余弦函數的實時計算有著廣泛的應用。同時在信號處理領域上，對正余弦函數的計算有著高精度的需求。據此采用Simulink平臺的Xilinx公司開發工具System Genenrator（SysGen）設計了基于CORDIC算法實現正余弦函數計算的FPGA模型，將角度計算范圍擴展到全實數領域，并在理論上推導出該設計方案計算結果的誤差上限。仿真結果顯示，該設計方案的誤差精度與理論推導保持一致。而且，相比SysGen的系統自帶模塊，該設計可以避免重復嘗試，更好地控制計算精度。

關鍵詞：坐標旋轉數字計算機;現場可編程門陣列;正余弦函數;計算精度;System Generator

中圖分類號：TN911.72 ? ? ?文獻標志碼：A ? ? ? ? 文章編號：2095-2945（2020）19-0023-06

Abstract： In the application of field programmable gate array （FPGA） chip， choosing the Coordinate Rotation Digital Computer （CORDIC） algorithm to realize the real-time calculation of sine and cosine functions has a wide range of applications. At the same time， in the field of signal processing， there is a demand for high precision in the calculation of sine and cosine functions. Based on this， the FPGA model of sine and cosine function calculation based on CORDIC algorithm is designed by using System Genenrator （SysGen）， a development tool of Xilinx company on Simulink platform， which extends the range of angle calculation to the field of all real numbers， and deduces the upper limit of error of the calculation result of the design scheme in theory. The simulation results show that the error accuracy of the design scheme is consistent with the theoretical derivation. Moreover， compared with the system with its own module of SysGen， this design can avoid repeated attempts and better control the calculation accuracy.

Keywords： coordinate rotation digital computer; field programmable gate array; sine and cosine functions; calculation accuracy; System Generator

引言

在AI、自動駕駛及物聯網等信息技術蓬勃發展的今天，數據處理的高精度實時性需求越發被人們所重視。在現場可編程門陣列（FPGA）出現伊始，業界就有一種觀點認為FPGA可以被用來加速計算（computing）的過程。現今FPGA更是已經成為數字信號處理系統的核心器件，其高速并行能力使得它成為高性能數字信號處理的理想平臺[1]。

傳統的FPGA設計流程，需要從算法設計階段的高層次計算機語言（如C++）轉換到硬件實現階段的底層HDL語言（如Verilog），這個過程的時間成本很高，而且易產生一些錯誤[2]。MATLAB中的Simulink給復雜的DSP算法的硬件化提供了一個很便利的開發平臺，在該平臺上，利用Xilinx公司的開發工具System Generator（SysGen）不僅可以快速準確的實現硬件的建模與仿真，而且可以將抽象的模塊化電路圖直接轉化為硬件描述語言，并生成測試文件，可以有效縮短開發周期[3]。

傳統的CORDIC（Coordinate Rotation Digital Computer）算法在圓周坐標系統下的的收斂范圍在[-99.82°，99.82°]，并沒有覆蓋到任意角度[4]。且CORDIC算法具有迭代性，迭代次數和定點數運算中數據位寬的選擇都直接關聯到計算結果的精度。增加迭代次數和數據位寬都會帶來硬件資源占用的影響，同時反復進行迭代也會使得運算速度變慢。這樣在滿足工程上精度需求的前提下，合適地選擇迭代次數和數據位寬可以在節省硬件資源成本和響應速度上得到很好的兼顧。

針對上述問題，為避免設計時的不斷重復嘗試。本文在Simulink平臺上針對圓周系統下CORDIC算法設計了正弦余弦函數的計算模塊，將可計算的范圍擴展到任意角度，并在理論上給出了該設計的誤差上限。根據本文給出的誤差上限分析，適當選取迭代次數和數據路徑中的小數位數，可以同時兼顧計算速度和硬件消耗，更高效地實現定點數的正余弦函數計算。

1 CORDIC算法基本原理

CORDIC算法由J.Voider等人于1959年在航空控制系統的設計中提出來[4]。這種算法應用于硬件平臺上，只要執行移位和加法運算，就能實現一些復雜的超越函數（如三角函數）。該算法在數字信號處理領域得到了廣泛的應用。其算法原理如下[5]。

在CORDIC算法圓周坐標系旋轉中，給定的初始向量{x（0），y（0）}，起始角度z（0）。第i次迭代旋轉如圖1所示。

3 基于System Generator的CORDIC正余弦計算模塊設計

FPGA廠商Xilinx公司在Simulink平臺上提供了System Generator開發工具，用戶可以基于此工具高效建模，在FPGA上實現DSP算法。還可以自動生成HDL代碼和測試文件，將模型直接轉化為ISE工程，大大提高了設計效率[7]，是數字信號處理系統設計與Xilinx公司FPGA實現的“橋梁”。而且在SysGen環境下，采用基于模型的設計方法可以方便地實現和驗證定點算法，發現問題后也容易進行修改[8]。

3.1 模塊設計方案

本次模塊針對正弦和余弦計算，采用的是CORDIC算法圓周坐標系下的旋轉模式。設置初始向量為？淄（0）=（1/Kn，0）'，同時z（0）為我們要求解的目標角度。經過n次迭代后迭代累計角度z（n）趨近于0，也就意味著向量旋轉趨近于目標角度。此時的向量模長增益趨近于1，向量的x坐標趨近于cosz（0），y坐標趨近于sinz（0），據此可計算z（0）的正弦值和余弦值。

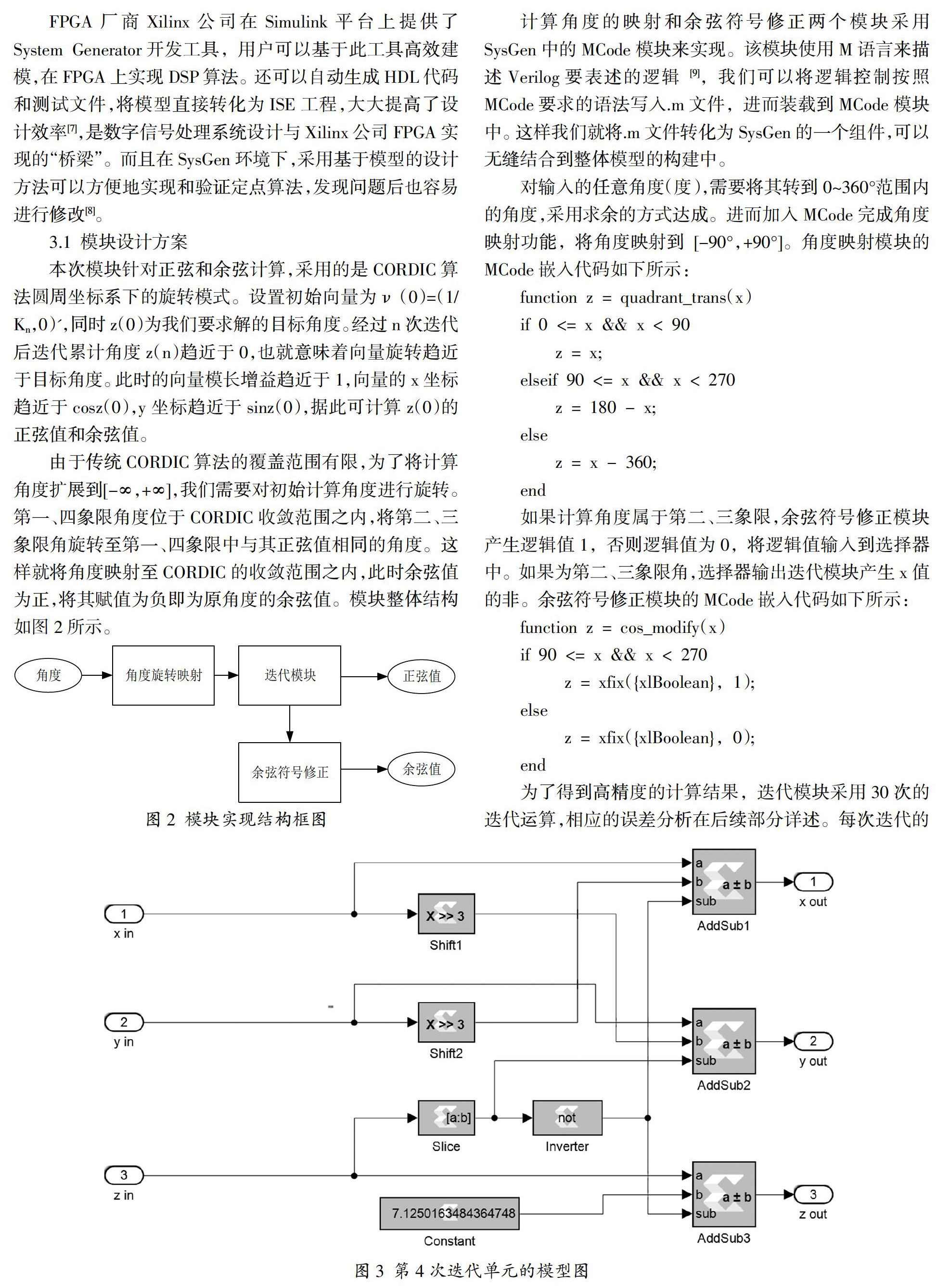
由于傳統CORDIC算法的覆蓋范圍有限，為了將計算角度擴展到[-∞，+∞]，我們需要對初始計算角度進行旋轉。第一、四象限角度位于CORDIC收斂范圍之內，將第二、三象限角旋轉至第一、四象限中與其正弦值相同的角度。這樣就將角度映射至CORDIC的收斂范圍之內，此時余弦值為正，將其賦值為負即為原角度的余弦值。模塊整體結構如圖2所示。

計算角度的映射和余弦符號修正兩個模塊采用SysGen中的MCode模塊來實現。該模塊使用M語言來描述Verilog要表述的邏輯[9]，我們可以將邏輯控制按照MCode要求的語法寫入.m文件，進而裝載到MCode模塊中。這樣我們就將.m文件轉化為SysGen的一個組件，可以無縫結合到整體模型的構建中。

對輸入的任意角度（度），需要將其轉到0～360°范圍內的角度，采用求余的方式達成。進而加入MCode完成角度映射功能，將角度映射到[-90°，+90°]。角度映射模塊的MCode嵌入代碼如下所示：

function z = quadrant_trans（x）

if 0 <= x && x < 90

z = x;

elseif 90 <= x && x < 270

z = 180 - x;

else

z = x - 360;

end

如果計算角度屬于第二、三象限，余弦符號修正模塊產生邏輯值1，否則邏輯值為0，將邏輯值輸入到選擇器中。如果為第二、三象限角，選擇器輸出迭代模塊產生x值的非。余弦符號修正模塊的MCode嵌入代碼如下所示：

function z = cos_modify（x）

if 90 <= x && x < 270

z = xfix（{xlBoolean}， 1）;

else

z = xfix（{xlBoolean}， 0）;

end

系統整體模型如圖4所示，如前所述，輸入常量x為1/K（30），K（30）為偽旋轉30次迭代后所產生的增量倍數，輸入常量y為0。Mod_function為取余運算模塊，將全范圍的角度轉到[0°，+360°]范圍內。經30次迭代運算后，輸出y為正弦值，輸出x經多路選擇器輸出后為余弦值。

3.2 模塊整體誤差分析

4 仿真結果與分析

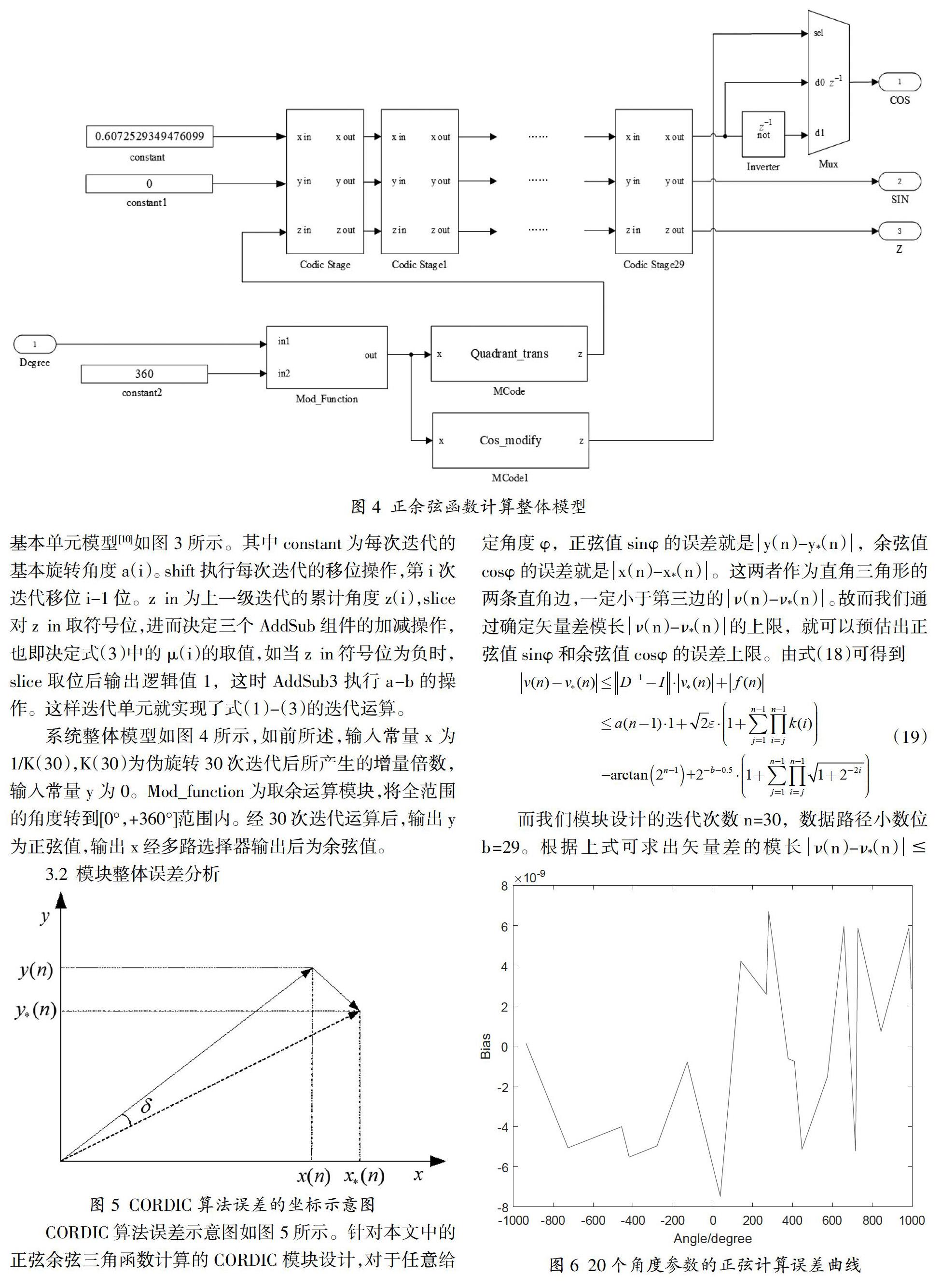
在[-1000°，1000°]內隨機生成20個角度值帶入設計的模塊中做正弦值計算。將所計算的結果與MATLAB代碼計算的結果做差求得誤差集合。以橫坐標為角度（以度為單位），縱坐標為誤差值作圖，正弦計算誤差曲線如圖6所示，余弦計算誤差曲線如圖7所示。

從以上兩圖可以看到，隨機生成的角度經設計模塊運算后的的正余弦值計算結果誤差均未超過4.1665×10-8，與我們理論分析的結果是一致的。

將System Generator自帶模塊，設置同樣的迭代次數和位數，對20個隨機生成的角度進行求解，所得結果與MATLAB計算結果的誤差曲線圖如圖8所示。本文所設計的正余弦函數計算模塊的精度要優于系統自帶模塊。