語法與語義接口理論的兩條進路

陳鵬

語言伴隨人類已經有數萬年以上的歷史了，然而人類對語言本質的了解還很初步。僅僅是在19 世紀，語言學還只不過是文獻學或者人類學的一個分支，直到20 世紀，語言學才真正成為一門科學。

當學習一門語言的時候，我們通常會區分兩部分的知識：一部分是詞匯知識，另一部分是一般的語法知識。這種區分中似乎將詞匯和句法進行了一個二分。

1 句法本位和詞匯本位

也許，語言最為重要的一個秘密就隱藏在著名德國語言學家洪堡（W.von Humboldt）的論述中：“語言面對的是一個無窮無盡且真正無界限的領域，面對的是能被思考的萬物本質。因此，它必須無限地使用有限方法，并通過產生語言和思想的標識能力來實現。”（[8],第91 頁）對于洪堡的這段表述，后人一般都將其簡述并抽象為對語言本質的一句概括，即：“語言是‘有限方法的無窮應用’”（language is the‘infinite use of finite means’）。語言中的語句集合顯然是無窮的1當然，究竟語句集合是哪一類無窮？是可枚舉的嗎？這些問題都還存在爭論。，然而生成語句的方法是有限的，幾乎我們每一個人都能掌握這些有限的方法。要想研究語言，從這些有限的方法入手進行研究是比較有效的途徑。

根據所理解的“有限方法（finite means）”的不同，語言學理論大致可以分野為句法主義和詞匯主義。相較而言，句法主義（syntacticism）聚焦句法，更加側重在短語結構構成的語法規則上。在句法主義的視域下，“有限方法”就是句法規則，喬姆斯基（N.Chomsky）用遞歸的形式文法體系揭示出“有限方法的無窮應用”的本質。相較而言，從詞匯主義的立場來看，“有限方法”其實就是蘊藏于自然語言的“有限詞匯”中，詞匯主義（lexicalism）認為組合詞匯的語法系統與組合短語的語法系統是獨立的，語法信息根植于語言的詞匯。產生詞匯的組合系統應該與產生短語的組合系統應該具有不同的原則。正如蘭貝克（J.Lambek）所言（[10]）：“一個被形式化的語言句子結構完全是由它的類型列表所決定的。”

句法主義的核心代表是喬姆斯基的轉換生成語法，而詞匯主義的發展相對分支較多，包括中心語驅動的短語結構語法（HSPG）、詞匯功能語法（LFG）與組合范疇語法（CCG）等。

1.1 喬姆斯基的句法結構

喬姆斯基在《語言描寫的三個模型》（[1]）、《句法結構》（[4]）、《有限狀態語言》（[5]）、《論語法的某些形式特性》（[2]）和《語法的形式特性》（[3]）等系列論文和著作中，建立了形式語言理論的完整系統。

喬姆斯基在[2]中將形式文法描述為一個系統G，它是一個以有限符號集合V為其元素，以I為其單位元素集合的字符串接的半群，可記作：

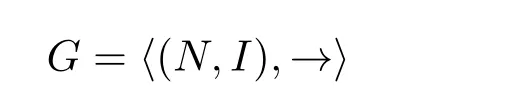
其中，V=VT ∪VN，VT表示終結符，VN表示非終結符（包含邊界元素“#”），且VT與VN不相交。

→是在G上定義的一個二價關系，讀作“可重寫為”。該關系滿足下面四個條件：

公理1→是非自反的；

公理2A ∈VN，當且僅當存在φ,ψ,ω，使得φAψ →φωψ；

公理3 不存在φ,ψ,ω，使得φ →ψ#ω；

公理4 存在有限偶對集合(χ1,ω1),...,(χn,ωn)，使得對于所有φ,ψ，φ →ψ

當且僅當存在φ1,φ2，且j ≤n，使得φ=φ1χφ2且ψ=φ1χφ2。

當實施以下約束后：

約束1 如果φ →ψ，那么存在A,φ1,φ2,ω，使得φ=φ1Aφ2,ψ=φ1ωφ2，且；

約束2 如果φ →ψ，那么存在A,φ1,φ2,ω，使得φ=φ1Aφ2，ψ=φ1ωφ2，且，但A →ω；

約束3 如果φ →ψ，那么存在A,φ1,φ2,ω,a,B，使得φ=φ1Aφ2，ψ=φ1ωφ2，且，A →ω，但ω=aB或者ω=a。

約束1 要求文法規則形如φ1Aφ2→φ1ωφ2，其中A是單個符號，。

約束2 要求文法規則形如A →ω，每個規則都可以獨立于A出現的上下文。

約束3 要求文法規則限定在A →aB或者A →a，其中A和B是單個非終止符，a是單個終止符。

基于上述的形式化描述，喬姆斯基將語言的結構形式定義為四種類型。分別對應上述約束i，形成i型文法。即：滿足約束1 的為1 型文法；滿足約束2 的為2 型文法；滿足約束3 的為3 型文法，此外沒有約束的文法為0 型文法。相應的文法以及對應的語言、自動機參見表1。

表1:喬姆斯基的形式文法

在喬姆斯基的形式文法之后，語言的結構便可以按照不同的文法遞歸生成對應的不同的語言。這樣的話，語言便形成一種螺紋狀的層次結構，如圖1 所示。

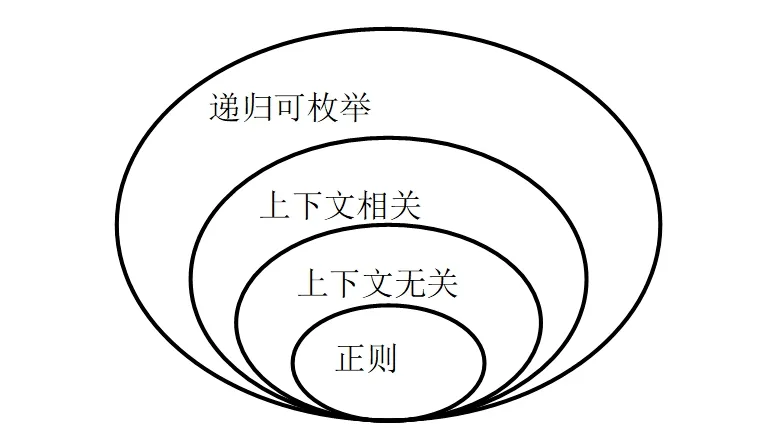
圖1:基于喬姆斯基形式文法的語言層次結構

喬姆斯基眼中的語言世界是非常簡潔而美好的，通過極其簡練的幾個句法規則，就可以產生如此豐富、美妙的語言。

1.2 組合范疇語法

與喬姆斯基的句法結構所不同，詞匯主義的發展以詞匯的形式化為核心，我們以組合范疇語法為例，展示詞匯主義的核心思路。斯蒂德曼（M.Steedman）使用基于組合邏輯（[6]）的組合子規則的擴充古典范疇語法，創立了原生態CCG，旨在解決自然語言中大量存在卻在上下文無關語法中不太容易得到解決的現象，如賓語提取、非外圍抽象、詞序靈活性、重成分NP–移位、動詞毗連、主目毗連、直接成分的非連續性現象和多動詞句、無界依存和寄生語缺（parastic gapping）等涉及到有界或者無界依存關系的自然語言表達式結構（[12,13]）。

CCG 主要由范疇和組合規則兩部分構成。其中所有的詞都指派一個對應的范疇，而范疇指的是它能夠和什么樣的論元組合以及與該論元組合之后會生成什么范疇，換言之，就是它的函數類型。詞匯便成了從詞匯條目到范疇的映射，意味著每個詞匯條目尋求論元的行為。

范疇的集合是由一個原子范疇集合組合而成的：

定義1.給定一個有限的原子范疇類F，集合C是滿足下列條件的最小集合：

a)F ∈C

b) 如果X,Y ∈C，那么X/Y,XY ∈C

例如，如果F={S,NP}，那么C的元素例中包括原子S和原子NP，以及(SNP) 和(NPNP)(NPNP)。由原子不斷遞歸生成的對象被稱為函子或復合范疇。

在任何一種復合范疇X/Y或XY中，我們將Y稱為論元范疇，X為結果范疇；對任何X類來說，其修飾范疇的形式為X/X或XX，被修飾成分不做變化。在漢語中，詞類如形容詞和副詞擁有修飾功能，這是因為形容詞和副詞分別修飾名詞和動詞，如：

(1) a.法規性?NP/NP；

b.然后?(SNP)/(SNP);

范疇聲明它們的論元獲取行為（argument-seeking），而組合規則作用于范疇之上使兩個范疇依據其規定形成新的范疇。

組合規則給多個標記（token）賦予主要類型（principled types），并基于輸入符號的范疇來限制組合的類型。由于組合規則與柯里（Curry）等（[6]）的組合子（combinators）之間緊密相關（close relationship），每個組合規則都有一個語義解釋，這在語法分析過程中，允許語法派生同時構建謂詞–論元結構（predicate-argument structure）。

表2:CCG 中范疇與語義規則

例(2)展現在組合范疇語法視域下，一個典型漢語語句的語句生成過程與范疇演算過程。

(2) 甘肅省積極探索高風險業務

此外，CCG 直觀地體現了意義組合原則，其規則中語法與語義嚴格對應。CCG通常可以實現句法與語義并行推演，如例(3)所示。

(3) 張三吃了飯

2 語法與語義界面問題的源流與發展

語法與語義界面的問題與對語言結構的認識有著緊密的關系。在早期，人類對自然語言的理解是一體的，并不很嚴格地區分語法與語義。伴隨著人類對語言的不斷理解，語法與語義之間的界面不斷顯露且清晰。在喬姆斯基提出句法結構之前，語法與語義界面的問題并沒有顯露出來，也并沒有作為一個嚴肅的科學主題受到過關注。在喬姆斯基的句法結構革命之后，語法與語義界面如同冰山一般逐漸露出了海平面。

喬姆斯基的《句法結構》之后，通過形式語法工具，將散落在盤子中的語言珍珠用形式語法這根金線串起來。通過語法的表層結構和深層結構的劃分，似乎人類找到了理解語言的鑰匙。基于轉換生成語法，通過將否定和疑問語素加入到深層結構中，卡茨（J.Katz）和福多（J.Fodor）認為只需要通過深層結構便可以確定句子的意義。在1965年左右，人們普遍對卡茨–珀斯特假說持有樂觀的態度，所謂的卡茨–珀斯特假說是“所有的轉換都是意義保持的（meaning preserving）”（[9]，第23 頁）。

卡茨–珀斯特假說讓人類對語言的理解進入一個伊甸園時期，用簡潔而美的句法形式就能勾畫出如此豐富美妙的自然語言，無論是其形式或者其意義都完全在人類的掌握之中。

然而，很快地，量詞轄域歧義問題就暴露出轉換生成與語義之間的問題，并擊破了卡茨–珀斯特假說。這里所謂的量詞轄域歧義問題涵蓋反身代詞、等名消除（Equi-NP Deletion）和并列縮略（Conjunction Reduction）等不同情形，具體如例(4)至例(9)所示。

(4) a.張三投了自己一票。

b.張三投了張三一票。

(5) a.每個人都投了自己一票。

b.每個人都投了每個人一票。

例(4)表明反身代詞的轉換規則在應用到專名（“張三”）的情況下是意義保持的，然而當應用到例(5)量化名詞短語（“每個人”）的時候卻并不是意義保持的。

(6) a.張三想要獲勝。

b.張三想要張三獲勝。

(7) a.每個人都想要獲勝。

b.每個人都想要每個人獲勝。

例(6)表明對于專名而言，等名消除的轉換規則應用后，意義保持不變，然而在例(7)中等名消除的轉換規則應用到量化名詞短語時意義卻發生變化。

(8) a.3 既是偶數又是奇數。

b.3 是偶數，并且3 是奇數。

(9) a.沒有數既是偶數又是奇數。

b.沒有數是偶數，并且沒有數是奇數。

例(8)和例(9)同樣都是并列縮略的轉換規則，但作用對于專名和量化名詞短語所表現出來的意義保持卻不相同。例(8)在并列縮略的轉換規則下是意義保持的，而例(9)在并列縮略的轉換規則下意義卻發生變化。

例(4)至例(9)所展現的問題核心是轉換生成與語義之間的問題，語義的問題已經不能完全由深層結構所確定。這個時候，原本在卡茨–珀斯特假說中明晰的語法–語義界面又變得模糊起來了。由于這個問題，引發了語言學史上著名的一場語言學戰爭（[7]），其中一派是生成語義學派，另一派是解釋語義學派。戰爭的結果并不是一派戰勝另一派，而只是將人類從由卡茨–珀斯特假說所構筑的語言伊甸園中驅逐出來。人類又一次被語法與語義之間模糊而難以琢磨的關系所困擾。

蒙太格語法使得人類又一次重新認識語言，相比于喬姆斯基的句法結構革命，這一次的認識轉向對語義有了一個全新的認知。蒙太格提出語法實際上是一種“形式”的代數，語義是一種“意義”的代數，且在句法代數和語義代數之間存在著一種同構關系。這種語言觀重塑了語法與語義的界面。

此外，蒙太格語法對與語法與語義界面研究的最主要的貢獻是技術層面的。蒙太格語法對于語法與語義的界面提供了兩個至關重要的技術工具，一是Lambda 演算，另一是將內涵視為弗雷格的高階函項。

在蒙太格語法之前，通常采用一階邏輯來描述自然語言。然而，一階邏輯的表達能力與自然語言相比實在是差距甚遠。通常，我們使用一階邏輯與自然語言的照應如表3 所示。一階邏輯通常主要能夠刻畫一般的動詞、通用名詞、形容詞、專名等，然而對于限定詞、量詞、介詞、副詞以及相關的一些短語，一階邏輯都不能很好地進行刻畫。

然而，當有了Lambda 演算和高階函項，刻畫自然語言的方法豐富了很多。Lambda 演算為函項表示提供了重要的基礎，在以往的函項中，有一些復雜語句是不能給出其組合語義的。

通過Lambda 演算，可以在不依賴于論元的前提下，提供指稱函項的一種方法，因此可用于為類似量化限定詞設計合理的語義。以例(7)為例，我們可將“每個”翻譯為一個二階函項，并通過與“人”這個通用名詞組合產生廣義量詞指稱。Lambda 演算為分析復雜表達式的意義提供了方法，明確了一個從自然語言語法到語義翻譯的組合式過程，為語法樹的每一個節點都指派一個合適的意義。

(10) 每個人都在讀書

蒙太格語法無疑是里程碑式的，其影響也極為深遠。實際上，蒙太格語法并沒有完全地實現蒙太格為形式語言和自然語言構筑一個通用文法的夢想，然而它卻對邏輯學，尤其是數理邏輯和語言學的融合起到了奠基性的作用。2在蒙太格語法之后，國際上逐步形成了一門名為“形式語義學”的邏輯與語言的交叉學科。對于語法與語義界面的問題，蒙太格語法也并沒有給出最終的答案，然而它將語法和語義分別視為兩個自治的系統，且彼此存在著緊密關聯（同構）的這一觀點為后人對待語法與語義提供了非常關鍵的啟示。雖然語法與語義界面的問題猶如荊棘一般，仍布滿在人類通往語言理解的路途中，然而人類手上已經持有數理邏輯的利刃，一路披荊斬棘。

在蒙太格語法之后，如果我們認為語法和語義都是自洽的，那么語法與語義的界面問題突出地表現在語法與語義的不匹配。而語法與語義的界面理論本質上都是對這些不匹配的消解方法。比較常見的語法與語義界面的現象包括：論元識別、量化、歧義等。

(i)論元識別問題

在一般情形下，在語態和邏輯語義詞匯之間存在一個非常清晰的照應：我們可以將一個專有名詞翻譯或者解釋為一個個體，將帶有一個主體和n個補語的動詞翻譯或者解釋為帶有n+1 個論元的謂詞。例如：

(11) a.張三喜歡王芳。

b.喜歡(張三,王芳)

句法結構與語義結構非常不同。即使我們能夠標識出詞與其意義之間的映射，我們知道整個語句的真值條件，我們仍然沒有謂詞–邏輯公式的子表達式，照應動詞短語節點的意義。語法與語義的界面需要確保直接賓語的指稱與謂詞“喜歡”的第二個語義論元槽關聯，同時主語指稱必須與第一個論元槽相關聯。

論元標識的另一個問題是當謂詞的語義元并不對應句法價。例如：

(12) a.張三看上去很疲憊。

b.看上去(很疲憊(張三))

從表層而言，張三是看上去的主語，然而張三又不是謂詞看上去的語義論元。

(ii)量化問題

一般情形下，動詞的句法依存成分被翻譯為動詞的語義論元。然而，當依存成分是量化的，例如：

(13) 每個人都在讀書。

a.For all(reading)

b.?x[man(x)→reading(x)]

其中，動詞的翻譯被視為主語的語義論元。因此我們可以假設“每個人”翻譯為高階謂詞For all，它將一個一階謂詞“reading”作為其論元。在(10b)這個標準的謂詞邏輯翻譯中，主語的語義貢獻分散在整個表達式中。然而，主語的一部分被視為“reading”的論元，同時reading(x)這一公式卻處于量化詞?的轄域中。

(iii)轄域歧義

在自然語言中，歧義現象是比較普遍的。我們以轄域歧義為例：

(14) 每個學生都在編寫某個程序。

a.?x(λx.student(x)→?y(λy.(program(y)∧wrote(x,y)))

b.?x(λx.program(x)∧?y(λy.student(y)→wrote(y,x)))

例(14)是一個非常典型的量詞轄域問題。對于同樣一句話，由于量詞所采用的轄域寬窄不同就產生了不同的解讀。(11a)中“每個學生”中的“每個”采取了寬轄域，而“某個程序”中的“某個”處于“每個”的轄域范圍內。這樣的解讀表明每個學生可能都在編寫完全不同的程序。(11b)中“某個程序”中的“某個”采取了寬轄域，而“每個學生”中的“每個”處于“某個”的轄域范圍內。這樣的解讀表明所有學生都在編寫同一個程序（比方說求100 的階乘）。

量詞轄域歧義問題是語法與語義界面中普遍存在的一個重要現象，我們還可以列舉一些相關的例子。

(15) a.大多數語言學家會講兩種語言。

b.所有男生都喜歡某個籃球運動員。

c.所有程序員都會用一種程序語言進行編程。

3 語法與語義界面的兩條進路

任何的語法與語義界面理論都是一種將語法分析與語義分析關聯的理論。在喬姆斯基和蒙太格的工作后，對于語法與語義界面的研究蓬勃發展。然而，總體而言，在語法與語義界面的理論有兩條比較主要的進路，一條是以詞匯為中心的詞匯主義路線，另一條是以句法為中心的句法主義路線。

詞匯主義路線的代表是范疇語法，最初的范疇語法可以追溯到AB 演算，在蘭貝克那里得到比較完善的形式化描述。莫特蓋特（M.Moortgat）對范疇語法的語法與語義界面觀做過總結：

范疇類型邏輯對于形式與語義之間的關系給出一個高度透明的觀點：語義解釋能夠直接通過證明獲取，同時證明也構建了表達式的良型（可生成）。組合性原則以一種特別嚴格、純粹演繹的形式實現，沒有為規則到規則所規定的意義指派遺留任何空間。（[11]，第115 頁）

句法主義路線的代表是喬姆斯基學派的轉換生成語法以及邏輯形式（Logic Form，簡稱“LF”）。在LF 方法中，句法被視為句法表征集合，從D結構出發，被映射為S結構，然后再被同時映射為音素形式（Phonological Form）和LF。這些表征是句法樹。這種語法–語義界面觀點給我們提供一個明確的界面層次以及理論假設，它們可以通過句子的S結構產生。理想情況下，從S結構到LF 的映射操作與從D結構到S結構所需要的操作非常相似。

LF 具有一個模型論解釋。可以假定一個語句的LF 能夠直接通過一個相對簡單的組合性假設來解釋：詞項元素的解釋在詞庫中給出，短語節點的解釋是對其直接孩子節點的解釋的組合結果，其中組合通常是采用函項應用，但也允許一些其他的操作。

句法主義路線在語義方面，通常假定某種版本的蒙太格內涵邏輯，例如加林（D.Gallin）所開發的版本。通常將詞解釋為復雜函數，使用Lambda 項來陳述。由于采取的具體LF 形式不同，句法主義也存在很多的類型，然而整體上而言，句法主義相較于詞匯主義的不同有兩點：一是句法主義普遍允許在句法層次有更多的抽象；另一點是句法主義傾向于在句法生成的過程中消解語法與語義的不匹配。

我們以量詞轄域歧義的消解為例，來闡釋詞匯主義與句法主義在處理語法與語義界面問題中的異同點。例(16)是一個非常典型的量詞轄域的歧義句。句法主義方法主要采用量詞提升的方法，而詞匯主義方法采用的是豐富詞庫和語義本體的方法。

(16) 每個學生閱讀某篇論文。

(i)句法主義方法

在透明LF 方面中，QR可以將賓語量化詞置于主語量化詞的轄域內或者轄域外，產生兩個消岐的LFs，這兩個LFs 反過來產生兩個真值條件完全不同的解釋：

(17) a.LF1：[每個學生λ1[某篇論文λ2[t1閱讀t2]]]

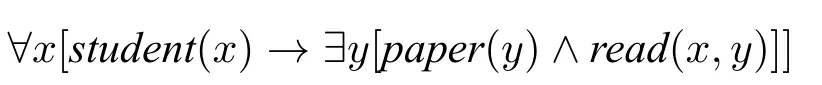
b.LF2:[某篇論文λ2[每個學生λ1[t1閱讀t2]]]

LF 分析為量化表達式產生所謂的前束范式，其中所有的量化詞出現在包含他們所約束變元的開放公式的前面。

(ii)詞匯主義的方法

在詞匯主義路線中，以CCG 為例，在對待(16)這樣的歧義消解采用豐富詞匯和語義本體的方法。我們對此采用CCG 方法進行歧義消解的嘗試。

(18) 每個:=(T/(TNP))/(T/NP):λP.λQ.?x.(P(x)→Q(x))

每個:=(T(T/NP))/(T/NP):λP.λQ.?x.(P(x)→Q(x))

(19) 某篇:=(T/(TNP))/(T/NP):λP.λQ.?x.(P(x)∧Q(x))

某篇:=(T(T/NP))/(T/NP):λP.λQ.?x.(P(x)∧Q(x))

其中T是一個范疇變量，可以取值S。

經過類型提升，我們就可以并行地推演例(16)中的語句。

根據上述例子，我們可以發現CCG 在處理量詞轄域主要是在范疇指派上進行靈活應對，通過詞條的不同范疇指派最終推演出表現轄域歧義的兩個語義解讀。

處理語法與語義的不匹配問題是語法與語義界面理論的核心，句法主義和詞匯主義的兩條不同進路代表著對待語法與語義界面的兩個不同方向。句法主義的進路偏重語法，將語義視為語法的一個影子，在遇到語法與語義的不匹配情形時，句法主義期望抽象語法，同時在句法生成過程中去解決不匹配問題。詞匯主義相對更平等地對待語法和語義，在遇到語法與語義的不匹配的情形時，詞匯主義期望通過豐富詞匯或者語義本體來解決不匹配問題。