分形集上的雙邊中點不等式
時統業
(海軍指揮學院, 江蘇 南京 211800)
0 引言

引理1[13]設f、g∈Dα(I),則有(f(x)+g(x))(α)=f(α)(x)+g(α)(x);(f(x)g(x))(α)=f(α)(x)g(x)+f(x)g(α)(x);(cf(x))(α)=cf(α)(x),其中c是常數;(f(g(x)))(α)=f(α)(g(x))(g′(x))α.
閉區間上的局部分數階連續函數是局部分數階可積的. 局部分數階定積分有與黎曼定積分類似的性質,如線性性質、區間可加性、比較性質、絕對不等式、牛頓-萊布尼茨公式、換元法、分部積分法等[14].

定義1[3]設區間I?R,函數f:I→Rα,若對任意u、v∈I和任意λ∈[0,1],有
f(λu+(1-λ)v)≤λαf(u)+(1-λ)αf(v),
則稱f是I上的廣義凸函數.
引理3[3]設f∈Dα(I),則下面條件等價:

引理4[3]設f∈D2α(a,b),則f是(a,b)上的廣義凸函數當且僅當對任意x∈(a,b)有f(2α)(x)≥0α.

引理6設n為自然數,則有(xnα)(α)=nαΓ(1+α)x(n-1)α.
證明當n=1時結論顯然成立. 假設n=k時結論成立,即(xkα)(α)=kαΓ(1+α)x(k-1)α,則根據引理1有
(x(k+1)α)(α)=(xkαxα)(α)=(xkα)(α)xα+xkα(xα)(α)=kαΓ(1+α)x(k-1)αxα+xkαΓ(1+α)=(k+1)αΓ(1+α)xkα.
即n=k+1時結論也成立,引理得證.

證明由引理6和引理2即可得證.
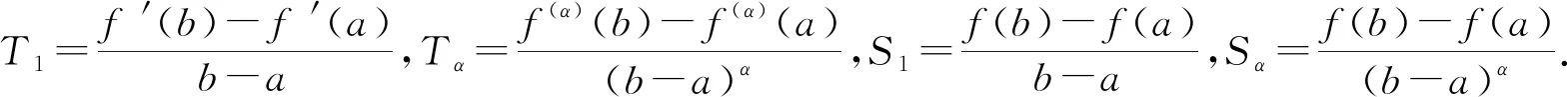
文[16]建立了恒等式
(1)
其中:f(x)在[a,b]上具有二階導數,且f″(x)在[a,b]上可積.
利用恒等式(1),文[16]給出中點積分公式的估計:
(2)
其中f是[a,b]上的二階可微函數,存在常數k和K使得k≤f″≤K.
文[17]利用恒等式(1)給出中點積分公式的另一個估計:
(3)
其中:f:[a,b]→R二次可微,對任意x∈[a,b]有k≤f″(x)≤K. 文[17]還舉例說明了式(2)與式(3)不分強弱.
引理8設區間I?R,I°是I的內部,f:I°→Rα,a、b∈I°,a (4) 證明使用兩次局部分數階分部積分法(引理2)得 (5) 類似可得 (6) 將式(5)與式(6)相加并整理,則式(4)得證. 本文受到文[18]所用方法的啟發,將給出分形集Rα上關于中點積分公式的新的雙邊不等式, 加強了不等式(2)和(3). 為證明本文主要結果,我們還需要下面的引理. 為方便起見,記 證明利用引理2,得 (7) 故由式(7)及k≤f(2α)≤K,有 則引理9得證. 定理1設f∈D2α[a,b],f(2α)∈Cα[a,b],且存在常數k、K∈Rα,k (8) 證明利用局部分數階分部積分法(引理2)得 (9) 由引理8和式(9)有 (11) 利用引理7得 (12) (13) (14) 綜合式(11)~式(14)得 于是有 (15) (16) (17) (18) (19) (20) (21) 綜合式(17)和式(21),則式(8)的右邊兩個不等式得證. 當k≤f(2α)≤K時,有-K≤(-f)(2α)≤-k. 對函數-f應用已證結論,則式(8)的左邊兩個不等式得證. 推論1設f:[a,b]→R二次可微,f″在[a,b]上可積,且存在常數k和K,k 定理2設f∈D2α[a,b],f(2α)∈Cα[a,b],且存在常數k、K∈Rα,k (22) 于是有 (23) (24) 推論2設f:[a,b]→R二次可微,f″在[a,b]上可積,且存在常數k和K,k (25) 證明在定理2中取α=1即可得證. 注2式(25)是式(2)和式(3)的加強.
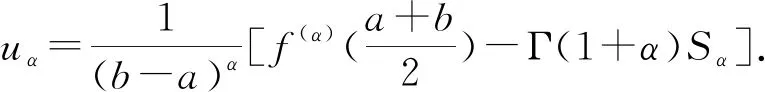
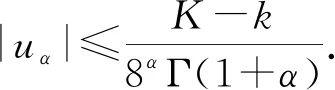
1 主要結果