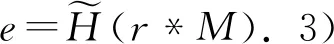新分?jǐn)?shù)階算子及其在密碼學(xué)上的應(yīng)用
陳興發(fā), 姚正安
(1. 廣東第二師范學(xué)院 數(shù)學(xué)系, 廣東 廣州 510303; 2. 中山大學(xué) 數(shù)學(xué)學(xué)院, 廣東 廣州 510275)
0 引言
現(xiàn)代密碼學(xué)理論大多建立在數(shù)論和交換群理論上. 例如:Diffie-Hellman密鑰協(xié)商方案[1]的安全性與離散對(duì)數(shù)求逆問題的困難性有關(guān); RSA公鑰加密方案的安全性與大素?cái)?shù)分解問題的困難性相關(guān). 目前Diffie-Hellman密鑰協(xié)商方案和RSA公鑰加密方案廣泛應(yīng)用在電子商務(wù)中. 這些公鑰的密碼學(xué)系統(tǒng)都是基于密碼學(xué)里的一個(gè)重要構(gòu)造──單向函數(shù). 簡單來講,單向函數(shù)f:A→B,是已知x∈A,計(jì)算f(x)∈B是容易的,但已知y=f(x)∈B,求x′∈x,滿足f(x′)=y是困難的. Diffie-Hellman密鑰協(xié)商方案中的離散指數(shù)就是單向函數(shù)的例子.
然而,Peter Shor[2]證明了量子計(jì)算機(jī)能在多項(xiàng)式時(shí)間里求解離散對(duì)數(shù)求逆問題和大素?cái)?shù)分解問題. 2019年10月23日,美國科技巨頭谷歌在《自然》雜志上刊登論文[3],宣稱其量子計(jì)算機(jī)已經(jīng)實(shí)現(xiàn)了“量子霸權(quán)”. 一旦量子計(jì)算機(jī)研制成功,這些基于離散對(duì)數(shù)求逆問題和大素?cái)?shù)分解問題構(gòu)造的密碼系統(tǒng)會(huì)被攻破. 量子計(jì)算的快速發(fā)展給經(jīng)典密碼學(xué)帶來了巨大沖擊,使得人們將目光投向了能夠抵抗量子計(jì)算機(jī)的攻擊的密碼體制研究[4].
G.B Blakley[5]提出將分析數(shù)學(xué)應(yīng)用到密碼學(xué)中,利用偏微分方程理論構(gòu)造熱流密碼體制. Hungerbühler[6]利用熱傳導(dǎo)方程:
(1)
構(gòu)造了一個(gè)基于熱力學(xué)第二定律的單向函數(shù),并且說明了這個(gè)單向函數(shù)能夠抵抗量子計(jì)算機(jī)的攻擊.
基于離散對(duì)數(shù)求逆問題和大素?cái)?shù)分解問題構(gòu)造的密碼系統(tǒng)是離散的,數(shù)據(jù)精確到一個(gè)比特值,只要有一個(gè)比特的值改變了都導(dǎo)致無法正常解密或驗(yàn)證. 而基于偏微分方程的密碼系統(tǒng)是連續(xù)的,允許有一定的冗余,數(shù)據(jù)出現(xiàn)微小變化時(shí),系統(tǒng)仍然可以正常解密或驗(yàn)證. 這樣的性質(zhì)使得連續(xù)的密碼系統(tǒng)可以在生物識(shí)別技術(shù)中有廣泛的應(yīng)用,因?yàn)槿说纳锾卣魅缰讣y、虹膜以及聲音等隨著時(shí)間會(huì)有微小變化,生物識(shí)別系統(tǒng)允許特征有微小變化的人通過,而其他顯著不同的就不能通過了.
我們用As代替方程(1)中的(-△)算子,并將方程(1)的邊界改為周期邊界:
(2)
然后說明方程(2)的解是適定的,但其反問題是不適定的,由此構(gòu)造出一個(gè)單向函數(shù),并將其應(yīng)用到數(shù)字簽名上.
1 基礎(chǔ)知識(shí)
1.1 基本不等式


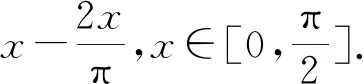

1.2 卷積的傅里葉級(jí)數(shù)


而


所以h(x)的傅里葉展開在x=x0處收斂于h(x0),從而有
1.3 圓上的Hilbert變換
設(shè)u在單位圓內(nèi)調(diào)和,則存在解析函數(shù)h且
h(z)=u(z)+iv(z), |z|<1,
v是u的共軛調(diào)和函數(shù),由C-R條件知v的共軛調(diào)和函數(shù)是-u. 根據(jù)泊松公式可得

則
當(dāng)r→1時(shí),
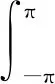
因此式是奇異積分,取主值意義,有
上述變換具有以下性質(zhì)[7-9]:
1)若f∈Lp,1 2)若|f(θ+δ)-f(θ)|≤K|δ|α,則|H(f)(θ+δ)-H(f)(θ)|≤C|δ|α. 首先利用圓上的Hilbert變換得出對(duì)以2π為周期的函數(shù)u(x)求二次導(dǎo)數(shù)的積分形式. 定理1若u(x)是2π為周期,且具有二次導(dǎo)數(shù),則 證明希爾伯特變換可得 而 又 則 由定理1可以定義一個(gè)新的分?jǐn)?shù)階算子As. 定義1 (3) 下面的引理4說明當(dāng)u滿足一定條件時(shí),As(u(θ))∈L([0,2π]). 引理4若u(x)∈C1,a,0≤s<2且a-s>-1,則存在M>0使得 I1的積分區(qū)域里沒有瑕點(diǎn),所以絕對(duì)可積,存在M1>0使得I1≤M1. 對(duì)于積分I2,當(dāng)ε充分小時(shí),利用微分中值定理和引理2可得 其中:x+α<ξ 由對(duì)稱性可知存在M3>0使得I3≤M3. 對(duì)于積分I4,當(dāng)ε充分小時(shí),利用u(x)∈C1,a和引理2可得 定理2若C是常數(shù),則As(C)=0,對(duì)任意n∈Z. 證明若C是常數(shù),顯然As(C)=0.下面計(jì)算As(cos(nx)). 其中: g(x,α,β)=cos(nx+nα+nβ)-cos(nx+nα)-cos(nx+nβ)+cos(nx)= 故 記 則 而 記 則 P(x)=-2Tn,ssin(nx), 記 下面計(jì)算Q(x). 最后 同理可得 定理2說明,常值函數(shù)、sin(nx)和cos(nx)(n∈Z)是As的特征向量. 下面估計(jì)Tn,s的界. 證明 下面的定理4說明了As具有分?jǐn)?shù)階性質(zhì). 證明先證Tn,s>Csns-1. 而 故 然后證明Tn,s≤C′sns-1. 利用引理2可得 I1≤C′1,sns. 同樣利用引理2,注意s>1,可得 所以I1≤C′2,sns. 綜上所述可知Tn,s≤C′sns-1. 其中:M1,s是僅與s相關(guān)的常數(shù). 其中:M2,s是僅與s相關(guān)的常數(shù). 證明計(jì)算As(u(x))可以分為3步: 1)I1(α,β,x)=Δα,β(u(x))=u(x+α+β)-u(x+α)-u(x+β)+u(x). 由計(jì)算As(sin(nx))的過程知 同理可得 綜上所述 類似地,可以得到定理6. 結(jié)合上述兩個(gè)定理,可得到推論1. As:HsL[0,2π], u(x) 證明f(x)∈Hs,g(x)∈Hs,則由Hs的定義可知f*g∈Hs. 結(jié)合引理3和推論1可知 其中: 當(dāng)k=0時(shí),R0(C)恒為常數(shù). 所以 下面討論方程 (4) 其中: 的解 同時(shí)由推論1可知 所以這樣的u(t,x)滿足方程(4). 定理10方程(4)的解 是穩(wěn)定和唯一的. 證明方程兩邊同乘u,并且對(duì)空間積分和時(shí)間積分可得 所以 假設(shè) 的解為uε(x),則可得 令φε(x)=φ(x)+ε,0<ε,得 即|u(t,x)-uε(t,x)|<ε,解的穩(wěn)定性得證. 假設(shè)方程有解u1、u2,則u=u1-u2也是方程的解,由上述計(jì)算可得 不等式右端為零,則u1=u2,方程解的唯一性得證,即方程是適定的. (5) 定理12方程(4)的反問題,即已知 (6) 證明u(0,x)是不適定的. 當(dāng)t=T時(shí), 設(shè)方程(4) 在T時(shí)刻的解為ω(x)=u(T,x). 1)連續(xù)性:由方程(4)的解的適定性(定理10)可知映射Gs,T是連續(xù)的. 2)線性性質(zhì):由于方程(4)是齊次方程,由解的疊加原理可知Gs,T(φ+ψ)=Gs,T(φ)+Gs,T(ψ). 3)卷積作用性質(zhì):由定理11可得Gs,T(φ*ψ)=Gs,T(φ)*ψ. 4)求逆困難:由定理12可知,在已知ω的情況,求φ滿足Gs,T(φ)=ω是困難的. 5.2.1Schnorr簽名方案[10] 由表1可以知道,Gs,T在某種程度上可以代替離散對(duì)數(shù). 現(xiàn)將Gs,T應(yīng)用到Schnorr簽名方案[10]中,得到基于新分?jǐn)?shù)階算子簽名方案. 表1 Gs,T與離散對(duì)數(shù) 5.2.2基于新分?jǐn)?shù)階算子簽名方案 密鑰生成:簽名私鑰φ,公鑰Y=Gs,T(φ). 簽名驗(yàn)證的正確性: 在文獻(xiàn)[11]中證明了在隨機(jī)預(yù)言模型下只要離散對(duì)數(shù)求逆是困難的,Schnorr簽名方案就是不可偽造的. 在文獻(xiàn)[12]中證明了在隨機(jī)預(yù)言模型下所有基于單向群同態(tài)的類Schnorr型簽名方案是不可偽造的. 所以我們提出的基于新分?jǐn)?shù)階算子簽名方案在隨機(jī)預(yù)言模型下也是不可偽造的,而且是基于一個(gè)更難的單向函數(shù)問題.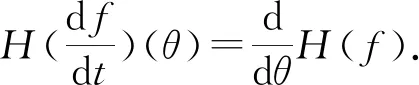

2 新分?jǐn)?shù)階算子的定義





3 新分?jǐn)?shù)階算子的性質(zhì)

3.1 新分?jǐn)?shù)階算子的特征向量

3.2 新分?jǐn)?shù)階算子的特征值的估計(jì)





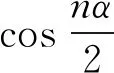
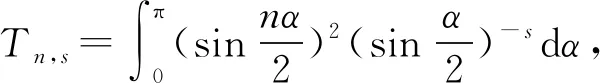



3.3 新分?jǐn)?shù)階算子的分析性質(zhì)





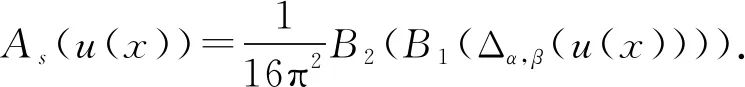



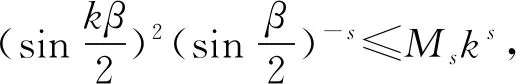




3.4 新分?jǐn)?shù)階算子的傅里葉系數(shù)



4 新分?jǐn)?shù)階算子拋物型方程









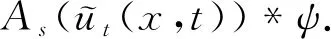



5 新分?jǐn)?shù)階算子在密碼學(xué)中的應(yīng)用
5.1 基于新分?jǐn)?shù)階算子拋物型方程的單向函數(shù)

5.2 基于新分?jǐn)?shù)階算子簽名方案