設參建模 深度整合

胡嫚玲

各位評委大家好，我說我將從以下五個方面展開說題，一說題目，二說學情，三說教學，四說推廣，五說價值。

1 ?說題目

如圖1，△ABC是一塊銳角三角形的材料，邊BC=120mm，高AD=80mm，要把它加工成正方形零件，使正方形的一邊在BC上，其余兩個頂點分別在AB、AC上，正方形零件的邊長是多少？

這道題出自于人教版九年級下冊《相似三角形復習題》57頁拓廣探索第11題，本題涉及到的知識點有相似三角形的判定和性質，正方形的性質等。

該題目之所以出現在相似這一章的拓廣探索復習題上，不僅是考察學生對本章所學能否應用于實踐探索，更是對設參思想，建模思想的考察，也透露出數學與生活息息相關。

本題是設參，通過相似比例關系得到含有參數的方程，在解題時，通過以疑激趣，以疑啟思，在精心設問下引發學生主動思考和探究，合理聯想，突破解題思路，增強解題能力，提升數學思維，從而提高學生數學抽象、邏輯推理、數學建模、直觀想象、數學運算等核心素養的發展。

2 ?說學情

學生對相似的性質和應用基本掌握，但在復雜情況下，對相似的模型識別能力欠缺，審題意識和能力不強，尤其對于隱含條件的挖掘比較欠缺，通過適時設參，轉化為方程乃至函數，這種解決問題的經驗缺乏，模型積累較少，因而造成學生對此題心生畏懼，容易回避。

3 ?說教學

受波利亞解題表中第一步弄清題意，第二步擬訂計劃，第三步實行計劃，第四步回顧的啟發，結合本題的實際背景，將本題的解題策略，分為以下5個環節1.思維鋪墊，2.分析題目，3.關鍵點突破，4.解題過程，5.回顧梳理

3.1思維鋪墊

首先以思維導圖（圖2）的形式來對本章的知識點進行回顧，在導圖中，有意強調與本題相關聯的點，為此題的解決做準備工作。

3.2分析題目

有研究顯示，做一道題有70%的時間都應該在認真審題，所以此題的解題教學以問題驅動的方式幫助學生理解題意，進行審題分析;

3.3關鍵點突破

此題的關鍵點在于，一對應邊的比等于對應高的比，二設參法，在學生由平行得到相似這一認知基礎上，當學生分析到題中給的條件由底邊BC，高AD，在圖1中予以做標記，以此來提示學生，聯想到對應底邊的比等于對應高的比，在分析基本圖形時，指出與正方形相等的邊長KD恰好于大三角形的高AD重合，在對應邊的比等于對應高的比的基礎上，就可以用設參法列出關于邊長的等量關系;

3.4解題過程

由學生到黑板上演示此題的解題過程，老師對其解題過程進行評價，以幫助其養成良好的解題習慣;

3.5回顧梳理

再由老師對本題的解題思路進行總結，為此題的變式做準備。

下面是我的教學實錄

4 ?說推廣

波利亞在《怎樣解題中》指出：“變化問題使我們引進新的內容，從而產生新的接觸，產生和我們問題有關的元素接觸的新的可能性”，之所以選擇這道題目，因為我發現在9上課本在實際問題與二次函數的復習鞏固第六題習題中發現了類似的圖形（圖3）。

而這道題的考點是通過設參，建立二次函數模型，用二次函數性質來解決，從這里給了我靈感，大膽對第11題進行變式，新課標提出培養學生應用意識和模型思想，要求我們關注數學模型，從生活中來，到生活中去解決問題，我決定構設相似場景，把正方形變為矩形，解決在節約型社會下提倡物盡其用，如何截取才能使得矩形面積最大的問題。

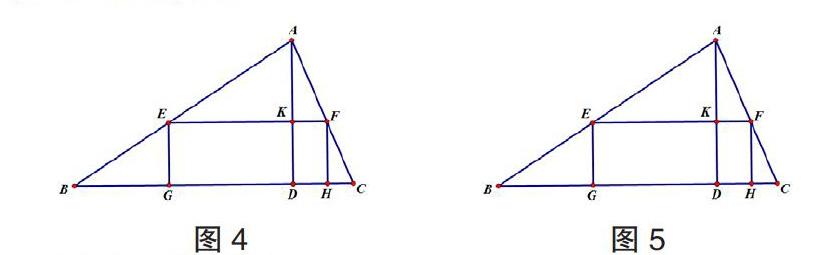
變式1：如圖4，△ABC是一塊銳角三角形的材料，邊BC=120mm，高AD=80mm，要把它加工成矩形零件，使矩形的一邊在BC上，其余兩個頂點分別在AB、AC上，如何裁剪，使矩形面積最大？最大面積是多少？

對變式1的教學流程

4.1自然過渡，將正方形變為矩形，如何截取，才能使得矩形面積最大？

4.2用動態圖幫助學生分析題目，讓學生在動態圖的基礎上理解面積變是由于長和寬在變，所以本題有三個變量;

4.3求面積最大值，要用二次函數，而二次函數是兩個變量;

4.4本題的題眼就要借助上一題的思路利用相似模型在于找到長和寬的等量關系;

4.5三個變量減少為兩個變量，就可以用二次函數模型來求最值。

設計意圖：要想用二次函數解決矩形面積最大值，就要借助原題中的相似模型找到長和寬的等量關系，再用二次函數模型解決最值問題，在一道題中，對不同的數學模型，通過設參建模，進行整合，讓學生在原有認知的基礎上，對此題進行深度理解。

下面是我的教學實錄

在變式1基礎上，由特殊到一般，繼續設參，底邊a，高為h，類比變式1可得變式2的教學流程;

變式2：如圖5，△ABC是一塊銳角三角形的材料，邊a，高h，要把它加工成矩形零件，使矩形的一邊在BC上，其余兩個頂點分別在AB、AC上，如何裁剪，使矩形面積最大？最大面積是多少？

1.將底和高換為字母;

2.類比上一題的解題思路即可求得題思路，師生共驗證猜想。

設計意圖：以變式1為原型，再次對一道題中不同數學模型通過設參進行深度整合，讓學生體驗攻堅克難的過程，樹立其對數學的信心

下面是我的教學實錄

5 ?說價值

義務教育數學課程標準（2011年版）旗幟性理念是培養學生的創新意識，提倡教學生學會思考，學會學習，通過原題的詳細解決過程，變式1.2的適度延伸和探究，旨在讓學生對問題有一個由淺入深的認識過程，在這個認識過程中對不同數學模型進行整合，讓學生體會不同數學模型，在一道題目中存在時，能發現并提出新的問題，進而去分析和解決問題，這樣的習題教學更是培養學生在遇到困難時攻堅困難，尋根問底，理性分析等良好數學品格的契機。

更重要的是能在不改變問題情境的狀況下，自然過渡與切合，讓學生意識到數學的“有用”，體會到解決問題幫助他人的愉悅感，為社會進步作出小貢獻的成就感，會更增添學好數學，用好數學的決心。