換元法在初中數學解題中的應用

賴振華

(福建省平和縣文峰中學 363700)

在初中數學新課程標準中明確提出，初中數學的學習首要目標就要求學生在學習的過程中，獲得必備的數學基礎知識、數學基本技能等，并對最基本的數學概念、數學結論的本質等進行理解，進而充分體會初中數學中所蘊含的數學思想和數學方法等.因此，在初中數學教學中，必須要充分借助“換元法”以提升學生的解題效率.

一、換元法概述

換元法又稱之為輔助元素法、變量代換法，主要是將某一個式子看做成一個整體，并用另一個變量去代替它.換元的實質就是轉化，是用一種變數形式對另一種變數的形式進行取代，進而使得問題得到了有效的簡化.可以說，在使用換元法這一方法對初中數學問題進行解答的時候，其關鍵就在于合適地選擇出“新元”，并將其引入到數學問題中進行適當的代換，進而找到數學問題的解題思路.

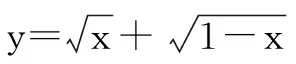
總而言之，在對數學問題進行解決的過程中，換元法是最為常用的數學解題方式.通過換元法的應用，使得整個數學運算更加簡便，進一步提升了學生的解題效率.

二、換元法在初中數學解題中的具體應用

1.在因式分解中的應用

在初中數學知識體系中，多項式的因式分解歷來是教學、考試的重點.就因式分解這一部分的內容來說，雖然總體難度不是特別大，但是涉及到的基礎知識卻非常多.例如：加減乘除、平方、代數式等，學生在進行該部分數學問題的解決過程中，必須要對因式分解與整式乘法之間的關系，并對新舊知識之間的比較進行探索，進而掌握因式分解的主要方法.

而在進行因式分解問題解答的過程中，換元法則是學生最為常用的方法，并深得學生的青睞.具體來說，換元法在因式分解中應用的時候，首先應將原代數式中的某個部分，用新元對其進行代替，以達到減少因式項數的目的，進而使得問題變得更加簡單.

2.在解方程組問題中的應用

方程組也是初中數學中最為重要的內容，在對這部分數學問題進行解答的時候，學生只有明確找出未知條件、已知條件兩者的關系，或者將方程組中所隱蔽的已知條件之間的關系進行明確的時候，才能將新知識進行轉化，使其成為舊知識，進而對其進行有效的解決.而在這一過程中，則離不開換元法的應用.

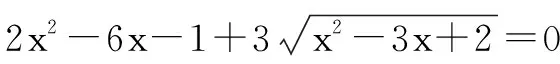
3.在整式運算中的應用

在初中數學學習中，整式運算是學生最為常見的運算問題，同時整式運算也相對比較復雜.許多學生面對這一問題，常常無從下手，不知道如何對其進行解決.據此，教師在引導學生對其進行解答的時候，可充分借助換元法的形式，將相同的部分看做一個整體，并利用新元對其進行替代，進而這一復雜的問題進行轉換，使其成為一個簡單的數學問題.

例如，在對(1-2-3-…-998)(2+3+4+…+999)-(1-2-3-…-999)(2+3+4+…+998)這一整式進行運算的時候，就可以充分借助換元法，將(2+3+4+…+999)設置為a，將(2+3+4+…+998)設為b，那么該整式運算就會簡化為(1-b)a-(1-a)b，進而使得整個整式運算更加簡單.

綜上所述，在初中數學學習中，學生經常會遇到比較復雜的數學問題，如果直接按照原始的方式對其進行求解，不僅使得數學問題變得十分棘手，并且致使學生在對數學問題進行解決的過程中，常常出現無從下手、頻頻出現錯誤等現象.因此，在指導學生對這些數學問題進行解決的過程中，就可以引導學生充分借助換元法的方式，將復雜的數學問題進行簡化，進而促使學生對其進行順利解決.