汽車滑動門外偏量模型研究

周福榮 劉晶

【摘 要】文章對滑動門外偏量進行模型簡化，通過簡化模型得出不同位置外偏量與導軌分布的數學關系，根據得出的數學關系指導滑動門前期設計;定義了滑動門車門姿態，通過簡化模型量化了車門姿態的評估方法，可用于分析和指導實際生產中車門姿態的調整。

【關鍵詞】汽車;滑動門;外偏量

【中圖分類號】U463.834 【文獻標識碼】A 【文章編號】1674-0688（2020）03-0044-02

0 前言

滑動門作為汽車常用的側門類型，普遍應用在微型商用車、商務MPV，滑動門約束條件的特殊性決定了開啟的平順性，成為評估車門性能的重要指標[1]，而與平順性關聯的外偏量則是評估車門的直觀數據，因此研究滑動門外偏量及其簡化模型，在設計和實際生產中有著重要的指導意義。

1 滑動門系統相關定義

1.1 汽車滑動門的定義

汽車滑動門是通過上走輪臂、中走輪臂和下走輪臂分別在上導軌、中導軌和下導軌沿著固定軌跡移動的車門[2]。

1.2 最小外偏量的定義

能夠保證滑動門正常打開的最小Y向車門位移，用D表示，該位移量與3個因素有關，分別是門厚度A，運動安全距離B、門上附件Y向高度H，其關系如下：

D=A+B+H（1）

1.3 滑動門運動模型的基本形式

簡化的滑動門運動模型有兩種：第一種是上、中、下導軌處車門的外偏量相同，該種模型是理想的運動模型，能夠保證車門打開時車門上所有部件不存在相對移動，即車門完全平移打開。第二種是上、中、下導軌處車門的外偏量不同，外偏量由上到下逐漸增加，該種模型是實車普遍采用的模型，在車門打開時，車門會在X-Z平面小角度傾斜后再進行平移[3]。

1.4 滑動門車門姿態

因為上、中、下導軌處車門外偏量不同，所以車門打開后在X-Z面上呈現小角度的傾斜，此時車門X方向的不同位置外偏量也會有差異，主要體現在滑動門前上角與后上角Y向差異，前下角和后下角Y向差異，以上差異在評估滑動門開啟狀態時稱之為車門姿態。

2 滑動門不同位置外偏量關系

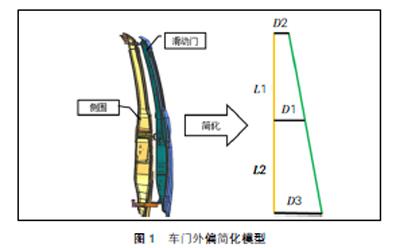
一般確定滑動門最小外偏量的區域在中導軌位置，主要影響部件為搖窗機手柄或扶手臺，以上零件在車門正常打開時的最小Y向位移確定為該車的最小外偏量。為保證側圍沖壓要求和走輪臂的垂直剛度要求，一般在設計時會盡量壓縮該處尺寸，即保證該處沖壓和剛度要求的前提下使該處外偏量實現最大化，該處最小外偏量用D1表示。

上導軌位置的外偏量主要受車身內頭部空間和導軌支撐件的沖壓要求決定，其中頭部空間要求是決定性因素，增大該處外偏量會直接壓縮乘員頭部空間，進而不滿足總布置要求。此外，考慮到沖壓板材拉延成型的實際情況，應適當減小外偏量。對于上導軌位置的外偏量一般按照平臺化處理，即一個平臺采用一個定值進行設計，可以更好地規避設計風險。該處最小外偏量用D2表示。

下導軌位置的外偏量主要由車身大梁Y向布置和車門下部扭轉要求決定，車身的承載性要求是車輛設計的重點，下導軌的布置需要在不影響大梁布置的前提下進行，因此下導軌前端應在Y向盡量靠近大梁，滿足導軌支架焊接操作空間及安全距離即可;此外，下導軌直線段的-Y向應盡量向滑動門內板靠近，保證滑動門下部扭轉剛度滿足要求即可。該處最小外偏量用D3表示。

在Z方向上，上導軌的布置受滑動門分縫和門洞影響;中導軌布置主要受造型影響;下導軌的布置受地板和滑動門下部門洞影響;上導軌到中導軌的Z方向距離用L1表示;中導軌到下導軌的Z方向距離用L2表示。

車門外偏量、導軌分布數模及簡化模型Ⅰ如圖1所示。

模型Ⅰ中外偏量和導軌分布的關系如下：

（D1-D2）/（D3-D2）=L1/（L1+L2））（2）

假設上走輪臂處外偏量D2不變，如果中導軌處車門外偏量增加Δ，下導軌處外偏量增加值X，由公式（2）可得出：

X=（L1+L2）Δ/L1（3）

通過模型簡化得出公式（3），可以看出中走輪臂位置增加外偏量與下走輪臂處外偏量為正相關，且增加量只與上、中、下導軌的分布相關。

3 調整外偏量對車門姿態的影響

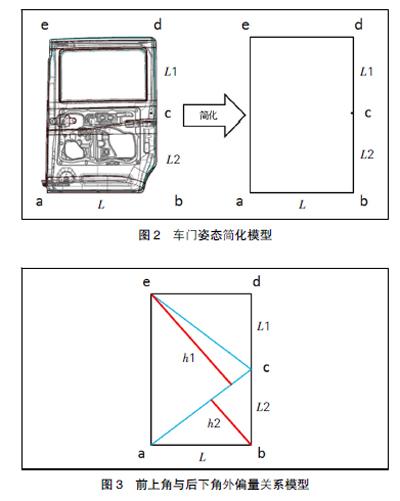
在實際設計過程中，Y向可調整的走輪臂主要是上走輪臂和下走輪臂，中走輪臂外偏量一般不可調整，以下分析調整上、下導軌外偏量對車門姿態的影響。車門簡化模型Ⅱ如圖2所示，其中上、中、下走輪臂位置分別為e、c和a，門寬為L，上導軌到中導軌的Z方向距離用L1表示;中導軌到下導軌的Z方向距離用L2表示，其中e、a、d和b又分別稱為滑動門前上角、前下角、后上角和后下角。

分析上走輪臂處外偏量對車門姿態的影響，調整上走輪臂外偏量，且中走輪臂和下走輪臂均按照固定形式，即調整上走輪臂時，前上角e會繞著ac連線以e到ac的垂線h1為半徑進行轉動;同時，后下角b會以ac連線以b到ac的垂線h2為半徑進行反向轉動;當調整上走輪臂e處外偏量Δ時，后下角外偏量y與Δ的關系如圖3所示。

y=（h2/h1）Δ

其中，

h1=（L1+L2 L/■;h2=L2 L/■

y=L2Δ/（L1+L2）（4）

同樣，可采用相同模型評估下走輪臂外偏量對車門姿態的影響，當調整下走輪臂a處外偏量Δ時，后上角外偏量y與Δ的關系如下：

y=L1Δ/（L1+L2）（5）

通過模型簡化得出公式（4）和公式（5），可以看出上走輪臂位置外偏量與后下角外偏量為正相關，下走輪臂位置外偏量與后上角外偏量呈負相關;且變化量只與上、中、下導軌的分布相關。

4 總結

簡化的滑動門外偏量模型Ⅰ在車門子系統設計前期可以快速得出下導軌位置外偏量具體數值，能夠更直接地評估工程和造型可行性，減少工程和造型反復，縮短產品開發周期;簡化的滑動門外偏量模型Ⅱ定義了滑動門車門姿態，量化了車門姿態的工程描述;此外，該模型可用于指導實際生產中滑動門調整，使實際操作有準確的理論依據。

參 考 文 獻

[1]滕平，劉晶.基于UG的滑動式車門運動軌跡平順性分析方法[J].企業科技與發展，2018（10）：92-93.

[2]周福榮，施華灘，韋逢義，等.滑動門上走輪臂與上導軌干涉問題研究[J].企業科技與發展，2015（3）：24-26.

[3]劉鵬飛.汽車滑移門系統的運動學和多剛體動力學建模與參數優化[D].上海：上海交通大學，2013.