單原子Lennard-Jones體黏彈性弛豫時(shí)間*

汪楊 趙伶玲

(東南大學(xué)能源與環(huán)境學(xué)院， 能源熱轉(zhuǎn)換及其過程測(cè)控教育部重點(diǎn)實(shí)驗(yàn)室， 南京 210096)

(2020 年1 月19日收到; 2020 年4 月3日收到修改稿)

采用平衡態(tài)分子模擬的方法， 從微觀角度對(duì)溫度 —5、密度 = 0.85—1、勢(shì)參數(shù)ε = 0.97—1和σ = 0.8—1.3范圍內(nèi)22組液固共存態(tài)及液態(tài)單原子Lennard-Jones (L-J)體的黏彈性弛豫時(shí)間進(jìn)行了研究， 計(jì)算了單原子L-J體的靜態(tài)黏彈性(黏度η*、無限大頻率的剪切模量 )及動(dòng)態(tài)黏彈性(儲(chǔ)能模量 、損耗模量 )等特性參量， 并在此基礎(chǔ)上分析了黏彈性特征弛豫時(shí)間、Maxwell弛豫時(shí)間及原子連通弛豫時(shí)間. 此外， 本文根據(jù)系統(tǒng)內(nèi)原子的排布情況， 應(yīng)用Kramers逃逸速率理論描述原子的擴(kuò)散、匯聚過程， 提出并建立了一種單原子L-J體黏彈性弛豫時(shí)間的預(yù)測(cè)方法. 結(jié)果表明: 在單原子L-J體系統(tǒng)中， 低溫情況下，Maxwell弛豫時(shí)間與黏彈性特征弛豫時(shí)間差異明顯; 原子連通弛豫時(shí)間與黏彈性特征弛豫時(shí)間結(jié)果接近， 但原子連通弛豫時(shí)間的計(jì)算過程需耗費(fèi)大量時(shí)間和計(jì)算資源; 預(yù)測(cè)方法得到的弛豫時(shí)間與黏彈性特征弛豫時(shí)間的結(jié)果更為接近. 本文提出的單原子L-J體黏彈性弛豫時(shí)間的預(yù)測(cè)方法具有一定的準(zhǔn)確性和可靠性， 可為材料黏彈性弛豫時(shí)間的研究提供一種新的思路.

1 引 言

黏彈性是物質(zhì)的重要性質(zhì). 一般而言， 任何材料都具有彈性和黏性， 但會(huì)因溫度和作用力速率不同， 或主要表現(xiàn)為彈性(低溫或作用時(shí)間快)， 或主要表現(xiàn)為黏性(高溫或作用時(shí)間慢)[1]. 黏彈性的本質(zhì)是由于材料內(nèi)分子運(yùn)動(dòng)具有弛豫特性， 當(dāng)材料受外力作用時(shí)， 其分子響應(yīng)與外力達(dá)不到平衡， 從而產(chǎn)生了黏彈性[2]. 因此， 黏彈性弛豫時(shí)間是表征材料黏彈性響應(yīng)的重要概念， 且與物質(zhì)微觀原子間相互作用直接相關(guān). 如何更好地對(duì)黏彈性弛豫時(shí)間進(jìn)行表征和獲取， 對(duì)物質(zhì)黏彈特性的研究具有重要的意義.

目前， 研究者們對(duì)于黏彈性弛豫時(shí)間的表征定義主要有三種方法: 黏彈性特征弛豫時(shí)間、Maxwell弛豫時(shí)間、原子連通弛豫時(shí)間.黏彈性特征弛豫時(shí)間是材料儲(chǔ)能模量與損耗模量的交點(diǎn)頻率對(duì)應(yīng)的時(shí)間， 其表征的是材料表現(xiàn)出顯著黏彈性的時(shí)間尺度[3]. Sunthar[4]指出在振蕩實(shí)驗(yàn)中， 低頻狀態(tài)下(或長(zhǎng)時(shí)間響應(yīng))匯聚物的儲(chǔ)能模量(彈性)總大于損耗模量(黏性)， 而在高頻狀態(tài)下(或短時(shí)間響應(yīng))， 匯聚物主要展現(xiàn)出黏性特征， 儲(chǔ)能模量與損耗模量的交點(diǎn)頻率對(duì)應(yīng)的時(shí)間即為黏彈性特征弛豫時(shí)間. Agrawal等[5]采用分子模擬的方法， 在類似的黏彈動(dòng)態(tài)模量分析的基礎(chǔ)上， 運(yùn)用傅里葉變換得到了高分子物質(zhì)聚脲的儲(chǔ)能及損耗模量的數(shù)據(jù)， 其模擬結(jié)果與加載應(yīng)力實(shí)驗(yàn)結(jié)果一致， 證明了應(yīng)用分子模擬的方法可以開展黏彈性弛豫時(shí)間的研究. Maxwell弛豫時(shí)間是目前最常見的用來計(jì)算物質(zhì)黏彈性弛豫時(shí)間的方法， 已有研究學(xué)者應(yīng)用分子模擬的方法開展了Maxwell弛豫時(shí)間的相關(guān)研究. Hartkamp等[6]運(yùn)用Green-Kubo公式[7，8]計(jì)算了簡(jiǎn)單原子流體的黏度、無窮大頻率的剪切模量、Maxwell弛豫時(shí)間等黏彈性物理量， 并得到了與動(dòng)力學(xué)理論預(yù)測(cè)類似的結(jié)果. Guillaud等[9]采用TIP4P/2005f力場(chǎng)模擬了大范圍溫度下超冷水的弛豫行為， 結(jié)果顯示當(dāng)溫度低于285 K時(shí)， Maxwell弛豫時(shí)間無法表征超冷水的弛豫行為. 近年來， 為分析黏彈性的產(chǎn)生機(jī)理，有些研究學(xué)者基于對(duì)分子擴(kuò)散、匯聚過程的研究來描述黏彈性弛豫時(shí)間. Iwashita和Egami[10]首次提出了原子連通弛豫時(shí)間的概念去描述粒子得到或者失去自身周圍最近的粒子過程， 并將各類液態(tài)金屬向玻璃態(tài)轉(zhuǎn)化過程中的Maxwell弛豫時(shí)間和原子連通弛豫時(shí)間進(jìn)行比較[11]， 結(jié)果顯示二者在高溫下比較接近， 但在低溫下原子連通弛豫時(shí)間更能反映物質(zhì)黏彈性的響應(yīng). Ashwin和Sen[12]在分析Yukawa液體內(nèi)Maxwell弛豫時(shí)間和原子連通弛豫時(shí)間的過程中指出原子連通弛豫時(shí)間是系統(tǒng)內(nèi)剪切應(yīng)力松弛的微觀起源.

綜上所述， 在上述三種表示黏彈性弛豫時(shí)間的方法中， 黏彈性特征弛豫時(shí)間最符合表征材料黏彈性響應(yīng)的概念， 但是需要計(jì)算不同頻率下物質(zhì)的儲(chǔ)能模量和損耗模量， 計(jì)算時(shí)間長(zhǎng)、計(jì)算過程復(fù)雜.Maxwell弛豫時(shí)間的計(jì)算簡(jiǎn)單， 但其描述受到Maxwell模型[13]的限制而無法應(yīng)用于更廣泛的物質(zhì)[14]. 原子連通弛豫時(shí)間能夠從微觀角度解釋剪切應(yīng)力松弛產(chǎn)生的原因， 但其計(jì)算過程需要耗費(fèi)大量計(jì)算資源統(tǒng)計(jì)原子的運(yùn)動(dòng)軌跡. 因此， 進(jìn)一步開展計(jì)算物質(zhì)黏彈性弛豫時(shí)間方法的研究具有重要的意義.

2 研究對(duì)象及方法

2.1 對(duì)象及方法

為方便對(duì)計(jì)算結(jié)果進(jìn)行更好的分析， 本文中的物理量均采用“約化單位”[15]， 用上標(biāo)“*”表示， 如T*=Tk/ε，ρ*=ρσ3，，r*=r/σ，，η*=ησ3/. 其中ε和σ為 L-J勢(shì)參數(shù)， 分別表示勢(shì)能為0時(shí)的原子距離、勢(shì)能阱深度;m為原子質(zhì)量;T為真實(shí)單位下的溫度， 單位為 K;ρ表示密度， 單位為 mol/L;p為壓強(qiáng)， 單位為 MPa;為黏度， 單位為μPa·s.

本文建立的單原子L-J體系統(tǒng)采用周期性邊界條件[16]， 計(jì)算域尺寸 (模擬盒子)為 16 × 16 ×16單位體積， 并按照相應(yīng)的密度設(shè)置盒子內(nèi)的粒子數(shù)量， 如圖1所示.

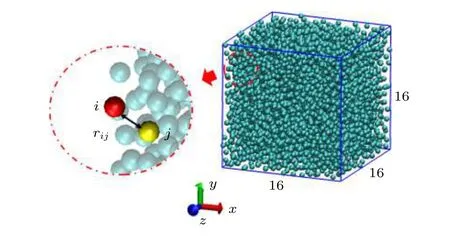
圖 1 L-J體計(jì)算系統(tǒng)Fig. 1. L-J fluid simulation system.

L-J體系統(tǒng)內(nèi)分子間僅受范德瓦耳斯力的作用， 其具體勢(shì)能函數(shù)[17]為

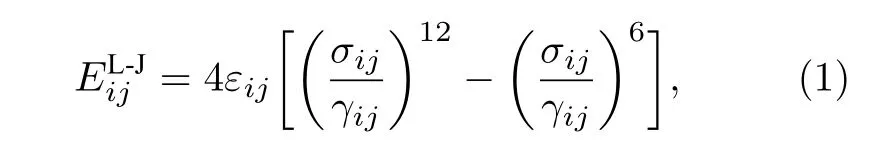
式中rij為原子i與j之間的距離，εij為勢(shì)能阱的深度，σij為兩體互相作用的勢(shì)能為零時(shí)的距離.其中

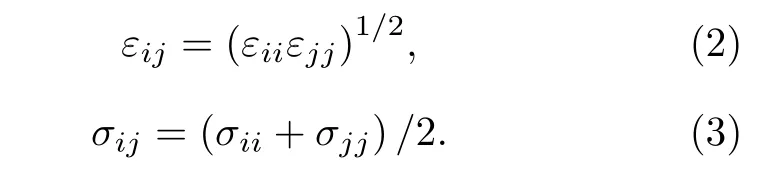
范德瓦耳斯力作用截距半徑設(shè)置為5.0[18].

系統(tǒng)中原子的運(yùn)動(dòng)受牛頓第二定律及非哈密動(dòng)量方程控制， 采用正則系統(tǒng)[19]條件， 時(shí)間步長(zhǎng)設(shè)為0.003. 模擬總時(shí)間步數(shù)為108步， 系統(tǒng)經(jīng)過5 × 107個(gè)時(shí)間步長(zhǎng)后達(dá)到平衡， 本文選取平衡后系統(tǒng)的數(shù)據(jù)進(jìn)行分析， 并統(tǒng)計(jì)了系統(tǒng)內(nèi)所有粒子在最后500個(gè)時(shí)間步長(zhǎng)內(nèi)的運(yùn)動(dòng)軌跡. 本文應(yīng)用LAMMPS[20]軟件進(jìn)行建模和具體計(jì)算.

2.2 數(shù)據(jù)處理方法

本文采用 Green-Kubo 公式[7，8，21]計(jì)算黏度:

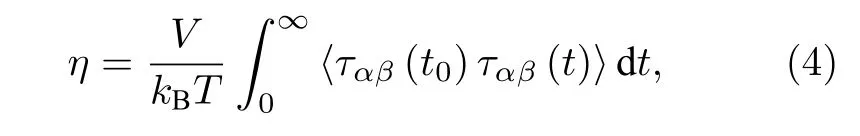
式中V表示體積;kB為玻爾茲曼常數(shù);T為熱力學(xué)溫度;t表示時(shí)間;ταβ表示剪切應(yīng)力張量的非對(duì)角元素， 其具體表達(dá)式為

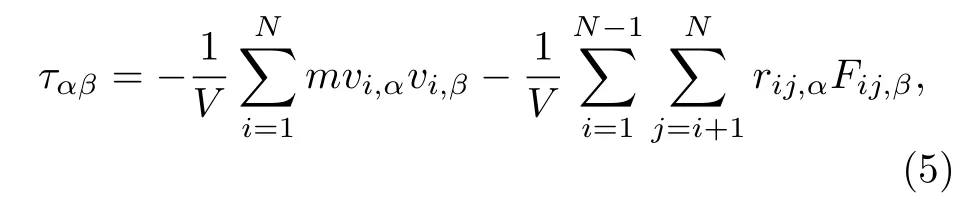
黏彈性動(dòng)態(tài)模量G(t)可通過應(yīng)力自相關(guān)函數(shù)公式進(jìn)行計(jì)算[22]:

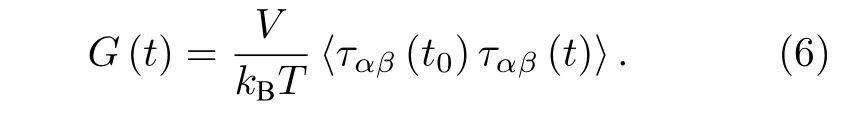
運(yùn)用傅里葉變換公式將(6)式轉(zhuǎn)換為復(fù)數(shù)型頻域剪切模量函數(shù)G(ω):

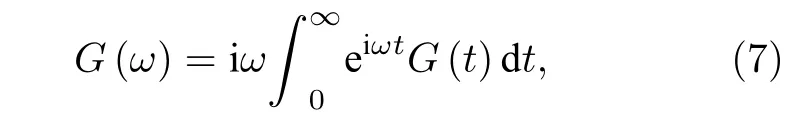
其中無窮大頻率剪切模量[6]定義為

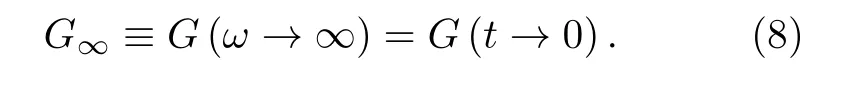
(7)式中復(fù)數(shù)模量的實(shí)部為儲(chǔ)能模量((9)式)[23]， 其反映材料形變時(shí)的回彈能力[24]， 即彈性:

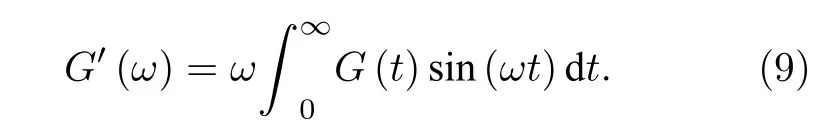
(7)式中的虛部實(shí)質(zhì)為損耗模量((10)式)[25]， 反映材料形變時(shí)內(nèi)耗程度， 即黏性:

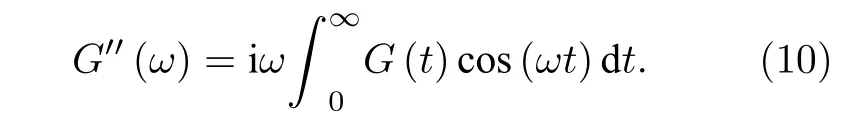
本文應(yīng)用Einstein關(guān)系式[26]計(jì)算得到系統(tǒng)的擴(kuò)散率D為

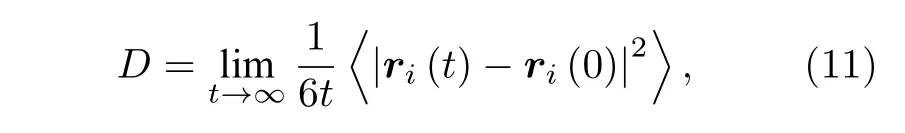
其中t表示時(shí)間;r表示原子的位移; 〈·〉表示組內(nèi)所有原子的平均.

2.3 模型驗(yàn)證

為保證模擬的準(zhǔn)確性， 本文主要從物質(zhì)的黏度、系統(tǒng)原子的排布規(guī)律兩方面對(duì)所建立的模型和計(jì)算方法進(jìn)行驗(yàn)證.

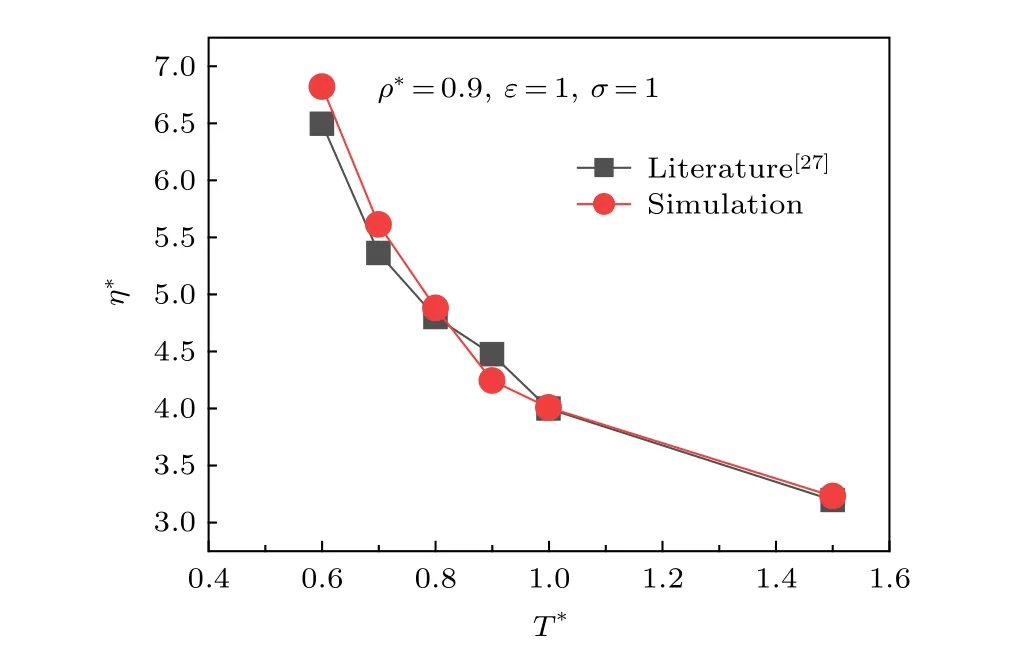
圖 2 不同溫度下L-J體的黏度驗(yàn)證Fig. 2. Verification of viscosity of L-J fluid at different temperatures.

為驗(yàn)證模型在微觀結(jié)構(gòu)上是否準(zhǔn)確， 本文從L-J體的原子排布出發(fā)， 對(duì)系統(tǒng)的徑向分布函數(shù)進(jìn)行驗(yàn)證. 計(jì)算了多種物性參數(shù)情況下單原子L-J體的徑向分布函數(shù)， 其中兩種不同溫度下的單原子L-J體的徑向分布函數(shù)與Morsali等[28]經(jīng)驗(yàn)公式的對(duì)比結(jié)果示于圖3. 由圖3可以看出， 本文中的模擬結(jié)果與相同溫度密度條件下的文獻(xiàn)數(shù)據(jù)[28]十分符合， 且反映出徑向分布函數(shù)曲線隨溫度變化的共同趨勢(shì): 在密度為1的情況下， 溫度為0.9時(shí)(圖3(a))， 徑向分布函數(shù)曲線擁有多個(gè)波峰波谷，數(shù)值波動(dòng)明顯， 在， 2.0， 2.8， 3.7， 4.8 依次出現(xiàn)峰值逐漸降低的波峰， 原子排布不規(guī)則， 屬于黏彈性顯著的固液共存態(tài); 當(dāng)溫度升高至4時(shí)(圖3(b))， 徑向分布函數(shù)曲線發(fā)生明顯變化， 曲線平滑， 數(shù)值波動(dòng)減小， 波峰波谷數(shù)量顯著減少， L-J體處于液態(tài).

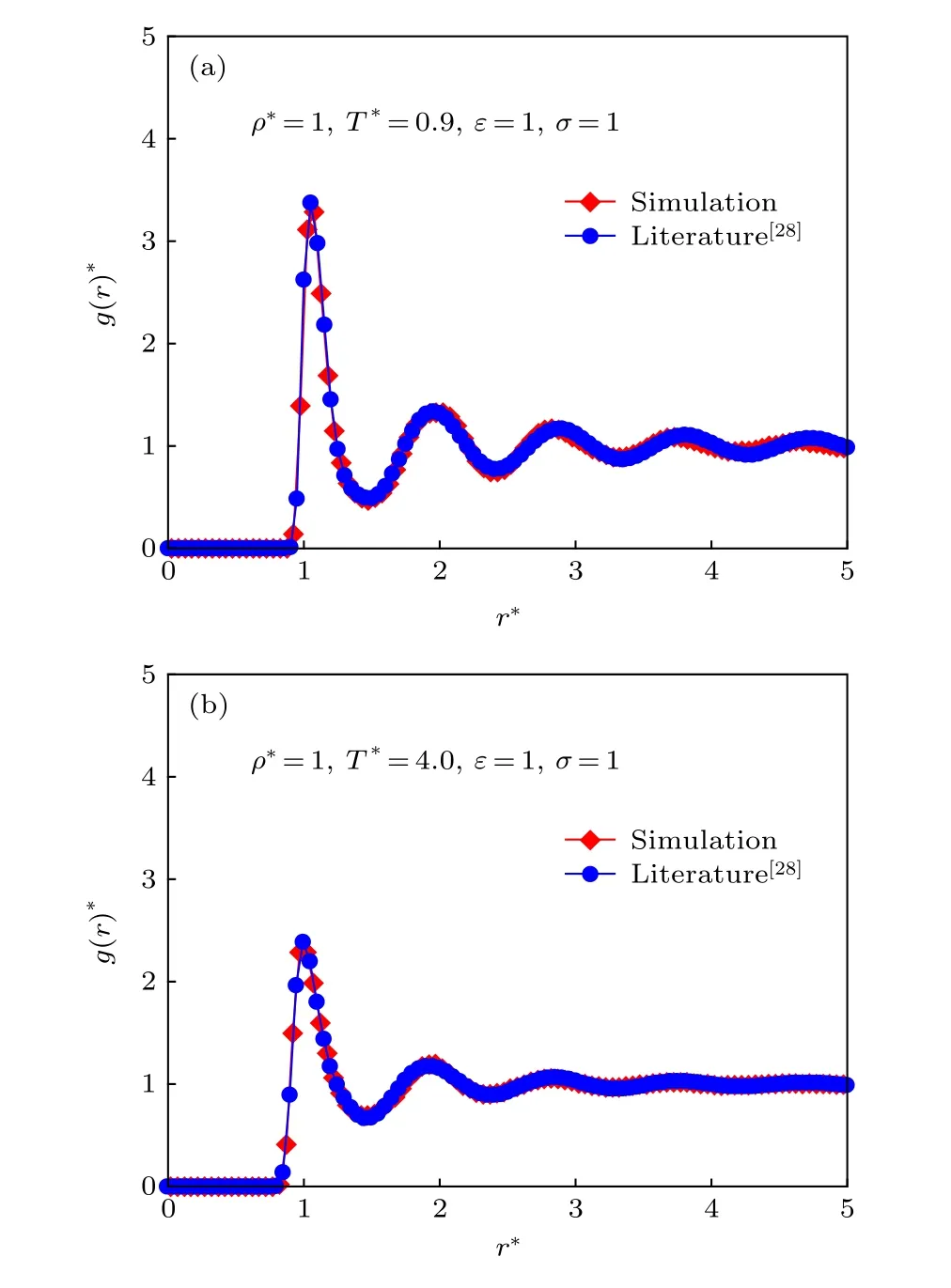
圖 3 L-J體的徑向分布函數(shù)驗(yàn)證 (a) ;(b)Fig. 3. Verification of the radial distribution function of L-J fluid: (a) ; (b) .

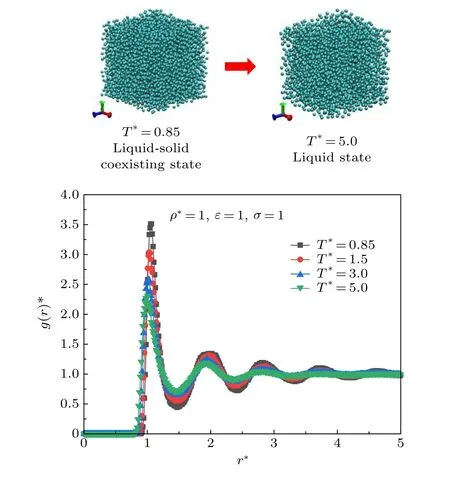
圖 4 時(shí)不同溫度下L-J體的徑向分布函數(shù)Fig. 4. Radial distribution function of L-J fluid atwith different temperatures.

3 模擬結(jié)果與討論

3.1 各類弛豫時(shí)間討論

為開展單原子L-J體黏彈性時(shí)間的研究， 計(jì)算了黏彈性特征弛豫時(shí)間、Maxwell弛豫時(shí)間以及原子連通弛豫時(shí)間， 并對(duì)各類黏彈性弛豫時(shí)間進(jìn)行了分析.

3.1.1 黏彈性特征弛豫時(shí)間計(jì)算

通過應(yīng)用(9)和(10)式計(jì)算了T*=0.85—5 ，ρ*=0.85—1，ε=0.97—1 ，σ=0.8—1.3 條件下共 22組單原子L-J體的儲(chǔ)能模量和損耗模量隨頻率的變 化 . 圖 5 為T*=0.9—1.5 ，ρ*=1 ，ε=1 ，σ=1條件下儲(chǔ)能模量G′*和損耗模量G′′*的計(jì)算結(jié)果.由圖 5(a)可以看出， 當(dāng)頻率較小 (0 ＜ω*＜ 10)時(shí)， 儲(chǔ)能模量小于損耗模量， 單原子L-J體主要表現(xiàn)為黏性特征， 儲(chǔ)能模量和損耗模量均隨頻率的上升而增大， 單原子L-J體的彈性和黏性均增強(qiáng);當(dāng)頻率處于中間頻率 (10 ＜ω*＜ 20)時(shí)， 儲(chǔ)能模量和損耗模量接近， 單原子L-J體主要表現(xiàn)出黏彈性特征， 儲(chǔ)能模量隨著頻率的上升逐漸接近并超過損耗模量; 當(dāng)頻率較大時(shí) (ω*＞ 20)， 儲(chǔ)能模量大于損耗模量， 單原子L-J體主要表現(xiàn)為彈性特征， 儲(chǔ)能模量隨著頻率的上升而不斷增大并趨于穩(wěn)定， 單原子L-J體的彈性增強(qiáng)， 損耗模量隨著頻率的上升而不斷減小并趨于穩(wěn)定， 單原子L-J體的黏性減弱. 圖 5(b) 所示為的計(jì)算方法[4]， 物質(zhì)的黏彈性特征弛豫時(shí)間對(duì)應(yīng)于儲(chǔ)能及損耗模量相等時(shí)的頻率， 即:

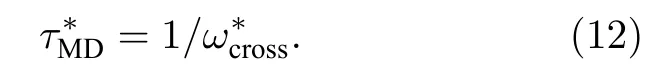
應(yīng)用(12)式， 在儲(chǔ)能模量和損耗模量計(jì)算結(jié)果的基礎(chǔ)上得到單原子L-J體的黏彈性特征弛豫時(shí)間， 結(jié)果示于圖 6. 由圖 6可以看出: 當(dāng)保持不變時(shí) (圖 6(a))， 隨著的上升，不斷減小， 但減小的速度不斷下降; 當(dāng)，保持不變時(shí) (圖 6(b))， 隨著的增大，不斷增大;當(dāng)，保持不變時(shí) (圖 6(c) 和圖 6(d))， 勢(shì)參數(shù)或的增大， 均會(huì)導(dǎo)致的增大.

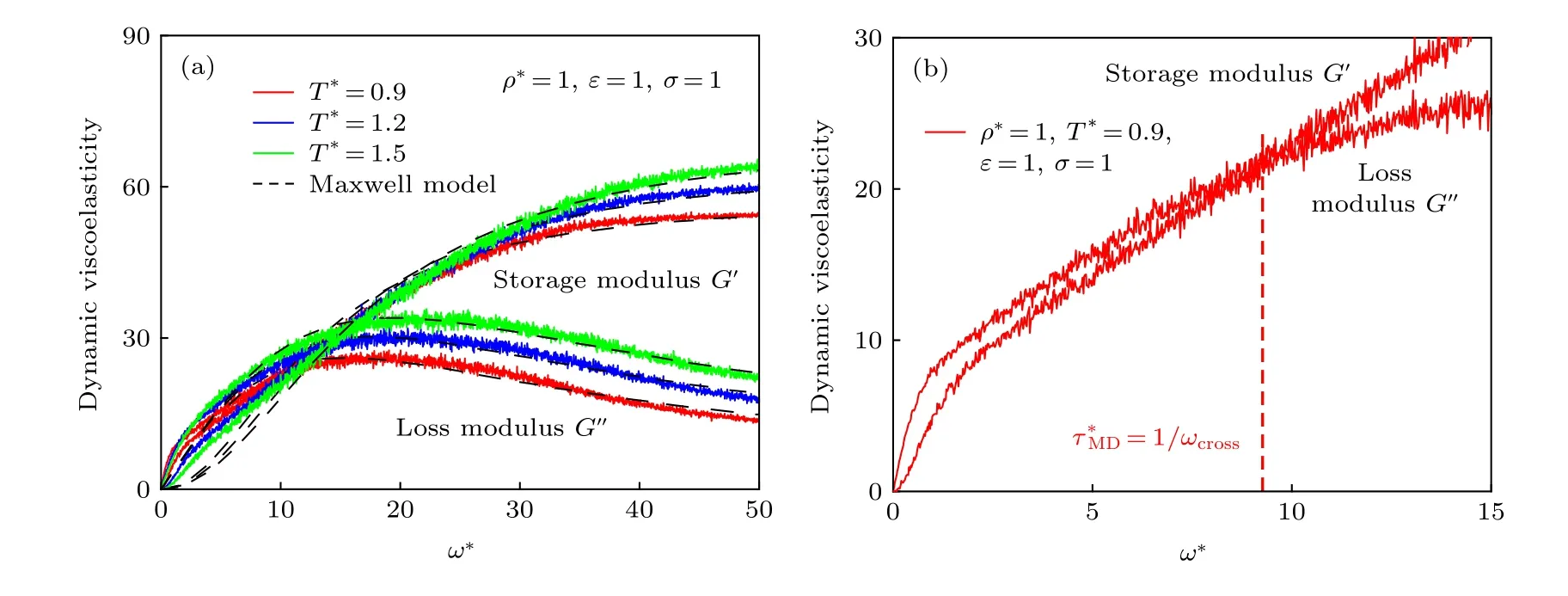
圖 5 儲(chǔ)能模量和損耗模量曲線 (a)不同溫度條件寫的儲(chǔ)能模量和損耗模量曲線; (b)粘彈性特征弛豫時(shí)間Fig. 5. Storage modulus and loss modulus: (a) Storage modulus and loss modulus at different temperatures; (b) viscoelastic characteristic relaxation time .

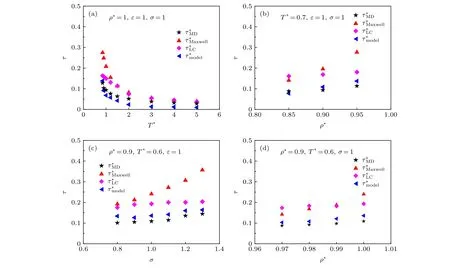
圖 6 不同溫度、密度以及 L-J 勢(shì)參數(shù)下 ， ， ， (a)不同溫度條件; (b)不同密度條件; (c)不同勢(shì)能為 0 時(shí)的原子距離條件; (d)不同勢(shì)能阱深度條件Fig. 6. ， ， ， under different T， ， ε and σ: (a) Different temperatures; (b) different densities; (c) different distances between atoms when potential is 0; (d) different potential well depths.

3.1.2 Maxwell弛豫時(shí)間計(jì)算

通過應(yīng)用(4)式和(6)式計(jì)算了T*=0.85—5 ，ρ*=0.85—1，ε=0.97—1 ，σ=0.8—1.3 條 件 下 單原子L-J體的黏性和無窮大頻率剪切模量G*∞，并計(jì)算各條件下的Maxwell弛豫時(shí)間. Maxwell弛豫時(shí)間的計(jì)算公式[6]為

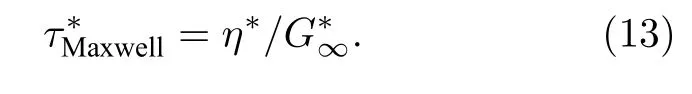
將計(jì)算所得到的各條件下單原子L-J體的Maxwell弛豫時(shí)間與黏彈性特征弛豫時(shí)間進(jìn)行比較， 結(jié)果示于圖6. 由圖6可以看出， 在不同的溫度、密度和勢(shì)參數(shù)條件下，與的變化趨勢(shì)一致; 當(dāng)保持不變時(shí)(圖6(a))，隨著的下降，與的差異逐漸增大， 這說明應(yīng)用Maxwell弛豫時(shí)間表征黏彈性特征弛豫時(shí)間存在一定的局限性; 當(dāng)T*，ε，σ保持不變時(shí)(圖 6(b))， 隨著ρ*的增大，與均逐漸增大， 但axwell 增大的速率更快; 當(dāng)T*，ρ*，ε保持不變時(shí) (圖 6(c))， 隨著的增大，不斷增 大，但與的差異越來越明顯; 當(dāng)T*，ρ*，σ保持不變時(shí) (圖 6(d))， 隨著的增大，與的差異逐漸增大.

上述計(jì)算結(jié)果表明， 當(dāng)溫度較低(T*＜1.5 )時(shí)，與差異明顯， 應(yīng)用 Maxwell弛豫時(shí)間表征單原子L-J體的黏彈性特征弛豫時(shí)間存在一定的局限性.

3.1.3 原子連通弛豫時(shí)間計(jì)算

原子連通數(shù)Nc是指在原子近鄰(徑向分布函數(shù)的第一處谷值位置)范圍內(nèi)的原子數(shù)， 原子連通弛豫時(shí)間τLC[10]是指系統(tǒng)內(nèi)所有原子中發(fā)生一次擴(kuò)散或者匯聚的時(shí)間. 若時(shí)刻原子連通數(shù)為，時(shí)刻總原子連通數(shù)為，則=. 本文基于計(jì)算所得的L-J體原子運(yùn)動(dòng)軌跡， 通過MATLAB程序統(tǒng)計(jì)不同時(shí)刻原子間的距離， 從而分析得出原子的擴(kuò)散或匯聚的時(shí)間.

在本文中， 假設(shè)粒子的擴(kuò)散、匯聚過程是一個(gè)泊松過程， 即每一次粒子的擴(kuò)散、匯聚過程是相互獨(dú)立的. 本文將系統(tǒng)內(nèi)各原子的擴(kuò)散或匯聚時(shí)間進(jìn)行統(tǒng)計(jì)， 圖 7 所示為ρ*=1，T*=1，ε=1 ，σ= 1物性條件下L-J體原子擴(kuò)散或匯聚時(shí)間分布圖， 其他條件下的單原子L-J體原子擴(kuò)散或匯聚時(shí)間分布與該條件下的情況類似. 通過觀察圖7可以發(fā)現(xiàn)， L-J體的原子擴(kuò)散或匯聚時(shí)間分布符合指數(shù)函數(shù)分布的密度函數(shù). 因此， 本文應(yīng)用指數(shù)函數(shù)分布的密度函數(shù)即(14)式去擬合L-J體的原子擴(kuò)散或匯聚時(shí)間分布. 其中， (14)式中的特征時(shí)間即為原子連通弛豫時(shí)間:

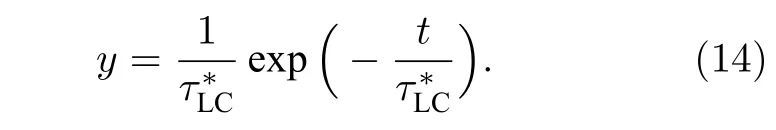
通過應(yīng)用 (14)式得到了T*=0.85—5 ，，ε=0.97—1 ，σ=0.8—1.3 條 件 下 單 原 子L-J體的原子連通弛豫時(shí)間， 并與黏彈性特征弛豫時(shí)間和Maxwell弛豫時(shí)間進(jìn)行比較， 結(jié)果示于圖6. 由圖6可以看出， 在不同的物性參數(shù)和勢(shì)參數(shù)條件下，與具有相同的變化趨勢(shì)， 與相比，對(duì)的預(yù)測(cè)更加準(zhǔn)確;當(dāng)ρ*，ε，σ保持不變時(shí) (圖 6(a))， 隨著T*的下降，axwell 與的差異均逐漸增大， 但與的結(jié)果更加接近; 當(dāng)T*，ε，σ保持不變時(shí) (圖 6(b))，隨著的增大，axwell ，τM*D 均呈現(xiàn)上升趨勢(shì)，但*axwell 增大的速率最快， 而與的差異在減小; 當(dāng)，保持不變時(shí) (圖 6(c))， 隨著的增大，與的差異不斷增大， 而與的差異存在減小的趨勢(shì); 當(dāng)，保持不變時(shí)(圖 6(d))， 隨 著的 增 大 ，與的 結(jié) 果 逐 漸接近.

圖 7 ， ε = 1， σ = 1 條件下 L-J 體原子擴(kuò)散或匯聚時(shí)間分布Fig. 7. Distribution of the dissociation or association time of L-J fluid at ， ε = 1， σ = 1.

與Maxwell弛豫時(shí)間相比， 原子連通弛豫時(shí)間在數(shù)值大小和變化趨勢(shì)上均與黏彈性特征弛豫時(shí)間更加接近， 但原子連通弛豫時(shí)間的計(jì)算需要統(tǒng)計(jì)所有原子在500個(gè)時(shí)間步長(zhǎng)內(nèi)的運(yùn)動(dòng)軌跡， 分析每一個(gè)原子擴(kuò)散或匯聚時(shí)間， 工作量龐大， 計(jì)算過程需要消耗大量的時(shí)間和計(jì)算資源. 因此， 若能通過分析各個(gè)原子周圍的原子排布， 建立一種間接的反映原子擴(kuò)散和匯聚過程的方法， 則可避免在統(tǒng)計(jì)各原子運(yùn)動(dòng)軌跡的過程中消耗大量的時(shí)間和計(jì)算資源.

3.2 預(yù)測(cè)方法及弛豫時(shí)間計(jì)算

在上述計(jì)算過程中， 發(fā)現(xiàn)原子連通弛豫時(shí)間對(duì)黏彈性弛豫時(shí)間的表征更加準(zhǔn)確， 但連通性弛豫時(shí)間的計(jì)算工作量大、耗時(shí)長(zhǎng). 本文在分析每個(gè)原子周圍原子排布的基礎(chǔ)上， 應(yīng)用Kramers逃逸速率理論[29]來描述原子的擴(kuò)散和匯聚過程， 建立了一種新的表征單原子L-J體黏彈性弛豫時(shí)間的方法，避免了統(tǒng)計(jì)所有原子的運(yùn)動(dòng)軌跡時(shí)需要消耗大量時(shí)間和計(jì)算資源.

Kramers逃逸速率理論是常見的描述布朗運(yùn)動(dòng)和化學(xué)反應(yīng)擴(kuò)散的經(jīng)典方法， 圖8所示為Kramers逃逸速率理論示意圖， 其中g(shù)(r)表示的是原子的徑向分布函數(shù)曲線，U(r)表示的是原子的能量變化曲線. 當(dāng)粒子間距離由近處遠(yuǎn)離， 粒子間能量(U(r)曲線)由第一個(gè)谷值點(diǎn)a處上升至能量壁壘b點(diǎn)時(shí)， 發(fā)生擴(kuò)散反應(yīng)， 此時(shí)的能量壁壘為; 而當(dāng)粒子間距離由遠(yuǎn)處靠近， 對(duì)應(yīng)能量(U(r)曲線)由第二個(gè)谷值點(diǎn)c處上升至能量壁壘b點(diǎn)時(shí)， 發(fā)生匯聚反應(yīng)， 其能量壁壘為. 該過程中的能量U可通過徑向分布函數(shù)即曲線獲得:

擴(kuò)散反應(yīng)速率kdiss和kass則可通過能量壁壘Eb及能量曲線波峰(壁壘)、波谷曲率相關(guān)參數(shù)ωa，ωb，ωc和遷移率γ等描述:

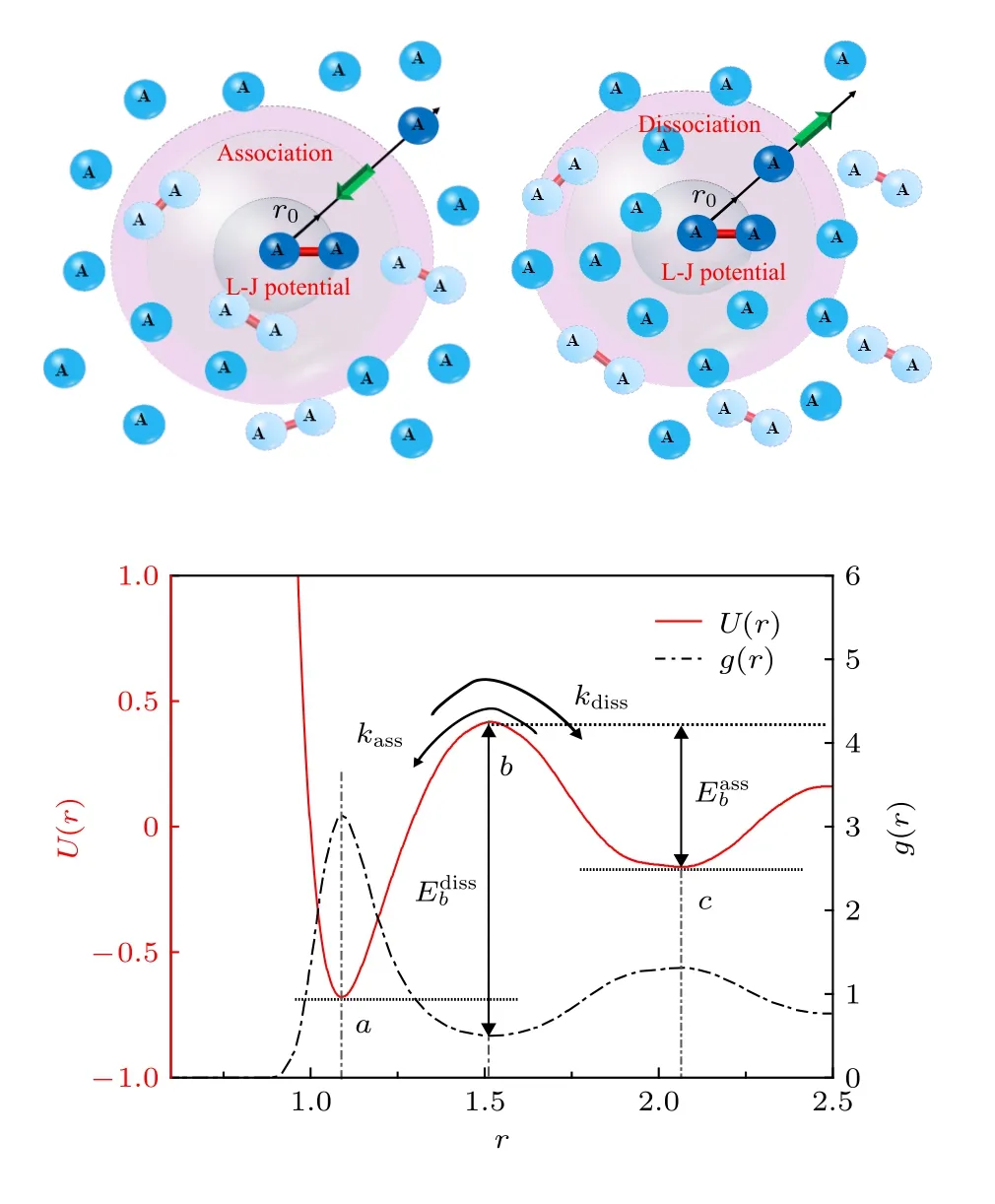
圖 8 Kramers逃逸速率理論示意圖Fig. 8. Schematic diagram of Kramers’ rate theory.

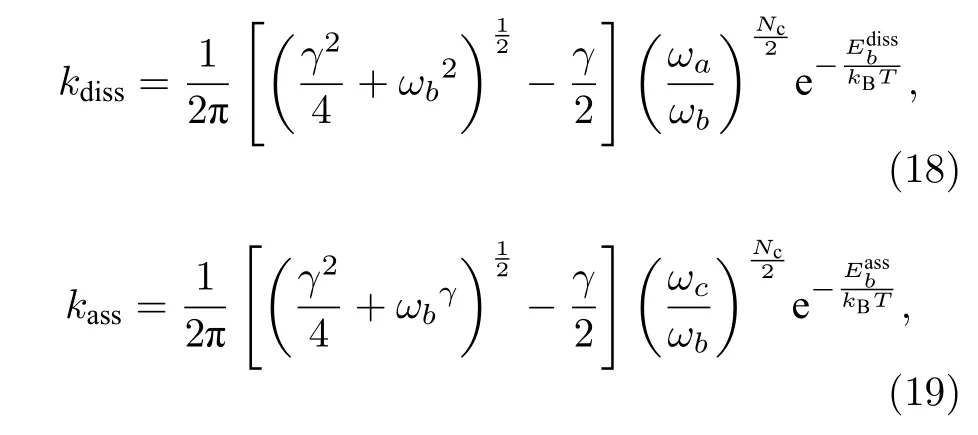
式中Nc為原子連通數(shù)， 可通過本文計(jì)算得到的徑向分布函數(shù)得到;ω表示為

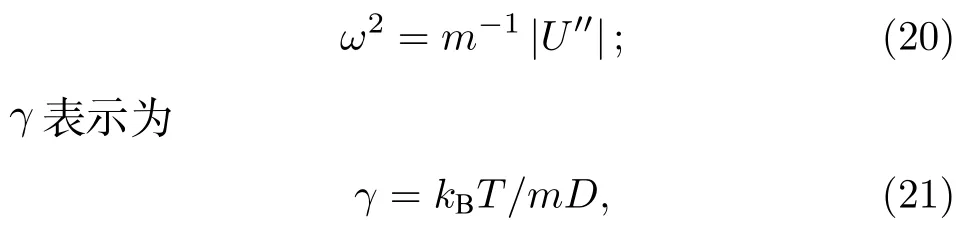
其中D為系統(tǒng)擴(kuò)散系數(shù)，m為單個(gè)原子的質(zhì)量.

假定初始狀態(tài)系統(tǒng)內(nèi)的A原子均兩兩匯聚，形成A—A分子， 即初始條件為

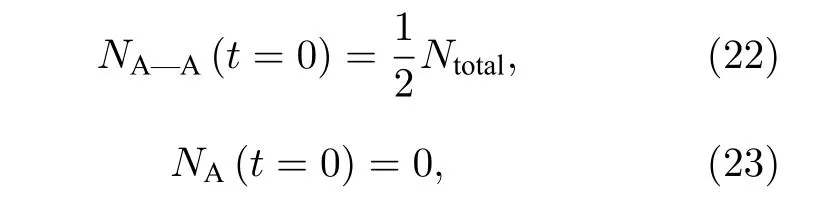
式中N表示系統(tǒng)內(nèi)原子的數(shù)量.

在環(huán)境條件下， L-J體系將發(fā)生A—A分子與A原子的相互轉(zhuǎn)化過程， 反應(yīng)方程式如下:

根據(jù)可逆反應(yīng)機(jī)理， A—A分子與A原子的物質(zhì)的量濃度存在以下關(guān)系:

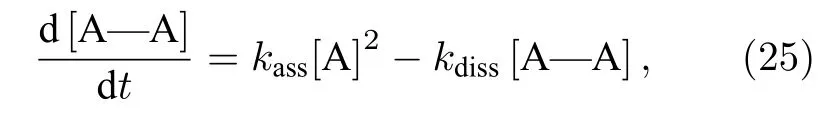
式中[ · ]表示物質(zhì)的量濃度;kass為A原子靠近A—A分子的擴(kuò)散、匯聚過程(圖8)的速率常數(shù);kdiss為A原子遠(yuǎn)離A—A分子的擴(kuò)散分散過程(圖8)的速率常數(shù). 圖9所示為不同溫度、密度、勢(shì)參數(shù)條件下， A原子和A—A分子的數(shù)量隨時(shí)間的變化.

由圖9可知， 在不同的物性條件下， A原子和A—A分子的數(shù)量變化均存在相同的規(guī)律， 隨著時(shí)間的增長(zhǎng)， A原子的數(shù)量不斷增加并趨于一個(gè)定值， A—A分子的數(shù)量不斷降低并趨于一個(gè)定值，A原子和A—A分子的轉(zhuǎn)換過程趨于平衡狀態(tài); 當(dāng)保 持 不 變 時(shí) (圖 9(a))， 隨 著的 上 升 ，A—A分子的耗散速度和A原子的生成速度均增大; 當(dāng)，保持 不 變 時(shí) (圖 9(b))， 隨 著的增大， A—A分子的耗散速度和A原子的生成速度均減小; 當(dāng)，保持不變時(shí) (圖 9(c) 和圖 9(d))，無論的增大還是的增大， 均會(huì)導(dǎo)致A—A分子的耗散速度和A原子的生成速度減小.

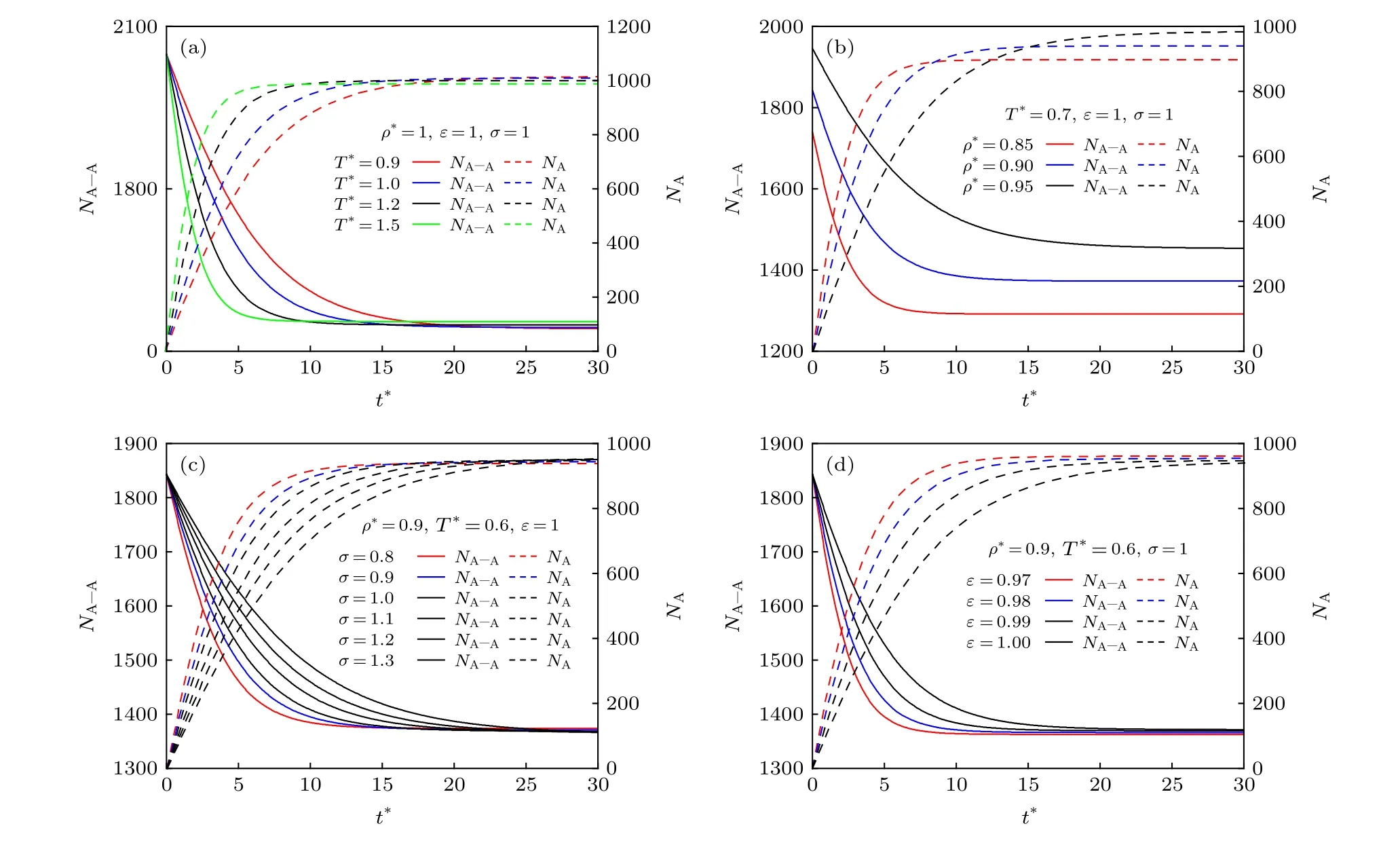
圖 9 A原子和A—A分子的數(shù)量變化曲線 (a)不同溫度條件; (b)不同密度條件; (c)不同勢(shì)能為0時(shí)的原子距離條件; (d)不同勢(shì)能阱深度條件Fig. 9. The quantity curves of A and A—A: (a) Different temperatures; (b) different densities; (c) different distances between atoms when potential is 0; (d) different potential well depths.

進(jìn)一步分析A—A分子的耗散速度和A原子的生成速度的變化與黏彈性的關(guān)系， 應(yīng)用(26)式對(duì)所有條件下單原子L-J體內(nèi)A原子數(shù)量隨時(shí)間的變化進(jìn)行擬合得到擴(kuò)散和匯聚過程的弛豫時(shí)間即為本文提出的預(yù)測(cè)方法弛豫時(shí)間， 結(jié)果示于圖6.

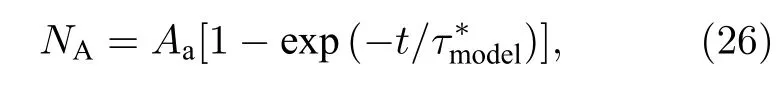
由圖6可以看出， 在不同的物性參數(shù)下， 預(yù)測(cè)方法得到的弛豫時(shí)間與黏彈性特征弛豫時(shí)間具有相同的變化趨勢(shì); 當(dāng)ρ*，ε，σ保持不變時(shí)(圖 6(a))， 隨著T*的下降，axwell 與的差異均逐漸增大， 而與的差異無明顯變化;當(dāng)，ε，σ保持不變時(shí) (圖 6(b))， 隨著ρ*的增大，axwell ，，odel 均呈現(xiàn)上升趨勢(shì)， 但odel與十分接近， 而axwell ，與存在明顯差異; 當(dāng)T*，ρ*，ε保持不變時(shí) (圖 6(c))， 隨著的增大D ，axwell ，，odel 均不斷增大，odel 與的差異最小; 當(dāng)，保持不變時(shí) (圖 6(d))，隨著的增大，與與的結(jié)果最接近.

綜上所述， 與Maxwell弛豫時(shí)間、原子連通弛豫時(shí)間相比， 采用本文提出的預(yù)測(cè)方法得到弛豫時(shí)間與黏彈性特征弛豫時(shí)間在數(shù)值大小和變化趨勢(shì)上均更加接近， 本文所提出的預(yù)測(cè)方法具有一定的準(zhǔn)確性和可靠性.

4 結(jié) 論

本文應(yīng)用平衡態(tài)分子模擬方法計(jì)算了T*=0.85—5，ρ*=0.85—1 ，ε=0.97—1 ，σ=0.8—1.3范圍內(nèi)共22組液固共存態(tài)及液態(tài)的單原子L-J體的黏度(η*)、無限大頻率的剪切模量()、儲(chǔ)能模量(G′*)、損耗模量(G′′*)等黏彈性特性參量， 獲得了黏彈性特征弛豫時(shí)間、Maxwell弛豫時(shí)間、原子連通弛豫時(shí)間， 在此基礎(chǔ)上本文通過分析系統(tǒng)內(nèi)的原子排布情況即徑向分布函數(shù)曲線， 應(yīng)用Kramers逃逸速率理論來描述單原子L-J體內(nèi)原子的擴(kuò)散和匯聚過程， 提出了單原子L-J體黏彈性弛豫時(shí)間的預(yù)測(cè)方法. 本文得到以下結(jié)論:

1) Maxwell弛豫時(shí)間預(yù)測(cè)單原子L-J體黏彈性特征弛豫時(shí)間具有一定的局限性， 低溫情況下預(yù)測(cè)并不準(zhǔn)確; 原子連通弛豫時(shí)間較Maxwell弛豫時(shí)間而言， 其對(duì)單原子L-J體黏彈性特征弛豫時(shí)間的預(yù)測(cè)更為精確， 但在計(jì)算過程中， 需要統(tǒng)計(jì)所有原子在一定時(shí)間步長(zhǎng)內(nèi)的運(yùn)動(dòng)軌跡， 耗費(fèi)大量的時(shí)間和計(jì)算資源.

2) 本文提出的基于Kramer逃逸速率理論的單原子L-J體黏彈性預(yù)測(cè)方法能夠通過徑向分布函數(shù)曲線分析單原子L-J體內(nèi)原子的分離、匯聚過程， 從而實(shí)現(xiàn)對(duì)黏彈性弛豫時(shí)間的預(yù)測(cè). 與Maxwell弛豫時(shí)間和原子連通弛豫時(shí)間相比， 采用預(yù)測(cè)方法得到的弛豫時(shí)間與黏彈性特征弛豫時(shí)間之間的誤差更小， 同時(shí)獲取系統(tǒng)徑向分布函數(shù)曲線的過程不需要耗費(fèi)大量的時(shí)間和資源， 計(jì)算工作量小. 本文提出了一種新的單原子L-J體黏彈性弛豫時(shí)間的預(yù)測(cè)方法， 可為材料黏彈性弛豫時(shí)間的研究提供新的思路.