非晶聚苯乙烯和Pd40Ni10Cu30P20玻璃化轉變中比熱變化的機理和定量研究

姜文龍

(奎克化學(中國)有限公司技術部， 上海 201112)

(2020 年3 月4日收到; 2020 年4 月1日收到修改稿)

玻璃化轉變的本質是現代凝聚態物理中最有趣的問題之一. 有理論認為高分子玻璃化轉變的本質是: 當主鏈原子的擴散運動概率P小于 時， 必有比例不小于1 + 2e3/lnP的主鏈原子擴散運動被凍結. 以該理論的模量溫度公式擬合文獻的聚苯乙烯模量溫度曲線， 得到聚苯乙烯的自由體積膨脹系數值在(0.00045，0.00052)之間. 以此理論為基礎推導得到了玻璃化轉變中的比熱溫度公式: 玻璃化轉變中的材料是橡膠和玻璃的混合物， 其中橡膠的比例是自由體積分數的鏈段中主鏈原子數次方， 總比熱等于兩組分各自的比熱和比例之積的和. 用聚苯乙烯檢驗了該比熱溫度公式， 將計算得到的聚苯乙烯自由體積膨脹系數代入比熱溫度公式， 不需擬合任何參數公式就能夠精準地定量描述聚苯乙烯玻璃化轉變中的比熱溫度關系. 據分析， 聚苯乙烯的玻璃化轉變過程是主鏈原子的擴散運動被激活或者被凍結的過程， 這和非晶合金相關研究結論一致. 以主鏈原子為摩爾計量單元時， 聚苯乙烯轉變中的比熱變化為1.61R (R為氣體常數)， 這和非晶合金玻璃化轉變中比熱變化約為1.5R的規律一致. 這些一致的結論預示非晶合金的玻璃化轉變和聚苯乙烯的玻璃化轉變具有相同的本質， 以此出發， 提出并證明了非晶合金Pd40Ni10Cu30P20和聚苯乙烯的比熱溫度公式是一致的.

1 引 言

玻璃化轉變是指冷凝過程中沒有發生結晶， 而是轉變成非晶態固體的一個過程. 從20世紀初開始凝聚態物理學家就一直在觀察、總結和研究玻璃化轉變過程中材料的狀態和運動的變化.

玻璃轉變過程中會伴隨著熱力學量的變化[1]，最典型的就是在轉變過程中會有一個非常明顯的比熱變化. 玻璃化轉變的比熱變化在比熱溫度曲線上的形狀就像一個臺階， 稱為比熱臺階. 比熱臺階現象存在于所有類型的玻璃化轉變中[2]， 其中尤為特別的是非晶合金的比熱臺階. 實驗發現， 非晶由液體轉變成非晶時比熱的變化均約為1.5R[3-6]，R為氣體常數. 有研究認為原因是金屬液體比非晶金屬多了3個運動自由度[6]， 這3個運動自由度來自于金屬原子的平移擴散運動行為， 金屬液體玻璃化轉變成非晶金屬過程中原子的平移擴散運動被凍結[6].

玻璃化轉變過程會伴隨著弛豫的變化[7，8]， 這反映玻璃化轉變中材料中粒子運動的變化.α弛豫是體系多數粒子大尺度的運動， 主要存在于過冷液體中[9]. 經過玻璃化轉變，α弛豫會在非晶態被凍結[9]， 實質上玻璃化轉變對應過冷液體的弛豫的變化[10]， 玻璃化轉變對應材料中粒子的大規模、大范圍的運動凍結或者激活的過程.

非晶合金比熱臺階的研究表明非晶合金的比熱變化來自于玻璃化轉變中非晶合金的平移擴散運動的變化， 那么其他非晶材料玻璃化轉變中比熱的變化可能也來自于該非晶材料中粒子的大規模、大范圍的運動的變化. 這樣依據玻璃化轉變中粒子的運動變化來定量描述轉變中的比熱變化也是一條可行的研究思路. 本文即沿著這一思路展開研究.

本文選擇了聚苯乙烯作為研究對象， 這是因為目前聚苯乙烯的玻璃化轉變研究較為成熟. 已有文獻詳細闡述了聚苯乙烯在示差掃描量熱法 (DSC)升溫測試過程中的熱流組成[11]. 盧新亞和姜炳政[12]研究了聚苯乙烯的鏈段長度和僵硬因子的關系. 自由體積理論依據Williams-Landel-Ferry方程給出了高分子的自由體積分數隨溫度變化經驗式[13].Turnbull從理論上得到了自由體積分數和運動概率的關系[14]. 因為有了這些研究基礎， 所以研究以聚苯乙烯為入口是一個很好的選擇.

本文想通過研究玻璃化轉變中的運動變化來定量描述玻璃化轉變的比熱變化， 那么研究的核心必然是確定玻璃化轉變中的比熱溫度公式. 因此本文需要找到一個理論能夠推導出符合實驗的比熱溫度公式. 2019年有理論以主鏈原子運動凍結為基礎推導了高分子的模量溫度公式， 并且公式計算結果符合實驗[15]， 本文同樣以主鏈原子的凍結假說為基礎來描述玻璃化轉變中的比熱變化， 以期能得到一個正確的比熱溫度公式.

2 理論基礎

若一個體系的某一運動需要m個變量描述.可以做如下假設:

1) 任一運動狀態均可用一個含m個變量的函數描述;

2)運動是在不同的物理狀態下完成的. 對于其中一個物理狀態， 它的獨立變量是不變的， 記為(a1，a2，···，am)， 那么這個物理狀態下運動對應的函數形式只能是f(a1，a2，···，am) ， 其中a1，a2，···，am相互獨立;

3)所有物理狀態等數學概率.

假設3是依據統計熱力學的基本假設而做出的假設[16].

假設2是一個合理假設， 本文認為， 對于一個具體的物理狀態， 它的物理量(變量)關系必定是確定而且唯一的. 這是本文的根本假設， 這表明僅用一個物理狀態不能表示所有的函數， 即僅用一個物理狀態不能完備描述這一運動， 換而言之這一運動對應的物理狀態應不止一個. 以這3個假設計算得到這一運動對應的物理狀態的個數是一個定值[15]， e為自然常數.

粒子運動存在能壘， 所以對于體系中的任一粒子， 它有兩種運動狀態， 能運動和不能運動. 體系中的不同粒子處于不同的運動狀態， 使得體系處于不同的物理狀態. 根據上面的分析， 體系中物理狀態的總數是不變的， 為， 某一物理狀態要想存在， 它的概率必須大于[15].

基于以上， 數學計算后可以預言存在著這樣的一個相變: 當粒子的某一運動概率P小于 e-e3時，必有比例不小于 1 +e3/lnP的粒子這一運動被凍結[15]. 本文認為玻璃化轉變屬于這一相變[15]. 具體延伸到高分子體系， 對于一個高分子鏈， 確定N個主鏈碳原子構象需要確定2N個粒子的位置(對于主鏈上的雜原子， 如氮氧原子， 可將原子中的電子對作為側基)， 即N個主鏈碳原子的高分子鏈的物理狀態數相當于2N個粒子的系統的物理狀態數，可得: 當高分子中單個主鏈原子擴散運動概率P小于 e-2e3時， 必有一部分主鏈原子的擴散運動會被凍結， 將被凍結的主鏈原子的比例記為G，1+2e3/lnP[15]. 文獻[15]中計算運動概率使用的公式是計算擴散運動的概率公式Turnbull-Cohen方程[14，15]， 這表明主鏈原子被凍結的運動是擴散運動. 結合Turnbull-Cohen方程可得， 當高分子的自由體積分數f小于時， 必有比例不小于的主鏈原子擴散運動被凍結[15]. 本文自由體積分數定義沿用文獻[15]的定義，.結合文獻 [14]的分析，f的數值等于，為自由體積，為占有體積，B是材料常數.

新假說認為鏈段短程擴散運動對模量的貢獻基本是由凍結系數最小的狀態提供的[15]， 并由此計算得到玻璃化轉變中高模量區域非晶乙烯類鏈骨架高分子的模量溫度方程是[15]

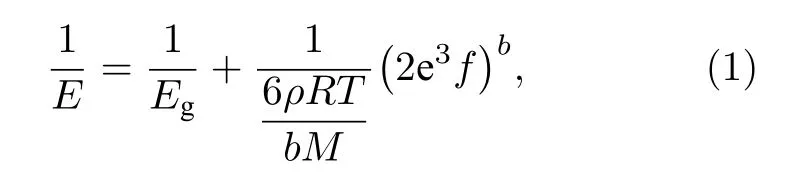
溫度T時自由體積分數f是[13]

乙烯類鏈骨架高分子b滿足[12]

其中E為高分子的拉伸模量，為普彈形變拉伸模量，為高分子的密度，R為氣體常數，T為溫度，b為一個鏈段中的主鏈碳原子數，為僵硬因子(空間位阻參數)[12]，為自由體積膨脹系數，M是一個結構單元的分子量;代表是參考點溫度，為在溫度時高分子拉伸模量， 參考點s的選取原則是約等于 l ogEg-0.5 ，為溫度時的自由體積分數.

由于(1)式和(3)式的原因， 本文只討論乙烯類鏈骨架高分子， 本文中的高分子均特指乙烯類鏈骨架高分子.

3 比熱溫度公式的推導

高分子中獨立運動單元是鏈段， 鏈段是由b個主鏈原子構成的. 當非晶高分子的自由體積分數f小于 1 /(2e3) 時， 擴散運動的主鏈原子的比例不大于. 單個鏈段中的主鏈碳原子數是b， 那么鏈段的短程擴散運動需要這b個主鏈原子一起擴散運動， 那么短程擴散運動的鏈段的比例不大于(2e3f)b. 文獻[15]在推導轉變區內的模量溫度方程時， 假設鏈段的短程擴散運動可認為是由鏈段短程擴散運動比例為的狀態提供的， 得到的結果和實驗符合得很好. 本文繼續沿用這一假設，鏈段短程擴散運動貢獻的比熱可認為是由鏈段短程擴散運動比例為的狀態貢獻的， 這一狀態下的高分子是橡膠和玻璃的混合態， 橡膠(鏈段短程擴散運動激活[17])的比例為玻璃(鏈段短程擴散運動凍結[17])的比例為， 那么轉變區內高分子的比熱為

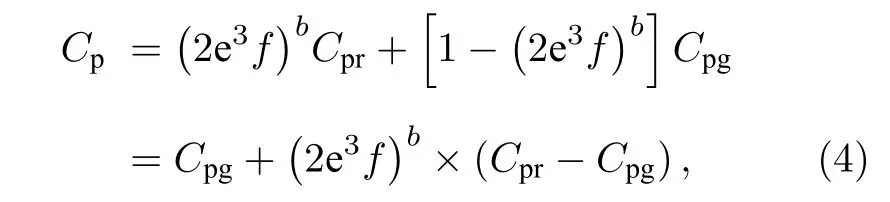
可知， 當T遠小于時， 高分子是玻璃， 此時高分子的比熱; 當T大于時， 高分子是橡膠， 此時高分子的比熱. 根據(6)式可知，時. 即比熱是從時開始變化，對應的是玻璃化轉變中比熱溫度曲線圖上轉變開始的溫度.

4 聚苯乙烯的比熱溫度曲線

4.1 確定自由體積膨脹系數

由(6)式可知， 如要計算模量， 則必須先確定自由體積膨脹系數. 本節的目的是通過擬合聚苯乙烯的模量溫度曲線來確定聚苯乙烯的自由體積膨脹系數的值.

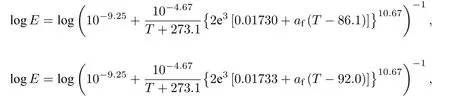
此節檢驗的對數模量范圍約為9.2—8.6 Pa，代入計算可得對應的自由體積范圍為0.013—0.018.結合 (1)—(3)式，隨溫度變化遠比隨溫度變化小， 所以模量隨溫度變化可以認為只與隨溫度變化有關， 擬合就是使得擬合范圍內模量和溫度的關系符合實驗， 也就是使得擬合范圍內和溫度的關系符合實驗.結合(1)—(3)式和擬合分析的過程可知， 擬合就是使得擬合范圍內度的關系符合實驗， 其中不由擬合確定.

4.2 計算比熱溫度曲線

圖2是不同降溫速度下的聚苯乙烯DSC曲線圖， 縱坐標歸一化比熱為實驗計算值. 圖中的曲線取自文獻 [19， 20]， 這些曲線均是實驗實測的， 是聚苯乙烯先降溫后升溫然后通過DSC測量的升溫過程中的歸一化比熱溫度數據， 詳細的測量步驟請查看文獻原文.

從圖2(a)可以看到DSC曲線會有吸熱峰出現， 從圖2(a)可以看到降溫速度越大吸熱峰越小，在降溫速度為100 K/min時吸熱峰已經非常小了.做輔助線如圖2， 可以看到隨著降溫速度的增加，輔助線以上的部分(吸熱峰)越來越小， 可以假設在一個合適的降溫速度下， 輔助線以上的部分會完全消失， 吸熱峰為0. 觀察圖2(a)， 隨著降溫速度的增加， 輔助線以上部分的變化遠遠大于輔助線以下部分的變化. 特別是根據圖2(b)， 可以看到降溫速度由20 K/min變成100 K/min， 輔助線以上的部分變化很大， 而輔助線以下的部分基本不變， 據此可以認為繼續增加降溫速度， 輔助線以上部分會迅速變成零， 而輔助線以下部分會基本不變， 即可以認為這個合適降溫速度下的DSC曲線輔助線以下部分就是100 K/min的DSC曲線在輔助線以下部分， 這個合適降溫速度下的DSC曲線輔助線以上部分就是該溫度區間的輔助線.

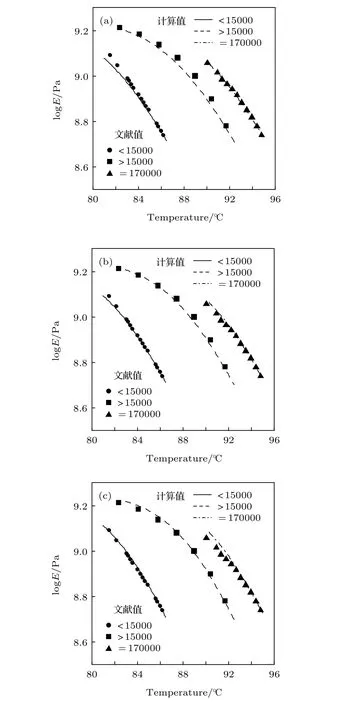
圖 1 以不同 值擬合的不同分子量的聚苯乙烯的模量-溫度曲線(文獻值的原數據取自文獻[17]) (a) a f=0.00045 ;(b) a f=0.00048 ; (c)af=0.00052Fig. 1. Modulus-temperature curves of polystyrene at different molecular weight under different af (The source data of the reference values marked in panel are extracted from Ref. [17]): (a) a f=0.00045 ; (b) a f=0.00048 ; (c)af=0.00052.

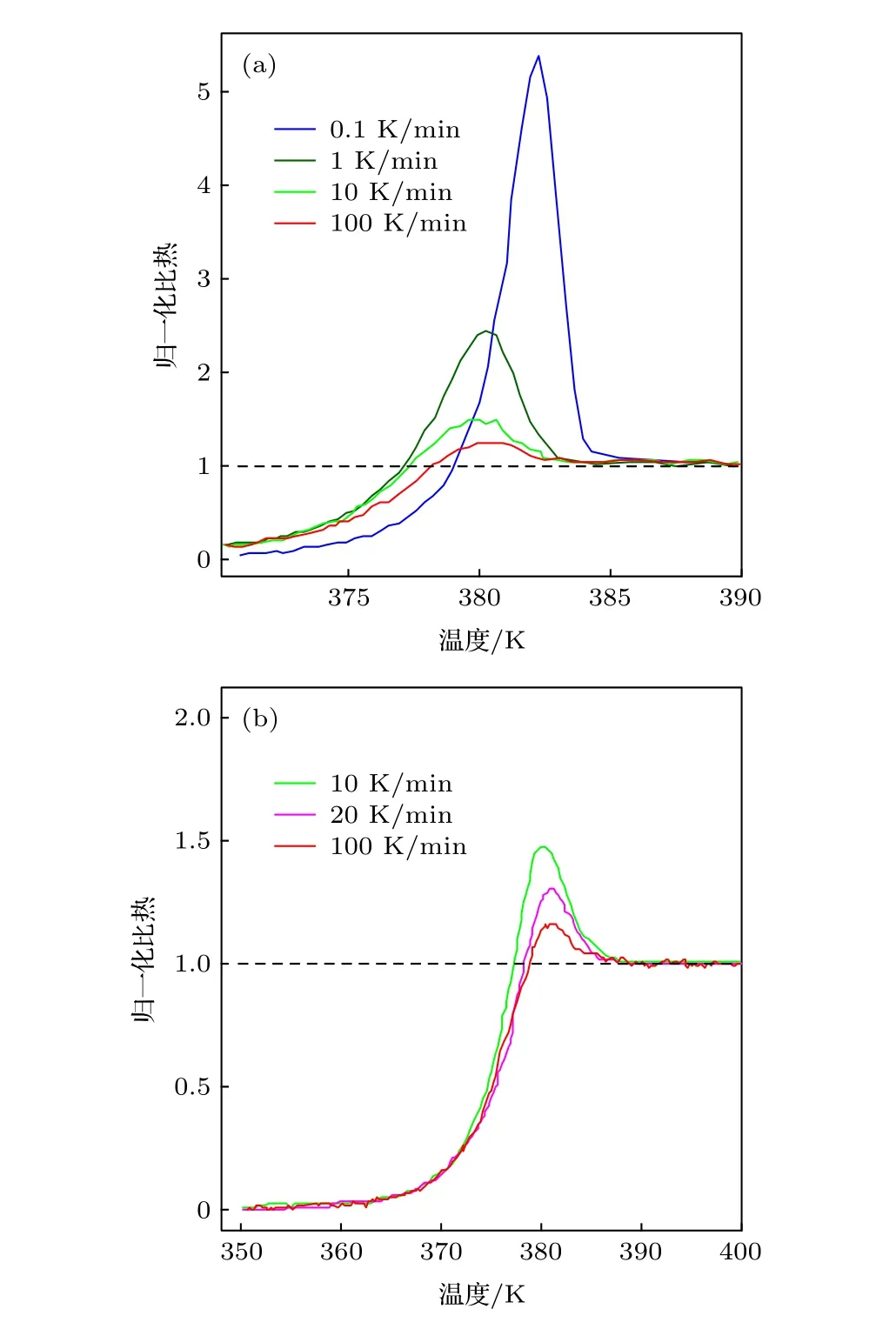
圖 2 不同降溫速度后升溫的聚苯乙烯的DSC測試結果[19，20](a) 0.1， 1， 10， 100 K/min; (b) 10， 20， 100 K/minFig. 2. DSC experimental results of polystyrene recorded after cooling at different cooling rates[19，20]: (a) 0.1， 1， 10，100 K/min; (b) 10， 20， 100 K/min.

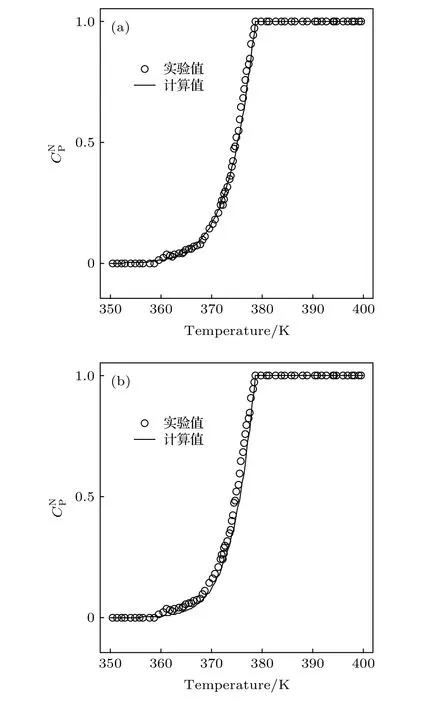
圖 3 不同 值的聚苯乙烯的 的實驗值和計算值(實驗值的原數據取自文獻[20]) (a) = 0.00045; (b) =0.00052Fig. 3. Experimental and predicted of PS at different (The source data of the experimental values marked in panel are extracted from Ref. [20]): (a) = 0.00045; (b) af =0.00052.

根據文獻[11]， 聚合物在DSC升溫測試中的歸一化比熱變化有兩個來源: 一部分是由玻璃化轉變中玻璃組分減少引起的， 另一部分是由滯后焓回復引起的. 升溫過程中， 高分子中玻璃組分隨溫度單調減少， 所以玻璃轉變中的玻璃組分減少是不會產生比熱峰的， 吸熱峰就是由滯后焓的回復引起的. 當高分子是玻璃時， 滯后焓回復引起的歸一化比熱為零[11]; 當高分子是橡膠時， 滯后焓回復引發的歸一化比熱也為零[11]; 那么若玻璃化轉變區內滯后焓引起的歸一化比熱不為零， 則其歸一化比熱溫度曲線上必存在一個峰. 依據這樣分析， 若某DSC測試得到的曲線吸熱峰為零， 那么此條曲線中滯后焓回復引起的歸一化比熱變化也為零， 這條DSC曲線就是材料本身的歸一化比熱溫度曲線. 再結合上述分析， 作聚苯乙烯的歸一化比熱溫度曲線如圖3中圓點線(100 K/min的DSC曲線實驗數據取自文獻[20])， 其縱坐標變量為歸一化比熱的實驗值.的計算公式[19，20]為

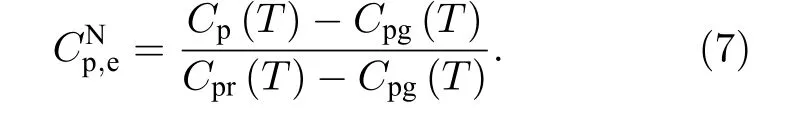
從計算推導過程中可以很清晰地看到， 聚苯乙烯玻璃化轉變開始時(Tc時)自由體積分數為自由體積理論認為， 玻璃化轉變開始時自由體積0.9998， 本文計算得到的聚苯乙烯玻璃化轉變開始時的自由體積分數和自由體積理論認為的玻璃化轉變開始時的自由體積分數是一致的， 這是本文計算正確性的一個佐證.

5 玻璃化轉變中的運動變化

根據第3節， 當聚苯乙烯的自由體積分數f小于時， 擴散運動的主鏈原子的比例不大于，短程擴散運動的鏈段的比例不大于. 結合第4節的分析和圖3可知: 當溫度大于378.7 K時， 聚苯乙烯是橡膠， 沒有鏈段短程擴散運動凍結;計算可得在360 K時聚苯乙烯中短程擴散運動的鏈段的比例不大于0.008， 可以認為360 K時聚苯乙烯中的鏈段短程擴散運動基本已經全部凍結了.聚苯乙烯玻璃化轉變是鏈段短程擴散運動凍結或者激活的過程.

高分子的構型(高分子中由化學鍵所固定的原子在空間的幾何排列)是穩定的， 要改變構型必須經過化學鍵的斷裂和重組. 很明顯， 主鏈原子的擴散運動并不會改變構型. 那么由于構型的限制， 一個主鏈原子擴散運動(一種明顯位移的運動[14])時，該主鏈原子的周圍原子必須隨著這個主鏈原子一起進行一個明顯位移的運動. 橡膠和玻璃在玻璃化轉變區間內高分子鏈已經不能整體平移了， 較小的運動單元(如側基、支鏈和小鏈節)運動的位移不能明顯[13]， 位移能明顯的運動只有鏈段的短程擴散運動. 據此可知高分子鏈段的短程擴散運動的凍結或者激活也會造成主鏈原子的擴散運動的凍結或者激活. 聚苯乙烯玻璃化轉變是鏈段短程擴散運動凍結或者激活的過程， 那么同時， 聚苯乙烯玻璃化轉變也是主鏈原子的擴散運動凍結或者激活的過程.

由文獻[12]可知， 以重復單元作為摩爾量計數單元時， 聚苯乙烯玻璃化轉變的比熱變化是26.8 J·mol—1·K—1. 聚苯乙烯的重復單元是—CH(C6H5)—CH2—， 一個重復單元中有 2個主鏈碳原子， 那么以主鏈原子作為摩爾量計數單元， 玻璃化轉變的比熱變化等于 2 6.8÷2=13.4 J·mol—1·K—1，約等于1.61R. 非晶合金玻璃化轉變比熱變化基本約等于 1.5R[3-6]， 可以看到， 聚苯乙烯也符合這一規律. 非晶合金相關研究認為， 非晶合金原子平移擴散運動的比熱貢獻為1.5R[3]， 非晶合金玻璃化轉變是原子平移擴散運動被激活或者被凍結的過程[3]， 這個結論和本文分析得到的聚苯乙烯玻璃化轉變結論相似. 這些相似預示著聚苯乙烯的玻璃化轉變和非晶合金的玻璃化轉變有著同樣的本質， 且聚苯乙烯玻璃化轉變的單元是主鏈原子， 而不是鏈段.

6 Pd40Ni10Cu30P20的比熱溫度公式

第5節的分析表明非晶合金的玻璃化轉變和聚苯乙烯的玻璃化轉變可能有著同樣的本質，那么它們的比熱公式極有可能是通用的， 所以本節用聚苯乙烯的比熱溫度公式來擬合非晶合金Pd40Ni10Cu30P20的比熱溫度曲線.

此節討論的是非晶合金Pd40Ni10Cu30P20在玻璃化轉變中的比熱溫度曲線， 數據來源于文獻[4]的圖2(b).

Pd40Ni10Cu30P20是過冷液體時， 其在溫度T時的比熱是-0.0007T+0.325+A， 而 Pd40Ni10Cu30P20是玻璃時， 其在溫度T時的比熱是0.0001T-0.349+A，A為一個固定值. 取吸熱峰的最高峰值溫度 587 K 作為玻璃化轉變溫度， 那么時過冷液體和玻璃的比熱差即比熱臺階為0.204 J·g—1·K—1. Pd40Ni10Cu30P20的 摩 爾 質 量 是7368 g/mol， 以單原子作為摩爾量計數單元，等于 0.204×7368÷100=15.03 J·mol—1·K—1， 約等于1.81R， 符合“非晶合金的比熱臺階基本等于1.5R”的規律. 根據第5節的分析， 以主鏈原子作為摩爾量計數單元， 聚苯乙烯的比熱臺階基本等于1.5R. 依據這樣的分析， Pd40Ni10Cu30P20中的單原子等價于聚苯乙烯中的主鏈原子， 這樣就可以把非晶合金Pd40Ni10Cu30P20當作非晶高分子來處理了， 比熱按照(6)式計算，取溫度T時Pd40Ni10Cu30P20是過冷液體時的比熱.

按照第4.2節的方式處理文獻[4]的圖2(b)，可以由降溫速率為80 K/min的實驗曲線得到Pd40Ni10Cu30P20的比熱溫度曲線， 如圖4(a)圓點曲線. 可知等于581.68 K. 從曲線上選取兩點(579.21， —0.1372 +A) 和 (575.74， —0.1927 +A)(圖 4(a)黑點)， 代入 (6)式計算可得:af=0.00027 ，b= 11.57. 計算得到曲線如圖4(a)實線所示， 擬合曲線和實驗數據非常符合.

再從曲線上選取兩點 (579.21， —0.1372 +A)和 (571.04， —0.2416 +A) (如圖 4(b)黑點所示)，代入(6)式計算可得:af=0.00043，b=7.20 . 計算得到曲線如圖4(b)實線所示， 可以看到由這組擬合參數得到的曲線也和實驗數據非常符合.

兩次擬合說明使用(6)式和兩個點就可以擬合得到一條非常符合實驗數據的曲線， (6)式對于Pd40Ni10Cu30P20是適用的. 但是通過兩次擬合也可知取不同點計算得到的是不一樣的， 本文認為原因是實驗數據的精度不夠、實驗數據和真實值有偏差， 所以依據實驗數據計算得到的和材料真實的也是有偏差的. 不過可以看到， 取不同點計算得到的差別很大， 所以依據實驗數據求材料的存在著理論的可能， 實際操作上對實驗數據的精度要求非常高. 兩次擬合的點是任意取的， 如有興趣還可以再任選兩點進行擬合， 擬合結果也支持以上結論.

圖 4 Pd40Ni10Cu30P20的比熱溫度曲線(文獻值的原數據取自文獻 [4]) (a) af = 0.00027， b = 11.57; (b) af = 0.00043，b = 7.20Fig. 4. Specific heat-temperature curves of Pd40Ni10Cu30P20(The source data of the reference values marked in panel are extracted from Ref. [4]): (a) af = 0.00027， b = 11.57; (b) af =0.00043， b = 7.20.

7 結 論

本文的所有結論都是通過比熱溫度公式(6)定量分析實驗后得到的， 圖3和圖4也證明了(6)式的定量分析精度非常高.

1)本文對聚苯乙烯玻璃化轉變的定量計算和分析支持: 聚苯乙烯玻璃化轉變的判據是當聚苯乙烯中單個主鏈原子擴散運動概率P小于時必有比例不小于的主鏈碳原子的擴散運動被凍結.

2)本文的研究表明聚苯乙烯的玻璃化轉變是主鏈原子擴散運動凍結或者激活的過程， 這個結論和非晶合金相關研究結論一致， 之后又證明非晶合金Pd40Ni10Cu30P20和聚苯乙烯在玻璃化轉變中比熱溫度公式是一致的， 這些研究支持“非晶合金的玻璃化轉變和聚苯乙烯的玻璃化轉變有著同樣的本質”這一結論. 結合結論1， 本文認為非晶合金的玻璃化轉變判據是當非晶合金中原子擴散運動的概率P小于時， 則必有比例不小于的原子擴散運動被凍結. 這個判據對開發新的非晶合金有指導意義， 對開發新的非晶材料有啟示意義.

3)根據第6節的分析， 對于非晶合金，b值很可能大于1.b值對于非晶合金是一個非常重要的參數，b值大于1代表著過冷非晶合金液體的運動單元不是金屬原子， 而是高分子鏈段一樣的金屬原子鏈段. 如果可以進一步研究b值和材料特性、溫度之間的關系， 那么可能會對過冷液體的形成原因和運動規律有更為深刻的認識.