傾斜Poiseuille-Rayleigh-Bénard流動的對流分區與動力學特性*

寧利中 張珂 寧碧波 劉爽 田偉利

1) (西安理工大學水利水電學院， 西安 710048)

2) (嘉興學院建筑工程學院， 嘉興 314001)

3) (上海大學建筑系， 上海 200444)

(2019 年12 月21日收到; 2020 年3 月25日收到修改稿)

利用流體力學基本方程組的數值模擬， 探討了具有通過流動的傾斜腔體中普朗特數Pr = 6.99的流體的對流分區與動力學特性. 結果表明， 對于相對瑞利數r = 9， 在通過流動雷諾數Re = 1.5時， 隨著腔體傾斜角θ的增加， 系統出現均勻行波對流、非均勻行波對流以及單對流圈斑圖; 在通過流動雷諾數Re = 12.5時， 隨著腔體傾斜角θ的增加， 系統出現局部行波對流、平行流及局部單對流圈斑圖; 進一步， 對通過流動雷諾數Re和腔體傾斜角θ的不同組合情況的數值模擬， 發現在通過流動雷諾數Re和腔體傾斜角θ構成的平面上，具有通過流動的傾斜腔體中的對流可以分成前述六種斑圖區域， 即均勻行波對流區、非均勻行波對流區、單對流圈區、局部行波對流區、平行流區及局部單對流圈區. 研究了不同對流區域對流最大垂直流速wmax和努塞爾數Nu隨著時間的變化特性. 探討了不同對流區域對流振幅A和努塞爾數Nu隨著腔體傾斜角θ變化的動力學特性.

1 引 言

自從20世紀初Henri Bénard首先對底部加熱流體層對流進行實驗， Lord Rayleigh首先進行小擾動理論分析以來， Rayleigh-Bénard對流問題一直受到許多研究者的廣泛關注[1，2]. 文獻[1， 2]就Rayleigh-Bénard對流問題的研究進展進行過綜述. 關于Rayleigh-Bénard對流問題的研究方法分為實驗研究、理論分析以及數值模擬. 最初， 人們通過實驗及理論分析的方法進行研究. 隨著計算機的發展， 數值模擬分析研究獲得了很大進展. 基于對流振幅方程組的模擬具有計算時間少又能定性揭示對流特性的特點[3，4]. 由于Rayleigh-Bénard對流現象可以精確地由流體力學的連續方程、動量方程及能量方程來描述， 因此， 基于流體力學方程組的數值模擬引起了廣泛的研究興趣[5-16]. 已經揭示了行波[5-7]、局部行波[8-12]、振動對流[9]、行波中的缺陷結構[6，7，12，13]、擺動行波[14，15]及對傳波[16]等對流結構或者現象， 取得了豐富的成果. 在對經典Rayleigh-Bénard對流問題研究的基礎上， 對水平腔體的一側施加水平流動[17-19]， 研究水平流動對Rayleigh-Bénard對流問題的影響. 已經發現了對流發生的附近的線性特性[17]， 局部行波的周期性[18]，對流斑圖的分區特性及斑圖成長特性[19]等一些新的對流結構. 如果對于經典Rayleigh-Bénard對流問題， 考慮腔體傾斜時[20-25]， 研究獲得了一些新的對流特性， 如缺陷湍流， 對流層的雙穩定性與競爭，不同普朗特數情況下的對流斑圖、分區及臨界條件等. 本文進一步在考慮腔體傾斜的同時， 也考慮通過流動對Rayleigh-Bénard對流問題的影響， 試圖獲得一些新的對流結構或者對流現象.

本文利用流體力學基本方程組的數值模擬， 探討了具有通過流動的傾斜腔體中普朗特數Pr=6.99的流體的對流分區與動力學特性. 對不同通過流動雷諾數和腔體傾斜角的組合情況的數值模擬， 發現在通過流動雷諾數和腔體傾斜角構成的平面上， 具有通過流動的傾斜腔體中的對流可以分成六種斑圖區域， 即均勻行波對流區、非均勻行波對流區、單對流圈區、局部行波對流區、平行流區及局部單對流圈區. 這是本文模型不同于以前模型的最大特點. 不同對流區域對流最大垂直流速和努塞爾數隨著時間的變化具有不同特性. 不同對流區域對流振幅A和努塞爾數隨著腔體傾斜角的變化也具有不同動力學規律.

2 數學物理模型

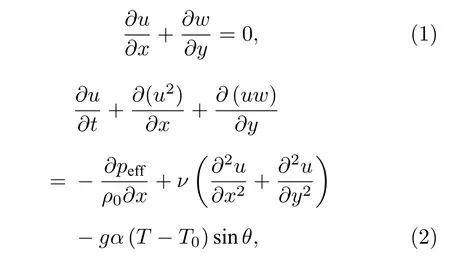
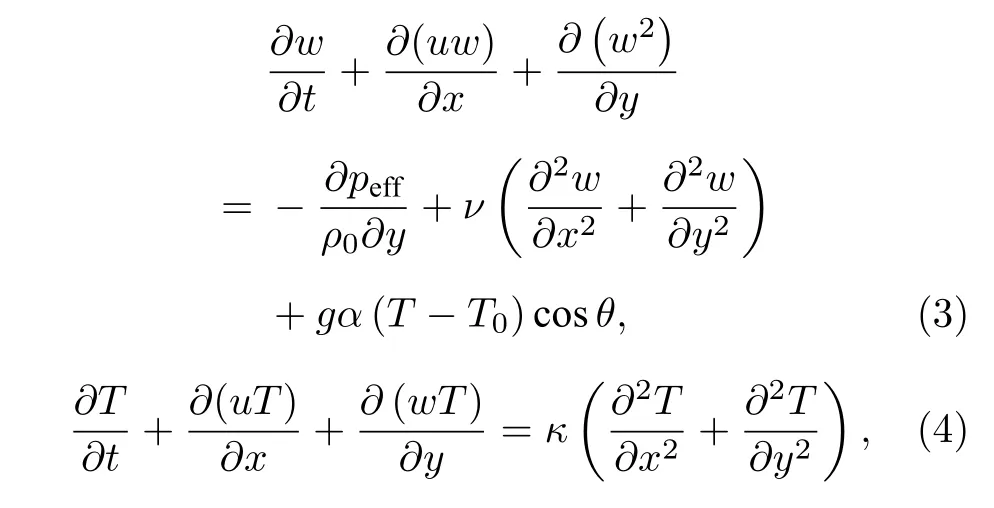
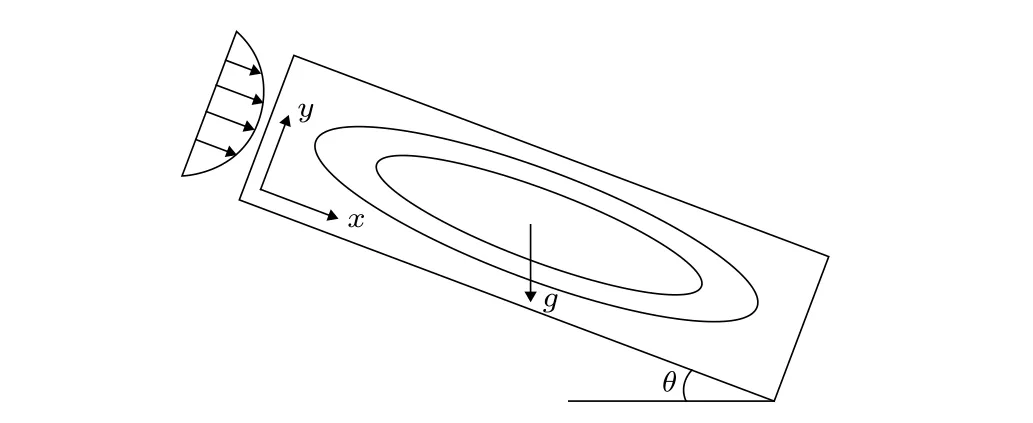
圖 1 傾斜腔體的流動示意圖Fig. 1. Flow diagram in inclined cavity.

在數值計算中， 利用有限容積法離散了控制力學方程組， Simple算法用于求解速度-壓力耦合方程. 擴散項采用中心差分格式， 對流項采用迎風格式， 時間項采用一階隱式格式離散. 采用均勻交錯網格系統. 數值模擬的可靠性和正確性可以由文獻[26]的實例證明. 由于文獻[27]對與的網格進行了計算， 發現計算結果幾乎相同， 誤差很小. 所以采用的網格進行模擬， 時間步長采用s.

討論中采用量綱歸一化參數描述腔體體形， 坐標為X=x/d，Y=y/d， 長高比為Γ=Lx/d. 對流系統可以由瑞利數(為了方便， 使用相對瑞利數r=Ra/Rac， 其中Rac=1708 )， 普朗特數Pr=， 表征進口流動的雷諾數及傾斜腔體的傾角來控制.

本 文 采 用T0=293.15 K ，Pr=6.99 的 流 體 .長高比Γ=20 .

3 對流分區與動力學特性

3.1 不同的對流斑圖結構

對于具有通過流動的傾斜腔體中Pr=6.99 的對流， 當給定相對瑞利數r=9 時， 不同的通過流動雷諾數和不同的傾斜角度組合時， 系統出現六種不同的對流斑圖.

3.1.1 均勻行波對流

當Re=1.5 并且時， 出現均勻行波對流結構， 如圖2所示. 圖2(a)為腔體中的溫度場，可以看出， 溫度場上升羽流和下降羽流間隔出現，羽流以垂直線為對稱; 在腔體長度方向上均勻分布. 圖2(b)為腔體中的流線分布， 在向上彎曲的通過流線的下部或者向下彎曲的通過流線的上部出現封閉的流線圈， 流線圈均勻分布. 溫度場下降羽流的位置和兩個流線圈之間的下降流位置相對應;溫度場上升羽流的位置和兩個流線圈之間的上升流位置相對應. 腔體中共有23個流線圈， 它的波數為k=23π/20=3.61 . 圖2(c)為腔體中011范圍內的速度矢量場. 在向上彎曲的通過流線的下部的矢量場即下壁面附近的矢量場是順時針方向; 在向下彎曲的通過流線的上部的矢量場即上壁面附近的矢量場是逆時針方向. 這一對具有不同旋轉方向的對流圈沿腔體長度方向上交替出現. 在對流圈的左側如果是箭頭向下的下降流， 在對流圈的右側必然是箭頭向上的上升流. 沿腔體長度方向上， 可以清楚地看出， 上升流和下降流交替地出現.在上升流和下降流處垂直速度較大， 對流圈的上下部水平速度較大. 對流圈的中心部位速度較小. 由圖2可以看出， 溫度場、流線及速度矢量場都是均勻分布并整體上向一個方向流動， 類似于Rayleigh-Bénard-Poiseuille 流動中出現的行波， 因此稱其為均勻行波.

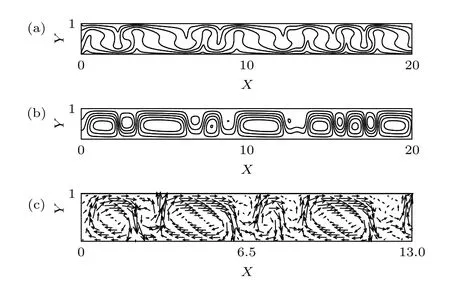
圖 3 和 時的非均勻行波對流 (a) 溫度; (b)流線; (c)速度矢量Fig. 3. Non-uniform traveling wave convection atand : (a) Temperature; (b) streamlines; (c) velocity vector.

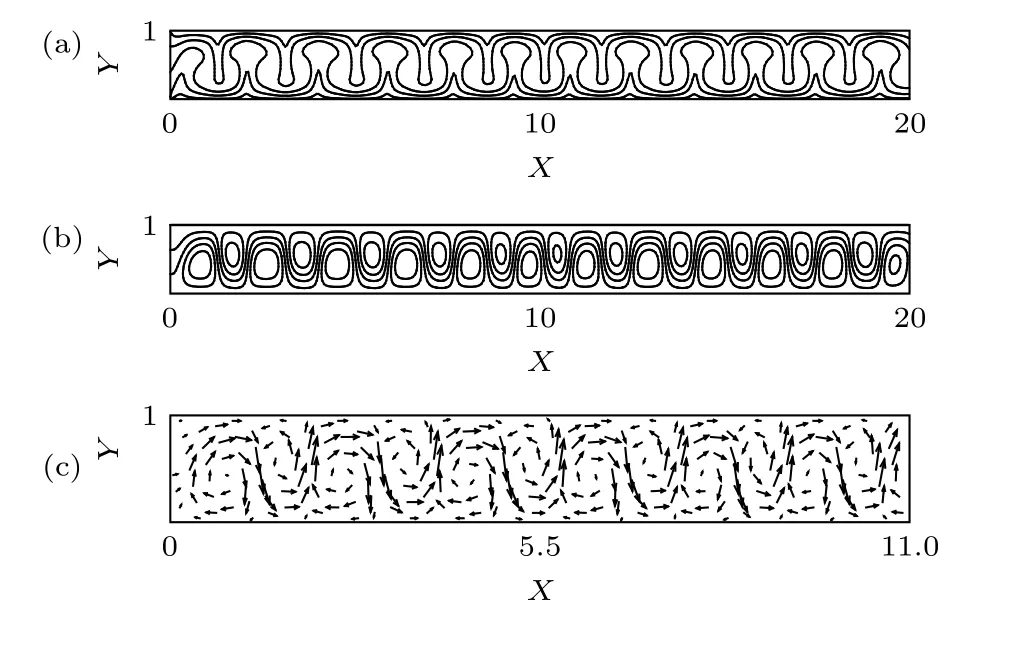
圖 2 且 時的均勻行波對流 (a) 溫度;(b)流線; (c)速度矢量Fig. 2. Uniform traveling wave convection at and: (a) Temperature; (b) streamlines; (c) velocity vector.

3.1.2 非均勻行波對流

3.1.3 單對流圈斑圖

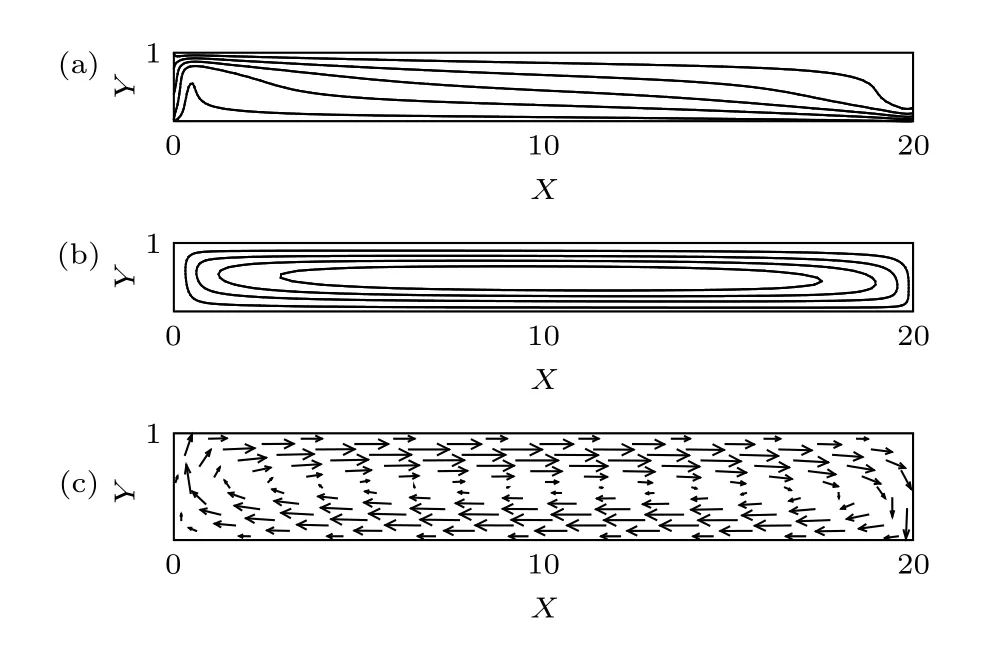
圖 4 和 時 的 單 對 流 圈 (a) 溫 度 ;(b)流線; (c)速度矢量Fig. 4. Single roll convection at and :(a) Temperature; (b) streamlines; (c) velocity vector.

3.1.4 局部行波對流斑圖

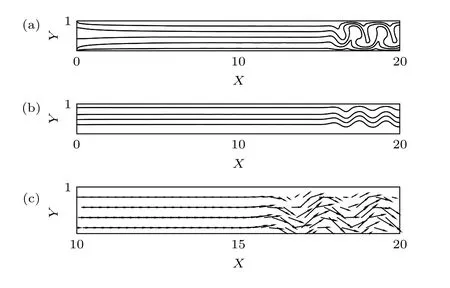
圖 5 R e=12.5 和 時的局部行波對流 (a) 溫度;(b)流線; (c)速度矢量Fig. 5. Localized traveling wave convection atRe=12.5 and : (a) Temperature; (b) streamlines; (c) velocity vector.

3.1.5 平行流斑圖

保持雷諾數為Re=12.5 ， 增加傾斜角到θ=10°時， 系統出現平行流斑圖， 如圖 6所示. 可以看出， 0 ≤X≤20 范圍內的溫度等值線和流線與10≤X≤15范圍內的速度矢量圖都是一些平行于上下壁面的直線， 故稱其為平行流.

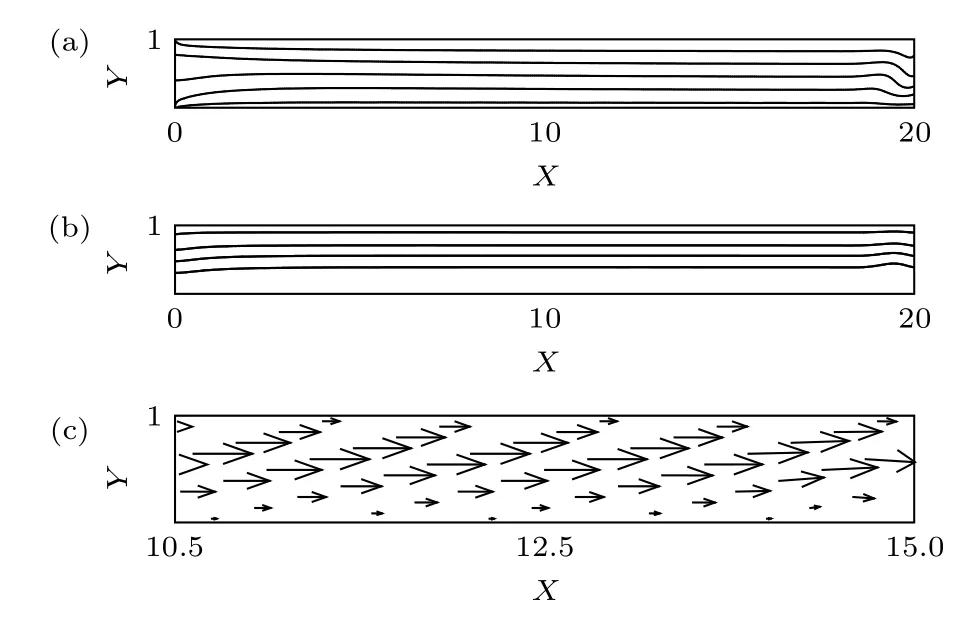
圖 6 和 時的平行流動 (a) 溫度;(b)流線; (c)速度矢量Fig. 6. Parallel flows at and : (a) Temperature; (b) streamlines; (c) velocity vector.

3.1.6 局部單對流圈斑圖

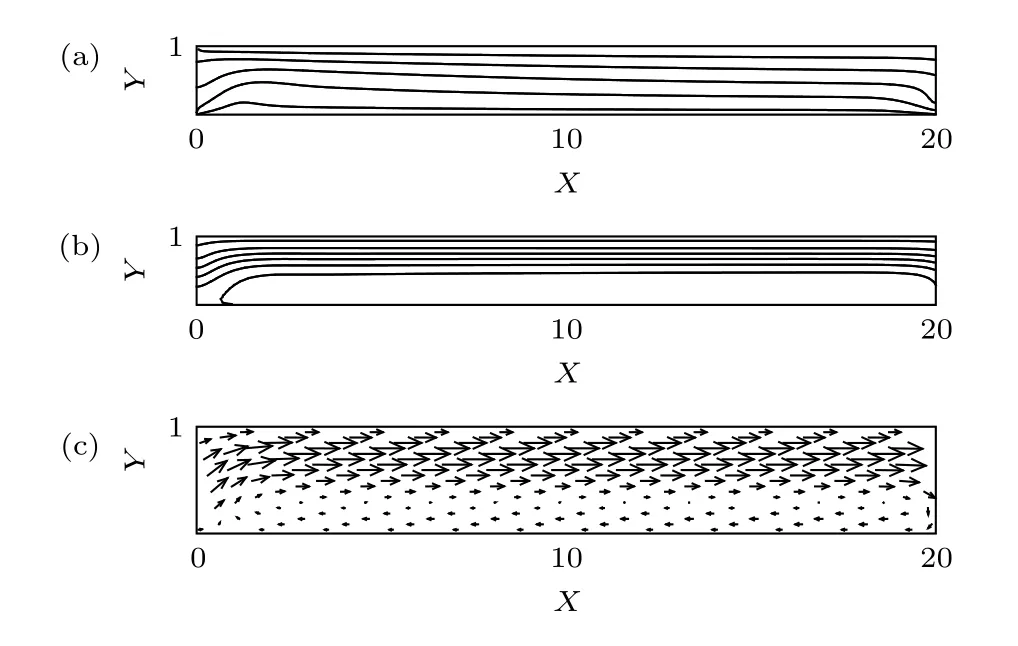
圖 7 R e=12.5 和 θ =45° 時的局部單對流圈 (a) 溫度;(b)流線; (c)速度矢量Fig. 7. Localized single roll convection at and: (a) Temperature; (b) streamlines; (c) velocity vector.

3.1.7 對流垂直最大流速隨著時間的變化特性

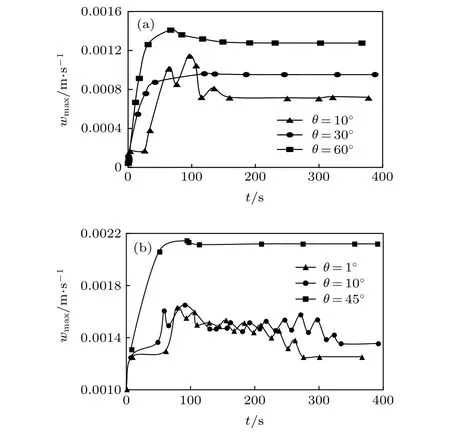
圖 8 不同對流結構的最大垂直流速的時間演化 (a) Re =1.5; (b) Re = 12.5Fig. 8. Time evolution of maximum vertical velocity in different convection structures: (a) Re = 1.5; (b) Re = 12.5.

3.1.8 努塞爾數Nu隨著時間的變化特性

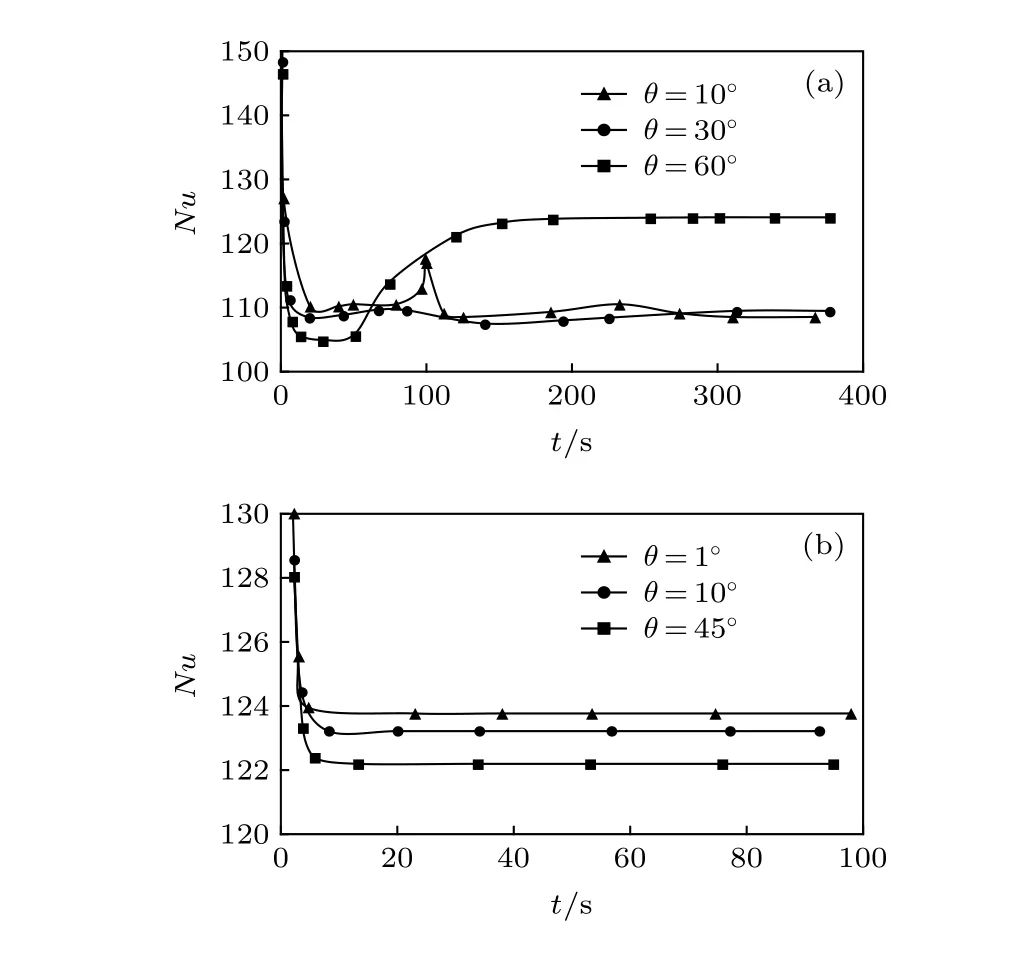
圖 9 不同對流結構的努塞爾數的時間演化 (a) Re =1.5; (b) Re = 12.5Fig. 9. Time evolution of Nusselt number in different convection structures: (a) Re = 1.5; (b) Re = 12.5.

圖9(b)是相對瑞利數r=9 ， 雷諾數Re=12.5及傾斜角分別為θ=1°， 1 0°， 4 5°時對應的局部行波對流、平行流及局部單對流圈斑圖的努塞爾數Nu隨著時間的變化. 三種情況下， 努塞爾數Nu隨著時間增加而減小， 在t=10 s左右達到穩定. 與小雷諾數情況下相反， 努塞爾數隨著傾斜角的增加而減小.

3.2 對流斑圖的分區

對前述的六種對流斑圖進行了大量的數值模擬后， 發現當r=9 時在傾斜角與雷諾數平面上可以劃分為6個不同的區域， 如圖10所示. 對于較小的雷諾數， 當傾斜角較小時， 由于傾斜角對對流的影響微乎其微， 在腔體長度方向冷面上的重力分力和熱面上浮力都很小， 可以忽略， 系統出現的是類似水平腔體情況下的均勻行波對流;隨著傾斜角的增加， 在腔體長度方向冷面上的重力分力和熱面上浮力都已經發揮作用， 隨著兩個方向浮力作用的競爭， 系統中的均勻行波對流轉變成非均勻行波對流; 隨著傾斜角的進一步增加， 在腔體長度方向冷面上的重力分力和熱面上浮力明顯加強， 起到控制作用， 系統過渡到單對流圈斑圖.對于雷諾數Re=10 附近的情況， 當傾斜角較小時， 由于傾斜角對對流的影響微不足道， 在腔體長度方向冷面上的重力分力和熱面上浮力很小， 其影響可以忽略， 系統出現的是類似水平腔體情況下的局部行波對流; 隨著傾斜角的增加， 在腔體長度方向冷面上的重力分力和熱面上浮力變得明顯，與雷諾數的綜合作用結果使系統轉化成局部單對流圈斑圖. 對于雷諾數的情況， 雷諾數的影響明顯， 起了控制作用， 對于傾斜角θ約小于的情況， 系統出現的都是平行流斑圖. 在傾斜角θ約大于時， 形成平行流動的臨界雷諾數幾乎線性變大.

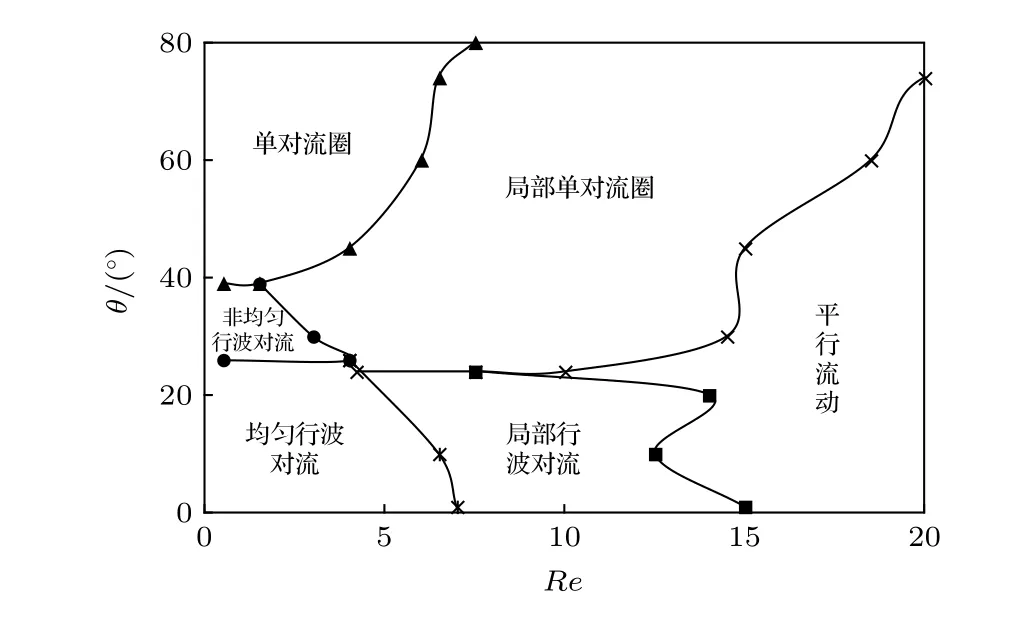
圖 10 不同對流斑圖在傾斜角度 -雷諾數 平面上的分區Fig. 10. Partition of different convective patterns in the plane - .

3.3 對流斑圖的動力學特性

3.3.1 對流振幅的特性

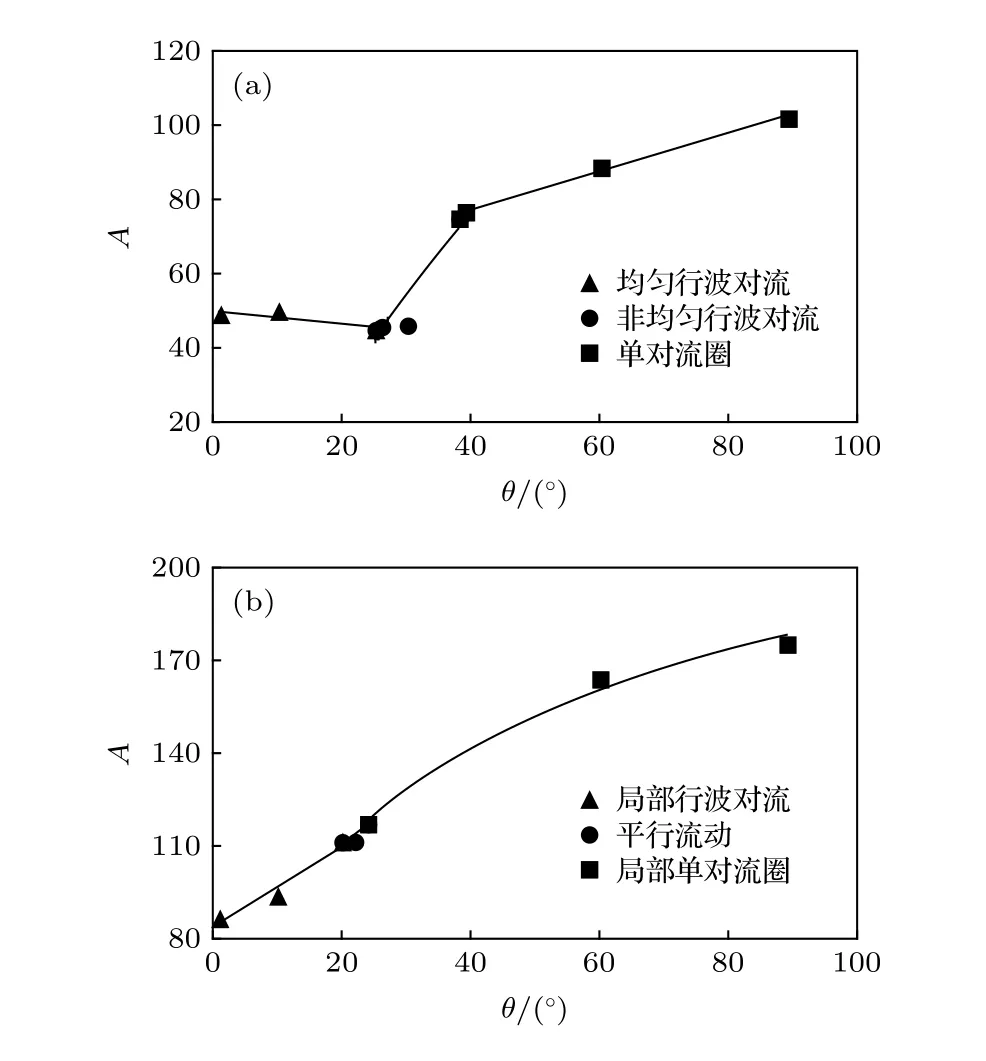
圖 11 不同對流結構時A隨著 的變化 (a) Re = 1.5;(b) Re = 12.5Fig. 11. Variation of A in different convection structures with : (a) Re = 1.5; (b) Re = 12.5.

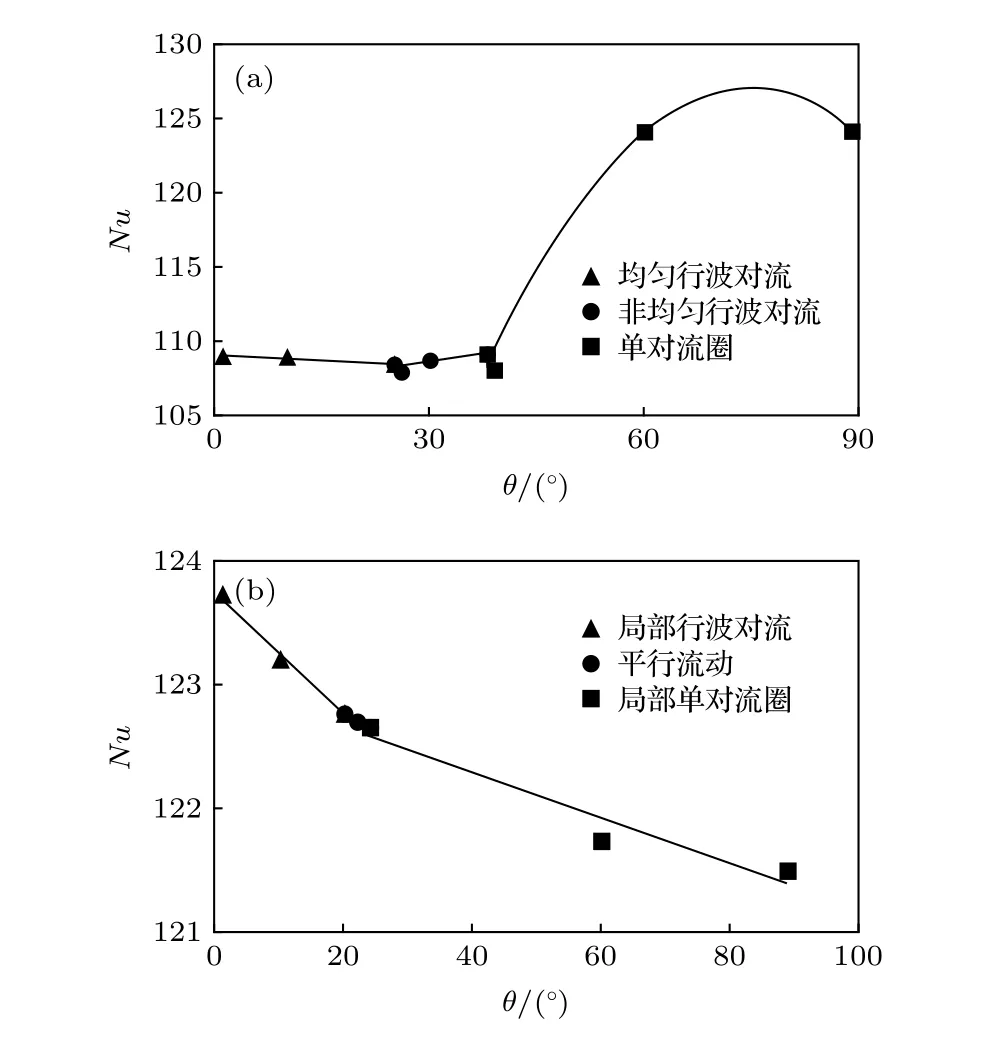
圖 12 不同對流結構時 隨著 的變化 (a) Re = 1.5;(b) Re = 12.5Fig. 12. Variation of in different convection structures with : (a) Re = 1.5; (b) Re = 12.5.

3.3.2 努塞爾數的特性

4 結 論

利用流體力學基本方程組的數值模擬， 探討了具有通過流動的傾斜腔體中普朗特數的流體的對流分區與動力學特性. 可以得出以下結論.

3)最大振幅A隨著傾斜角的增加而增加， 不同對流斑圖區變化規律不同. 努塞爾數隨著傾斜角的變化特性說明， 均勻行波對流與非均勻行波對流時努塞爾數隨著傾斜角的變化幾乎不發生變化. 單對流圈斑圖， 努塞爾數隨著傾斜角的增加而增加. 局部行波對流、平行流及局部單對流圈斑圖的努塞爾數隨著傾斜角的增加而減小.