二元一次方程組概念教學與學生核心素養培養
林向群
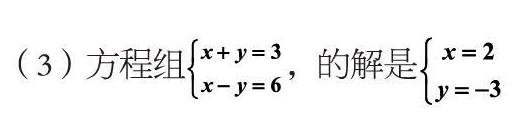
對學生數學核心素養的培養是教育改革的目標,如何在平時的教學中實現這一目標,或者說如何在教學中如何體現這一目標,是值得研究的。
一、初中數學核心素養的涵義
對于初中階段的數學核心素養內容,馬云鵬教授認為,應當是以下“核心詞”:有數感、符號意識、空間觀念、幾何直觀、數據分析觀念、運算能力、推理能力、模型思想、應用意識和創新意識。這些核心詞是貫穿于整個初中數學教學過程,老師的目標也就是維繞著這些核心詞來開展自己的教育教學工作。
二、二元一次方程組與學生的核心素養
首先,方程在人教版教材的七至九年級的數學教材中,這一知識點在學生學習過程中先后出現3次:七年級上冊第二章(一元一次方程),七年級下冊第八章(二元一次方程組),九年級上冊第二十二章(一元二次方程)。顯然,二元一次方程組這一章是對前面學習過的一元一次方程有關知識的繼承和檢查鞏固,又為以后的一元二次方程的學習打下堅實的基礎。二元一次方程組的知識不僅是學生加深對方程知識的理解,也是一次函數學習的起點,甚至是線性方程入門的基礎知識。二元一次方程組的這種“歷史”地位,使得它在培養學生的數學素養方面有著舉足輕重的作用,承前啟下,溝通了許多學生學習的節點。學生的數感(數量感悟)、符號意識(設未知數)、數據分析觀念(審題)、運算能力(解方程)、推理能力(數量關系)、模型思想(列方程)、應用意識(應用方程組)和創新意識在這一章節中可以得到充分培養和展示。
三、二元一次方程概念的教學設計
在教學中,如何設計才能達到或者說才能有意識地去培養學生的核心素養。下面以二元一次方程組概念課教學設計來展示這一教學理念。
教學設計:
(一)課程引入(創設情境)
1.小莉買花送給媽媽,一共花24元,玫瑰每支2元,買了9支,康乃馨每支1元,問小莉買了幾支康乃馨?
解:設小莉買了x支康乃馨,可列方程:
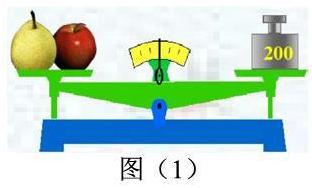
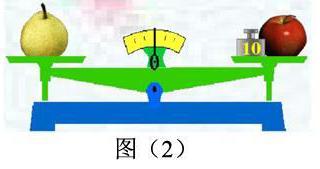
2.一個蘋果和一個梨的質量合計200克(如圖1),這個蘋果的質量加上一個10克的砝碼恰好與這個梨的質量相等(如圖2),問蘋果和梨的質量各為多少克?
問題1從學生的最近知識區域出發,有意識的引導學生進入設未知數,列方程的思維當中來,也是讓培養了學生的數感,當看到此類數據時,大概應用什么類型的工具來解決問題。這個問題1設計簡單明了,就是要為后面的二元一次方程組講解,留有足夠的時間。此種類型的問題不宜過多,以免花太多時間去復習舊有知識。同時也需要對所列的一元一次方程進行概念上的重溫,為二元一次方程組的講解做好充分的鋪墊。
問題2使用了與問題1相近的內容,并加上天平的圖示,充分讓學生領悟方程(等式)的固有屬性,其蘊含的等量關系將替移默化到學生的腦海中。簡單清晰的內容,大大減少學生在閱讀時產生的障礙,有利于老師引導學生去思考新的問題得出新的結論。這兩個問題的設計是互相應證,互相作用于學生的學習和思考過程。問題2之所以沒有設未知數,就是為了讓學生在這種條件下能否喚醒自己舊有知識的儲備,是否能形成符號感,能去自覺而又不自覺(主動思考)地合理分析問題,并有意識地運用方程模型來解決遇到的問題。雖然,或許求不出二元一次方程組的解,但已經是邁出了最為有力的一步,其行為已經屬于一種創新。對于老師而言,早就知道是列方程組,但對于學生來講,這是第一次運用一元一次方程來解決一個遇到的新問題,其創新性不言而喻。學生也正是在這種情境下,感悟到自己的能力和學習的愿望,從而推動了整個課堂的學習進程。當老師引導學生設出兩個未知數的方程時,下面的課程內容也就順理成章了。
(二)新課學習(師生互動,探索新知)
1.二元一次方程
觀察所列的方程:x+y=200
x=10+y
提出問題:
(1) 這兩個方程與問題1的方程相同嗎?
(2)與問題1對比,相同點和不同點,是什么?
(3)給這兩個方程起個名字,給出這種類型的方程定義。
(老師整理歸納、進行板書)
2.二元一次方程的解(學生討論完成)
(1)已知二元一次方程x+y=200,填寫下表:
(2)已知二元一次方程x=10+y,填寫下表:
二元一次方程的解在這里呈現,為引導學生去思考二元一次方程組的解埋下伏筆,并順利地得出二元一次方程組。
3.二元一次方程組(學生討論、老師引導)
由單個二元一次方程的解的無限性,從而想到要解決問題2的問題,顯然需要對于所列出的兩個方程進行同時的思考才能解決,由老師(或學生)來引導學生把兩個方程聯系起來,得出二元一次方程組。舊知識產生新知識,讓學生經歷從無到有,體驗學習的趣味性,推理性。二元一次方程組概念的獲得過程,應當充滿了邏輯性,充滿了數學研究過程的藝術之美。如果老師把種思考的過程一筆帶過,那么這節課的美妙之處,點睛之筆就無從說起了,學生也就只是感受到數學的冰冷和枯燥無味。
4.請判斷下列各方程組中哪些是二元一次方程組,哪些不是,并說明理由。
通過這個小練習的辨析,加強學生對概念的理解,去偽存真,讓學生把握準概念的外延。
5.二元一次方程的解
以表格的形式來展示:
(1)已知二元一次方程x+y=200,填寫下表:
(2)已知二元一次方程x=10+y,填寫下表:
學生通過表格,更清楚地去理解二元一次方程組的解的意義,從而抓住解的內涵,與二元一次方程的解互相作用,形成新的知識點和知識結構。
6.練習
判斷以下說話是否正確:
(1)方程2x+y=5的解是

