機會網絡自私節點的Bertrand博弈與激勵機制研究

吳 青，曾 鋒

中南大學 計算機學院，長沙 410000

1 引言

隨著手機終端和無線技術的發展，機會網絡[1]日益成為了大家關注的熱點。機會網絡是由無線自組織網絡和延遲容忍網絡[2]演化而來的新型網絡。在傳統的無線網絡中，消息傳送的源節點和目的節點之間至少需要有一條完整的通信鏈路存在。然而，在真實的網絡環境中，由于隨時可能發生網絡中斷，不能保證源節點和目的節點之間存在持久的通信鏈路。機會網絡與傳統網絡不同的是機會網絡中源節點和目的節點之間不需要一條完整的通信鏈路，節點之間轉發消息通常是基于節點移動產生的機會性的接觸。機會網絡采用一種“存儲-攜帶-轉發”的路由方式來進行數據交換。也就是說，如果節點沒有找到合適的中繼節點，消息將會存儲在節點的內存中，節點會攜帶著消息移動，直到遇到合適的中繼節點，消息才會被轉發。

機會網絡中數據傳輸成功主要基于節點之間的協作，因此，數據傳輸的前提是路由中的中間節點都愿意轉發數據包。但是在許多應用中，作為機會網絡節點的移動設備，由人攜帶，其處理能力、存儲空間、電池電量和等資源都是有限制的，節點很可能傾向于選擇自私行為。它們可能只想接收感興趣的消息，拒絕接收對它們沒有用但對其他節點有益的消息。如果節點都是理性的，節點將會顯示出自私性，為節省自己的資源而不會為其他節點轉發消息。文獻[3]的研究工作表明節點的自私行為嚴重損害了機會網絡中數據傳輸的性能。但是，節點是理性的，只要有利可圖即可參與合作轉發消息，因此可通過相關利益激勵節點從而提高網絡的整體性能。

目前，機會網絡中的激勵機制主要分三類，分別是針鋒相對（TFT）激勵機制[4]、聲譽激勵機制[5-6]和虛擬貨幣激勵機制[7]。TFT機制的主要思想是利用博弈論根據互惠原則構建模型，節點轉發給其他節點的數據量與從其他節點接收到的數據量相同。在實際網絡環境中，由于業務不對稱，很難在TFT 激勵機制中實現良好的性能。在聲譽激勵機制中，系統記錄每個節點的歷史協作行為，并且給每個節點提供聲譽值以評估它是否是自私的。此外，聲譽值動態變化，參與消息轉發的節點會獲得聲譽值的增加，聲譽激勵機制會選擇具有較高聲譽值的節點來轉發消息。然而，聲譽機制無法區分高信任度節點，導致對節點的激勵能力不足。在貨幣激勵機制中，源節點必須向轉發消息的中間節點支付虛擬貨幣，需要第三方管理，并且節點沒有差別定價方案。

如上所述，這三種類型的激勵機制在激勵節點參與消息轉發方面均存在不足之處。本文運用博弈論和虛擬貨幣分析節點之間的交互，提出一種基于Bertrand博弈的激勵機制。通過定義博弈參與者的效用函數，找到各方最佳策略，分析定價策略找到唯一的納什均衡，這個納什均衡點會讓每個節點都獲得最大效用。與已有研究工作不同，本文對參與節點實行兩階段的激勵。由于節點中的消息傳輸包括兩個階段，即從其他節點接收消息的階段和把消息轉發給其他節點的階段，因此應鼓勵每個節點不僅要從源節點接收消息，還要將消息轉發給其他節點。本文的工作提升了節點參與消息轉發的積極性，提高了數據傳輸的性能，且避免了只接收消息不轉發消息的丟包行為。

2 相關工作

許多學者對機會路由進行了廣泛的研究，提出了各種類型的消息轉發方法和路由算法，目的是提高數據傳輸速率，同時降低網絡開銷。

經典的Epidemic[8]路由算法泛洪的向身邊的每一個節點傳遞消息，也就是說源節點只要遇到下一跳節點就會把消息傳出去，不考慮網絡開銷。理論上，Epidemic路由算法有很高的傳遞率，但是帶來的網絡開銷也很高。經典的Direct[9]路由要求源節點把數據存儲到內存，遇到目的節點后才傳遞給目的節點，也就是說遇到任何下一跳節點都不轉發，直到遇到目的節點，才把消息轉發給目的節點。Direct路由算法雖然有很低的網絡開銷，但是傳遞率也很低。基于Epidemic和Direct路由算法，出現了許多有效的路由算法[10-12]，這些算法在消息傳遞成功率和網絡開銷之間進行權衡，在某些情況下具有良好的性能。然而這些傳統的路由算法都基于一個完美的假設，即網絡中所有的節點都會主動轉發消息給其他節點，不會拒絕轉發消息。但在真實的網絡環境中，作為機會網絡節點的移動設備由人攜帶，由于存儲空間、電池電量和其他資源的約束，節點往往是自私的。在Epidemic 路由中，如果所有節點都是自私的，則Epidemic路由方案會變成Direct路由。

機會網絡中節點自私問題最近引起了許多研究者的關注。在文獻[13]中，探索了節點合作對經典路由算法的影響，如Epidemic、Two-Hop，Binary Spray and Wait[14]等，提出了一種簡單的激勵機制，定義了協作度來提高三種路由算法的有效性，發現節點之間的協作度可以影響網絡的傳輸率。在文獻[15]中，提出了一種使用公平定價機制來激勵節點的拍賣激勵機制，將定價過程建模為拍賣博弈。該博弈能夠實現貝葉斯納什均衡，其中每個中間節點的利潤可以最大化。在文獻[16]中，提出一種基于博弈論的多功能激勵機制，叫Multicent，該機制不僅激勵節點參與消息傳遞，而且鼓勵節點遵循既定的規則實現期望的行為目標。在文獻[17]中，從博弈論的角度提出了一種激勵機制，它將個體自私和社會自私結合起來，提高機會網絡的性能。這個機制將兩個節點之間的消息傳輸映射為Rubnistein-Stahl 三次討價還價博弈，利用虛擬貨幣構建合適的價格函數，考慮節點資源和節點之間的社會關系進行數據傳輸。該機制主要的缺點是帶來數據傳輸能耗高，延遲大。在文獻[18]中，提出了基于Stackelberge 博弈模型機制（SEIR），給予中繼節點最好的獎勵以消除中繼節點的自私行為。為了避免節點的虛擬報價，提出了一種討價還價博弈，但這會導致一些資源的損失，從而導致高延遲和高消耗。在文獻[19]中，提出了一種基于博弈的激勵策略（GIS），該策略利用基于二人交易的三次議價模型，允許源節點根據博弈得出的最優價格直接支付中間節點，不需要第三方。在文獻[20]中，基于雙方拍賣提出一種叫CANCMDA 的機制。該機制解決網絡阻塞和節點自私的問題，雙方拍賣交易過程是一個貝葉斯均衡。但是，該機制只適用于單拷貝路由。在文獻[21]中，提出了一種叫NISOVCM 機制，設計了一種透支虛擬貨幣機制，以節點消息轉發能力作為擔保，解決虛擬貨幣不足和虛假報價問題。當消息交易無法完成一次完成時，交易雙方將根據資源狀態和財富狀況進行第二次討價還價來抑制雙方之間的虛假報價。但是，該機制不能有效改善網絡的消息傳輸成功率。在文獻[22]中，基于聲譽機制建立了動態模型，為社交網絡服務中的信息共享明確了激勵機制。在文獻[23]中，設置了一個獎勵機制，這個獎勵是設置預期交付成本的最小數量，獎勵僅給予作為第一個將消息傳遞到目的地的中繼節點。

上述激勵機制一定程度激勵了節點參與消息傳遞。然而，對一個節點來說，消息傳輸有兩個階段，首先從發送節點（源節點）處接收消息，然后攜帶著消息在移動中機會性地將消息轉發給其他節點。如果某些節點只接收消息，而拒絕轉發消息，則可能導致消息丟失。由于上述機制都是一階段的消息傳遞激勵，節點不能最大限度被激勵，兩階段激勵機制將更好地激勵節點參與消息傳遞，提高傳遞成功率。在已有工作的基礎上，本文設計了一種激勵機制，運用博弈論分析節點合作行為，找到節點參與消息傳遞的最佳策略，對節點進行兩階段激勵，鼓勵每個節點不僅從源節點接收消息，且將消息轉發給其他節點。

3 系統模型

本文提出了一種基于Bertrand 博弈的激勵機制（Bertrand Game-based Incentive mechanism，BGI），激勵自私節點參與機會網絡中的消息傳遞。BGI 包括節點之間交互的定義，以及參與消息傳遞節點的獎勵機制和定價機制。本文把消息傳輸的過程類比為市場中貨物的交易，假設攜帶消息的節點是買方，中繼節點是賣方，賣方為買方轉發消息獲得收益，源節點需要從中繼節點處購買服務用于消息傳送。

3.1 交易模型

在機會網絡中，假設節點的數量是n，節點集合是N={1,2,…,n}。節點可以攜帶多個消息，節點不僅可以是消息的源節點，而且可以是另一個消息的目的節點，它還可以在消息傳輸中充當中繼節點。但是，在同一時間，節點只能轉發一條消息給其他的節點。在圖1所示的模型中，消息發送方稱為源節點，準備接收和轉發消息的節點稱為中繼節點。另外，模型中會有一個兌換點，機會網絡中固定的基站、服務器，以及移動中的管理節點均可擔當模型中的兌換點。源節點發送消息之后，可以去兌換點獲取應得的虛擬貨幣。

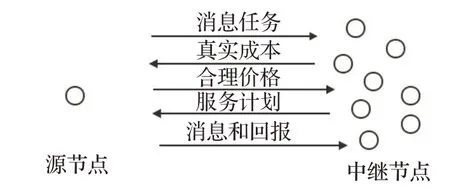
圖1 源節點和中繼節點的交易過程

在本文的模型中，源節點和中繼節點之間的交互有這幾個步驟：第一步，源節點把轉發請求廣播給周圍節點，源節點附近的節點都是候選中繼節點，候選節點接收到源節點的請求后會考慮是否為源節點轉發消息。第二步，對于準備為源節點轉發消息的節點，它們以轉發消息的成本回應源節點，并且不同的節點可能具有不同的成本。第三步，源節點把轉發消息的價格回復給候選節點，不同候選節點收到的價格可能是不同的，但源節點需要制定一個合適的價格吸引中繼節點轉發更多的消息。第四步，根據源節點給定的價格，每個中繼節點會制定轉發計劃，決定為源節點轉發多少條消息，這個計劃不僅影響中繼節點的效用，也會影響源節點的效用。最后，源節點把消息傳送給中繼節點，并以虛擬貨幣形式給予中繼節點報酬。

在消息傳輸中，參與者應該從源節點處接收消息，然后將消息轉發給其他節點。為了最大限度地鼓勵節點，本文對每個節點提供兩階段激勵，也就是說，節點可以分別從接收和轉發消息中分別獲得獎勵。源節點可以從兌換點處獲得轉發的每條消息c的虛擬貨幣的獎勵。中繼節點接收消息的獎勵來自源節點。一旦中繼節點接收到消息，它將成為下一輪消息傳輸中的源節點，它要找到其他節點并把消息轉發出去，重復此過程，直到最終目的節點收到消息。

本文將源節點和中繼節點之間的交互建模為商品交易過程，并基于博弈論分析交互雙方的最佳策略，即源節點給出最佳價格，中繼節點確定最佳轉發數量，這個機制激勵更多節點參與消息傳輸并實現自身利益最大化。對于在博弈中充當買方的源節點，它們期望給中繼節點轉發消息的價格盡可能低，這樣源節點可少付出。然而，作為服務銷售商，中繼節點期望更高的價格并轉發更多的消息，因為它們可以獲得更多的獎勵。因此，對于轉發消息定價，較高的價格將導致對源節點的獎勵較少，但對中繼節點的獎勵較多，雙方之間存在利益的博弈，下面本文將討論如何定價會讓雙方都滿意。

3.2 效用函數

從源節點和中繼節點的交易模型可知，如果源節點給的價格大于中繼節點傳遞消息的成本，中繼節點將會執行它的服務計劃。對源節點來說，它必須考慮中繼節點的成本以及它們可以轉發的消息數量，并確定一個合適的價格，這個合適的價格可以吸引節點傳遞更多的消息，同時自己的效用也最大。中繼節點效用受它們決定接收的消息數量的影響。但是，節點接收的消息越多，成本就越高。因此，中繼節點的效用將在一定程度上飽和。

假設中繼節點j從源節點i接收到ai個消息。中繼節點j的效用函數定義為等式（1），并將源節點i的效用函數定義為等式（2）：

式中，Uj代表中繼節點j的效用，pj代表中繼節點j從源節點i處收到一條消息的價格，cj代表中繼節點轉發一條消息的成本，b是飽和系數。

源節點i的效用是將消息轉發給中繼節點j的獎勵，并且轉發的消息越多，效用就越大。因此，源節點的效用跟轉發消息的數量是成正比，在等式（2）中，c是系統參數，需要滿足c>pj，這意味著任何源節點轉發一條消息的價格是一樣的。

3.3 成本的真實性證明

在源節點和中繼節點之間的交互中，中繼節點需要向源節點發送轉發消息的成本。從長遠來看，中繼節點會反饋轉發消息的實際成本給源節點。如果中繼節點j所給的成本是虛假的，則中繼節點的效用并不是最大的，這在數學上可以證明。假設中繼節點給源節點的是一個虛假的成本，源節點回報的價格是，根據等式（1），中繼節點的虛假效用用等式（3）來表示：

對于節點j轉發消息的真實成本cj，真實價格和效用分別是pj和Uj，比較Uj和，可以得到等式（4）：

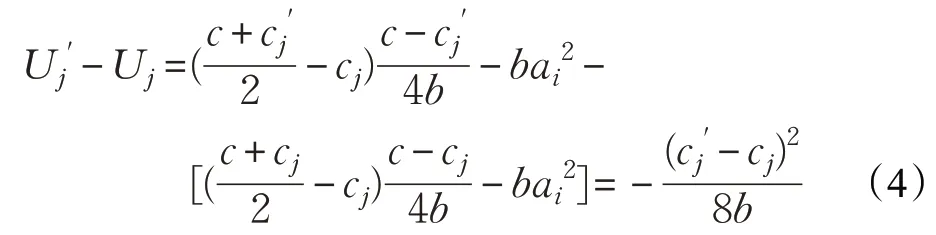
3.4 二階段激勵機制

一個節點成功傳輸消息需要兩個階段：第一個階段是該節點作為中繼節點從源節點處接收消息；第二個階段是該節點成為源節點把收到的消息轉發給其他節點。從BGI 節點交易模型以及節點的效用函數中可以看出，中繼節點只要接收源節點發送的消息，中繼節點j會從源節點收獲到每一消息pj的虛擬貨幣獎勵。為最大化收益，中繼節點考慮發送成本將選擇一個合適的接收消息數量，接收到消息后會獲得一定的虛擬貨幣，所得的效用可從等式（1）得出。這從接收消息階段激勵了節點在資源允許的前提下，盡可能多接收消息，以實現利益最大化。

中繼節點j收到消息后將成為所收到消息的源節點，在下一輪消息傳輸中，節點j選擇合適的中繼節點把消息轉發出去，節點j因為成功把消息轉發給下一跳節點可以從兌換點處獲得每一消息c的虛擬貨幣作為獎勵。源節點的效用跟所轉發的消息數量成正比，效用可從等式（2）得到。源節點想要獲得更大的收益就會傳遞更多的消息出去，這就從轉發消息這一方面鼓勵了節點傳遞消息。

節點可以分別從接收和轉發消息兩個階段中分別獲得獎勵。由于節點是理性的，節點會理性的選擇參與BGI二階段激勵機制。節點是理性的，節點在接收到消息后，由于轉發消息有利可圖，因此自私節點一定會把接收到的消息轉發出去以最大化收益。可見，二階段激勵機制可以避免節點收到消息后為節點資源后又把消息丟棄的行為，可以降低丟包率。

4 基于博弈論的定價分析

在本文模型中，為了最大化效用，源節點需要最佳定價策略，與之相應的中繼節點需要最佳的服務計劃。本文基于Bertrand[24]博弈建模分析源節點與中繼節點之間的交互。

在Bertrand 博弈中，源節點是買方，需要購買中繼節點的轉發服務。中繼節點是賣方，提供轉發服務給源節點，轉發消息是商品。如果商品的需求量給定，源節點可以基于中繼節點的成本計算出最合適的價格，這個價格會讓源節點得到的利潤最大。如果源節點給的價格比中繼節點的成本低，則中繼節點將不會參與源節點的消息傳遞。對于中繼節點來說，源節點的價格給定后，他們會決定為源節點轉發多少消息數量來最大化自己的收益。下文將分析雙方的最佳策略，并得到博弈中的納什均衡[25]。

納什均衡是每個參與者的策略對其他參與者策略的最優反應，即雙方在對方給定的策略下不愿意調整自己的策略。納什均衡是一種策略組合，因此每個參與者的策略同時是對其他參與者策略的最佳回應。本文將證明每位參與者的最佳回應是獨一無二的。在源節點的策略價格基礎上，中繼節點會制定消息傳送計劃（即它們愿意為源節點傳送的消息數量）以獲得最大效用。本文可以通過效用函數獲取到中繼節點的消息傳送計劃。

基于源節點的價格策略，中繼節點將制定策略，該策略是最大化效用的服務計劃。中繼節點j的效用函數是等式（1），可以得到Uj的第一階導數式（5）：

Uj的二階導數為式（6）：

由于b>0，Uj的二階導數是負數，因此Uj是一個嚴格的凸函數。因此令Uj的一階導數等于0，可以得到Uj的最大點ai，見式（7）：

如上式所示，中繼節點在價格和成本給定的情況下，最合適的轉發數量是，這個值可以最大化中繼節點的效用。

把等式式（7）代入式（2）中，可以得到源節點的效用，如式（8）所示：

對Pi進行一階求導，如式（9）所示：

Pi的二階導數用式（10）表示：

由于b>0，Pi的二階導數是負數，因此，Pi是一個嚴格的凸函數，Pi有一個最大值，令一階導數等于0，可以得到最佳的價格pj，這個值可以最大化源節點i的效用。

從以上的分析可知，源節點i和中繼節點j之間的博弈將會達到一個納什均衡點，意味著源節點i最好的策略是給中繼節點j的價格，中繼節點j最好的策略是為源節點i傳遞的消息數量。

5 模擬仿真

為了驗證BGI 激勵機制的有效性，本文在ONE[26]模擬器中進行了模擬實驗。在模擬實驗中，使用了Infocom5、Infocom6、Cambridge和Intel這四個真實數據集進行了實驗模擬，數據集的具體信息如表格1 所示。在模擬仿真中，每一個節點都以一個0.5～1.5 m/s的速度移動。每3 000～4 000 s就會有一個產生500 KB大小的消息，以及4 500 m×3 400 m 的地形尺寸。系統參數c和飽和系數b分別是10、1/2。

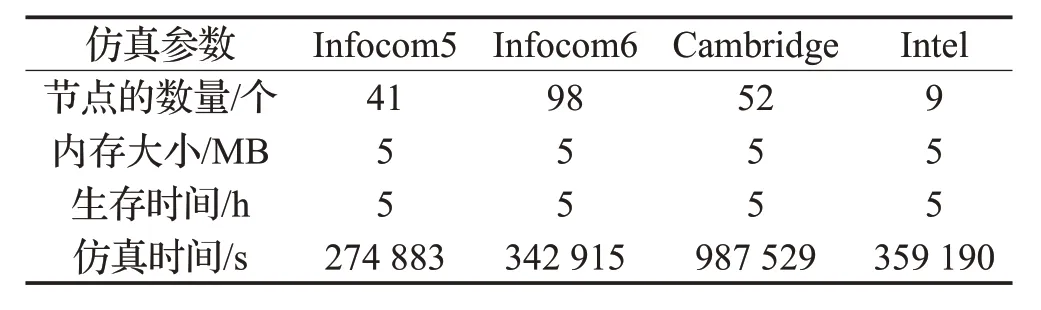
表1 四個數據集的仿真參數

5.1 性能指標

本文實驗選擇消息傳遞率，開銷率和平均延遲這三個因素來驗證激勵機制的效果。

傳遞率是消息成功到達目的節點的總數與實際創建的消息數量之比。

開銷率是指網絡中全部中繼的消息數（relayed_number）減去成功轉發消息數（delivered_number），然后再與成功轉發到目的節點的消息數之比。在數學上，可以定義為：

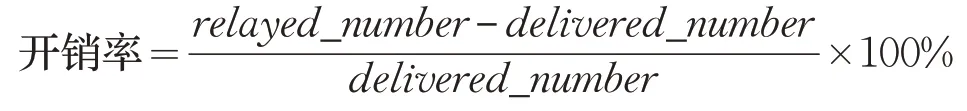
平均延遲是從消息產生到成功交付所花時間的平均值。

5.2 仿真場景

總所周知，存在的路由算法都是基于節點之間合作的。本文運行Epidemic路由算法，通過調整自私節點的數量來評估提出的激勵機制的性能。考慮下面這幾種場景：

（1）Epidemic+沒有自私節點(E+N)。在Epidemic路由的背景下，沒有任何自私節點，每個節點都會自發的轉發消息。

（2）Epidemic+自私節點 (E+S)。在Epidemic 路由的背景下，加上自私節點。自私節點會拒絕接收其他節點傳遞過來的消息，不參與消息傳遞。通過調整自私節點的數量，觀察實驗結果。

（3）Epidemic+自私節點 +BGI(E+S+BGI) 。在Epidemic 的背景下，加入自私節點，再加上BGI 激勵機制，調整自私節點的數量，觀察實驗結果。理論上，節點會被BGI激勵機制激勵，從而參加消息傳遞。

（4）Epidemic+自私節點+Reputation(E+S+R)。在Epidemic的基礎上，添加自私節點，再加上Reputation激勵機制，觀察實驗結果。

5.3 實驗分析

如圖2～5 所示，E+S中，沒有加入激勵機制，隨著自私節點數量的增多，交付率急劇下降。當自私節點比率為0 時，相當于每一個節點都是正常節點，網絡中沒有自私節點，就是經典的Epidemic路由協議。當自私節點不斷的增多，自私節點比率為1 的情況下，沒有中繼節點愿意傳遞消息，僅僅只有源節點不斷移動碰到該消息的目的節點，才把消息傳遞給目的節點，也就成了經典的Direct路由協議。

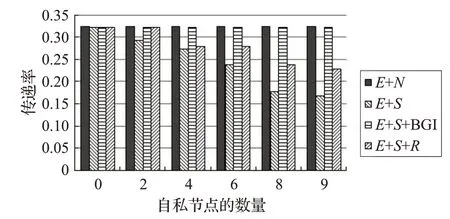
圖2 Intel數據集中傳遞率隨著自私節點數量的變化

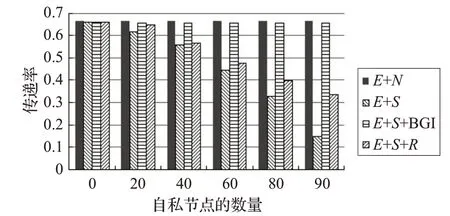
圖3 Infocom6數據集中傳遞率隨自私節點數量的變化

圖4 Infocom5數據集中傳遞率隨自私節點數量的變化

圖5 Cambridge數據集中傳遞率隨自私節點數量的變化

仿真結果顯示自私節點嚴重影響傳遞效率，如果加入BGI 機制，節點是理性的，它會為了自身的利益，考慮跟其他節點合作，傳遞率會逐漸上升。由于E+N中沒有考慮自私節點，因此E+N的性能僅呈現為零自私節點的情況。從圖2～5可以看出，當網絡中存在自私節點時，BGI 機制具有較高的傳遞速率，并且具有與E+N幾乎相同的傳遞速率，這表明了BGI激勵機制的有效性。與E+S+R相比，BGI 機制的平均交付率提高了31.4%。

隨著自私節點數量的增加，與開銷相關的仿真結果如圖6～9 所示。由于自私節點不參與消息轉發，因此E+S中的開銷會隨著自私節點數量的增加而減少。但是，在E+S+R和E+S+BGI 中，自私節點會被激勵參與消息轉發，因此E+S+R和E+S+BGI 中的開銷會跟隨著自私節點的數量的增加而增加，E+S+BGI的消耗比E+N稍低。

圖6 Intel數據集中開銷率隨自私節點數量的變化

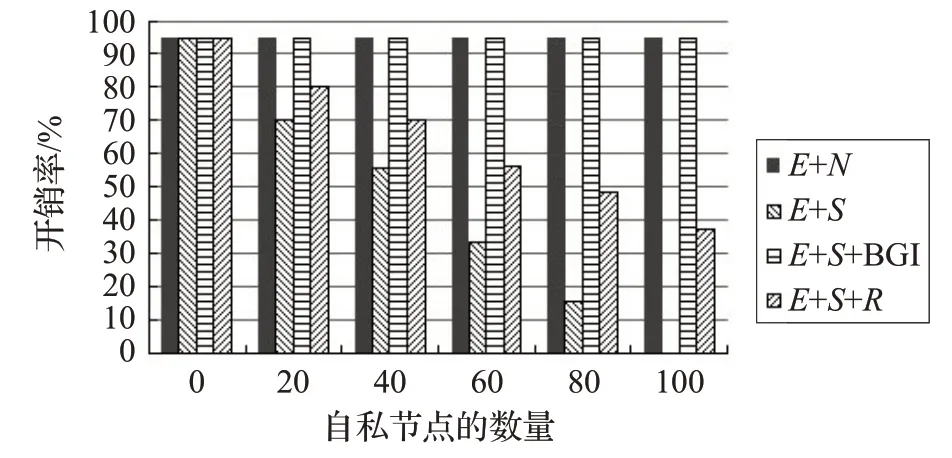
圖7 Infocom6數據集中開銷率隨自私節點數量的變化

圖8 Infocom5數據集中開銷率隨自私節點數量的變化

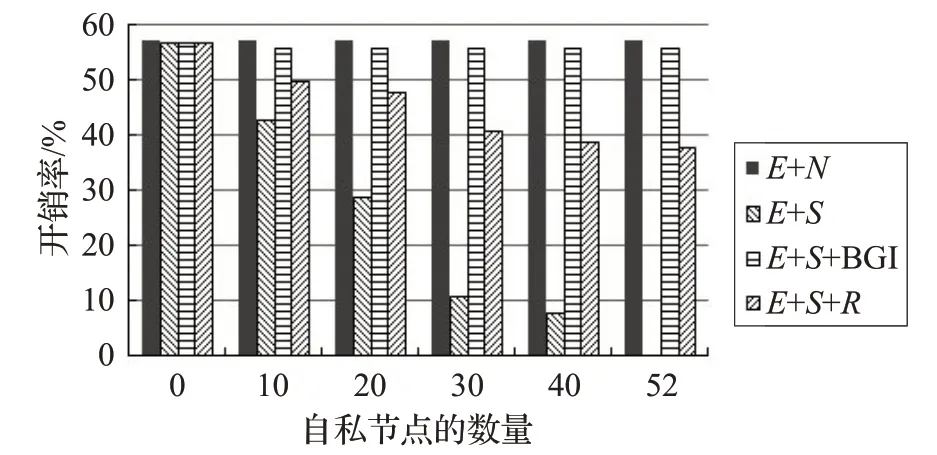
圖9 Cambridge數據集中開銷率隨自私節點數量的變化

隨著自私節點數量的增加，與平均延遲相關的仿真結果如圖10～13 所示。從仿真結果可以看出，因為BGI機制能夠激勵更多的自私節點去為其他節點轉發消息，相對于E+S和E+S+R來說，BGI有更低的延遲。跟E+S和E+S+R比較，BGI分別平均低11.8%和9.7%。BGI具有與E+N幾乎相同的平均延遲，E+N是沒有任何自私節點的情況。

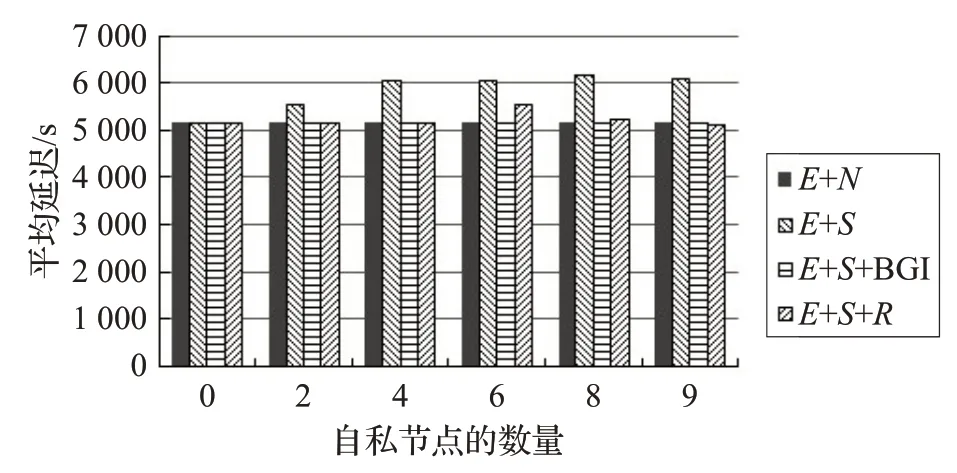
圖10 Intel數據集中平均延遲隨自私節點數量的變化

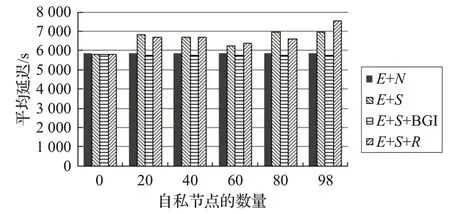
圖11 Infocom6數據集中平均延遲隨自私節點數量的變化

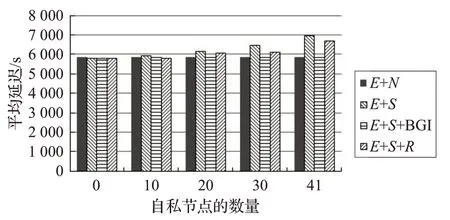
圖12 Infocom5數據集中平均延遲隨自私節點數量的變化

圖13 Cambridge數據集中平均延遲隨自私節點數量的變化

從消息傳遞率可以看出，BGI激勵所有節點參與傳遞，但是傳遞率并沒有與E+N一樣高，這是因為中繼節點會選擇合適的消息數量最大化自己的利益，這個合適的數量可能小于源節點本身的消息數量，這樣會有少量消息不會從源節點處傳遞出去。可以從等式（7）中看出，合適的消息數量與飽和系數b有關，通過調節飽和系數得到不同的情況。下面，本文分析在Infocom5數據集中飽和系數b對BGI機制的影響，Infocom6以及其他數據集中有類似的表現，限于篇幅，本文僅以Infocom5數據集來展示參數b的影響。

從圖14中可看出，飽和系數越小，傳遞率越高。從等式（7）中可以看出，合適數量與飽和系數b成反比。b越小，中繼節點的合適數量越大，源節點可以把更多的消息傳遞給中繼節點，E+S+BGI 的傳遞率則會增高。從圖15 可以看出飽和系數b對E+S+BGI 消耗率的影響，E+S+BGI 消耗率隨著飽和系數b的增加而減少。從圖16 中可以看出飽和系數對E+S+BGI平均延遲的影響，飽和系數越大，平均延遲越高。

圖14 Infocom5數據集中傳遞率隨飽和系數的變化

圖15 Infocom5數據集中開銷率隨飽和系數的變化

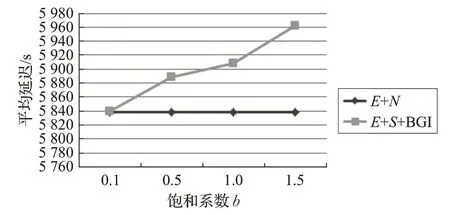
圖16 Infocom5數據集中平均延遲隨飽和系數的變化

6 結束語

本文定義了源節點和中繼節點之間的交易步驟以及效用函數，基于Bertrand博弈建模分析源節點與中繼節點的交互過程，源節點給定中繼節點傳遞消息的價格，基于該價格，中繼節點確定所傳遞的消息數量。在源節點和中繼節點的博弈中，存在一個唯一的納什均衡，使得雙方效用都是最好的。仿真結果表明，本文所提激勵機制可以促進自私節點之間的協作，提高路由算法在傳遞速率和延遲方面的性能。與基于聲譽的激勵機制相比，BGI機制能使消息傳遞成功率提高31.4%、平均時延降低9.7%。