一種基于預處理迭代算法的核磁共振T2譜反演?
李鵬飛 佟喜峰 游博洋
(東北石油大學計算機與信息技術學院 大慶 163318)
1 引言
在地球物理、遙感技術、工業控制以及信號(圖像)處理等眾多科學技術領域中,一般都存在反問題的求解問題。這些反問題對應的數學模型很多都是病態線性方程組。
在求解病態線性方程組時,其數值解是不穩定的。由于系數矩陣和右端常數項量大多來源于原始觀測資料,而原始資料中存在的觀測誤差會因系數矩陣的病態性被放大,導致算法的數值解偏離真解而失去意義。以Ax=b方程組為例說明病態系數矩陣對解的誤差的放大作用。在其系數矩陣和右端向量存在觀測誤差時,則變為如下形式:

式(1)有如下估計式成立[1]:


其系數矩陣的譜范數意義下的條件數為2503,屬于比較嚴重的病態程度。精確解為x1=-100,x2=-200。假設系數矩陣存在擾動,則方程組變為
則得到一個截然不同的解:x1=40000,x2=79800。
當病態系數矩陣的條件數很大時,在不對系數矩陣做出預先處理的情況下,就直接使用常規的求解方法得到的數值解誤差會非常大甚至無法獲得數值解。所以,目前對于病態線性方程組求解一般都圍繞先對病態系數矩陣進行改良這種方法開展工作,即先對病態系數矩陣進行預處理,將其改造成良態矩陣后,再進行求解。文獻[2]中SSOR-ICCG算法,其迭代過程不影響ICCG算法的收斂性,而且通過SSOR預處理來降低系數矩陣的條件數,從而提高算法的穩定性,加快收斂速度。該算法要求系數矩陣必須對稱正定。文獻[3~4]中均提到正則化方法求解病態的反問題,方法是對病態矩陣進行正則化改造,使之變為良態,然后用這個正則解作為待求方程的近似解。這類方法中如何確定正則化參數,使正則解更好地逼近原問題的解比較困難。根據原始觀測數據中誤差水平是否已知,有后驗策略和先驗策略兩種方式來確定正則參數。黃小為[5]認為譜截斷的正則化方法甚至比Tikhonov正則化方法更為有效,因此基于截斷奇異值分解法[6~10]被越來越多的科研工作者應用在各自領域的反問題求解過程中。此外,人工神經網絡和基于進化計算一類的智能優化算法[11~15]也被應用于病態的反問題求解。
本文將病態系數矩陣進行改造,在降低其病態性的同時,構造了一種簡單的預處理迭代算法,來求解嚴重病態的線性方程組。
2 預處理迭代算法設計
設有如下形式線性方程組:

其中,(aij)n×n>0 。,構建對角陣D,并將DX疊加在式(3)兩端,得式(4):

根據式(4)得:

要確保迭代公式(6)有效則必須滿足D+DA可逆,以及迭代矩陣(D+DA)-1(D-K)收斂兩個條件。由于矩陣D和DA均為元素大于零的對角陣,所以D+DA必可逆。下面對迭代矩陣的收斂性予以證明。
3 迭代矩陣收斂性證明
結論1:設式(3)中系數矩陣A為實正定方陣,則式(6)中迭代矩陣(D+DA)-1(D-K)必收斂。
證明:設λ為系數矩陣A的特征值,λ'為迭代矩陣(D+DA)-1(D-K)的特征值,則對于這兩個矩陣有如下等式成立:

對于系數矩陣和迭代矩陣的任意一個特征值λi,,有:

根據所構建的對角陣D可知,式(6)中迭代矩陣嚴格行對角元素占優,且主對角線元素均大于0,依據文獻[16]中定理3的結論:矩陣中任一特征值實部必大于0。則迭代矩陣為正定矩陣,所以>0。又因為A正定,所以λ>0。a>0,d>0iiii(已知),所以<1。由此得出:0<<1,因此迭代矩陣收斂。證畢。
4 預處理迭代算法對比實驗測試
4.1 Hilbert病態線性方程組測試
以20階Hilbert病態線性方程組為測試實例,其中:
Hilbert矩陣元素:

右端向量:

在實際測試過程中,為了驗證算法的穩定性,取一組xj=1(j=1,2,…,20)作為真解代入方程組,求得右端向量后,在其基礎上添加SNR=50的高斯白噪聲。表1中對比了本文中設計的預處理迭代法、Matlab中自帶的非負最小二乘法優化函數、遺傳算法和雅可比迭代法四種方法求解結果。預處理迭代算法的停止條件為當0.001退出迭代。遺傳算法采用了Matlab中自帶的遺傳算法工具箱,其除了具有簡單遺傳算法的選擇、交叉和變異算子之外,還有精英個體復制策略、遷移策略和懲罰函數等算子,用來提高數值解的精度。
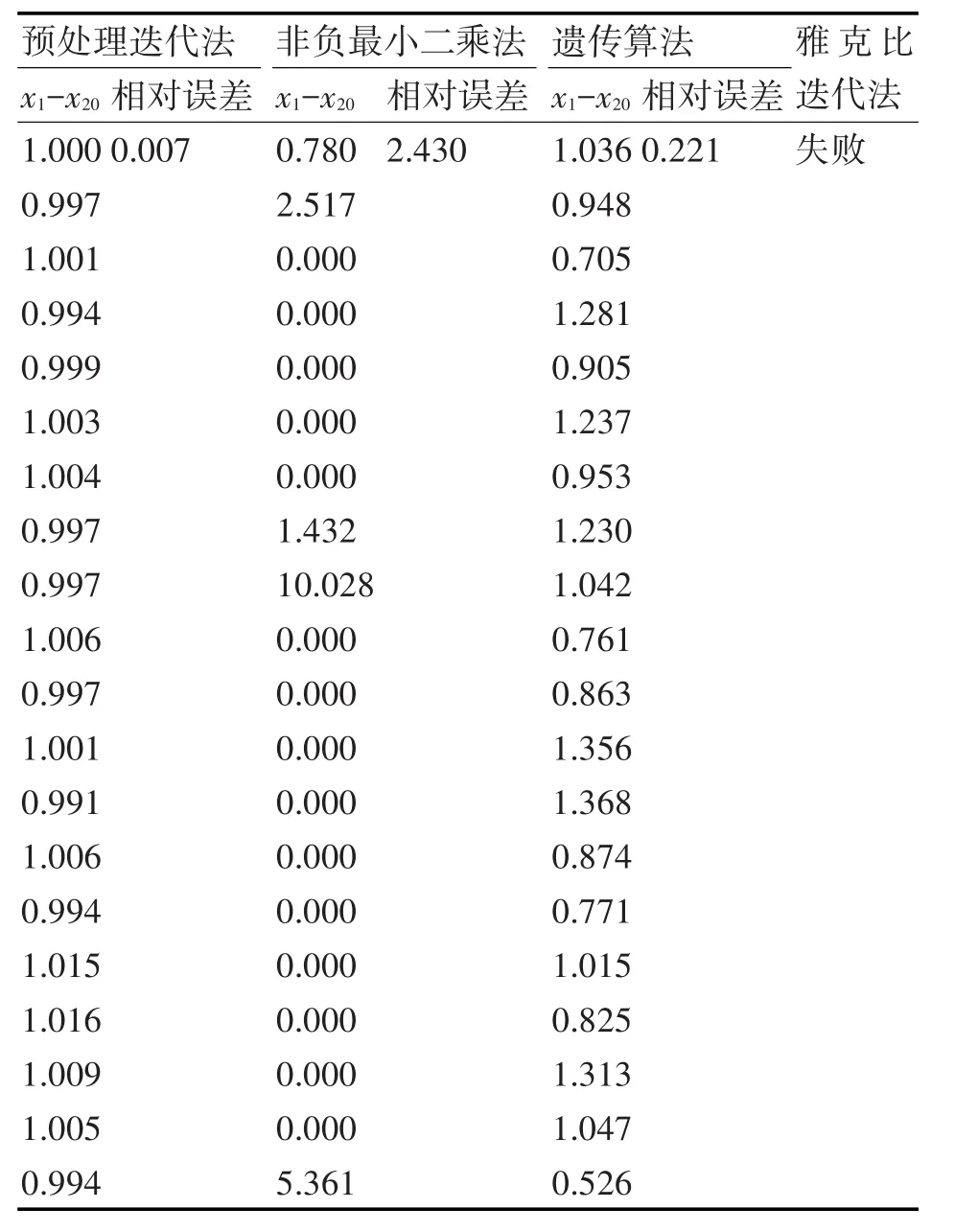
表1 20階Hilbert病態線性方程組求解對比
4.2 核磁共振T2譜模型反演測試
根據核磁共振測井理論可知,氫原子核系統磁化強度矢量的橫向分量是按指數規律衰減的,由CPMG脈沖序列測得的回波串也按指數規律衰減。儲層巖石通常存在一個孔隙尺寸分布,并且常常含有多種流體成分,此時孔隙中存在多種弛豫組份,即橫向弛豫時間常數(T2)不是單值,而是一個分布,稱之為T2譜[17]。由CPMG脈沖序列測量記錄的自旋回波串按多指數規律衰減,即各單指數衰減的疊加。回波幅度與橫向弛豫分量初始幅度之間滿足式(10)關系[17~18]:

式中:bi為CPMG脈沖序列測量記錄的第i個回波幅度;Ej為第j個橫向弛豫分量的初始幅度(正數);T2j為第j個橫向弛豫分量衰減的時間常數;TE為CPMG脈沖序列測量記錄的回波間隔;N為橫向弛豫分量的個數;M為回波個數。
T2譜反演就是根據預設的T2值和儀器測得的回波串數據,求解出Ej來擬合測得的回波串數據。這一過程稱為解譜或多指數擬合。其實質是求解M個方程,N個未知數的線性方程組。
在實驗室以實測的某井巖心回波數據為T2譜反演模型的右端向量,回波間隔表達式取TE=322.65+(i-1)×300,橫向弛豫分量的個數取N=128,回波個數取M=2048。某井巖心實驗參數表如表2所示。

表2 某井巖心實驗參數表
該井巖心數據構成的模型為超定線性方程組,將其左乘系數矩陣的轉置矩陣,則原方程組變為其正則方程組。使用預處理迭代算法對其進行反演解譜,并與實驗室中英國牛津核磁共振分析儀(MARAN)自帶的解譜軟件包的解譜結果進行了對比,如圖1所示。

圖1 預處理迭代法和MARAN解譜對比圖
5 結語
在20階Hilbert病態線性方程組的測試實例中,添加了SNR=50的高斯白噪聲。此時,系數矩陣數值是精確的,而右端向量相當于有了擾動δb。經過Matlab中計算,其系數矩陣譜范數意義下的條件數為1.53×1018,已經嚴重病態。觀察表1可以得出:預處理迭代法的相對誤差為0.007,精度還是相當高的。遺傳算法的某些解偏離精確解比較大,導致相對誤差也比較大。而非負最小二乘法的數值解除已經嚴重失真,失去了意義。對系數矩陣未經處理而直接用雅可比迭代法進行求解,算法失敗,這也印證了文中前面所提:如果不對病態矩陣進行預處理而直接使用常規的解法進行求解時通常會失敗。求從求解的速度來看,在雙核i3-2130,主頻3.4GHz,4GB內存的臺式機上,預處理迭代法和非負最小二乘法求解時間均為0.01s的數量級,而遺傳算法(進化代數2000代,停滯代數50)的求解速度最慢,約為10s數量級。
對于用實驗室巖心數據構建的T2譜反演模型,回波間隔和回波幅度均為儀器測定,所以反演模型中系數矩陣和右端向量分別存在擾動δA和δb。根據儀器測定的參數,按照式(10)計算,系數矩陣譜范數意義下的條件數為1.253×1019,病態性比測試實例1更重。將原方程組轉換為正則方程組后,系數矩陣病態性會進一步加劇(譜范數意義下的條件數為7.113×1020)。此時,對于任何算法,求出穩定的數值解難度都非常大。預處理迭代算法是在對病態的系數矩陣改造的基礎上而構成一個迭代公式,并對其進行求解,所以解的精度和穩定性得到了有效的提高。通過觀察圖1可以得知預處理迭代算法反演結果與牛津核磁共振分析儀自帶的解譜軟件的反演結果基本吻合,譜的形狀與變化趨勢基本一致。因此,與比較昂貴的進口儀器相比,采用預處理迭代算法進行反演,具有更好的性價比。
以上兩個測試實例具有較好的代表性,既有理論數據構造的系數矩陣,也有儀器實測的原始數據形成的具有擾動的系數矩陣和右端向量,能夠更好地檢驗算法的數值解穩定性。從解譜結果對比來看,可以得知預處理迭代算法是求解嚴重病態線性方程組的一種有效算法。

