采用分等級學習策略的二進制粒子群優化算法?

戴海容 李浩君 張鵬威

（1.浙江金融職業學院工商管理學院 杭州 310018）（2.浙江工業大學教育科學與技術學院 杭州 310023）

1 引言

Kennedy和Eberhart最先提出了基本的粒子群優化算法［1］，基本粒子群優化算法被廣泛應用于具有連續性質的問題；為了解決實際生活中眾多離散型問題，Kennedy和Eberhart于1997年提出二進制版本的粒子群優化算法［2］（Binary Particle Swarm Optimization，BPSO）。但是二進制粒子群優化算法在尋優后期同樣存在易陷入局部最優、多樣性丟失現象，導致收斂精度低的問題。相關學者從參數優化［3～4］、種群優化［5～6］、混合優化［7～8］、變異算子［9～10］、速度更新［11］和映射函數［12～13］等多個角度對粒子群優化算法進行了改進，以提高算法的收斂性能和多樣性能。上述方法在一定程度上提升了BPSO算法的精度和多樣性，但是并不能從本質上解決精度與多樣性的矛盾問題；其中多種群優化角度還存在粒子數量多、計算量大的問題。因此，二進制BPSO算法的收斂性能還有較大優化空間。

本文借鑒雞群算法中的等級制度，提出采用分等級學習策略的二進制粒子群算法（HLBPSO）。HLBPSO算法根據適應度值將粒子分為三個等級，對每個等級粒子采取針對性的學習策略，實現算法性能提升；受變異算子能夠增加種群多樣性［9］的啟發，進一步提出逃逸算子用于劣勢粒子逃出所處區域，使劣勢等級粒子有能力朝著最優解探索；最后根據當前粒子與最優等級粒子之間距離的差分向量實現慣性權重自適應更新，提升算法精度，增強解的多樣性。

2 基本二進制粒子群算法

2.1 基本的BPSO算法

BPSO算法中的粒子速度更新方式與基本PSO相同；在粒子位置更新方式上，BPSO算法中設計了一種映射函數，用于將粒子速度值映射為粒子位置變換為1的概率。式（1）為BPSO中粒子速度更新公式，式（2）為BPSO算法中用到的映射函數，式（3）為粒子位置更新公式。

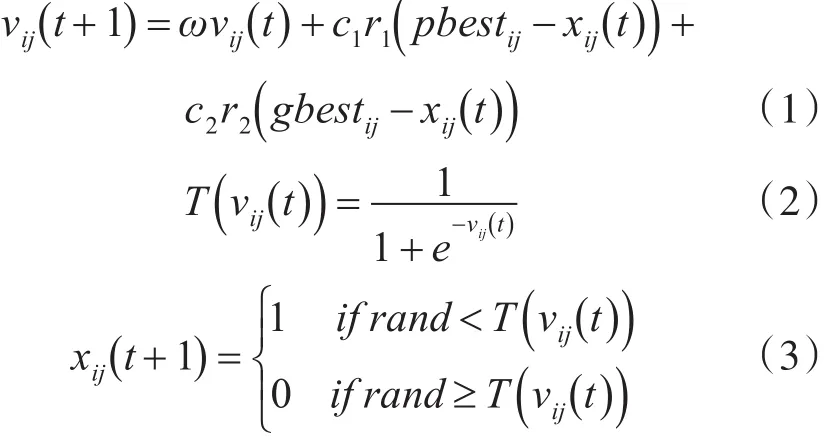
其中，vij(t +1)為粒子在t+1次迭代時的速度值，i表示的是當前粒子，j表示的是維度；ω為慣性權重；c1表示粒子向自身學習的比重，c2表示粒子向社會學習的比重；xij(t)表示粒子i的當前位置；T(vij(t))表示速度映射的概率值。

2.2 基本的雞群優化算法

雞群算法［14］（Chicken Swarm Optimization Algo?rithm，CSO）于2014年被提出，是通過對雞群尋找食物過程的模擬而設計的一種優化算法。目前，已出現對雞群算法眾多不同的優化策略，并成功應用到了問題求解當中［15～16］。雞群算法中每只雞作為求解問題的一個可能解，根據每只雞的適應度值將整個種群劃分為若干個子群，并分為公雞、母雞和小雞三類；其中每個子群中只存在一只公雞，而母雞和小雞有若干個，它們只在自身所處的群體中尋找食物，公雞是最靠近食物源的一類。在覓食過程中，通過向自身已有經驗和群體中公雞經驗不斷地學習實現自己的位置更新。在迭代過程中，每隔一定次數后重新按其目標函數值排序劃分其等級。

3 采用分等級學習策略的二進制粒子群優化算法（HLBPSO）

采用分等級學習策略的二進制粒子群優化算法（HLBPSO）借鑒雞群算法中的等級制度，根據適應度值把種群中適應度值較好的前2/10粒子設置為優勢等級粒子，適應度值較差的后3/10粒子設置為劣勢等級粒子，其他5/10為中間等級粒子。優勢等級粒子采取探索學習模式，旨在探索新的未知空間，尋求最佳解；中間等級粒子采取全局學習模式，向優勢等級最優粒子學習；劣勢粒子采取混合學習模式，向優勢等級最優粒子與中間等級最優粒子的差分向量進行學習，而且賦予粒子逃逸所處區域的能力。三種學習模式中的慣性權重根據當前粒子與優勢等級最優粒子間的距離實現動態更新。

3.1 分等級學習策略

在雞群算法中，公雞向更加廣闊的未知空間探索；母雞向所在子群公雞學習的同時，也向隨機挑選的公雞或母雞學習；小雞向所在子群的母雞學習。參考雞群算法中的學習機制，對其優化，最后確定HLBPSO算法的學習機制如下：

1）優勢等級粒子采用探索學習模式，探索學習模式下的優勢等級粒子受自身慣性驅使的同時，向更廣泛的未知空間學習，探索新解。公式如下：

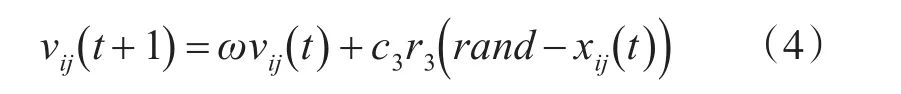
2）中間等級粒子采用全局學習模式；中間等級粒子向優勢等級最優粒子學習。gbestij表示優勢等級中的最優粒子，也是整個群體中的全局最優粒子。

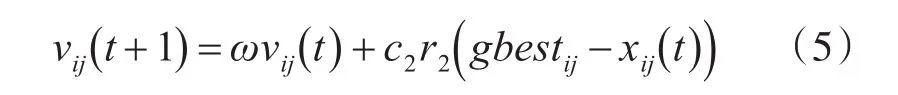
3）劣勢等級粒子采用混合學習模式。劣勢等級粒子向優勢等級最優粒子與中間等級最優粒子的差分向量進行學習；與此同時，由于劣勢粒子離全局最優粒子較遠，因此設計逃逸算子，使劣勢粒子以一定概率發生變異以達到提升算法尋優精度、增強種群多樣性的目的。式（6）中zbestij表示中間等級的最優粒子，ES表示逃逸算子。

3.2 逃逸算子設計

為了使算法避免陷入局部最優，增加解的多樣性，為劣勢等級粒子設計逃逸算子ES。劣勢等級粒子離全局最優解距離較遠，通過設置逃逸算子，在一定程度上讓劣勢粒子逃離自身所處區域，增加向全局最優解靠近的概率。逃逸算子如式（7）。

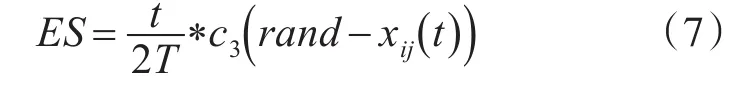
式中，t表示的是當前迭代次數，T表示最大迭代次數，rand表示的是（0，1）之間的隨機值，c3=0.01。

3.3 粒子位置更新

文獻［13］提出了弧形映射函數，并通過實驗表明了弧形比S型和V型具有更好性能。因此，HLB?PSO算法采用弧形映射函數將粒子的速度值映射為位置改變的概率，位置更新則使用非強制性位置更新程序。如式（8）、（9）所示：

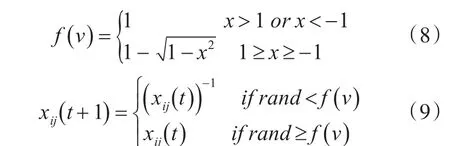
3.4 自適應慣性權重設計

慣性權重ω采用動態非線性策略進行更新，具體地，根據當前粒子與優勢等級中最優粒子間的歐式距離設計慣性權重調整策略。粒子間的歐式距離用表示，如式（10）所示；值較大時表明當前粒子i離全局最優粒子的距離較遠，需要將ω值增大，增強全局探索能力；相反，則減小ω值，提高局部開采能力；本文設計的慣性權重自適應更新方案如式（11）。

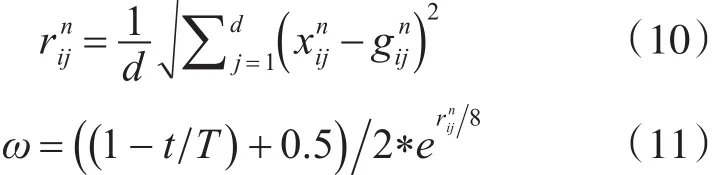
3.5 算法步驟

HLBPSO算法步驟如下：

1）對HLBPSO算法中的種群進行初始化；

2）如果迭代次數小于等于1，則采用式（1）實現粒子速度更新，并利用式（9）實現粒子位置更新，之后執行步驟7）；否則，執行步驟3）；

3）在迭代過程中根據粒子的適應度值將粒子種群劃分為不同的三個等級；

4）基于當前粒子與優勢等級最優粒子間的距離對慣性權重值進行自適應動態更新；

5）優勢等級粒子采用式（4）對粒子速度進行更新；中間等級粒子采用式（5）對粒子速度進行更新；劣勢粒子采用式（6）對粒子速度進行更新；

6）采用式（9）對粒子位置進行更新；

7）計算粒子適應度值；

8）判斷是否達到終止條件；如果達到，則執行步驟9）；如果否，則返回步驟3）；

9）輸出結果，算法結束。

4 仿真實驗分析

4.1 實驗設置

通過基準測試函數驗證算法的收斂性能是常用的驗證方法。本文通過將所提HLBPSO算法在6個測試函數上與三個對比算法進行對比來分析算法的收斂性能。測試函數選擇經典的Sphere函數（F1）、Step函數（F2）、Rosenbrock函數（F3）、Rastri?gin函數（F4）、Ackley函數（F5）、Griewangk函數（F6），其中，F1、F2、F3為單峰函數，F4、F5、F6為多峰函數。用到的6個基準測試函數如表1所示。

表1 基準測試函數

在對比算法選擇上，本文除了選擇基本的二進制粒子群優化算法BPSO［2］外，選擇最新提出的、效率較高的CBPSO算法［4］作對比；鑒于HLBPSO算法采用了文獻［13］中的弧形映射函數，所以也將文獻［13］中提出的ABPSO算法作為對比算法。各算法實驗參數設置如下：ω初始值為2，ωmax=0.9，ωmin=0.4；c1=c2=2；本文所提HLBPSO算法中c3=0.01；vmax=6。

實驗從收斂精度、成功率和收斂速度三個角度實現算法的對比。

收斂精度：由四個算法單獨運行30次獲得的平均值數據衡量；

成功率：算法收斂至指定精度的次數與運行總次數之比乘以百分比。在實際問題中，指定精度可以根據所求問題由多次實驗確定，或者由有經驗的專家確定。本文中指定精度由以下公式計算：

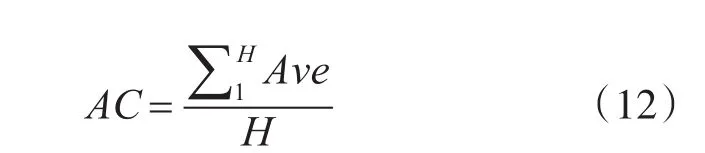
公式中AC表示指定精度，H表示算法個數，Ave表示各個算法得到的30次均值。

收斂速度：由四個算法的尋優過程衡量；

實驗環境為windows7操作系統，在Matlab中進行各個算法的編碼。硬件環境為intel酷睿處理器i5-4570，主頻為3.20GHz，內存為4GB。

4.2 實驗分析

由于智能優化算法在運行中存在著隨機性，為了減少這種現象對實驗結果的影響，將算法在6個測試函數上分別運行30次求取均值獲得實驗數據。如表2～表7所示，表2～表7展示了基本的BP?SO算法、最新提出的ABPSO、CBPSO算法和本文所提HLBPSO算法在不同維度、不同種群規模和不同迭代次數下的實驗數據。D表示維度，分別設置50維、150維、300維；N表示種群數量，分別設置30、40、50；T表示最大迭代次數，分別設置 100、300、500。通過不同維度、不同種群規模和不同迭代次數的實驗設置，充分驗證了HLBPSO算法的收斂性能和魯棒性。

表2 算法在函數F1上的實驗結果

表3 算法在函數F2上的實驗結果

表4 算法在函數F3上的實驗結果

表5 算法在函數F4上的實驗結果

表6 算法在函數F5上的實驗結果

4.2.1 收斂精度與成功率分析

從表2～表4中的實驗數據可以看出，在單峰函數F1、F2上，HLBPSO算法在不同維度、不同規模上具有最好的均值、方差和成功率，說明收斂性能優于對比算法；CBPSO算法雖然在成功率上與HLBPSO算法相同，但均值差于HLBPSO算法；AB?PSO算法在三個維度的均值和成功率上優于基本的BPSO，但在維度為150和300時，方差不如基本的BPSO；BPSO算法在三個維度上的收斂性能最差。在單峰函數F3上，CBPSO算法所獲均值最小，收斂精度最高，并在維度為50、150時找到了函數的極小值；HLBPSO算法在均值和成功率上優于ABPSO算法和BPSO算法；BPSO算法的性能最差。在三個單峰函數上，HLBPSO算法展現了較好的收斂性能。

從表5～表7中的數據可以看出，在多峰函數F4、F5、F6上，HLBPSO算法在三個維度上所獲的30次均值都是最小的，這表明尋優精度是最高的，而且成功率也高于對比算法，表現出了較好性能。特別是對于多峰函數F6，當維度在150、300時，HLBPSO算法找到了極小值。CBPSO算法在三個多峰函數上的表現僅次于HLBPSO算法，優于BP?SO和ABPSO算法；BPSO算法的尋優效果不如AB?PSO算法。在F4、F5和F6三個多峰函數上，HLBP?SO展現出了比對比算法更好的尋優性能，有著較高的收斂精度和成功率。

4.2.2 收斂速度分析

圖1～圖6是四個算法在函數為300維時的尋優過程，除了在測試函數F3上HLBPSO算法的收斂性能不如CBPSO算法，在其他五個函數上，HLB?PSO算法都展現出比其他算法更佳的收斂速度和收斂精度。HLBPSO算法能夠以最少的尋優代數找到最佳的解，這是由于HLBPSO算法采用了分等級學習策略，不同等級粒子采取合適的學習策略，使得算法在收斂初期具有較快的收斂性能；當HLBPSO算法陷入局部最優的時候，在逃逸算子和慣性權重自適應更新策略的幫助下，使得算法跳出局部最優，增加解的多樣性，粒子繼續尋找更優解。

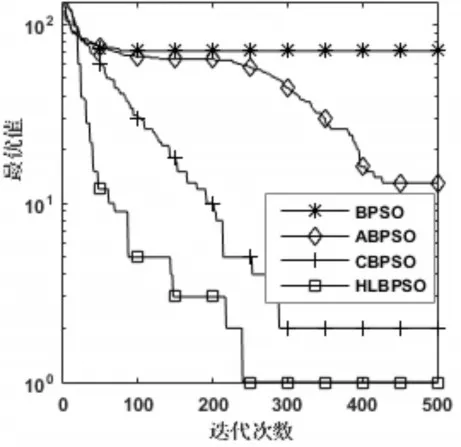
圖1 F1函數收斂曲線

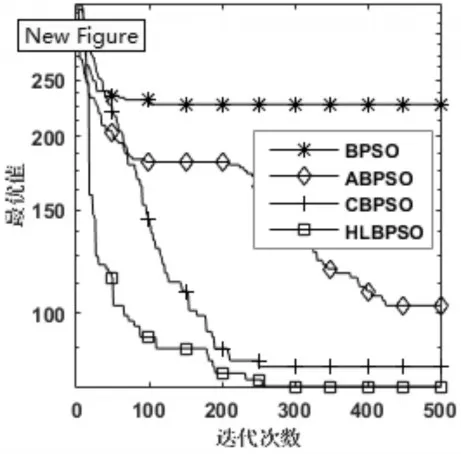
圖2 F2函數收斂曲線

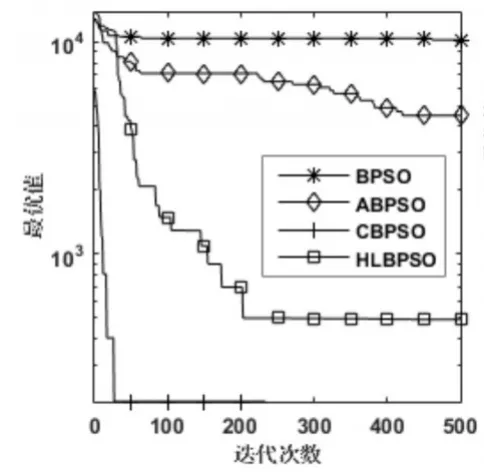
圖3 F3函數收斂曲線

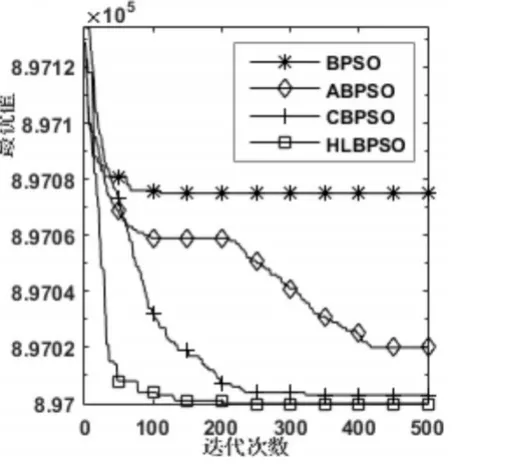
圖4 F4函數收斂曲線

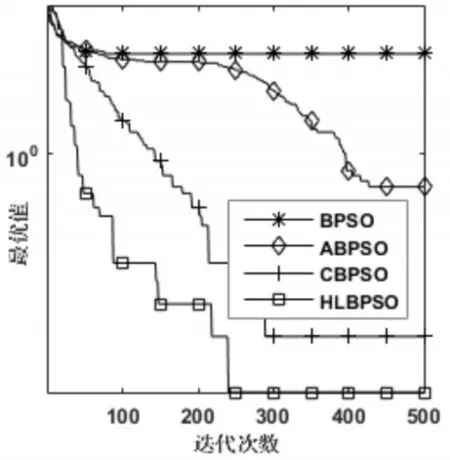
圖5 F5函數收斂曲線

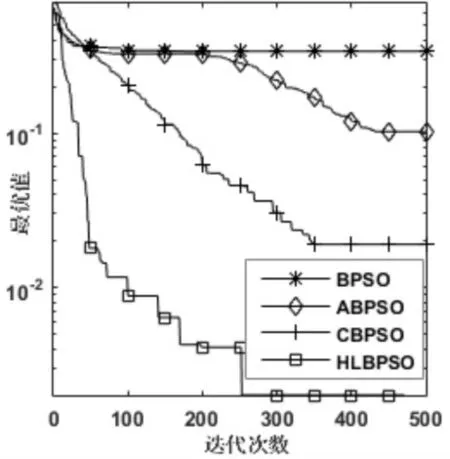
圖6 F6函數收斂曲線

5 結語

針對二進制粒子群存在收斂精度低、尋優后期多樣性丟失的問題，本文提出了采用分等級學習策略的HLBPSO算法。該算法針對不同等級粒子采用了不同的學習策略，并為劣勢等級粒子設計逃逸算子，最后根據當前粒子與優勢等級最優粒子間的歐式距離設計了慣性權重動態更新策略。實驗表明，本文所提HLBPSO算法具有較高的收斂精度和較好的魯棒性，分等級學習策略和慣性權重動態更新策略提升了算法跳出局部最優的能力，在一定程度上增加了解的多樣性。