一種基于鏈表的改進Apriori算法?

顧 鵬

（南京理工大學計算機工程與科學學院 南京 210094）

1 引言

隨著大數據時代的到來，關聯規則挖掘日益受到人們的重視，且在銀行、保險、電商、零售等行業的應用也越來越廣泛。作為關聯規則挖掘的經典算法，Apriori算法受到了廣泛的關注和研究。同時，利用Apriori算法挖掘頻繁模式也是構建商務智能系統前期數據預處理和特征提取的重要技術手段之一。經典的Apriori算法需要多次掃描事務數據庫，候選-N項集通過頻繁-N-1項集的連接產生，生成大量候選集，進行了大量的無用計算，尤其在項目數較多的情況下，這種情況更加明顯。

針對Apriori算法的性能瓶頸問題，人們開展大量的研究對Apriori算法進行改進，以提高其效率。較有名的是FP-Growth算法［17］，該算法采用樹和鏈表的混合結構，只需掃描兩次事務數據庫，且無需產生候選項集，但算法的局限性體現在頻繁的構造條件模式基，對于大規模數據集來講，FP-Growth算法所構建的FP-Tree會非常龐大，可能無法存儲于內存之中。

FP-Growth算法之所以高效，是因為采用特殊的數據結構將事務數據庫壓縮存儲到內存中，避免了重復掃描事務數據庫帶來的性能瓶頸。學者們也采用了其他的數據結構來對事務數據庫進行壓縮存儲，并在此特殊的數據結構上挖掘頻繁項集。文獻［3］提出用十字鏈表來壓縮存儲數據結構，文獻［7］首先將事務數據庫轉化為關系矩陣，并使用正交鏈表對該矩陣進行存儲，從而可以通過對鏈表節點集合進行操作實現頻繁項目集的挖掘。文獻［8～9］同樣采用特殊的方法壓縮事務數據庫，并通過各自特殊的方法挖掘頻繁項集。圖作為經典的數據結構，也被許多學者用到頻繁項集的挖掘中。文獻［6］將事務數據庫壓縮為一個有向圖進行存儲，有向圖頂點為項，邊為事務編號集合，通過對該圖的遍歷來搜索頻繁項集，與之不同是，文獻［1］采用以事務為頂點，項為邊的無向圖來存儲事務數據庫，在挖掘頻繁-K項集時，混合Apriori算法和基于圖的頻繁項集挖掘算法，在K較小時用Apriori算法，在K較大時用圖挖掘算法。文獻［4］分別用布爾矩陣（生成矩陣）和圖兩種結構來進行頻繁項集挖掘。文獻［2］采用PPC-Tree和N-list的數據結構，對項進行pre-order和post-order編碼，極大壓縮了事務數據庫，提高了算法的效率，文獻［15］混合利用Apriori算法和FP-Growth算法來挖掘頻繁項集。也有利用特殊的方法挖掘頻繁項集，以改進Apriori算法的效率，文獻［14］根據事務數據庫中事務的長度進行倒序排列，從最長的事務開始，求頻繁項集。

上述對Apriori算法的改進，均不同程度的提高了挖掘頻繁項集的效率，但算法采用的數據結構過于復雜，對事物數據庫的壓縮有限，對項集的支持度計數仍是采用循環或搜索統計的方法。本文在總結現有研究的基礎上提出了一種基于鏈表的改進的Apriori算法。該算法首先掃描事務數據庫計算頻繁-1項集并采用鏈表進行壓縮存儲，然后在頻繁-N項集（N≥1）的基礎上利用高效的位運算對鏈表進行合并操作生成頻繁N+1項集，并對頻繁N+1項集（N≥1）的產生過程進行了優化，提高了Apriori算法的效率。

2 IABL（An improved Apriori algo?rithm based on linked list）算法

2.1 算法描述

IABL算法首先掃描事務數據庫計算頻繁-1項集，并采用鏈表以垂直數據結構的形式將頻繁-1項集存儲在內存中，然后對頻繁-1項集鏈表中的節點進行兩兩合并生成頻繁-2項集鏈表。為節約內存，保存頻繁-1項集的Itemi和其支持度計數后，刪除頻繁-1項集鏈表，然后按相同的方法生成頻繁-N項集（N≥2），直到新生成的頻繁-N項集鏈表長度小于N，算法結束。具體步驟如下。

步驟1：加載數據，生成頻繁-1項集L1。掃描事務數據庫D，統計每個項目的支持度計數，獲得L1并采用如圖1所示的鏈表結構進行存儲。該鏈表包含兩種節點，Item節點和Tid節點。其中Item節點組成ILink鏈表，包含三個域，next指向下一個Item節點，如無則為Null，TLink域指向由Tid節點組成的鏈表，ID域存儲該Item節點包含項目的ID號；Tid節點中包含兩個域，rno存儲該項集在事務數據庫中出現的行序號，另一個為指向下一個Tid節點的next域，若無則為Null。TLink鏈表的長度，即所包含Tid節點的個數，為該項集的支持度計數。

步驟2：根據步驟1中生成的ILink鏈表，對IL?ink鏈表中的Item節點進行兩兩合并，生成新的Item節點，如果該節點的支持度計數滿足最小支持度計數，則將該節點添加到新的ILink中，否則丟棄。新的ILink中的所有節點均為頻繁-2項集。在節點合并時，一個節點只與其之后的節點合并，具體合并時，對于待合并的兩個節點Item1和Item2，合并生成一個新的Item節點NewItem，NewI?tem.ID=Item1.ID∪ Item2.ID，NewItem.TLink=Item1.TLink∩Item2.TLink。然后刪除頻繁-1項集的IL?ink鏈表，保存頻繁2項集的ILink中各個Item節點的ID和支持度計數信息得到L2。

步驟3：重復步驟2直到ILink的長度小于N為止。但在Item節點的兩兩合并過程中，需要增加以下判斷以減少不必要的計算。

1）判斷新生成的ID是否屬于N項集令║ID║為ID所表示的項集中所包含的項目的個數，如果║ID║≠N，進行下兩個節點的合并，否則進行下一步。

2）根據新生成的ID在ILink中查找是否已存在具有相同ID的節點，如果存在，則進行下兩個節點的合并，否則進行下一步。

3）判斷ID所表示的項集的所有長度為N-1的子集是否為頻繁集，如是則進行下一步，進行下兩個Item節點的合并。

2.2 算法分析

接下來采用表1所示樣本事務數據庫，對本文所提出的算法進行具體的描述，并對算法性能進行簡要的分析。設最小支持度計數為2。

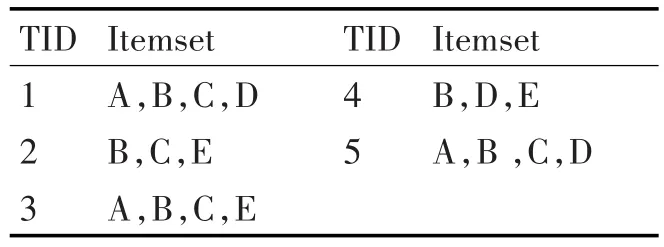
表1 樣本事務數據庫

1）根據IABL算法步驟1，掃描事務數據庫，計算頻繁-1項集L1，構建L1的ILink鏈表，L1=｛B，C，D，A，E｝，其支持度計數分別為：5，4，4，3，3。結果如圖2所示。

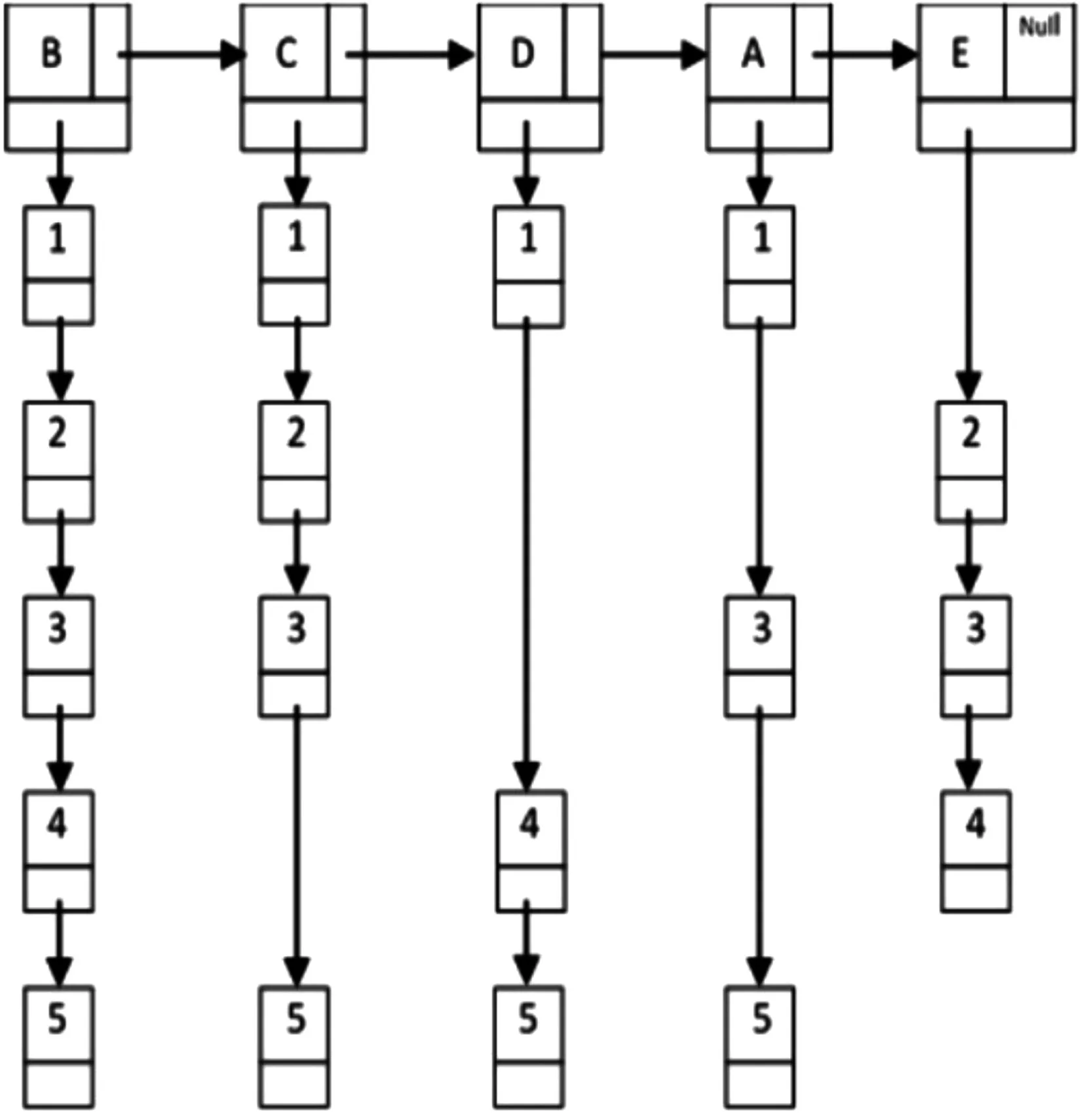
圖2 L1的ILink

2）按步驟2，對1）生成的ILink中各Item節點進行兩兩合并，由滿足條件（支持度計數不小于最小支持度）的新生成的Item節點構成L2的ILink，其結果如圖3所示。根據L2的ILink結果，可得到L2=｛BC，BD，BA，BE，CA，CD，CE，DA｝，其支持度計數分別為4，3，3，3，3，2，2，2。

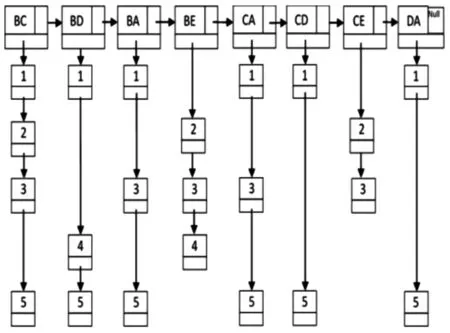
圖3 L2的ILink

3）按步驟3，對步驟2中生成的ILink進行兩兩節點的合并，結果如圖4所示。根據L3的ILink，L3=｛BCD，BCA，BCE，BDA，CDA｝，其支持度計數均為2。同樣地，可得到L4的ILink，其結果如圖5所示。可得到L4=｛BCDA｝，其支持度計數為：2。因此時IL?ink中Item節點的個數少于4個，算法結束。

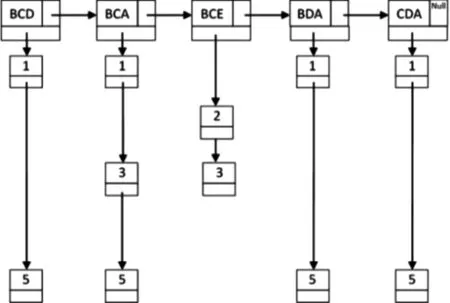
圖4 L3的ILink

根據上述采用表1的樣本事務數據庫對算法的具體描述可以看出：

圖5 L4的ILink

1）本算法采用鏈表結構對事務數據庫進行一次掃描后存儲到內存中，避免了多次掃描事務數據庫帶來的頻繁I/O操作，解決了Apriori算法的性能瓶頸問題，同時本算法采用的用嵌套鏈表存儲事務數據庫的方法，客觀上對事務數據庫信息進行了壓縮，數據量越大越稀疏壓縮效果越明顯。

2）在頻繁項集的迭代生成過程中，LN的生成，包括項集支持度計數的計算只與LN-1相關，方便計算的同時整體上減少了內存開銷。

3）算法采用鏈表結構存儲事務數據庫信息，在生成頻繁項集的過程中只進行兩個Item節點的合并操作，方法簡單，實現容易，但克服了經典Apriori算法的瓶頸，提高了頻繁項集挖掘的效率。

為了提高算法的運行效率，可將高效的位運算運用到兩個Item節點的合并過程中，包括其ID域和Tid鏈表的合并（實際上是兩個Tid鏈表求交集），具體方法如下：

1）ID域的合并。首先對L1中的所有項進行編碼，用與L1中項的個數相同長度的二進制位對L1中的每個項進行編碼。如在上面的示例中，L1=｛B，C，A，E｝，則我們可以用4位二進制位來對L1中的每個項進行編碼，具體為：B=1000，C=0100，A=0010，E=0001，在ID域的合并過程中則直接對其編碼進行或運算，如B∪ C=1000|0100=1100。

2）Tid鏈表的合并。類似地，如對于圖3中Item節點B的Tid域可以表示為：11111，C的Tid域可表示為：11101，對節點B和C的Tid域進行合并操作，計算11111&11101即可。支持度計數的計算只需求11101中“1”的個數即可。

3）需要注意的是，如果L1中的項的個數較多，或者事務數據庫中事務的數目較多時，可以采用鏈表等方式來處理。如事務數較多，可將事務劃分為若干塊，每塊設置編號，在塊內依然用二進制串表示，以便可以用高效的位運算來進行兩個Item節點的合并。

3 實驗分析

為對IABL算法的性能進行驗證，采用Java編程語言將該算法與FP-Growth算法的性能進行了實驗對比分析。實驗環境為華碩X556UB筆記本電腦一臺，配置如下：CPU Intel（R）Core（TM）i7-6500 2.5GHz；8G內存；64位windows 10操作系統，數據集共6組，詳情如表2所示。

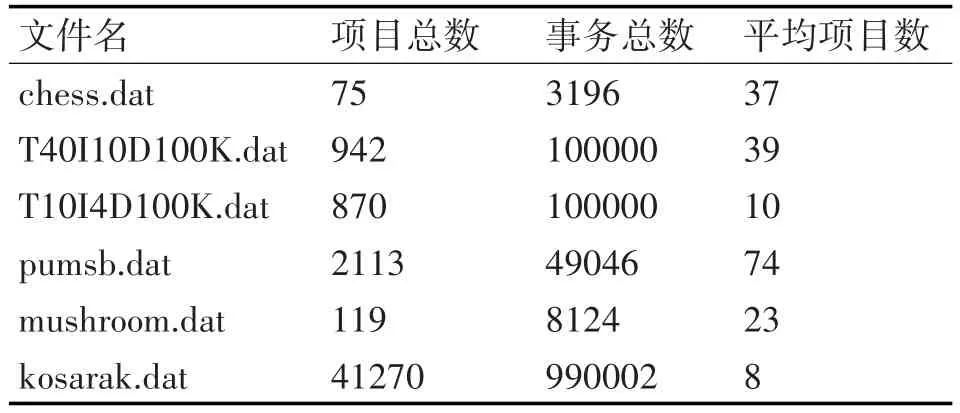
表2 實驗數據集詳細信息表

表2中T40I10D100K.dat、T10I4D100K.dat兩個數據集為采用IBM Quest Market-Basket Synthetic Data Generator生成的數據集，其余的數據集為真實數據集。在上述實驗條件下，分別用實現的兩種算法在6組數據上進行了實驗，具體實驗結果如圖6～圖11所示。通過實驗結果數據綜合分析，可以得出如下結論。

1）總體上，IABL算法性能明顯高于FP-Growth算法。從所示各圖可以看出，對于相同的數據集，在相同的最小支持度時，IABL算法的執行時間明顯低于FP-Growth算法的運行時間。

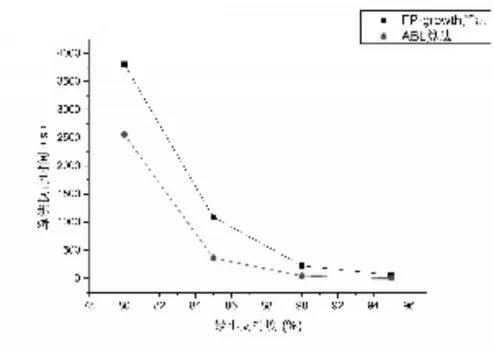
圖6 chess數據集

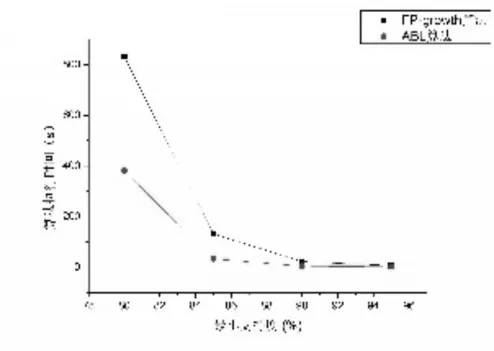
圖7 pumsb數據集

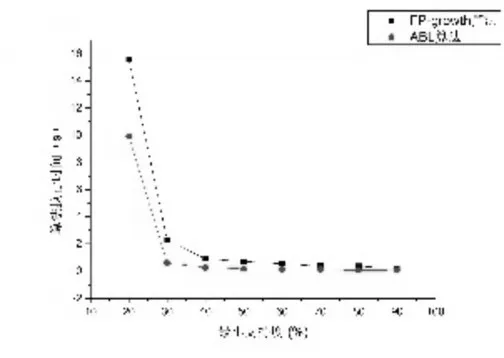
圖8 mushroom數據集

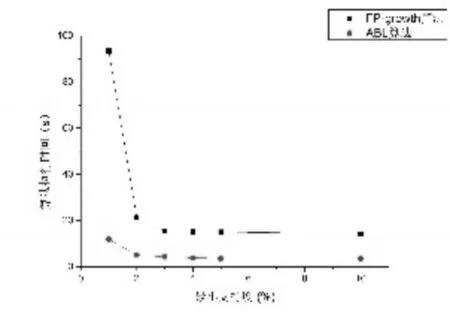
圖9 kosarak數據集

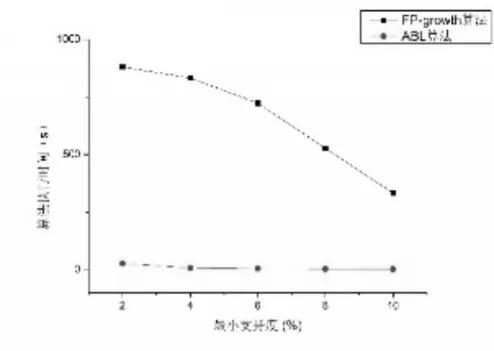
圖10 T40I10D100K數據集

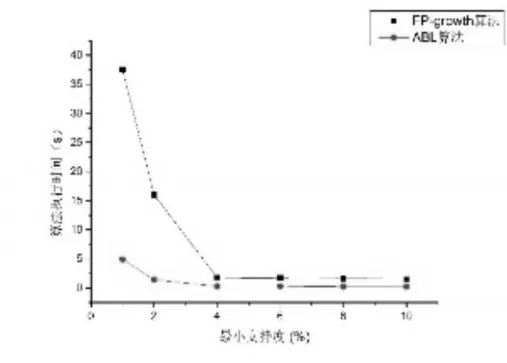
圖11 T10I4D100K數據集

2）對同一數據集，隨著最小支持度的降低，IABL算法和FP-Growth算法在同一最小支持度下的運行時間差距更大。如圖6所示，當最小支持度為95%時，IABL算法與FP-Growth算法各自運行時間所表示的點在圖上幾乎重合，但當最小支持度降低到90%時，我們可以清楚地從圖上看到差距，而當最小支持度降低到85%時，這種差距更明顯。對同一數據集而言，最小支持度越小，所得到的頻繁-1項集也就越多，意味著有更多的項參與到之后的頻繁-2項集以及頻繁-N項集的計算中，計算的復雜度也會相應的增加。這也說明IABL算法在查找頻繁項集的計算中效率要高于FP-Growth算法。

3）IABL算法在低密度數據集上的性能表現相較于FP-Growth算法優勢更加突出。如圖6～圖11所示三個數據集，其特點就是數據密度低，數據量大。如kosarak.dat數據集，項目總數為41270，而平均事務長度只有8，事務總數卻達到990000。根據算法的實現原理，以圖4～6所示的兩種算法在T10I4D100K數據集上運行結果對比為例，對其原因進行分析。

當最小支持度為10%時，數據集中滿足最小支持度的項的個數為0，算法運行時間的差距較小，產生差距的原因在于對數據的讀取和計算頻繁-1項集上。

當最小支持度降為4%時，頻繁-1項集的數目為26，而頻繁-2項集的數目為0。FP-Growth算法的運行過程為：根據得到的頻繁-1項集開始第二次掃描事務數據庫構建FP-Tree［4］，然后根據構建的FP-Tree調用FP-growth（Tree，α）挖掘出所有頻繁項集。IABL算法的運行過程為：掃描事務數據庫得到頻繁-1項集并構建ILink鏈表，然后對TidLink鏈表采用位運算的形式進行兩兩合并，并計算其支持度計數，確定頻繁-2項集，頻繁-2項集為空，算法結束。由于FP-Growth算法需要掃描兩次事務數據庫，而IABL算法只需掃描一次事務數據庫，同時構建FP-Tree和之后的挖掘頻繁模式也比IABL算法計算更復雜，效率更低。實驗結果也很好地驗證了這點，在最小支持度為4%時，在T10I4D100K數據集上，FP-Growth算法的運行時間為1968ms，而在同等的條件下，IABL算法的運行時間為422ms，是FP-Growth算法的21.44%。

當最小支持度為1%時，頻繁-1項集的數目是375，頻繁-2項集的數目為9，頻繁-3項集的數目為1。為了挖掘出所有滿足最小支持度的頻繁項集，FP-Growth算法需要對查找出的375個頻繁項構建龐大的FP-Tree，并在此基礎上展開對樹的搜索查找出所有的頻繁項集，這將是繁重的工作，必將耗費大量時間。而IABL算法基于查找出的375個頻繁項構建的ILink鏈表，一方面對數據進行了充分的壓縮，另一方面采用位運算迭代計算頻繁-2項集和頻繁-3項集，計算量相對較小，位運算的速度也比搜索操作的速度更快，從而整個算法的執行效率也就更高。實驗結果顯示，在最小支持度為1%時，在T10I4D100K數據集上，FP-Growth算法的執行時間為37546ms，IABL算法的執行時間為4947ms，是FP-Growth算法的13.18%。

4）綜合圖6～11及上述1）～3）的分析，相對于FP-Growth算法而言，由于采用特殊的ILink鏈表結構對預先計算出的頻繁-1項集進行了壓縮存儲，整個算法在挖掘頻繁項集的過程中只需掃描一遍事務數據庫，采用高效的位運算挖掘頻繁-N項集以及計算其相應的支持度計數，IABL算法性能明顯優于FP-Growth算法，在數據密度低的數據集上這種優勢更加明顯，其效率也更高。

4 結語

本文在研究總結現有關聯規則挖掘算法的基礎上，提出并實現了一種基于鏈表的改進Apriori算法，該算法使用嵌套鏈表對事務數據庫和前一頻繁項集LN-1進行存儲，并對經典Apriori算法的連接、剪枝和驗證過程基于嵌套鏈表的存儲結構進行了優化，并采用多個數據集對本文所提出的算法與經典的FP-Growth算法的運行結果進行對比分析，證明了本文提出的算法的可行性與正確性。通過實驗的對比分析，本文所提出的算法具有更好的性能。雖然算法能處理較大量的數據集，但內存空間畢竟有限，在今后的研究中將基于分布式和并行計算對算法進行改進，以適應更廣泛的應用需求。