背包模型結合粒子群算法的泵站節能優化?

劉慶華 陳文娟

（江蘇科技大學計算機科學與工程學院 鎮江 212003）

1 引言

水利工程的發展與建設，對于國民經濟的提升有著積極的促進作用，修建泵站并使得泵站高效運行在其中尤為重要［14］。泵站工程可以在很大程度上緩解洪澇干旱環境惡化等問題對于人民生活的影響，與此同時，泵站還具有投資成本低、工期短、見效快、易于實現自動化等優勢。我國泵站建設就現狀而言，屬于投資較少發展較慢的階段。據統計，大中型泵站的平均裝置效率僅為30%～50%，泵的耗電量約占全國總發電量的20%［1］。因此，對泵站節能消耗、優化管理等問題的研究尤為重要。我國沿江沿湖的平原地區大部分泵站的泵機都為可調節葉片的軸流泵，當給定了揚程和抽水流量之后，這類泵站可通過調節水泵的葉片角度，控制水泵的流量，并合理確定開機臺數，通過機組問的優化組合，使整個泵站的能耗最少，達到整體最優、經濟運行的目的［2］。

就目前國內外的研究現狀來看，泵站的優化主要是對泵站的機組運行工況的調節和泵站運行方式的優化調節。汪安南運用動態規劃的數學方法進行求解的數學模型［3］。周龍才等在采用迭代法求解泵組工作參數的基礎上［4］，建立了求解多并聯泵組最優開機組合的動態規劃模型。龔懿等提出基于二級子系統實驗選優的大系統二級分解-動態規劃聚合法［5］。Ormsbee提出二級優化策略，第一級優化蓄水池的最優水位變化曲線，第二級優化水泵的最優組合，Kevin E.Lansey等在此基礎上，采用了動態規劃求解［6］。目前的研究現狀顯示，研究多著重于優化約束條件、數學模型以及算法，且效果顯著有較大的上升空間。

泵站的優化模型中需要對多個參數進行約束，對于條件約束通常采用罰函數［7］進行處理，限制不滿足約束條件的數值出現的概率以達到優化效果。背包問題［8］屬于典型模型優化問題，在實際生產工程中得到較為廣泛應用。劉敏忠等［9］將電力系統負載恢復問題進行建模，使其成為具有多個約束條件的背包問題，從而確保了系統恢復的安全性；王炎娟等［10］將多衛星偵察成像任務以及各種約束條件類比成背包問題中的“物品”和“背包”，從而建立多維動態背包模型；董鑫等運用背包模型來解決油庫人員在各個崗位上的最佳分配問題［11］。將泵站的優化約束轉換為背包的重量約束，而不是罰函數，可以避免罰函數選擇的不確定性，簡化優化模型。

人工智能算法正在日趨成熟，已經逐漸被應用于解決泵站優化問題中。Jalali M R［12］等使用改進的蟻群算法使其高效地處理離散決策變量和連續決策變量組合的優化問題，從而解決了蟻群優化算法對于連續空間中性能較差的問題。Milan Cisty提出結合遺傳算法（GA）和線性規劃（LP）方法來解決供水系統的最優問題［13］。

本文分析了泵站經濟運行數學模型，以常熟水利樞紐望虞河站為例，根據泵站總耗能最小原則，分析了泵站間和站內經濟運行，將泵站優化模型轉化為背包模型，采用粒子群對開機方案進行求解，得出在特定水情之下的優化開機組合。

2 水利泵站運行理論模型

泵站實現優化運行主要是對泵站的單元機組系統進行全面的分析和比較，使泵站在最節能的工作條件下運行。即根據某些最佳標準并且在滿足規定約束條件的前提下，使泵站優化運行的數學模型中目標函數值達到最值。本文主要從能耗最小和效率最高兩方面來考慮優化泵站，即總的抽水量規定好的的前提下，使各泵機的抽水量總和大于規定的抽水量時泵裝置的運行功率最小且功效最大，泵機的抽水量可以通過改變泵機葉片的角度進行調節。

1）目標函數

泵站運行時的耗電量較大，在不考慮時間因素的條件下，m臺水泵最小消耗功率的數學模型表達式為

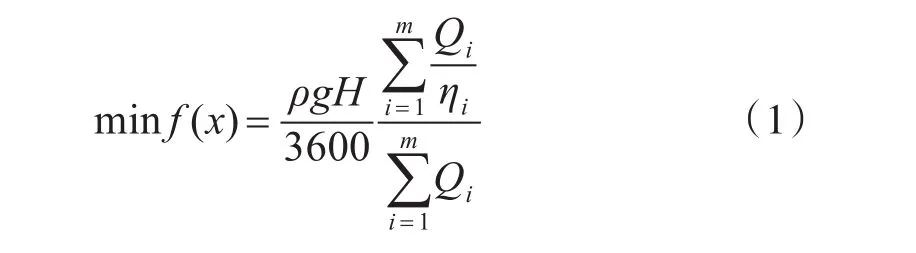
式中：i為泵的序號；ρ為水密度，1000Kg/m3；g為重力加速度，9.8m/s2；Qi為第i臺泵的流量，m3/s；H為第i臺泵的揚程，m；ηi為第i臺泵的效率。

2）約束條件

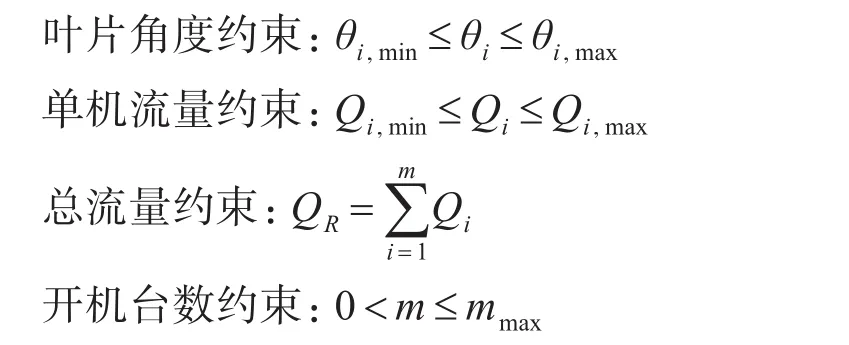
3 背包模型轉化

背包具有容量上界，一個0-1背包相當于一個集合，該集合包含了若干項物品，每項物品都有其重量和效益值［19］。背包問題的目的在于：選擇適當的物品子集，在滿足物品重量總和不超過背包容量上界的前提下，使得所選中的物品效益值總和最大化［20］。背包問題是一個典型的組合優化問題，在實際應用中，資源分配、資金運算、組合優化等問題都可抽象為背包問題，本文嘗試將泵站優化問題轉化為背包問題。

1）目標函數轉化

大型泵站工程中都傾向于使用軸流泵機組，該種類型的泵機屬于葉片角度可調節型，合適的葉片角度可以使泵機達到運行最優。將每臺軸流泵的葉片角度可調范圍按一定間隔進行離散，計算出各個角度離散點對應的水泵運行的流量、效率等。每個角度離散點作為一個“物品”，計算出功率值，即為該物品的“價值”。根據背包模型中物品總價值最大的原則，則目標函數轉化為

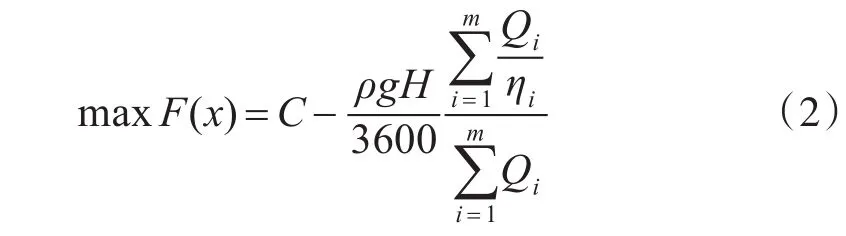
式中，C為保證F為正值的一極大常數。

2）約束條件轉化

開機的臺數和單泵的葉片角度可通過算法編碼實現，每臺泵每個角度離散點的流量值可計算得到，當此水泵停機時，流量為0，當開機時，流量即為計算值，故單泵流量約束也可自動滿足。設背包總重量為M，在滿足流量要求的前提下，單個物品的重量為

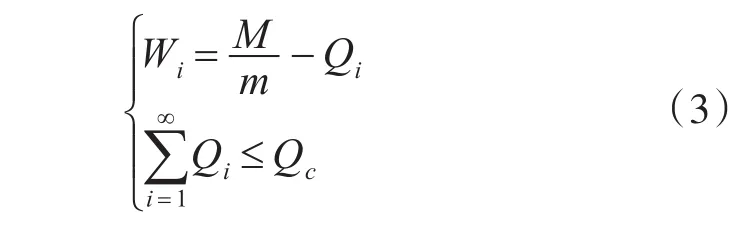
綜上可得放入背包的所有物品的總重量應滿足：

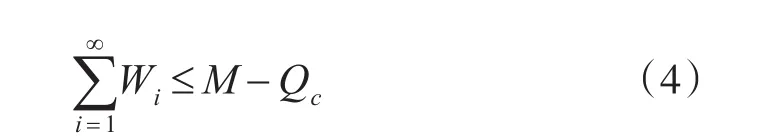
其中，M大于每臺機組以最大流量運行時泵站的總流量。

4 背包模型結合粒子群算法優化

粒子群優化算法是受鳥群覓食行為的啟發而提出的［21］，采用種群中的全局搜索最優的方式，將其簡化成個體與群體的速度位置模型，從而避免較為復雜的遺傳過程。另外，它特有的記憶使其可以動態跟蹤當前的搜索情況來相應調整其搜索策略，具有較強的全局收斂能力和魯棒性［22］。

在粒子群優化中，D維空間的每個“粒子”都代表了優化問題的可行解決方案，在整個優化過程中，每個粒子的適合度取決于其優化函數的值的選擇，并且每個粒子具有以下類型的信息：粒子的當前位置，在飛行過程中根據經驗得出的最優位置、群體中同伴共享經驗的最佳位置。每個粒子通過自身最優位置和群體最優位置來影響飛行中的速度和位置，從而使得粒子本身和群體都趨于最優。

設在D維空間中有n個微粒，第i個微粒在空間中的位置Xi、速度Vi以及經歷的歷史最好位置Pbest分別為

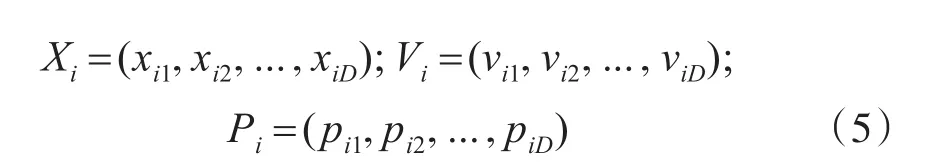
式中i=1，2，…，n，每一個微粒都有與優化目標函數相對應的適應度值，一般以優化函數作為適應度值函數。整個種群中微粒所經歷過的具有最好適應度值的位置為gbest=（g1，g2，…，gD）。函數：

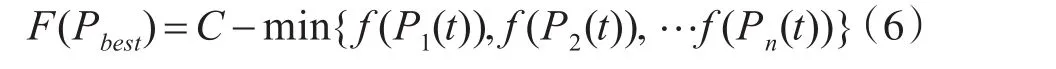
表示全局最優解。對第t代的第i個微粒，粒子群算法根據下列進化方程計算第t+1代的第j維的速度和位置：

其中：w為慣性權重，c1和c2為加速常數，rand1和rand2為兩個在［0，1］范圍內變化的隨機函數。此外，粒子的速度Vi被一個最大速度Vmax所限制。若此刻增加粒子的運動速度，從而使得在某個維度該速度已經超過了粒子的最大速度，則該速度會代替原本的速度成為該維度的最大速度。

該算法的迭代終止條件通常是最大迭代次數或到目前為止由粒子群搜索的最佳位置的適應度值，可以滿足預定的最小適應度閾值。因為粒子都根據自己的經驗和小組經驗不斷地接近最佳解的方向，所以當所有粒子都到達同一點時，可以認為已達到最佳位置。

粒子群算法求解最優化問題的算法流程：

1）設定粒子群粒子個數、尋優代數、加速因子、慣性權重系數等參數值，隨機初始化各粒子的位置和速度；

2）由所要優化的目標函數的設計變量數確定粒子的空間維數，由目標函數值計算每個粒子的適應度值，并計算 Pbest和 gbest；

3）比較每個粒子的適應度值與個體極值Pbest，如果f（Pi）>f（Pbest），則Pbest=Pi

4）比較每個粒子的適應度值與全局極值gbest，如果f（gi）>f（gbest），則gbest=gi

5）更新單個粒子的飛行速度和空間位置；

6）判斷是否滿足收斂條件，若未達到返回步驟2）繼續尋優，若達到則停止尋優，并輸出計算結果［23］。

本文基于常熟某大型水利泵站的實際工況數據，在優化模型的基礎上擬合出水利泵站性能曲線，得到擬合公式后利用粒子群算法尋優，求解出在特定水情之下的優化開機組合。具體流程見圖1。

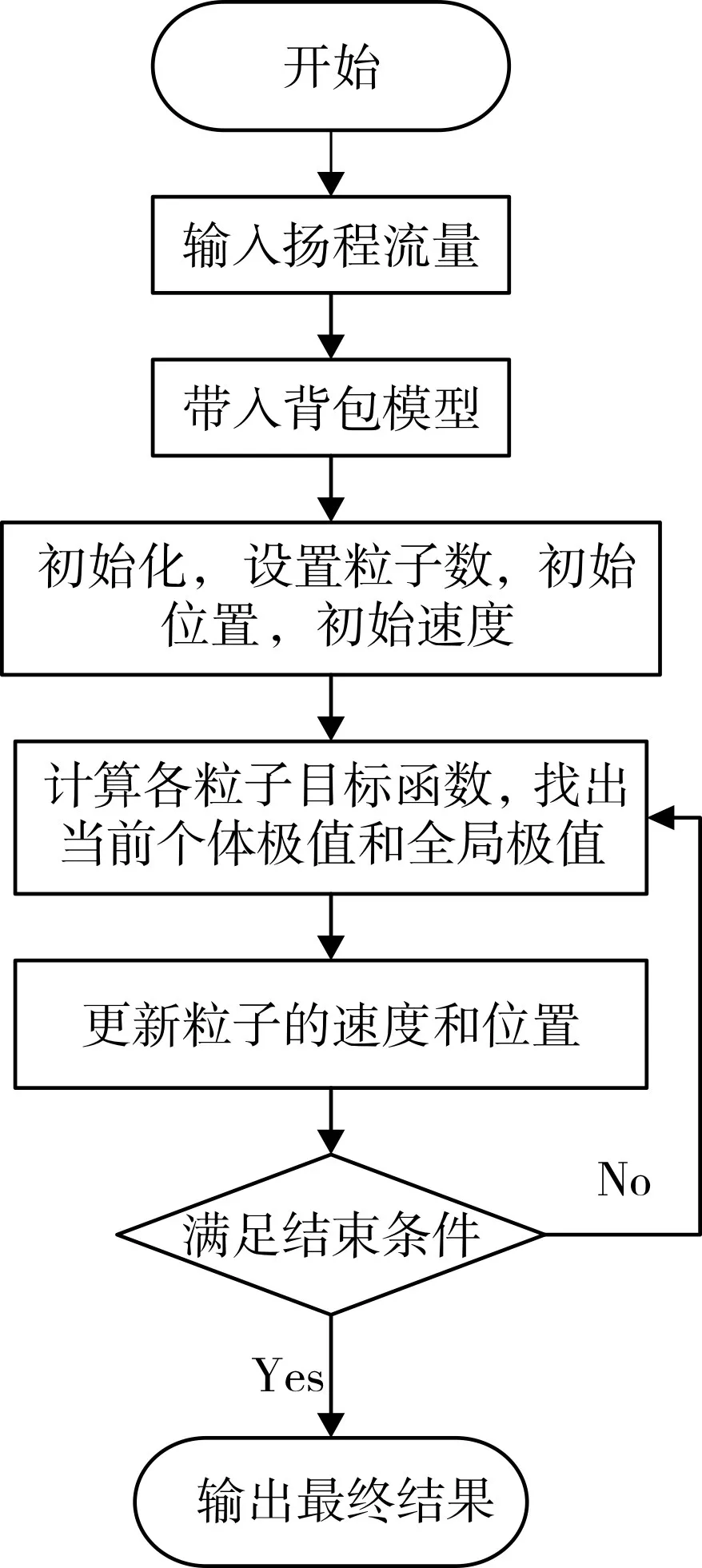
圖1 本文方法流程

5 實驗及分析

5.1 水泵綜合性能曲線擬合

本文通過對各種工況下的數據進行分析處理，擬合出各個工況下的葉片角度與功率、流量、揚程之間的關系方程，從而精確計算泵站中每臺泵機在運行過程中的能耗值，通過不同角度的組合達到能耗值的最優。本文以江蘇常熟水利樞紐望虞河泵站為研究背景，基于望虞河泵站2500ZLB20-1.75型開敞式軸流泵進行了數據擬合，該泵站所采用水泵葉片均可在-4°、-2°、0°、2°、4°離散調節，采用的TJ-04-23泵機組模型［19］。

模型與測試試驗數據由揚州大學與江蘇大學提供，模型泵葉輪直徑300mm，模型比λ=1∶8.333，模型在上下兩層流道前后開設了4個觀察窗，以0°角度為例，按照模型比λ=1∶8.333進行換算，可以得到實際泵裝置的工況點數據，該模型的能量試驗數據如表1所示［19］。

利用Matlab的數據擬合工具箱，實現以上數據的分析擬合。得出流量-功率、揚程-流量的擬合曲線。如圖2、3所示，未葉片角度未0°時的關系曲線：

同理對其他各個角度的關系進行擬合，得到表2各角度擬合曲線公式。

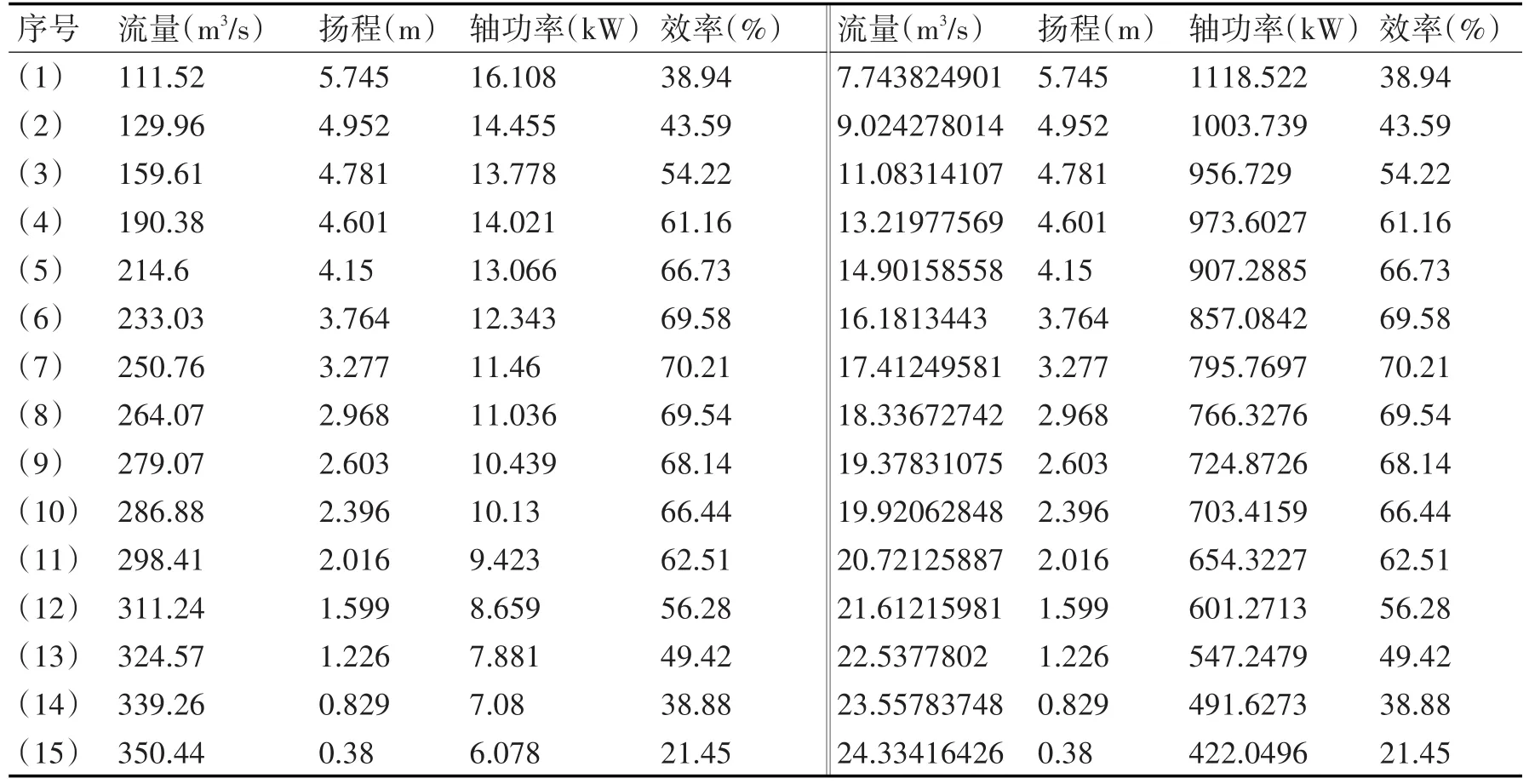
表1 0°能量試驗數據及換算后裝置實際工況點數據

5.2 粒子群算法求解泵站經濟運行開機方案

上文曲線擬合出的性能公式，通過粒子群算法對其進行進一步的尋求搜索。主要依照如下的步驟進行：

1）確定各運行參數及其取值范圍，如最大迭代次數、速度和位置的運動范圍、慣性權重、泵機開機型號、開關機臺數限制、水泵轉速限制等。

2）初始化種群和泵站數、泵機數、粒子群規模、單個粒子的速度和位置，其中粒子的位置與泵機組的開機型號、臺數和轉速比相對應。

3）根據擬合出的的流量～揚程性能曲線方程，計算出當前每臺泵機的流量和功率，通過背包模型轉化的目標函數計算粒子的適應度函數值F（Pi），并計算個體極值F（Pbest），、全局極值F（gbest）。當此水泵停機時，流量為0，當開機時，流量即為計算值，故流量約束也可自動滿足。

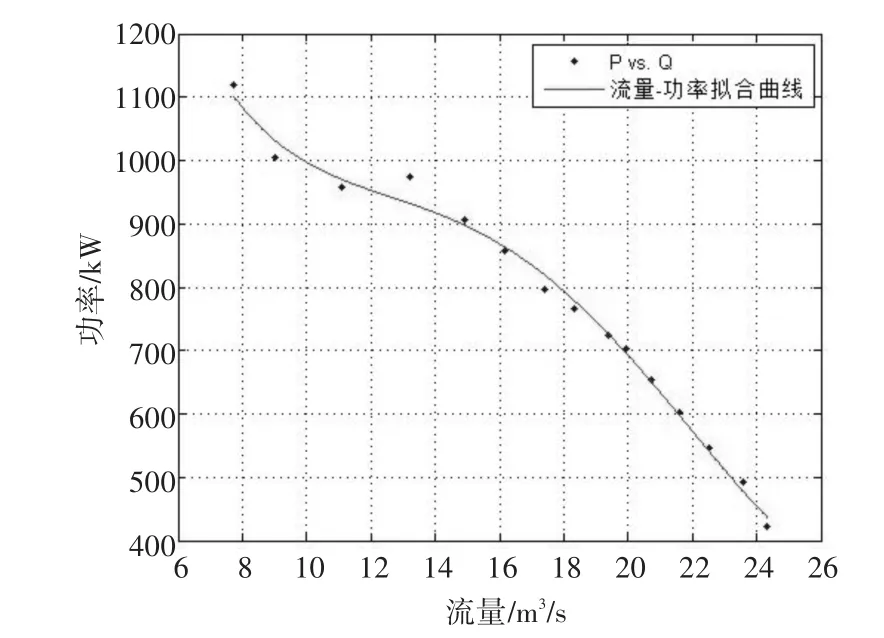
圖2 0°流量-功率擬合曲線圖

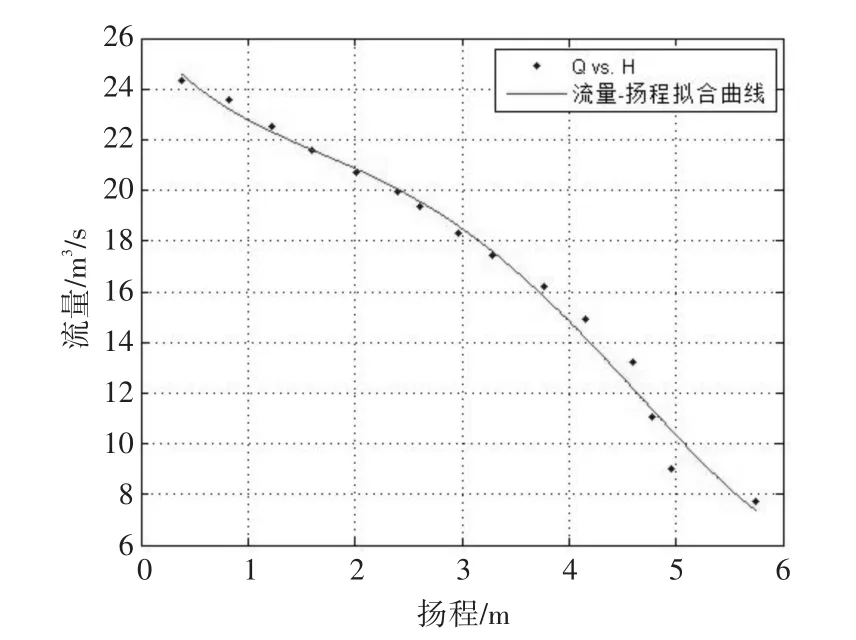
圖3 0°流量-揚程擬合曲線

表2 各角度擬合曲線公式

4）根據擬合出的的流量～揚程性能曲線方程，計算出當前每臺泵機的流量和功率，通過背包模型轉化的目標函數計算粒子的適應度函數值F（Pi），并計算個體極值 F（Pbest），、全局極值F（gbest），當此水泵停機時，流量為0，當開機時，流量即為計算值，故流量約束也可自動滿足。

5）比較每個粒子的適應度值F（Pi）與個體極值F（Pbest），如果 F（Pi）>F（Pbest），則 Pbest=Pi。比較每個粒子的適應度值與全局極值 gbest，如果 F（Pi）>f（gbest），則gbest=Pi。

6）更新每個粒子的速度和位置。

7）根據結束條件來判斷是否可以結束，或者誤差是否達標，或者是否以及達到了最大循環次數。若滿足則結束流程，若不滿足循環到滿足條件后結束流程。

6 結果分析

為驗證背包模型的可行性及粒子群算法的有效性，對上述泵站進行優化計算。泵站靜揚程3m，需要流量為140m3/s。在模型求解中，將粒子種群數設定為300，終止迭代精度設為0.001，最大迭代數設定為500，粒子速度范圍設定為［0.1，1），慣性權重設定為0.95，且以線性變化到0.4，并將最大迭代次數作為算法停止的條件。

根據不同葉片角度下的能耗，擬合出的水泵工況點數據，和不同葉片角度下的功率與流量、揚程的性能方程，采用粒子群算法進行優化計算，并與傳統的遺傳算法進行比較，如圖4所示。

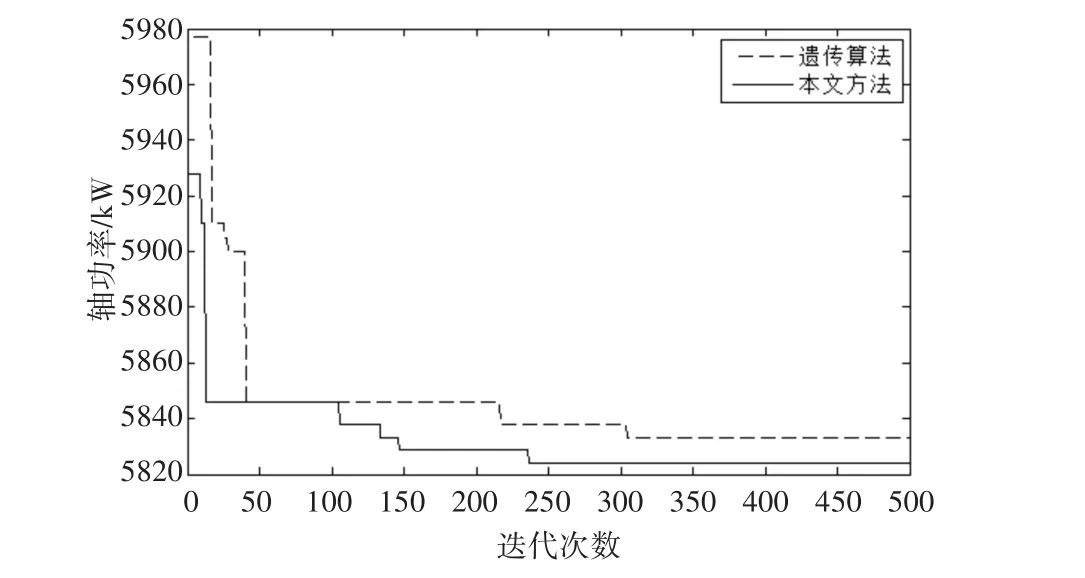
圖4 方法對比圖

由圖可知，本文背包模型粒子群算法能找到泵站優化運行的最優解，并且與傳統數學模型遺傳算法結果一致，說明將泵站優化問題轉化為背包模型進行求解是可行的。且本文方法在計算過程中所需迭代的次數比標準遺傳算法少，且最終的收斂結果更優。

若按照傳統數學模型，僅將達到流量的開機組合確定為開機方案。根據泵機組的分布可知，當運行中的泵機組對稱分別時，可以更穩定的過流，故驗證開啟共8臺機組，均以0°葉片角度運行。未優化與兩種優化算法計算結果如表3所示。

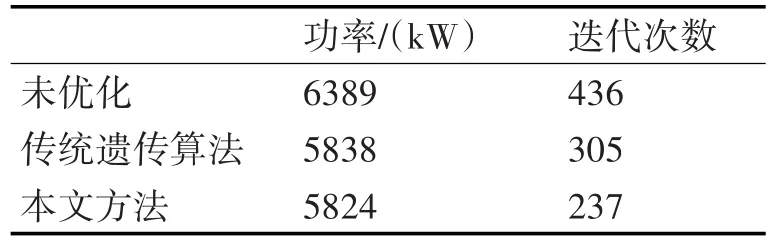
表3 不同方法的性能對比

由表3可知，采用優化算法泵站計算出的功率更低需要的迭代次數更少。而粒子群算法相比于傳統的遺傳算法，功率下降0.2%，迭代次數也降低了2.2%，效率更高。優化后泵站運行方式如表4所示。在此揚程及流量條件下，可根據優化方案進行水泵開、停機及葉片調節。

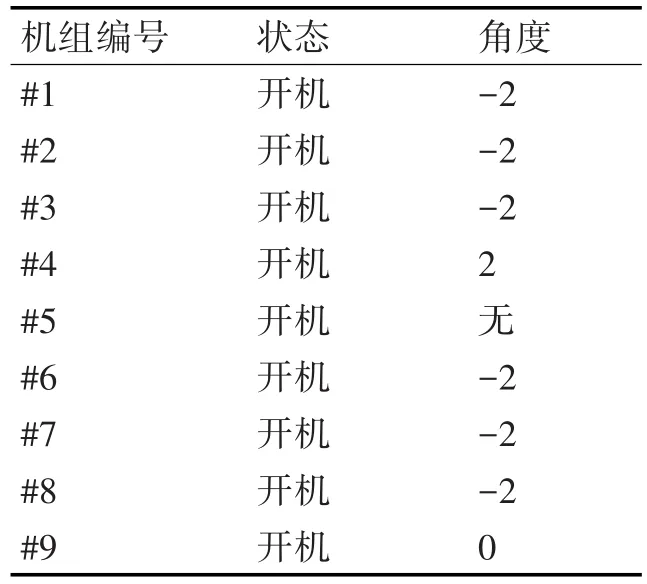
表4 泵站優化運行結果

7 結語

水利泵站的優化是具有約束條件的組合優化問題，本文嘗試采用背包模型優化方案解決該問題。背包的重量函數用于代替懲罰函數以簡化優化模型。根據實驗結果可得，基于背包模型的優化粒子群算法可以找到泵站的最佳運行方式并與傳統數學模型的結果吻合，表明使用背包模型解決泵站優化問題是可行的。優化抽水站后，可以優化抽水站的運行方式，提高抽水站的效率，降低能耗，達到節能的目的。本文中的工況的優化是靜態優化。在實際項目中，有必要結合泵站信息和自動化系統具體分析，根據泵站在不同環境下所需要流量進行實時優化，并自動控制泵機開關機以及葉片角度調節動作。此外，泵站的流量和揚程變化較為頻繁而一般的優化計算方法速度較慢的問題，還可以引入人工神經網絡進行訓練和學習，尚需要進行深入的研究。