基于雞群優化算法的PID參數優化?

彭 健 曹中清

（西南交通大學機械工程學院 成都 610031）

1 引言

PID控制器具有結構簡單、魯棒性好、適用性強的特點，是目前工業生產過程控制中運用極為廣泛的控制策略之一［1］。PID參數是PID控制器中的核心，對于PID參數的整定，許多學者進行了各種各樣的研究，其中基于群智能算法［2］的PID參數整定方法收到了良好效果。文獻［3］提出了一種基于遺傳算法的PID參數優化方法，與Z-N方法整定的PID參數相比，系統具有更小的振蕩幅度和更短的振蕩時間；文獻［4］提出了一種改進遺傳算法優化PID參數的方法，與基本的遺傳算法相比，有更高的收斂速度和收斂精度；文獻［5］提出了一種基于改進的粒子群算法的PID參數優化方法，解決了PSO易陷入局部最優的問題，提高了算法的尋優能力。文獻［6］則對粒子群算法做了另一種改進，利用改進PSO優化后的PID控制器具備更強的抗干擾能力。文獻［7］使用人群搜索方法整定PID參數，精度和收斂速度都優于PSO方法。文獻［8］則對人群搜索方法做出改進，搜索速度和精度比傳統人群搜索方法又有提高。得益于群智能算法的發展，利用群智能算法優化PID參數的方法層出不窮［9～12］。本文提出了一種基于雞群優化算法的PID參數優化方法，通過Matlab仿真后的結果顯示，與遺傳算法和粒子群算法相比，本文方法具有更高的控制精度和更強的魯棒性，體現了其優越性和有效性。

2 PID控制器

PID（Proportion-Integration-Differentiation）控制器由比例單元P、積分單元I和微分單元D構成，主要用于對基本線性和動態特性不隨時間變化的系統進行控制。對于不同的控制過程需要選定相應的控制參數，否則控制器將達不到預期的效果［13］。

PID控制器的偏差e（t），由系統輸入rin（t）和系統輸出yout（t）構成：

PID控制器的輸出為

在計算機系統中，需要對PID控制器輸出進行離散化：

式中，Kp為比例系數Ti為積分時間常數，Td為微分時間常數，Ts為采樣時間。PID控制器輸出增量式的表達為

3 基于雞群算法的PID控制器

3.1 雞群優化算法

雞群優化算法（Chicken Swarm Optimization，CSO）是Meng Xianbing等于2014年提出的一類基于群體智能的隨機優化算法［14］。雞群被分為公雞、母雞、小雞三類角色，每只母雞隨機跟隨一只公雞，每只小雞隨機跟隨一只母雞，跟隨關系保持數代，公雞領導自己群體內的母雞和小雞與其他公雞進行競爭，數代之后重新分配公雞、母雞、小雞角色。經過數次迭代，選出最優的雞群中最優的個體，即為問題的最優解。

雞群優化算法流程具體如圖1。

圖1 雞群算法流程圖

3.2 算法的實現

3.2.1 參數的編碼

設雞群P中的個體的總數量為N，每個雞群個體的位置矢量由PID控制器的比例、積分、微分三個控制參數構成，個體位置矢量的維數D=3，例如，第n只雞的位置為ω3||e()

t)dt，e(t)<0。整個雞群的位置可以用一下矩陣來表示：

e(t)<0參數的取值范圍可以根據具體工程背景來決定，雞群的初始位置在相應的取值范圍內隨機生成。

3.2.2 適應度函數的選取

為了獲取滿意的過渡過程動態特性，采用誤差絕對值的時間積分性能指標作為最小目標函數。為了防止控制能量過大，引入控制輸入平方項，目標函數為

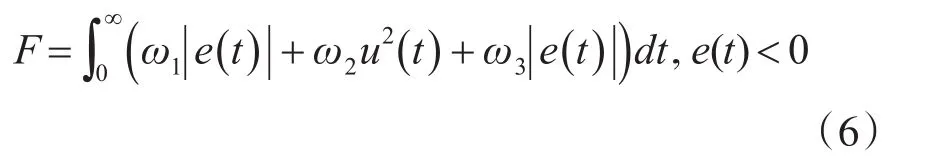
其中，e（t）為系統輸入rin（t）和系統輸出yout（t）之間的誤差值，u（t）為PID控制器的輸出，將這一項加入適應度函數的目的是避免控制幅度過大，ω1和ω2為權重，取值范圍為［0，1］。

另外，為了避免超調，在目標函數中引入了懲罰項，當出現超調時，誤差值會被劇烈放大，出現超調時的目標函數為［15］

其中，ω3為懲罰項的權重，且ω3>>ω1，，一般情況下，權重取值ω1=0.999，ω2=0.001，ω3=100。

3.2.3 雞群個體運動范圍的確定

對于雞群個體中位置矢量的每一個維度，雞群優化算法只允許雞群個體在給定的范圍內運動。在迭代搜尋的過程中，如果雞群個體的位置矢量超出給定的范圍，那么這些超出范圍的維度位置將被設置為邊界值。雞群個體遵循以下位置約束：

3.2.4 雞群個體的更新

在雞群個體更新的過程中，遵循以下規則：

1）在迭代開始時以及每經過若干次迭代時，將雞群所有個體按照適應度從優到劣的順序排列，適應度最優的若干個體設置為公雞，其次的若干個體設置為母雞，最差的若干個體設置為小雞。

2）母雞與公雞的跟隨關系、小雞與母雞的跟隨關系都是隨機的，跟隨關系保持若干代不變。在對雞群所有個體重新設置公雞、母雞、小雞角色時，跟隨關系會重新確立。

公雞的更新公式為

式中，randn是一個服從均值為0，方差為σ2的正態分布的隨機數。eps是一個很小的正數，為從所有公雞中隨機選取的個體的適應度值且k不等于i。為第t次迭代時，全局最優的個體。

母雞的更新公式為

式中，rand為服從［0，1］上均勻分布的隨機數，eps為一個非常小的正數，r為第i只母雞跟隨的公雞，h為其他母雞中隨機抽取的個體，且h≠i。

小雞的更新公式為

式中，m為第i只小雞跟隨的母雞，r為母雞m跟隨的公雞，C3和C4是服從［0，2］上均勻分布的隨機數，ω為慣性權重系數，它按照以下公式計算［16］：

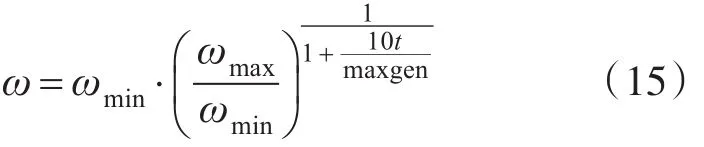
其中，t為當前迭代次數，maxgen為最大迭代次數。慣性權重ω可以影響雞群算法的局部最優能力和全局最優能力。較大的ω有利于提高雞群算法的全局搜索能力，而較小的ω會增強算法的局部搜索能力。

3.2.5 整定流程

基于CSO的PID參數整定原理如圖2所示。

圖2 基于CSO的PID參數整定原理圖

用于PID參數整定的CSO算法流程如下：

1）初始化雞群參數，隨機產生一個N×D的雞群矩陣。

2）根據公式計算雞群個體的適應度值，記錄最優個體位置和最優適應度值。

3）將雞群按照適應度優劣進行排序，給雞群分配公雞、母雞和小雞的角色。

4）根據公式更新公雞、母雞和小雞的位置并計算適應度，記錄雞群中最優個體位置和最優適應度值。

5）檢查是否達到最大迭代次數，是則進入步驟6），否則結束迭代并輸出最優個體和最優適應度值。

6）檢查是否滿足雞群角色更新條件，是則返回步驟3），否則返回步驟4）。

4 仿真結果及分析

4.1 控制對象及仿真條件設置

在過程控制中，許多系統常常被近似為一階或者是二階的典型系統，本文選取二階延遲系統作為控制對象，利用雞群優化算法（CSO）對系統PID控制器參數進行整定，并將其與粒子群算法（PSO）、遺傳算法（GA）、人群搜索算法（SOA）進行對比。選取的二階系統的傳遞函數如下：

對以上系統進行仿真，設雞群個體數量為60，公雞母雞和小雞的比例分別為0.2、0.4、0.4，最大迭代次數為100代；Kp，Ki，Kd三個參數搜索范圍為［0，100］；輸入信號為單位階躍信號，采樣時間間隔為0.001s，仿真時間為2s。四種算法各個參數的選取如表1所示。

表1 各算法參數設置

表1中，N為種群數量，w為慣性因子，wmax為權重上限，wmin為權重下限，Pc為染色體交叉互換概率，Pm為染色體突變概率，Umax為隸屬度上限，Umin為隸屬度下限。

4.2 仿真結果及分析

利用CSO、PSO、GA、SOA算法對選取的二階系統進行仿真，得到各個算法的適應度函數變化曲線和系統階躍響應輸出曲線分別如圖3和圖4所示。

圖3 適應度值變化曲線

從適應度值變化曲線可以看出，CSO算法的變化曲線下降速度和收斂代數都比另外三種算法要好，這說明CSO算法在收斂性上具有明顯優勢。

從系統階躍響應曲線可以看出，CSO算法的超調量比另外三種算法小，調整時間也比另外三種算法短，這說明CSO算法優化的系統穩定性要更好。

圖4 系統階躍響應輸出曲線

為了定量比較這幾種算法的優劣，結合以上適應度函數曲線和系統階躍響應曲線，選取了最小適應度值fmin、超調量Mp、調整時間ts（±2%）三項評價指標，并將幾種算法優化得到的PID參數一并羅列比較，如表2所示。

表2 各算法整定的PID參數及評價指標數值

從適應度值可以看出，CSO算法的精度高于其他三種算法，從超調量和調整時間上可以看出，相比于另外三種算法，經過CSO優化的系統超調量更小，調整時間也更短，能夠更快地進入穩定狀態。綜上所述，在PID參數整定上，CSO算法收斂速度更快，精度更高，其系統也具有更強的魯棒性，CSO算法具有明顯的優越性。

5 結語

針對PID參數的優化問題，本文提出了一種基于雞群優化算法的PID參數優化方法，并以二階時滯系統為例，使用Matlab軟件對其進行仿真實驗。仿真的結果表明，與基于GA、PSO和SOA的PID參數優化方法相比，本文方法具有更高的控制精度和更快的收斂速度，在優化PID參數的問題上具有優越性，可以為系統PID參數整定提供參考依據。可以預見，該方法在工業控制自動化方面會有不錯的應用前景。