時空軌跡相似度計算方法研究與實現?

涂剛凱 耿 鑫

（1.南京烽火天地通信科技有限公司 南京 210019）（2.武漢郵電科學研究院 武漢 430074）

1 引言

隨著衛星定位技術、無線通信、跟蹤檢測設備以及視頻實時采集技術的日益成熟，能夠方便人們低代價地獲得時空軌跡數據。針對時空軌跡的的研究也是層出不窮，比如軌跡聚類、路徑預測、興趣區域推測等。如何利用時空軌跡數據，深度挖掘出時空軌跡特征屬性，成為了工業界和學術界的熱點問題。唐爐亮［1］等提出了一種基于車載GPS軌跡數據的路網拓撲自動變化檢測新方法，魏爭爭［2］提出了一種加入氣溫影響因子的隱馬爾科夫軌跡預測算法來完成鳥類遷徙運動過程中的時空軌跡預測。喻鋼［3］提出了一種雙向長短時記憶（Long Short-Term Memory，LSTM）和殘差網絡為主要結果的時空軌跡模型（Spatio-Temproal Trajectory Mod?el，STTM）有效根據出租車軌跡預測行程時間。鄧佳［4］提出了一種基于HMM模型的軌跡聚類方法（HMM-Cluster），有效地聚合相似性軌跡，發現交通量過載情況。

傳統的軌跡研究中，人們往往關注軌跡點在空間維度上的分布，沒有對軌跡的時態數據進行處理，但空間和時間屬性是軌跡點的基本特征，是反映軌跡狀態和演變過程的重要組成部分。時空軌跡相似度計算方法有很多，在不同環境下，有各自適合的算法。本文涉及的軌跡數據是采樣不均勻的，意味著兩條軌跡之間的軌跡點不在時間上一一對應。針對這種情況，本文在多子空間對應相似的聚類算法中的LCSS算法的基礎上，提出了LCSS+算法，改進了LCSS算法對于軌跡點比較時出現對時間閾值選取的敏感問題，由于單機在處理大數據集的局限，本文設計了分布式的LCSS+算法，進一步提升了聚類的速度，提升了系統的性能。

2 時空軌跡聚類方法介紹

兩個對象之間的相似度是這兩個對象相似程度的數值度量，相異度則是兩個對象差異程度的數值度量，距離通常視作相異度的方面［5］兩個對象相似度越高，相似度越高，相異度就越低，距離越小。依照相似度量所涉及的不同時間區間，可以將現有的時空軌跡聚類算法分為六類。主要有：1）時間全區間相似，代表的聚類方法有歐式距離［6］。2）全區間變換對應相似，代表算法有DTW［7］。3）多子區間對應相似，代表算法主要有最長公共子序列、編輯距離［8］。4）單子區間對應相似，代表算法主要有子聚類算法、時間聚焦聚類、移動微聚類、移動聚類。5）單點對應相似，代表算法主要有歷史最近距離、Fréchet距離。6）無時間區間對應相似，代表算法主要單向距離、特征提取方法。現主要介紹三種常用的算法。

2.1 基于歐式距離的相似度算法

在1993年，AGRAWAL R等就提出了基于歐式距離的軌跡間相似度的標識方法［9］。該方法要求計算的兩條軌跡的采樣點是一一對應的。即采用間隔相同、采樣點數（即軌跡長度）一致。軌跡間的距離由軌跡上對應各點間的距離通過求和或取最大/最小值得到。設P= 和Q= ，P、Q分別表示兩條軌跡的空間域離散采樣，該方法要求m=n，并且P和Q的每個采樣點一一對應，對應點的距離為

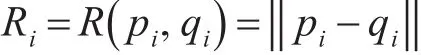
則軌跡之間的距離可以表示為

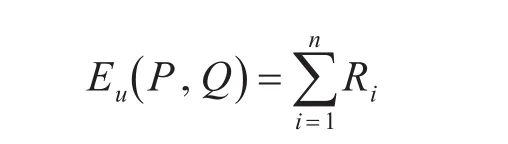
之后的研究對于該算法的效率方面記性了改進，利用數字信號處理的相關知識，提出利用離散傅里葉變換［10］、離散小波變換［11］、APCA［12］等方法提高運算效率。但這些方法與其基礎方法一樣。都對估計的采樣率與采樣點有嚴格的要求，在這種距離度量的算法之下，造成估計間的差異因素只能是噪聲，因此該方法也存在這對噪聲敏感等缺點。

2.2 基于Fréchet距離的相似度算法

在連續Fréchet距離的基礎上，Eiter和 Mannila提出了離散Fréchet距離的定義。

上式這個組合成為鏈A和B的Fréchet排列。

離散Fréchet距離不足以判別曲線的相似度，因為它表示的是曲線之間關鍵特征點的距離，故引入定義2。

2.3 基于編輯距離的相似度算法

編輯距離是一種源于文本處理的概念，它指的是將一個文本序列通過增、刪、改三種操作變成另外一個序列所需的最小操作數［13］。CHEN L等在編輯距離的基礎上進行了改進，提出了ERP［14］、EDR［15］。還有另外一種運用動態規劃的編輯距離，最長公共子序列距離（LCSS）。其目標是找出無需任何操作即相似的最長軌跡片段。給定兩個序列X和Y，如果Z既是X的一個子序列又是Y的一個子序列。例如，如果X=（A，B，C，B，D，A，B），Y=（B，D，C，A，B，A），則序列（B，C，A）即為X和Y的一個公共子序列。但是序列（B，C，A）不是X和Y的最長的公共子序列，因為它的長度等于3，而同為X和Y的公共子序列（B，C，B，A）其長度為4，所以序列（B，C，B，A）是X和Y的一個LCSS，序列（B，D，A，B）也是，因為沒有長度為5或者更大的公共子序列。求解最長公共子序列也是一個動態規劃的問題，假設有兩條長度分別為n和m的時間序列數據A和B，那么最長公共子序列的長度為［16］

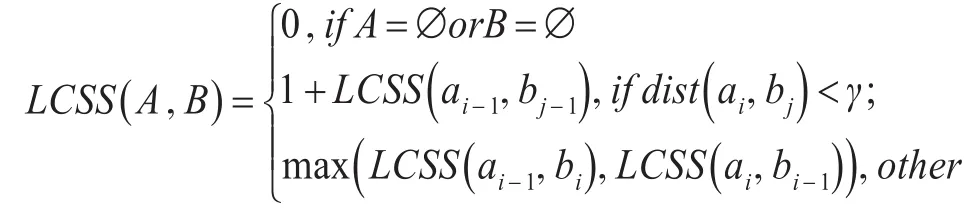
其中，γ是成員相似度量標準，i，j分別代表序列A和序列B的點下標。基于公共子序列的相似度公式可以定義為

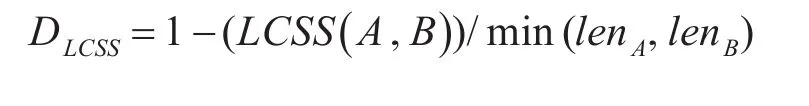
3 時空軌跡相似度計算

3.1 時空軌跡定義

由于時空軌跡的特殊性，以及后續算法的描述，現定義時空軌跡運算的所需要的基本定義。

定義3：時空軌跡中的軌跡點由可三元屬性構成，分別是時間，經度，緯度，時空軌跡中的第i個時空軌跡點記為：Pi=(ti，logi，lati)，ti代表軌跡中第i個軌跡點所處時間，logi代表第i個軌跡點的經度，lati代表第i個軌跡點的緯度。

定義7：時空軌跡Ta的時間序列tsa和時空軌跡Tb的時間序列tsb之間的交集定義為tsa∩tsb={P(ti)|MaxTa≥t≥MinTa∩MaxTb≥t≥MinTb}。

定義8：時空軌跡Ta和時空軌跡Tb之間的交集定義為Ta∩ Tb={Pi|Pi?Ta||Pi∈ Tb，Pi(t)∈(tsa∩ tsb)}

定義9：若時空軌跡Ta的最小時間MinTa和最大時間MaxTa與時空軌跡Tb的最小時間MinTb和最大時間 MaxTb滿足MinTb≤MinTa≤MaxTa≤MaxTb，則有 Ta∈tTb。

3.2 時空軌跡求交

在比較時空軌跡時，由于人員軌跡活動時間是不一致的，對于人員a的軌跡Ta和人員b的軌跡Tb，它們兩個在時空中，會表現出三種情形：

情形一：軌跡Ta和軌跡Tb在時間上不相交；

情形二：軌跡Ta和軌跡Tb在時間上部分相交；

情形三：軌跡Ta在時間上包含軌跡Tb或者軌跡Tb在時間上包含軌跡Tb。

對于情形一，由于兩條時空軌跡在時間上錯過，相似度為0。

3.3 時空軌跡相似度量標準

對時空軌跡進行求交運算后，就需要來計算兩條時空軌跡之間的相似度了，由于GPS定位會由于大氣層、人為干擾因素的影響，GPS定位會出現定位誤差，所以在比較兩條軌跡上的軌跡點時需要設置一個容錯閾值，軌跡Ta上軌跡點Pai和軌跡Tb上的軌跡點Pbj，經緯度轉換為距離的公式為

則認為這兩個軌跡點在空間上是一對空間相似點。由于要在時空軌跡點還有時間屬性，那么兩個軌跡點的相似度計算規則，可以定義如下：如果兩個軌跡點在空間上都不相似，那么兩個軌跡點就不是相似的。如果兩個軌跡點在空間上相似，兩個軌跡點時間上越接近，那么這兩個軌跡點越相似，否則就越不相似。則兩個軌跡點Pai、Pbj的相似值可以設為跡點Pai和軌跡點Pbj在時間上差距小于t時，軌跡點之間的相似性為1，而當軌跡點在時間上差距大于t時，軌跡點相似度會向0靠近，符合現實情況。

3.4 改進的LCSS算法LCSS+

對于時空軌跡來說，計算其最長公共子序列并轉換為LCSS距離可以衡量軌跡之間的相似度。LCSS的計算一般通過計算狀態轉移矩陣獲取。設LCSS（Tai，Tbj）為軌跡Tai和軌跡Tbj的之間的LCSS長度。Tai表示軌跡Ta上從位置編號0到i的軌跡點集合，同理Tbj，當 i=0 或者 j=0 時，LCSS（Tai，計算相似度時，對于軌跡點之間差距大于σ，認為其不是一個相似點，那么對于時間差值的閾值的選取非常敏感的。σ取值過大，會導致原本不相似的軌跡點變成相似點。為了方便計算，本文將每一天的時間進行劃分，10min為一個時間段。例如如果時間是9點整，那么所處時間段為9*60/10=54。即9點整是處于第54個時間段。當時空軌跡中一個時間段內的軌跡點有多個的時候，則計算多個軌跡點的平均位置，即個軌跡點的平均出現時間為為時間段內的軌跡點的數目。經過時間分段后，每個時間段內只有一個平均后的軌跡點，軌跡點的屬性包括時間、經、度、緯度，成了軌跡點序列。針對LCSS對軌跡點比較的時候，出現對時間差值的閾值選取的敏感性，本文提出了一種新的類似于LCSS的動態規劃算法，暫命名為LCSS+。上文提到，兩個時空軌跡點在空間上類似的時候，軌跡點之間的相似性為。在比較兩條軌跡的時候，目標是使軌跡點相似性之和最大，LC?SS+算法主要的思想是以軌跡點相似性和最大為目標來進行計算的，可以發現LCSS+也是一個動態規劃的問題，求解動態規劃問題的關鍵在于求解狀態轉移方程。

定義dp［i］［j］為軌跡Ta從1到i-1編號組成子序列，軌跡Tb從1到j-1編號組成子序列，它們所包含的最大的相似性和。當軌跡Ta的軌跡點Pai和軌跡Tb的軌跡點Pbi滿足dis （Pai(lat)，

圖1 LCSS+算法狀態轉移矩陣求解過程

箭頭表示兩個空間軌跡在空間位置上類似的情況下，其累計相似性和的轉移情況，例如在B（9：32）和B（9：50）在空間位置上都是屬于B點，在時間上想差19min，那么它的累計最優相似性和就是：之間的最大值，可以算出最大值為1.22，又在B（9：40）和B（10：02）在空間置上屬于B點，時間上想差為22分鐘，那么從dp[]2[3]轉移過來的累計最大相似性和為：1/（1+2.2*2.2）+1.22=1.39。而從dp［3］［3］轉移過來的累計最大相似性和為1.45。顯然更大，故dp［3］［4］的取值應為1.45。因為從時間上來看，雖然如果兩個軌跡在行進過程中在B點可以取兩個公共B，但是位于兩個公共B的軌跡點時間差比較大，還不如一個公共B，即B（（9：40）和B（9：51）點所帶來的相似性累計。

對應的LCSS算法在求解過程中的狀態轉移矩陣如圖2。

如上圖所示LCSS算法在求解狀態矩陣的時候，只有兩個公共相似點，第一對相似點為A（9：25）和 A（9：30），第二對相似點為 D（10：13）和 D（10：15）。最終求解出來的最大相似性和為2，相比于LCSS+算法其因選取時間間隔敏感的問題就凸顯出來，當選取10min作為間隔點的時候，LCSS算法會損失一些可能相似的公共點，比如B（9：40）和B（9：51），就因為相差11min就舍去公共點，而造成了一定的誤差。

3.5 分布式LCSS+算法設計

由于人員軌跡數據量很大，某地區一天產生的人員軌跡就有970萬條，若放在單機上運行，速度會比較慢，而且當一次比較的軌跡數量過多，會引起內存溢出的異常。這對指定人員的軌跡尋找與其潛在的相似軌跡，需要進行大量的計算。故本文使用了MapReduce編程模型，實現了LCSS+算法。MapReduce是在Hadoop架構里面的并行處理框架，提供了高層次的API，易于編程，對大量數據處理有很好的優勢。下面描述一下主要的MR算法處理流程。1）人員軌跡的軌跡點實質上是一個4維向量（身份ID，經度，緯度，時間），將指定的人員軌跡Ta序列化存儲在集群中。2）需要將一天的軌跡點規約到每一個人身上，形成完整的軌跡。3）之后要做的就是軌跡時間求交，到一個共同的時間范圍內進行LCSS+算法計算出每條軌跡與Ta之間的軌跡相似性。4）選取軌跡比較中軌跡相似度比較大的n條軌跡作為輸出。經過設計，這個過程需要兩個有依賴關系的MapReduce即可完成。下面給出計算的偽代碼。

Reduce階段的偽代碼與Map階段類似，故不再復述。經過上述兩個依賴的MapReduce任務就可以輸出最大的k個軌跡相似度值的人員。

4 系統效果評估

4.1 實驗環境

實驗采用的集群環境由5臺內存為DDR4 16GB*4的I620-G20服務器組成，機器均運行red?hat操作系統，裝有2.60版本的Hadoop集群環境。

首先在單機環境下，比較LCSS算法和本文的LCSS+算法在比較人員相似性的準確率。南京某地區，實驗人員A以及和A一起同行的人員有50人，向軌跡數據集中加入其他不相關人員9000條數據，設置比較軌跡點時空間距離的閾值為1km，選取不同的時間閾值后，LCSS算法和LCSS+算法對相同數據集的表現結果如圖3。

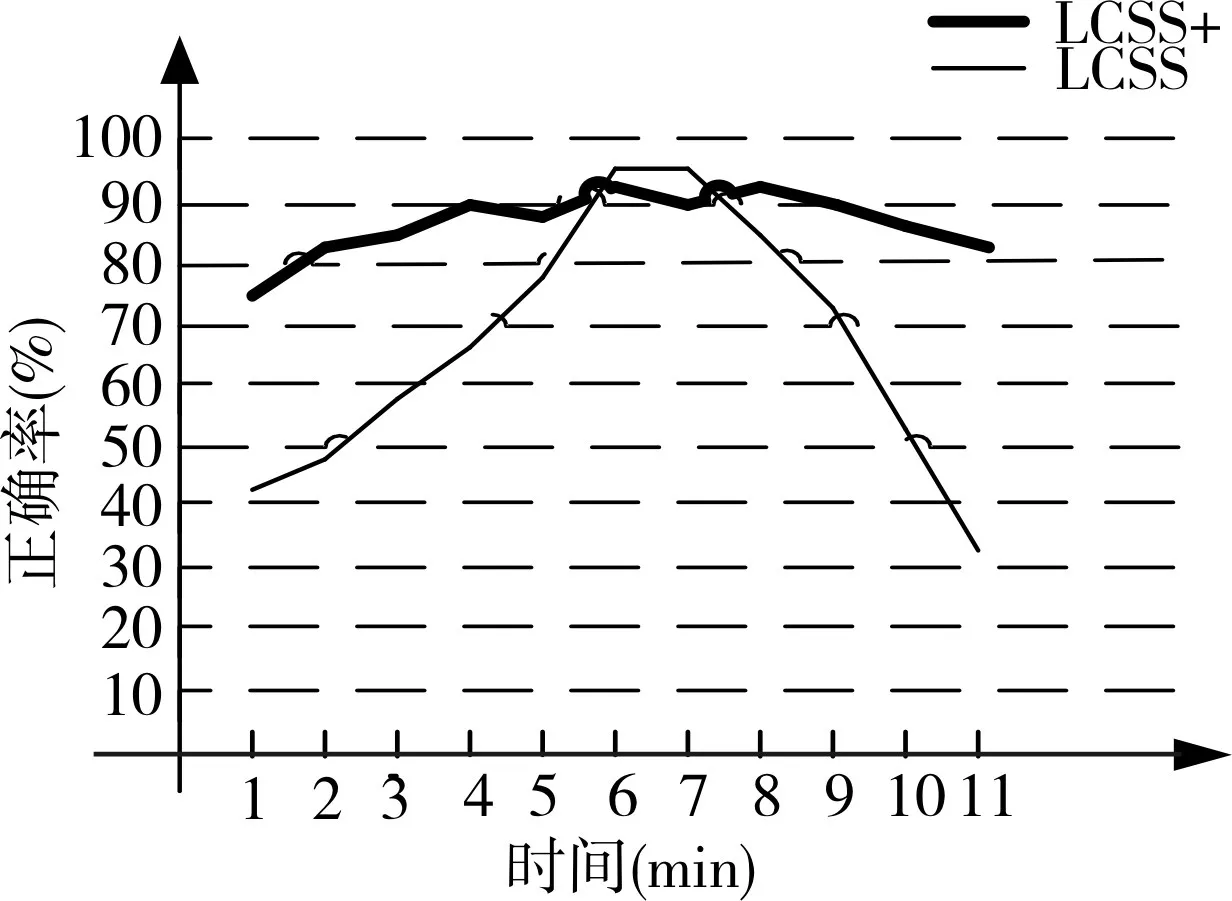
圖3 LCSS與LCSS+算法對比

正確率的評價標準是，選取的相似度最高的50條數據，看有多少人是原本在實驗人員A同行人員。可以看出LCSS算法是一個拋物線形的曲線，在5.5min～7.5min內正確率略高于LCSS+算法，但是在 1min～5.5min和7.5min～11min內正確率卻低于LCSS+算法，說明了LCSS算法對于時間閾值的選取非常敏感，而LCSS+算法對于時間閾值的選取表現平穩，在平均情況下優于LCSS算法。

4.2 分布式LCSS+和LCSS+算法對比

在單機環境下和Hadoop集群上分別運行LC?SS+算法，逐步增大數據量，查看運行時間對比。實驗結果如圖4。

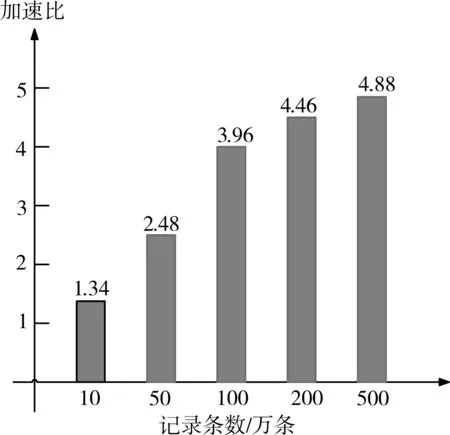
圖4 分布式LCSS+與LCSS運行加速比

加速比為Hadoop集群上運行時間除以單機環境下的運行時間的結果。從圖4可以看出，當逐步增大數據量時，加速比越來越大，逐漸趨向于5，說明分布式LCSS+算法的運行效率大數據集的情況下要遠優于單機下的LCSS+算法。

5 結語

本文對時空軌跡數據進行離散化處理，分析傳統了時空軌跡處理算法LCSS，發現它對于時間閾值取值范圍的敏感性，提出了一種平均情況下表現平穩的算法LCSS+，能夠對特定人員的伴隨軌跡進行有效的挖掘，有較高的執行效率。在LCSS+的基礎上，考慮到數據量大的問題，提出了分布式環境下的LCSS+算法，并通過實驗驗證了分布式LCSS+算法能夠提升算法在大數據的情況下的運行效率，為后續進一步研究時空軌跡數據挖掘提供了很好的參考依據，未來可以嘗試更多的相似度度量方法，并比較其在各種環境下的表現情況。