并發(fā)感知的業(yè)務(wù)過程事件序列編輯距離?

常 震 戴汪洋 宋 巍 李晅松

（南京理工大學(xué)計算機科學(xué)與工程學(xué)院 南京 210094）

1 引言

業(yè)務(wù)過程管理旨在加快制定，分析和改進業(yè)務(wù)過程的速度，而圍繞著過程所建立的組織，具有更高的敏捷性、效率和效益。為了支持管理決策，業(yè)務(wù)過程日志記錄了過程實例的執(zhí)行，通過分析業(yè)務(wù)過程日志數(shù)據(jù)可以了解業(yè)務(wù)過程的執(zhí)行，實現(xiàn)業(yè)務(wù)過程的管理、改進與再造［1～3］。在日志噪音修復(fù)、過程挖掘中的合規(guī)性檢驗方面，不可避免地要對日志中的事件序列進行差異性度量，如驗證事件序列的修復(fù)情況等［4～6］。

在計算機科學(xué)中，字符串編輯距離是重要而基本的概念，它在拼寫檢查與自動修復(fù)等方面有著廣泛的應(yīng)用［7～8］。雖然可以使用字符串編輯距離來定義業(yè)務(wù)過程日志中事件序列間的編輯距離，但該方法在應(yīng)用于含并發(fā)的業(yè)務(wù)過程時并不理想。例如在日志修復(fù)時，一個含有噪音的事件序列可能存在多個不同的正確修復(fù)方案［4～6］，不同修復(fù)方案的差異往往僅體現(xiàn)在存在并發(fā)關(guān)系的事件的先后順序上。如果利用字符串編輯距離作為評判依據(jù)，這些正確的修復(fù)有很多不被認(rèn)為是最優(yōu)修復(fù)。

考慮到現(xiàn)有方法的不足，本文針對業(yè)務(wù)過程的并發(fā)性以及事件序列可能產(chǎn)生的噪音類型，給出了業(yè)務(wù)過程事件序列編輯距離的全新定義，提出了相應(yīng)的求解算法，并將該算法實現(xiàn)為一個圖形化的桌面工具“BPETED”（Business Process Event-trace Ed?it Distance）。該工具可以解析XES格式的事件日志文件，并計算指定的事件序列間編輯距離，同時給出時間消耗。本文通過IBM公司一個真實的業(yè)務(wù)過程日志對算法進行分析，驗證算法的有效性和高效率。

2 背景知識

2.1 業(yè)務(wù)過程

Petri網(wǎng)［9］是一種簡潔通用的表示業(yè)務(wù)過程的建模語言，并且擁有一套完善的數(shù)學(xué)理論進行過程分析。因此，其他如BPEL、BPMN、EPC等工業(yè)建模語言也經(jīng)常被轉(zhuǎn)化為Petri網(wǎng)進行高級的分析與應(yīng)用［10～11］。本文延用慣例，也使用 Petri網(wǎng)來表示業(yè)務(wù)過程。

定義1（Petri網(wǎng)）Petri網(wǎng)是一個滿足如下條件的三元組PN=(P，T，F(xiàn))：

·P是庫所的有限集合；

·T是變遷的有限集合，并且滿足P∩T=Φ；

·F?(P×T)∪(T×P)是被稱為流關(guān)系的有向弧的有限集。

Petri網(wǎng)所表示的業(yè)務(wù)過程中的起始庫所和終止庫所只有一個，并且它是可以執(zhí)行的。業(yè)務(wù)過程每執(zhí)行一次便產(chǎn)生一條過程實例，該過程實例可以用一條事件序列σ={t1，t2，t3，...，tn} 來表示，其中t1，...，tn代表事件，這n個事件按照發(fā)生的先后順序進行排列。將這些過程實例記錄下來便形成了事件日志。

定義2（事件序列與事件日志）給定一個業(yè)務(wù)過程W=(P，T，F(xiàn))，其初始狀態(tài)為M0，事件序列σ∈T*是從狀態(tài)M0轉(zhuǎn)化為狀態(tài)M的一條活動序列，其中M為W的任意一個可達(dá)的狀態(tài)。事件日志為事件序列的集合，即L={σ|σ∈T*}。

圖1展示了一個含并發(fā)的業(yè)務(wù)過程Petri網(wǎng)模型。

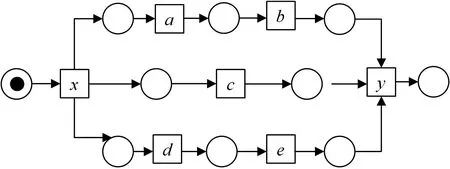
圖1 含并發(fā)的Petri網(wǎng)

2.2 字符串編輯距離

關(guān)于編輯距離問題的研究可以追溯到字符串間編輯距離，這個概念最早由俄國科學(xué)家Levensh?tein于1965年提出，因此，編輯距離也被稱為“Lev?enshtein distance”（以下簡稱 L 氏距離）［15～16］。編輯距離是一種通過計算將一個字符串轉(zhuǎn)換為另一個字符串所需的最小操作次數(shù)來量化兩個字符串間相似性的方式［7～8］。它在自然語言處理、生物信息科學(xué)以及計算機科學(xué)等方面有著廣泛的應(yīng)用。

字符串間編輯距離計算利用動態(tài)規(guī)劃的算法思想，將兩個字符串間的編輯距離轉(zhuǎn)換為子序列間的編輯距離，用一個維度大小分別為源字符串長度和目標(biāo)字符串長度的矩陣來保存計算過程中求得的子序列編輯距離［12～14］。一般來說，兩個字符串的編輯距離越短，則表示它們越相似，如果兩個字符串相同，則它們的編輯距離為零。

到目前為止，對編輯距離的定義有很多擴展，不同的編輯距離定義了不同的字符串操作集合。其中，L氏距離的操作集合包括刪除、插入、替換［15～16］。此外還存在最長公共子序列（LCS）距離，操作集合只包含刪除、插入兩類操作；海明距離（Hamming distance），只允許替換操作等多種擴展類型的編輯距離［7］。除此之外，有人還提出了一些其他的基本操作，如鍵入文字時常見的錯誤，交換相鄰兩個字符的順序。由于以上各種編輯距離定義不能直接應(yīng)用于含并發(fā)的業(yè)務(wù)過程事件序列，因此，在章節(jié)3.2中我們給出了業(yè)務(wù)過程事件序列編輯距離的全新定義。

3 編輯距離算法

3.1 事件間關(guān)系

由于字符串中的字符間的關(guān)系是相互獨立的，因此在計算字符串編輯距離的過程中，不考慮字符間的相互關(guān)系。但對于事件序列來說，事件間存在一系列關(guān)系，這些關(guān)系可能會對事件序列編輯距離產(chǎn)生影響。

事件序列間的關(guān)系包括直接先于關(guān)系（符號表示為>）與并發(fā)關(guān)系（符號表示為||）等。直接先于關(guān)系與并發(fā)關(guān)系的定義同文獻［17］中定義相同。

定義3（事件間關(guān)系）給定一個業(yè)務(wù)過程W=(P，T，F(xiàn))的事件日志L，存在事件a，b，滿足a，b∈T，a≠b，則a，b存在以下關(guān)系：

·a>b，對于任一事件序列σ={t1，t2，t3，…，tn}，當(dāng)a=ti，b=t(i+1)，則a>b；

·a||b，當(dāng)且僅當(dāng)a>b，并且b>a時，a||b。

算法1旨在挖掘業(yè)務(wù)過程事件日志中事件間的并發(fā)關(guān)系集合。第1行對集合進行初始化；第2～4行挖掘事件間的直接先于關(guān)系集合；第5～8行根據(jù)之前獲得的事件間直接先于關(guān)系集合，挖掘事件間的并發(fā)關(guān)系集合，其中第5～6行利用二重循環(huán)遍歷事件日志中所有的事件對，第7～8行根據(jù)事件間直接先于關(guān)系判斷事件間是否存在并發(fā)關(guān)系；第9行，返回事件間的并發(fā)關(guān)系集合。該算法的時間復(fù)雜度為Θ(N*l+|T|2)，其中N*l為挖掘直接先于關(guān)系集合的時間復(fù)雜度，|T|2為挖掘并發(fā)關(guān)系集合的時間復(fù)雜度，N表示事件日志中事件序列的數(shù)量，l表示事件日志中事件序列的平均長度， ||T表示事件日志中事件的數(shù)量。

3.2 編輯距離

字符串編輯距離算法的計算不需要考慮字符間的并發(fā)關(guān)系，但對于事件序列編輯距離來說，事件間的并發(fā)關(guān)系可能會對編輯距離產(chǎn)生影響。本節(jié)針對業(yè)務(wù)過程的并發(fā)性以及事件序列中可能產(chǎn)生的噪音類型，對業(yè)務(wù)過程事件序列編輯距離進行了全新定義。

現(xiàn)實世界中的事件日志中存在三類可能的噪音類型：缺失、冗余、亂序［4～6］，針對這三類噪音類型，我們分別定義了三類業(yè)務(wù)過程事件序列基本編輯操作：刪除、插入、交換。

定義4（基本編輯操作）事件序列間的基本編輯操作包括刪除、插入、交換：

·刪除：刪除事件序列中任意一個事件，如刪除事件序列abc中的事件b后，事件序列變?yōu)閍c；

·插入：在事件序列中任意位置插入一個已定義或未定義的事件，如對于事件序列ab，在事件b之后插入一個未定義的事件c，事件序列變?yōu)閍bc；

·交換：交換事件序列中任意兩個相鄰且非并發(fā)的事件，如對于事件序列abcd，事件b，c為非并發(fā)關(guān)系，交換事件b，c，事件序列變?yōu)閍cbd。

特別地，交換兩個相鄰且并發(fā)的事件對編輯距離不產(chǎn)生影響。

定義5（編輯距離）給定兩個事件序列σ與δ，σ與δ間的編輯距離D(σ，δ)是將其中一條事件序列轉(zhuǎn)化為另一條事件序列所需的最少基本編輯操作次數(shù)。

3.3 編輯距離計算

本節(jié)提出了編輯距離的求解算法，該算法的創(chuàng)新點在于能夠消除事件間并發(fā)關(guān)系對事件序列編輯距離產(chǎn)生的影響，準(zhǔn)確度量事件序列間的差異。

我們運用動態(tài)規(guī)劃的思想，用矩陣Dm×n來存儲計算過程中子序列間的編輯距離。假設(shè)待求的兩條事件序列分別為 σ1={t1，t2，t3，…，tm}和 σ2={t1，t2，t3，…，tn}，則矩陣值 D[i][j]（其中 i≤m，j≤n）表示事件序列σ1的子序列σ'1={t1，t2，t3，...，ti} 和事件序列 σ2的子序列={t1，t2，t3，...，tj} 間的編輯距離。矩陣 Dm×n的維度分別為 |σ1|+1 和 |σ2|+1 ，其中 ||σ1表示事件序列σ1的長度， ||σ2表示事件序列σ2的長度。矩陣值 D[|σ1|][|σ2|]即為事件序列 σ1與σ2間的編輯距離。

算法的求解過程為首先對矩陣D的第零行與第零列進行初始化，將第零行中的每個值賦值為對應(yīng)的列號，將第零列中的每個值賦值為對應(yīng)的行號；然后計算矩陣D中的其他值，計算過程需要考慮三類情況，其中情況1、2與字符串編輯距離中考慮的情況相同［7～8］，情況3考慮了并發(fā)事件對編輯距離的影響，為本文的創(chuàng)新點。這三類情況分別如下。

1）矩陣值D[i][j]等于與其鄰接的上方與左方矩陣值中的最小值加1，用式（1）表示為

D[i][j]=min(D[i][j-1]，D[i-1][j])+1 （1）

2）當(dāng)指針i指向的事件序列σ1中的事件σ1[i]與指針 j指向的事件序列σ2中的事件σ2[j]相同時，矩陣值D[i][j]等于矩陣值D[i-1][j-1]，用式（2）表示為

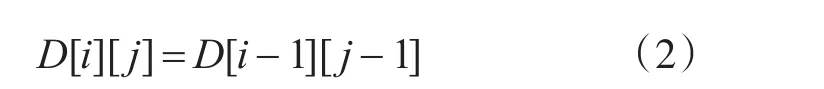
首先，對于矩陣值D[l-1][k-1]，雖然我們不可以直接得出該值，但卻可以通過矩陣值D[i-1][j-1]間接計算求得。在事件序列中將事件tl移至事件ti之前且相鄰的位置后，事件序列={t1，t2，...，t(l-1)，tl} 與 σ2'2={t1，t2，t3，...，t(j-1)} 間 的編輯距離將發(fā)生改變，產(chǎn)生的影響可以用式（3）表示為

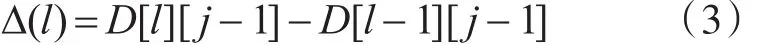
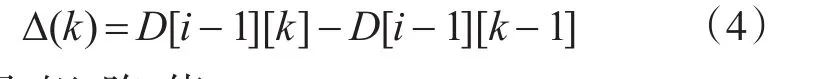
可得矩陣值 D[l-1][k-1]=D[i-1][j-1]-?(l)-?(k)。

其次，將事件tl移至事件ti之前且相鄰的過程中，當(dāng)發(fā)生交換的事件與事件tl為非并發(fā)關(guān)系，且該事件在事件 序列={t1，t2，t3，...，t(j-1)} 中出現(xiàn)時，會使編輯距離加1，用符號lnum表示滿足條件的事件的數(shù)量。類似的，用符號knum表示將事件tk移至事件tj之前且相鄰的過程中滿足類似條件的事件數(shù)量。

最后，還需要判斷事件ti與tj間的關(guān)系，若為非并發(fā)關(guān)系，則編輯距離加1，否則編輯距離不變。用式（5）表示情況3下的矩陣值為

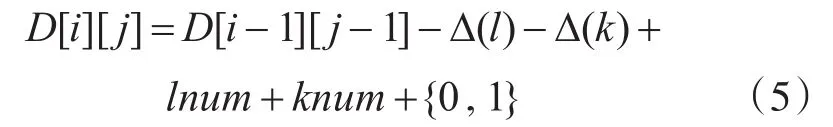
取上述三類情況中求得的式（1）、（2）、（5）中的最小值為矩陣值D[i][j]的最終值。

算法2設(shè)計用來計算含并發(fā)的業(yè)務(wù)過程事件序列編輯距離。第 1 行，創(chuàng)建一個矩陣 D(|σ1|+1)×(|σ2|+1)來存儲算法計算過程中的中間值；第2～3行，使用二重循環(huán)對矩陣D中的值逐個進行求解；第4～5行，對第零行與第零列進行初始化；第6行，計算情況1下的矩陣值D[i][j]；第7～8行，計算情況2下的矩陣值D[i][j]；第9～20行考慮了情況3；第10行計算式（3）和式（4）；第11行對lnum，knum和s進行初始化；第12～14行對lnum進行計算，第15～17行對knum進行計算；第18～19行判斷事件ti與tj之間的關(guān)系，若為并發(fā)關(guān)系，則將s置為0；第20行計算式（5）；第21行返回待求事件序列編輯距離。該算法的時間復(fù)雜度為 Θ(|σ1|×|σ2)，其中 ||σ1表示事件序列σ1的長度， ||σ2表示事件序列σ2的長度。

4 評估

4.1 工具實現(xiàn)

為了評估本文算法的有效性與高效率，同時方便相關(guān)領(lǐng)域內(nèi)其他研究人員使用，我們在Eclipse集成環(huán)境中使用Java語言開發(fā)了原型工具“BPET?ED”，該工具運行在裝有JDK1.8的機器上，其使用分為以下三個步驟：

1）日志解析：如圖2所示，在“日志”顯示面板下，點擊“選擇xes日志文件”按鈕，選擇好日志文件之后點擊“解析日志文件”按鈕，可在下方顯示框內(nèi)顯示事件日志中每條事件序列的起始事件、終止事件、長度與數(shù)量等信息，并在“計算編輯距離”按鈕下方顯示挖掘事件間關(guān)系消耗的時間。點擊“顯示事件序列”按鈕可以查看事件序列詳情。

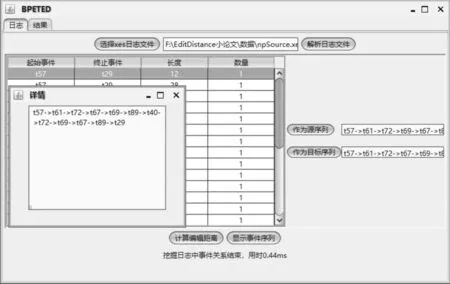
圖2 原型工具

2）編輯距離計算：選中顯示框中的事件序列，點擊“作為源序列”按鈕可以將該事件序列作為源序列，或者直接在編輯框內(nèi)編輯；同樣地，選擇目標(biāo)序列或直接編輯。點擊“計算編輯距離”按鈕，計算源序列和目標(biāo)序列間的編輯距離，并在“計算編輯距離”按鈕下方顯示計算編輯距離消耗的時間。

3）結(jié)果展示：如圖3所示，計算完編輯距離后，在“結(jié)果”顯示面板下，點擊“顯示結(jié)果”按鈕可以以表格形式查看矩陣的值，矩陣中最右下角的矩陣值即為待求的事件序列編輯距離。

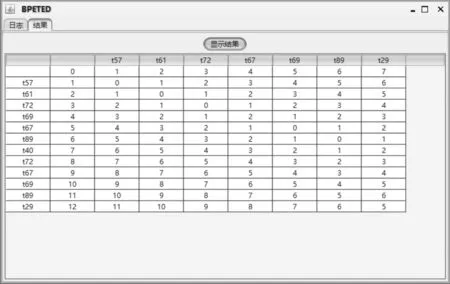
圖3 含循環(huán)業(yè)務(wù)過程的事件序列編輯距離計算結(jié)果

4.2 案例分析

圖4為一個帶循環(huán)且含并發(fā)的業(yè)務(wù)過程案例，該案例來源于IBM公司一個真實的業(yè)務(wù)過程。由于該業(yè)務(wù)過程較大，影響在本文中的呈現(xiàn)效果，因此我們對案例進行了一定程度的簡化。

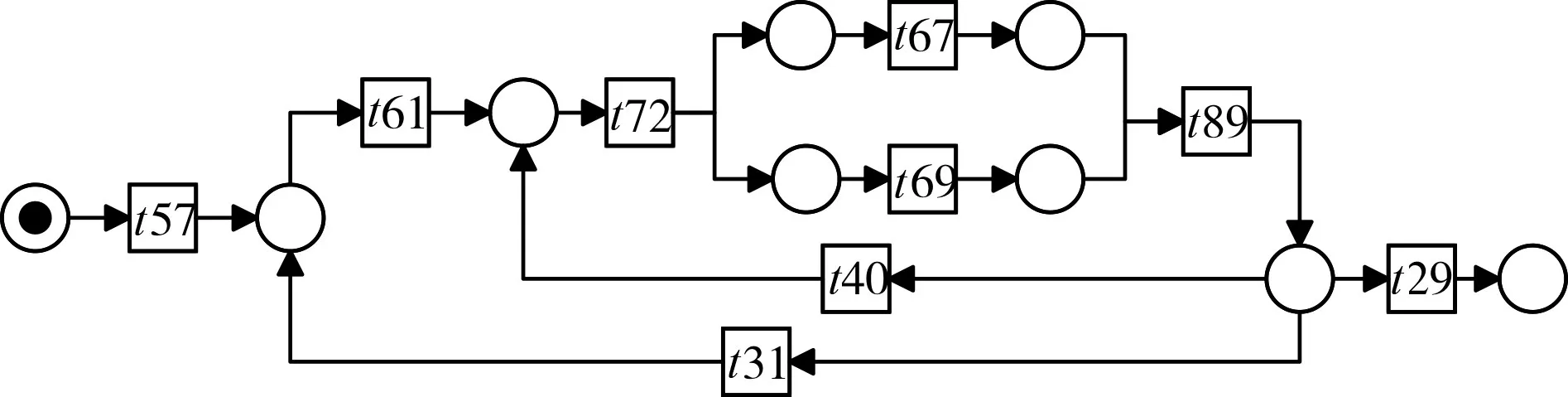
圖4 帶循環(huán)且含并發(fā)的Petri網(wǎng)

該業(yè)務(wù)過程存在兩條并發(fā)支路并包含兩個循環(huán)節(jié)點t40 與t31 。事件序列σ1={t57，t61，t72，t69，t67，t89，t40，t72，t67，t69，t89，t29} 與事件序列σ2={t57，t61，t72，t67，t69，t89，t29}為該業(yè)務(wù)過程產(chǎn)生的兩條運行實例。以這兩條事件序列為例，對編輯距離計算過程進行分析。

首先按照算法1挖掘出事件間的關(guān)系集合，其中事件間并發(fā)關(guān)系集合為||={t67||t69}；然后按照算法2，創(chuàng)建矩陣D12×7，其中l(wèi)2為事件序列σ1的長度，7為事件序列σ2的長度。對矩陣進行初始化之后逐個求解矩陣中剩余的值。舉例說明算法2的求解過程。

對于矩陣值D[1][1]，根據(jù)式（1）計算情況1的值 為D[1][1]=min(D[0][1]，D[1][0])+1=2 ；由 于σ1[1]=σ2[1]，滿足情況 2的條件，按式（2）計算得D[1][1]=min(D[0][0]，D[1][1])=0 ；因為當(dāng)前不存在位置相互交換事件，所以不需要考慮情況3，最終得D[1][1]=0。

對于矩陣值D[1][2]，根據(jù)式（1）計算得，D[1][2]=min(D[0][2]，D[1][1])+1=1，當(dāng)前不滿足其他情況的條件，得D[1][2]=1。

對于矩陣值D[5][5]，指針i，k指向事件e，指針j，l指向事件 c，l=4，i=5，k=4，j=5。計算式（1）得D[5][5]=min(D[4][5]，D[5][4])+1=2 ；不滿足σ1[5]=σ2[5]，不考慮情況2；由于當(dāng)前存在位置相互交換的事件，計算式（3）得 ?(l)=D[l][j-1]-D[l-1][j-1]=1；計算式（4）得 ?(k)=D[i-1][k]-D[i-1][k-1]=1；在事件序列σ1中，事件t69與t67之間無其他事件，得lnum=0；在事件序列σ2中，事件t67與t69之間沒有其他事件，得knum=0；事件t67與t69為并發(fā)關(guān)系，不對編輯距離產(chǎn)生影響，計算式（5），得D[5][5]=D[i-1][j-1]-?(l)-?(k)+lnum+knum+{0，1}=0；取式（5）與式（1）的最小值0為D[5][5]的最終值。

對于矩陣值D[9][5]，指針i，k指向事件c，指針j，l指向事件 s，l=4，i=9，k=4，j=5。計算式（1），得D[9][5]=min(D[9][4]+1，D[8][5]+1)=4 ；由于不滿足σ1[9]=σ2[5]，無需計算式（2）；計算式（3）得 ?(l)=D[l][j-1]-D[l-1][j-1]=1；計算式（4）得 ?(k)=D[i-1][k]-D[i-1][k-1]=-1；在事件序列σ1中，事件t69與t67之間存在事件t67，t89，t40，t72，其中事件t72與t69為非并發(fā)關(guān)系，且t72在事件序列={t57，t61，t72}中出現(xiàn)過，得lnum=1；在事件序列σ2中，事件t67與t69之間不存在事件，得knum=0；事件t67與t69為并發(fā)關(guān)系，對編輯距離不產(chǎn)生影響，計算式（5）得 D[9][5]=D[i-1][j-1]-?(l)-?(k)+lnum+knum+{0，1}=5；取式（1）與式（5）的最小值4為D[9][5]的最終值。

矩陣計算完成后可得圖3，求得事件序列σ1與σ2間的編輯距離D[12][7]=5，該值恰好等于業(yè)務(wù)過程中循環(huán)部分的事件序列長度，表明計算結(jié)果正確。

我們將該實例運行在Inter（R）3.60GHz處理器，16GB內(nèi)存的Windows8.1系統(tǒng)的臺式機上。經(jīng)過100次計算，統(tǒng)計得到平均事件關(guān)系挖掘時間為0.62ms，平均事件序列編輯距離計算時間為0.49ms，表現(xiàn)了算法具有很高的效率。

5 結(jié)語

本文針對業(yè)務(wù)過程的并發(fā)性以及事件日志中可能存在的三類噪音類型，定義了三類事件序列基本編輯操作，并給出了業(yè)務(wù)過程事件序列編輯距離的全新定義。基于該定義，在字符串編輯距離求解算法基礎(chǔ)上，提出了一種計算含并發(fā)的業(yè)務(wù)過程事件序列編輯距離的算法。該算法能夠有效處理含并發(fā)的業(yè)務(wù)過程，忽略由并發(fā)事件交換對編輯距離產(chǎn)生的影響。我們將該算法實現(xiàn)在“BPETED”工具中，并通過一個實際案例分析闡明了算法的有效性和高效率。