基于網絡分析儀的3D Transmon相干測量方法*

吳小宇 趙虎 李智 ?

1) (四川大學電子信息學院,成都 610065)

2) (航空工業西安飛行自動控制研究所,西安 710065)

3D Transmon是目前已知退相干時間較長的一種超導量子比特,在超導量子計算、量子光學、腔量子電動力學等方面具有重要的應用.拉比振蕩是表征量子系統退相干時間的重要方法,也是體現量子系統能夠進行能級演化的基本實驗.對3D Transmon進行拉比振蕩測試,需要進行嚴格的時序控制,測試調試的過程較為繁瑣.本文制備了3D Transmon樣品,對其基本參數進行了測試表征,創新性地提出了一種基于網絡分析儀的拉比振蕩測試方法,基于該方法的測試系統搭建簡單,可作為迅速驗證3D Transmon是否具備量子特性的一種手段,該方法也可推廣至其他量子系統進行時域特性的初步驗證.

1 引 言

基于約瑟夫森結的超導量子計算[1?4]由于能夠與經典微電子工藝兼容、退相干時間長、制備基態簡單、量子比特之間的耦合較為容易以及可規模化等優點,被認為是目前最有可能實現量子計算機的方案之一[5?8].國際上有許多團隊都致力于用超導的方式來實現量子計算機[9?14].超導量子計算的核心單元為超導量子比特,目前已實現的超導量子比特有 charge qubit[10],flux qubit[15],phase qubit[12],quantronium[16],Xmon[17],C-shunt flux qubit[18]等,除此之外,還有結合超導諧振腔實現的量子比特,包括基于共面波導諧振腔實現的量子比特[13],以及基于三維超導諧振腔實現的量子比特,即 3D Transmon[14].3D Transmon 中兩個電極板(pad)和微波腔一起構成并聯在Josephson結的大電容,用于壓制電荷噪音對量子比特相干性的影響.這種方法(即用大電容并聯在Josephson結來壓制電荷噪音對超導量子比特相干性的影響的方法)最早是由You 等[19]提出,對應的超導量子比特叫 capacitively shunted flux qubit (也叫C-shunt flux qubit),即“電容并聯磁通量子比特”.

本文通過雙角度蒸發[15]的方法在氧化硅襯底上制備了樣品,并將樣品放置在三維超導諧振腔中心處形成3D Transmon樣品.采用基于腔量子電動力學的色散讀出方法[20],對量子比特的基本性能進行了測試表征,用網絡分析儀、微波源以及任意波形發生器對3D Transmon進行了相干測量操作,當改變激勵微波信號的功率時,相干振蕩的頻率與微波信號的幅度呈現出較好的線性.對比數據采集卡Jaynes-Cummings[21]方法進行拉比振蕩的測試結果,可以看出網絡分析儀色散法得到的退相干時間小于數據采集卡Jaynes-Cummings得到的退相干時間,由于網絡分析儀色散測試法對于測量時序的要求較為簡單,測試系統搭建較為容易,可作為驗證樣品具備量子特性的一種方法補充.

2 3D Transmon 量子比特

Transmon[22]量子比特實際上是由 charge qubit演變而來,設 charge qubit的柵電容為Cg,柵電壓為Vg,約瑟夫森結的結電容為CJ,則柵電壓吸引的庫伯對數目ng=CgVg/2 e,庫伯盒的總充電能為 4EC=(2 e)2/2(CJ+Cg),則 charge qubit的哈密頓量可以寫為

其中EJ為庫伯盒的約瑟夫森能,n為庫伯對的數目,為粒子數算符.選取不同的EJ和EC,對(1)式進行求解,就可以得到不同EJ/EC下的能帶圖.當EJ/EC較小時,量子比特的能級隨ng變化較大;當EJ/EC較大時,量子比特的能級變得較為扁平,此時構成的量子比特為Transmon.

將Transmon與超導諧振腔耦合起來,可通過諧振腔的狀態對Transmon的狀態進行讀取,腔量子電動力學的JC哈密頓量為[7]

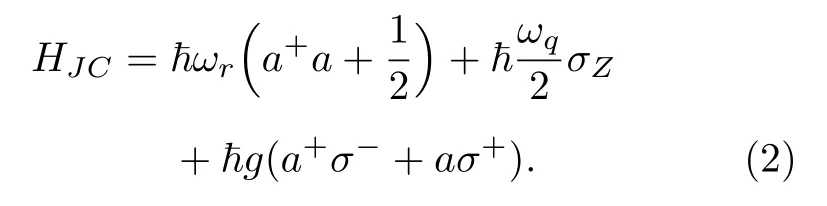
通過雙角度蒸發的方法得到的Transmon樣品的f01=9.2709 GHz,f12=9.0100 GHz,充電能EC=348.74 MHz,約瑟夫森能EJ=11.5560 GHz.將該Transmon放置在三維超導諧振腔[23]的第一模態處,得到 3D Transmon 樣品.三維超導諧振腔的第一模態頻率fC=8.108 GHz,有載品質因數為 4.8 × 105.對 3D Transmon 的S21參數進行變功率掃描得到如圖1所示的結果.

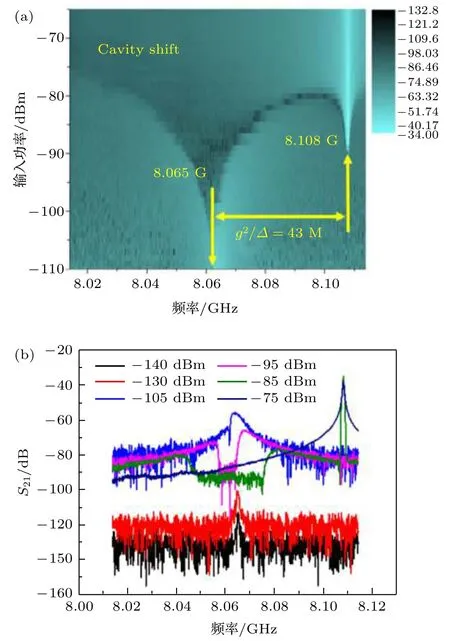
圖1 3D Transmon 的 S21變功率掃描結果 (a) S21強度圖;(b)部分 S21曲線Fig.1.The power change scan S21 of 3D Transmon: (a) Intensity graph of S21;(b) partial S21 curve.

從圖1可看出,當輸入功率逐漸下降時,諧振腔內的微波光子數逐漸下降,即量子比特與光子的相互作用對諧振腔的影響越來越明顯,諧振腔的第一模態頻率從 8.108 GHz 逐漸變到 8.065 GHz,這反映出諧振腔與量子比特的耦合g2/D=43 MHz.

3 色散法測量 3D Transmon

為了對3D Transmon進行測試,搭建了基于稀釋制冷機的超低溫測試系統,整個測試系統的搭建思路是輸入信號逐級衰減,輸出信號逐級放大,為了有更好的信噪比.如圖2所示,任意波形發生器與微波源通過一套混頻電路可提供脈沖長度可調的量子比特激勵信號,網絡分析儀通道1輸出信號,通道2接收信號,為了使不同的設備頻率基準完全相同,三臺設備都用同一個10 MHz的基準源.

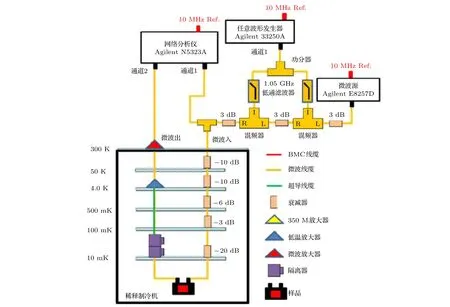
圖2 3D Transmon 測試系統Fig.2.3D Transmon measurement system.

3D Transmon安裝在稀釋制冷機的 10 mK溫區,輸入信號經過了 5 個衰減器,共計–49 dB 的衰減,輸出級有兩個隔離器,為了盡量少的將放大器以及輸出線路的噪聲引入樣品,提高整個測試系統的信噪比.輸出線路從10 mK到4 K之間采用超導微波線纜,輸出線路在4 K級進行一次放大,在室溫區進行了二次放大.

給量子比特施加f01=9.2709 GHz的連續微波激勵信號,微波功率為–110 dBm,網絡分析儀的掃描功率設定為–140 dBm,掃描S21參數,得到如圖3所示的結果.

從圖3可以看出,S21曲線上有兩個諧振峰,8.065與8.045 GHz分別代表量子比特處于和的兩個狀態,對8.065 GHz處的諧振峰幅度和相位進行測量,可判斷量子比特的狀態,這種量子比特的讀出方法為色散讀出法.

圖3 微波信號連續激勵量子比特時的 S21 曲線Fig.3.The S21 curve for the qubits excited by continuously microwave.

4 基于網絡分析儀的 3D Transmon相干測量

受限于目前的工藝以及測試系統等原因,目前制備的3D Transmon樣品的退相干時間普遍在1 μs的水平,因此激勵量子比特的周期選為 5 μs可以滿足量子比特激勵后充分冷卻到基態的要求.

網絡分析儀的采樣周期取決于中頻帶寬(IF Bandwidth),網絡分析儀 Agilent N5323 A 的中頻帶寬最大為 15 MHz,其對應采樣時間約為 67 ns一個點,這樣的速度對于測量退相干時間為1 μs的 3D Transmon 太短,為了得到 3D Transmon 的相干振蕩,只能盡量拉長網絡分析儀的測試時間窗口,通過取平均的方法得到量子比特的相干振蕩.將中頻帶寬設定為5 Hz,對應的一個測試點時間為0.2 s,測試的時序圖如圖4所示,網絡分析儀的一次讀取包含 0.2 s/5 μs=40000 次激勵過程,通過改變微波激勵時間t,就可以得到3D Transmon的相干振蕩曲線.當微波激勵功率為–100 dBm,網絡分析儀讀取功率為–138 dBm時得到的相干振蕩幅度與相位曲線如圖5所示.

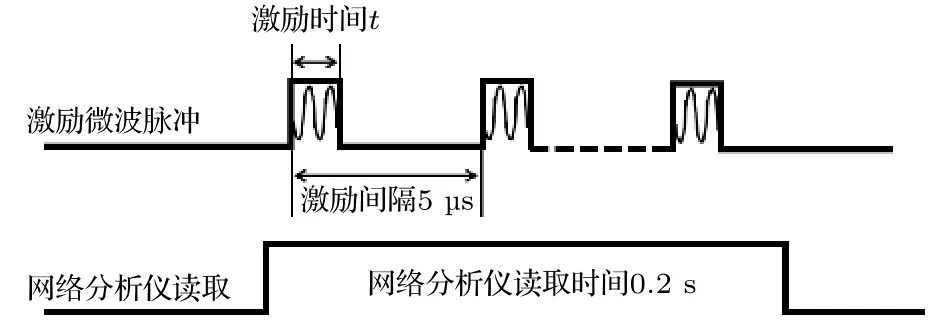
圖4 網絡分析儀測量相干振蕩時序圖Fig.4.Time sequence diagram of coherent oscillation measured by network analyzer.

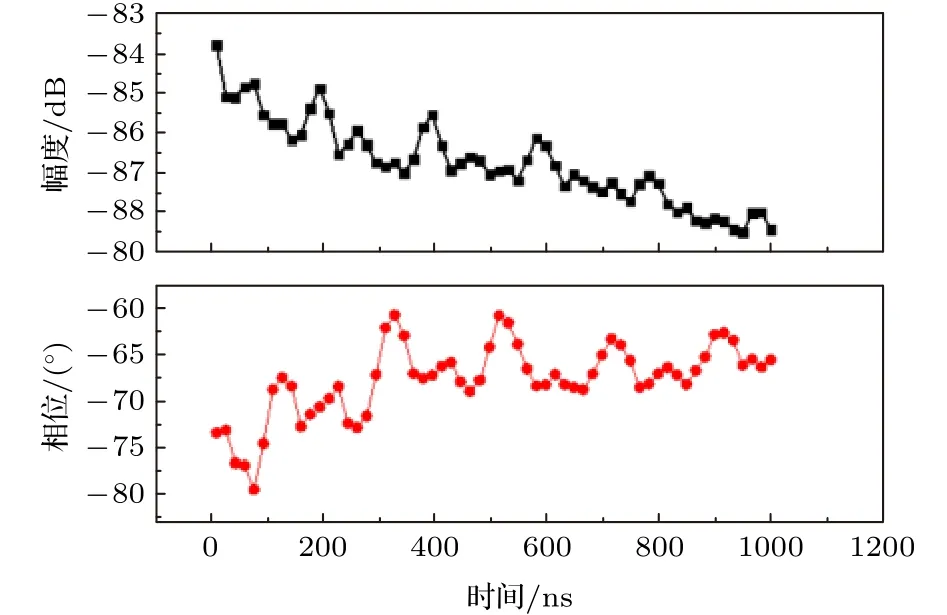
圖5 網絡分析儀測量 3D Transmon 相干振蕩幅度與相位圖Fig.5.Amplitude and phase diagram of 3D transmon coherent oscillation measured by network analyzer.

圖5可以明顯的看出3D Transmon的相干振蕩,與傳統意義的拉比振蕩所不同的是,該曲線只能看到振蕩的峰值,卻看不到振蕩的谷值,這是由于超導諧振腔的品質因數為4.8 × 105,對應的光子存儲時間約為2 μs,大于量子比特的退相干時間.測試時,用網絡分析儀持續監測 8.065 GHz 處的諧振峰,幅度曲線上的峰值代表量子比特處于基態,當量子比特處于激發態時,量子信息在還沒有離開超導諧振腔之間前已經進行了部分衰減,因此看不到振蕩曲線的波谷.從圖5的振蕩曲線來看,該3D Transmon的在微波激勵信號長度為1 μs時,曲線還在振蕩.改變微波激勵信號的功率進行測試,得到不同功率下的拉比振蕩結果如圖6(a)所示,畫出拉比振蕩與激勵微波幅度的關系圖(圖6(b)).從擬合結果來看,拉比振蕩頻率與微波激勵幅度呈現出比較好的線性關系.這也說明了通過網絡分析儀測量相干振蕩為拉比振蕩.

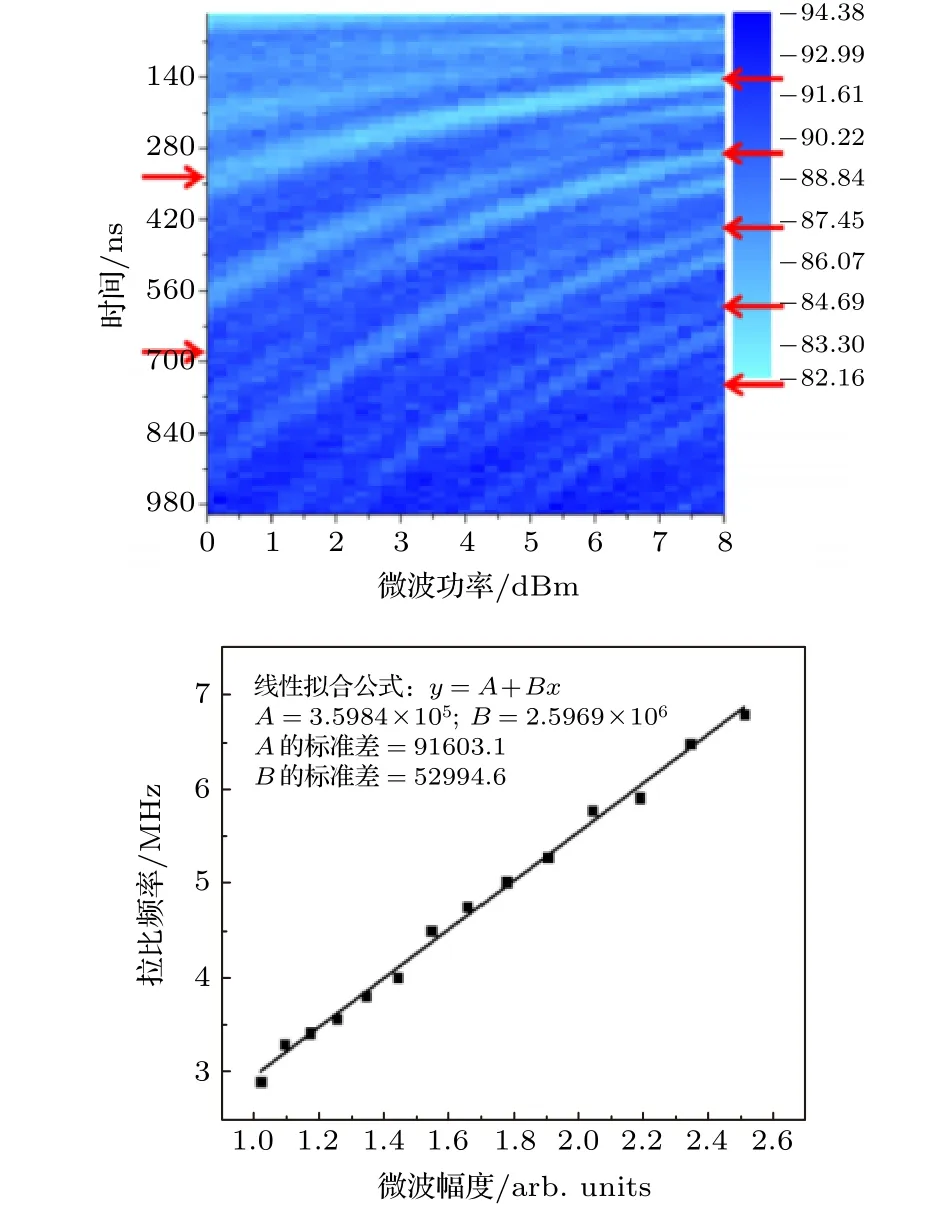
圖6 (a) 不同微波功率下的相干振蕩強度圖;(b) 相干振蕩與微波激勵幅度關系Fig.6.(a) Intensity diagram of coherent oscillation at different microwave power;(b) relationship between coherent oscillation and microwave excitation amplitude.

為了對比該方法得到的振蕩曲線與經典拉比振蕩曲線的關系,我們采用了數據采集卡Jaynes-Cummings方法測試拉比振蕩[24],如圖7所示,得到的拉比振蕩時間為1151.8 ns.

通過對比發現網絡分析儀色散法得到的拉比振蕩時間較短,其主要原因是: 1)網絡分析儀測試拉比振蕩是持續性測量,因此測試信號時刻在影響3D Transmon的退相干過程,而數據采集卡方法通過嚴格的時序控制,可在需要測試時,精準地介入;2)網絡分析儀測試方法,激勵信號的周期為5 μs,該時間段內包含量子比特有激勵的過程和沒有激勵的過程,隨著激勵時間的增長,無微波激勵的占比越來越低,而在這些沒有微波激勵的時間段內,量子比特退相干后將處于基態,也就是說沒有微波激勵的區域所占比例越高,網絡分析儀測量得到的基態所占比例越高,這就造成了網絡分析儀測量拉比振蕩得到的曲線是單邊衰減振蕩的,與標準拉比振蕩曲線不同;3)色散讀出法與超導諧振腔的品質因數非常相關,選用的超導諧振腔對微波光子的存儲時間大于3D Transmon的退相干時間,因此量子信息在還沒有離開超導諧振腔之前已部分退相干,這對于測試拉比振蕩是極為不利的.而基于數據采集卡的Jaynes-Cummings方法,量子比特的讀出功率非常高,三維超導諧振腔可以“繼承”量子比特在讀出時的狀態,因此得到的退相干時間較長.

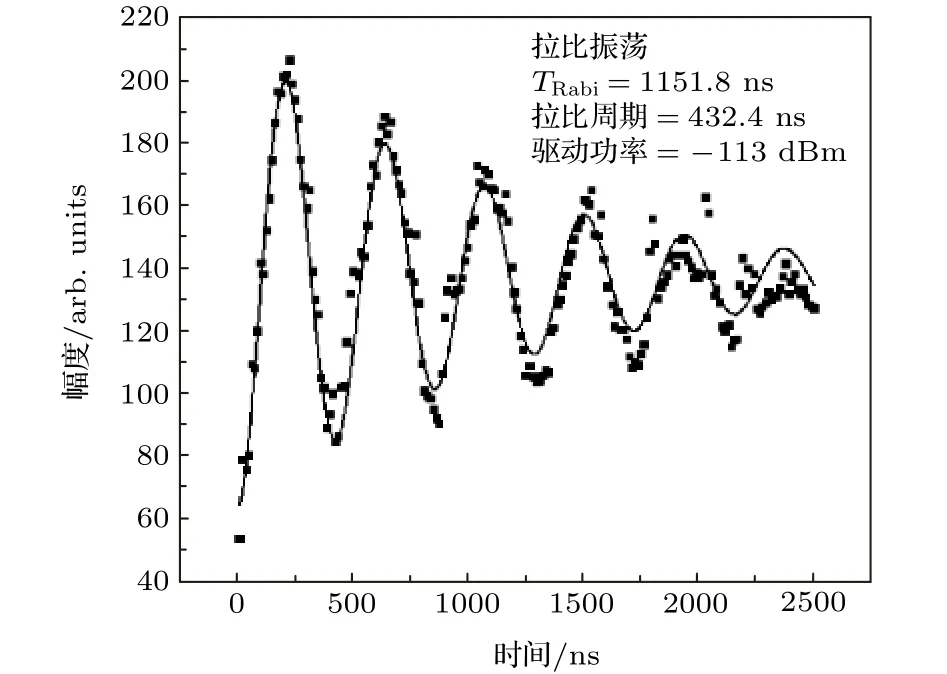
圖7 數據采集卡 Jaynes-Cummings方法測試拉比振蕩Fig.7.Rabi oscillation by Jaynes-Cummings method based on data acquisition card.

5 結 論

本文創新性地提出了一種基于網絡分析儀色散法的3D Trasnmon相干振蕩測試方法,該方法的測試系統搭建較為簡單,但由于受到諧振腔品質因數、微波激勵信號占激勵總時間比例以及持續測量的影響,網絡分析儀色散法得到的拉比振蕩時間小于數據采集卡Jaynes-Cummings方法得到時間.該方法可作為一種快速驗證量子系統是否具備時域特性的一種輔助手段,可推廣至其他量子系統.

感謝日本NEC基礎創新實驗室Tsai J S提供的樣品加工支持.