線性引力論的引力磁分量及其磁效應(yīng)

郝迪 郭三棟 馬智遠(yuǎn) 惠宇廷

(西安郵電大學(xué)電子工程學(xué)院,西安 710121)

根據(jù)廣義相對(duì)論,弱場(chǎng)近似條件下引力場(chǎng)中不僅含有經(jīng)典的牛頓引力場(chǎng),還存在一種類比于磁場(chǎng)概念的引力“磁”場(chǎng),引力磁場(chǎng)的命名借用了電動(dòng)力學(xué)中磁場(chǎng)的概念.為了研究引力磁場(chǎng)的物理性質(zhì)和它引發(fā)的一些關(guān)聯(lián)效應(yīng),本文首先從線性愛因斯坦方程出發(fā),利用相似變換的方法從方程的二級(jí)張量場(chǎng)中分解出了引力的“磁”分量并定義了引力磁場(chǎng);在此基礎(chǔ)上考慮了一種通有勻速流體的環(huán)狀微管模型,通過電動(dòng)力學(xué)的分析方法研究了遠(yuǎn)離微管區(qū)域的引力磁場(chǎng)分布特征,重點(diǎn)在計(jì)算過程中改進(jìn)了以往對(duì)這類環(huán)狀模型引力磁場(chǎng)的計(jì)算方法,表明了這類模型的引力磁場(chǎng)遠(yuǎn)場(chǎng)分布模式與磁偶極子磁場(chǎng)的遠(yuǎn)場(chǎng)分布類似;之后利用類磁場(chǎng)的性質(zhì)研究了引力磁場(chǎng)的動(dòng)力學(xué)特征,首次研究了測(cè)試粒子在線性時(shí)變引力磁場(chǎng)及余弦時(shí)變引力磁場(chǎng)中的運(yùn)動(dòng)規(guī)律,同時(shí)通過設(shè)計(jì)一種具有雙層結(jié)構(gòu)且通有加速流動(dòng)流體的環(huán)狀微管模型改進(jìn)了前人對(duì)時(shí)變引力磁場(chǎng)中引力感應(yīng)、慣性系拖曳現(xiàn)象的研究辦法,從更清晰的角度用更簡(jiǎn)單的數(shù)學(xué)通過引力電磁理論研究和展示了引力感應(yīng)現(xiàn)象和廣義相對(duì)論中的慣性系拖曳現(xiàn)象.全文為引力磁場(chǎng)及其關(guān)聯(lián)效應(yīng)的研究提供了一些新的方法和思路.

1 引 言

描述弱引力場(chǎng)規(guī)律的線性愛因斯坦方程在數(shù)學(xué)形式上是一個(gè)非齊次的波動(dòng)方程,它是愛因斯坦場(chǎng)方程在弱場(chǎng)近似條件下的結(jié)果.1918年,Lense和Thirring在求解線性愛因斯坦方程時(shí)發(fā)現(xiàn),這樣一個(gè)與電磁場(chǎng)d’Alembert方程相似的引力場(chǎng)方程若滿足適當(dāng)?shù)淖儞Q條件可以分解成與Maxwell方程內(nèi)容相似的4個(gè)獨(dú)立方程[1],它們分別對(duì)應(yīng)了電場(chǎng)和磁場(chǎng)各自的散度及旋度方程.由于從引力場(chǎng)方程中分解出了引力的磁分量,那么引力理論中便引入一種不同于牛頓引力場(chǎng)的新形式場(chǎng),將其稱作引力磁場(chǎng) (gravitomagnetic field),引力的磁效應(yīng)后來也被統(tǒng)稱作Lense-Thirring(L-T)效應(yīng)[1,2].引力磁場(chǎng)的研究熱度持續(xù)至今,人們根據(jù)引力磁場(chǎng)與經(jīng)典磁場(chǎng)的對(duì)應(yīng)關(guān)系相繼建立了“引力洛倫茲力”、“引力電動(dòng)勢(shì)”、“引力感應(yīng)”等全新的物理概念,并據(jù)此更為簡(jiǎn)便地解釋了廣義相對(duì)論的慣性系拖曳效應(yīng)[3],同時(shí)人們還設(shè)計(jì)了一系列實(shí)驗(yàn)來驗(yàn)證引力的磁效應(yīng),很多實(shí)驗(yàn)都直接或間接地證明了引力磁場(chǎng)及其連帶效應(yīng)的真實(shí)性,詳見文獻(xiàn)[4?8].

引力磁場(chǎng)是弱引力場(chǎng)問題中的一個(gè)新穎且重要的物理概念,而通過一些具體的物理模型來研究引力磁場(chǎng)的性質(zhì)是解決實(shí)際弱場(chǎng)問題的重要手段.截至目前,研究者設(shè)計(jì)了多種物理模型對(duì)引力磁場(chǎng)的空間分布模式以及動(dòng)力學(xué)效應(yīng)進(jìn)行研究.在場(chǎng)的分布模式方面,Ruggiero[2]設(shè)計(jì)了模擬太陽(yáng)系行星軌道的剛性旋轉(zhuǎn)圓環(huán)模型,研究了圓環(huán)遠(yuǎn)場(chǎng)及環(huán)內(nèi)的引力磁場(chǎng)分布情況.Mashhoon等[9]總結(jié)過低速旋轉(zhuǎn)引力源引力磁場(chǎng)分布模式的一般形式.文獻(xiàn)[10]研究了剛性旋轉(zhuǎn)球殼模型的引力磁場(chǎng),還基于開普勒軌道模型研究了大質(zhì)量旋轉(zhuǎn)環(huán)的引力磁場(chǎng).在引力磁效應(yīng)方面,Tajmar和Assis[3]通過一種旋轉(zhuǎn)球殼模型研究了引力磁場(chǎng)的磁感應(yīng)效應(yīng),該研究有助于引力磁感應(yīng)效應(yīng)在球殼類模型中的推廣.同時(shí),Bini等[11]通過一種連通圓環(huán)模型研究了引力磁感應(yīng)效應(yīng),并總結(jié)了這類感應(yīng)效應(yīng)與法拉第電磁感應(yīng)之間的差異,Tartaglia和Ruggiero[12]還研究了大質(zhì)量旋轉(zhuǎn)體的引力磁感應(yīng)效應(yīng).在動(dòng)力學(xué)性質(zhì)方面,文獻(xiàn) [11,13?15]均研究了被測(cè)物體在引力磁場(chǎng)中的運(yùn)動(dòng)規(guī)律,同時(shí)Mashhoon[16]通過一種可激發(fā)線性時(shí)變引力磁場(chǎng)的引力源模型研究了時(shí)變引力磁場(chǎng)對(duì)測(cè)試陀螺儀進(jìn)動(dòng)現(xiàn)象的影響.

然而,在以上圍繞具體模型展開的引力磁場(chǎng)及引力磁效應(yīng)的研究中,很多都存在一些不可避免的缺陷.例如Ruggiero[2]的模型是僅針對(duì)宏觀行星運(yùn)動(dòng)軌道所設(shè)計(jì)的,并沒有說明其結(jié)論是否適用于微觀或其他環(huán)狀模型的情形,且他們對(duì)環(huán)狀模型引力磁場(chǎng)遠(yuǎn)場(chǎng)分布模式的求解過程過于復(fù)雜,不具備應(yīng)用的普適性;Tajmar和Assis[3]用于研究引力磁感應(yīng)效應(yīng)的球殼模型由于結(jié)構(gòu)的復(fù)雜性而不利于內(nèi)環(huán)受力情況的分析,同時(shí)該研究缺乏對(duì)內(nèi)外閉合環(huán)路與引力感應(yīng)過程之間相關(guān)性的演示;而在引力磁場(chǎng)動(dòng)力學(xué)效應(yīng)的研究中,國(guó)內(nèi)外一直缺乏對(duì)時(shí)變引力磁場(chǎng)中粒子運(yùn)動(dòng)規(guī)律的研究,而粒子在時(shí)變引力磁場(chǎng)中的運(yùn)動(dòng)又是弱引力場(chǎng)研究中的一個(gè)重要部分.為了彌補(bǔ)舊模型的缺陷,簡(jiǎn)化以往研究過程中的復(fù)雜計(jì)算從而改進(jìn)以往的研究手段,本文基于Ruggiero[2]及 Tajmar和 Assis[3]設(shè)計(jì)的模型,建立了一類以環(huán)狀微管結(jié)構(gòu)為基礎(chǔ)的簡(jiǎn)單物理模型,這類模型受自然界中最小磁單元——磁偶極子的啟發(fā),具有可激發(fā)引力磁場(chǎng)的基本單元屬性,在引力磁效應(yīng)的研究中會(huì)更具有普適性.利用這類微管模型,本文重新研究了引力磁場(chǎng)的空間分布模式,且在此過程中極大地簡(jiǎn)化了以往對(duì)這類環(huán)狀模型引力磁場(chǎng)的計(jì)算過程,并首次對(duì)這類模型的場(chǎng)分布作了仿真,這對(duì)今后環(huán)狀模型引力磁場(chǎng)的計(jì)算和研究提供了便利.在此基礎(chǔ)上,設(shè)計(jì)了一種具有雙層結(jié)構(gòu)的微管模型,通過這種相對(duì)簡(jiǎn)單的結(jié)構(gòu),利用比Tajmar和Assis[3]設(shè)計(jì)的球殼模型更為簡(jiǎn)單的數(shù)學(xué)研究了引力磁感應(yīng)效應(yīng),并據(jù)此更為方便地解釋了引力電磁理論背景下的慣性系拖曳現(xiàn)象,有望為地面實(shí)驗(yàn)室中研究引力磁感應(yīng)現(xiàn)象及慣性系拖曳現(xiàn)象提供便利的理論基礎(chǔ).除此之外,本文還首次研究了中性粒子在線性時(shí)變及余弦時(shí)變引力磁場(chǎng)中的運(yùn)動(dòng)軌跡,從而彌補(bǔ)了以往引力磁場(chǎng)動(dòng)力學(xué)研究中關(guān)于粒子運(yùn)動(dòng)方面的缺陷.

2 引力的磁效應(yīng)

2.1 引力場(chǎng)方程中的引力磁分量

廣義相對(duì)論中,引力場(chǎng)的愛因斯坦方程寫作[17]

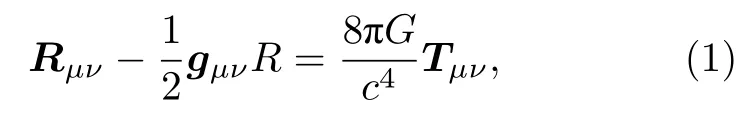
其中,Rμν是描述時(shí)空彎曲程度的里奇張量,Tμν代表物質(zhì)場(chǎng)的能動(dòng)張量,G為引力常數(shù),c為光速.時(shí)空近似平直 (gμν=ημν+γμν) 時(shí),采用弱場(chǎng)近似條件[17],(1)式將退化成一個(gè)線性偏微分方程,表示為

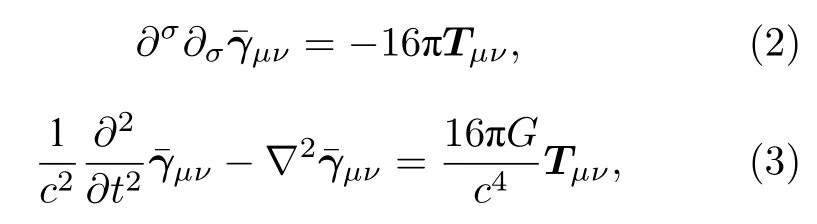
令物質(zhì)場(chǎng)的能動(dòng)張量為一個(gè)4維行向量,表示為

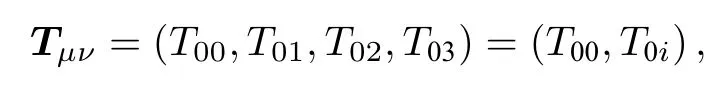
其中,T00=ρmc2代表能量密度,T0i=?jmc(i=1,2,3)代表能流密度.同時(shí)令二級(jí)張量場(chǎng)γˉμν也為一個(gè)4維行向量,表示為

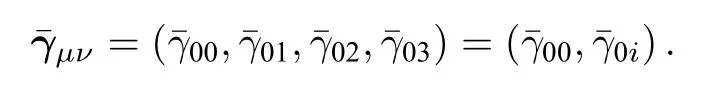
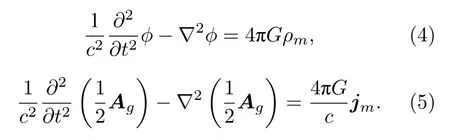
顯然,(4)式及(5)式分別對(duì)應(yīng)了電動(dòng)力學(xué)中電磁場(chǎng)標(biāo)勢(shì)和矢勢(shì)所滿足的波動(dòng)方程,此時(shí)引力場(chǎng)的類電磁學(xué)性質(zhì)已經(jīng)顯現(xiàn)出來.進(jìn)一步可用引力場(chǎng)的廣義標(biāo)勢(shì)和廣義矢勢(shì)定義引力場(chǎng)的兩個(gè)場(chǎng)量如下:

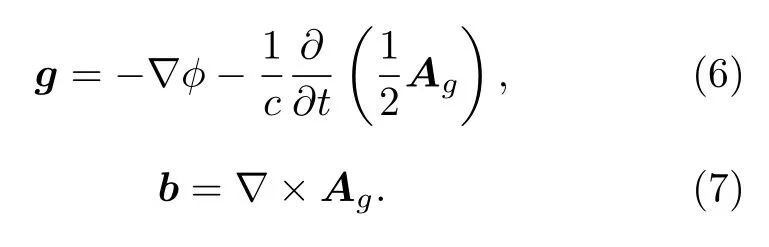
采用常見的洛倫茲規(guī)范條件,(4)式及(5)式將分解成Maxwell方程的基本形式,表示為

方程(8a)—(8d)就是引力電磁理論(gravitoelectromagnetism,GEM)的 4 個(gè)基本方程,本文得到的結(jié)論與Mironov和Mironov[18]以及Demir[19]給出的結(jié)論在形式上基本一致,而內(nèi)容上的差異源于對(duì)廣義標(biāo)勢(shì)和廣義矢勢(shì)定義的不同,不同的定義方式得到的結(jié)論會(huì)有所差別.從類比角度來看,方程中的b就是對(duì)應(yīng)于磁場(chǎng)概念的引力磁場(chǎng).從 (8a)式—(8d)式分析中可知,b是對(duì)引力場(chǎng)廣義矢勢(shì)旋度的結(jié)果,而引力場(chǎng)廣義矢是線性愛因斯坦方程場(chǎng)量空間分所以引力磁場(chǎng)可見引力磁場(chǎng)就是場(chǎng)量的一個(gè)分量,它是線性引力論的一個(gè)特有結(jié)果.

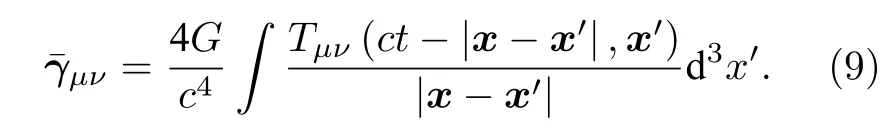
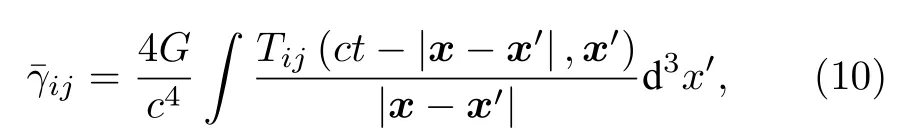
當(dāng)引力源由一種具有限定范圍且運(yùn)動(dòng)緩慢的松散物質(zhì)組成時(shí),那么其能動(dòng)張量的i,j分量表示為Tij～ρmvivj+pδij[20],其中p為應(yīng)力.由于物質(zhì)源的運(yùn)動(dòng)緩慢,所以|v|?c,再考慮到物質(zhì)為松散介質(zhì),所以應(yīng)力p在數(shù)量級(jí)上也遠(yuǎn)小于光速c,則那么根據(jù) (10)式,此時(shí)這些無窮小項(xiàng)就可以忽略不計(jì)[20].所以總結(jié)為,當(dāng)所研究的引力源滿足①具有限定范圍;②運(yùn)動(dòng)速度緩慢,|v|?c;③應(yīng)力p數(shù)量級(jí)很小的條件時(shí),可以不考慮含c?4的無窮小場(chǎng)量,那么此時(shí)的張量場(chǎng)將表示為

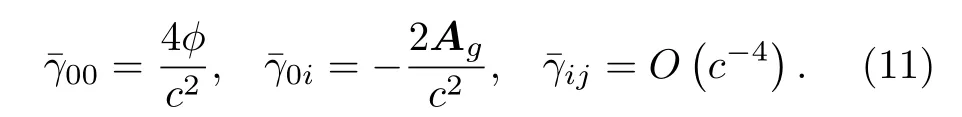
在略去O(c?4) 的條件下,表征GEM理論的(8)式便是成立的.而對(duì)于地面實(shí)驗(yàn)室環(huán)境,地球系統(tǒng)以及太陽(yáng)系等弱引力場(chǎng)情形而言,這類限定條件總是滿足的,這也是可以利用空間實(shí)驗(yàn)及地面實(shí)驗(yàn)來驗(yàn)證引力磁效應(yīng)的原因.

2.2 引力磁場(chǎng)及其關(guān)聯(lián)效應(yīng)的實(shí)驗(yàn)驗(yàn)證

對(duì)引力磁場(chǎng)及引力磁效應(yīng)的實(shí)驗(yàn)驗(yàn)證是證明廣義相對(duì)論正確的一個(gè)途徑,也是表明引力磁場(chǎng)具備可研究意義的必要條件.這類驗(yàn)證最初是通過以GP-B實(shí)驗(yàn)衛(wèi)星為首的空間實(shí)驗(yàn)展開的,其主要的一個(gè)目標(biāo)就是以預(yù)期1%的精度驗(yàn)證廣義相對(duì)論中的慣性系拖曳效應(yīng)[4,5].這種慣性系拖曳體現(xiàn)為旋轉(zhuǎn)引力源會(huì)對(duì)其周圍的慣性參考系產(chǎn)生拖曳力,其強(qiáng)度與引力源的自轉(zhuǎn)角動(dòng)量(或角速度)成正比關(guān)系.因?yàn)閼T性系拖曳可以看作是慣性系質(zhì)點(diǎn)受到了轉(zhuǎn)動(dòng)參考系中科里奧利力的作用,根據(jù)等效原理這種慣性力對(duì)應(yīng)于電動(dòng)力學(xué)中被測(cè)電荷受到的磁洛倫茲力,所以轉(zhuǎn)動(dòng)參考系的角速度就對(duì)應(yīng)了磁場(chǎng)的概念,這也是將引力磁場(chǎng)與轉(zhuǎn)動(dòng)參考系角速度相關(guān)聯(lián)的一個(gè)原因,本文4.1節(jié)中關(guān)于測(cè)試粒子在弱引力場(chǎng)中運(yùn)動(dòng)規(guī)律的內(nèi)容對(duì)這一點(diǎn)作了進(jìn)一步說明.GP-B實(shí)驗(yàn)衛(wèi)星的目的就是想通過測(cè)量慣性系拖曳的結(jié)果來驗(yàn)證引力磁效應(yīng),從而驗(yàn)證廣義相對(duì)論的正確性,但因?yàn)閷?shí)驗(yàn)最終的精度只控制到了19%[4],并沒有達(dá)到預(yù)期的1%,所以整個(gè)實(shí)驗(yàn)的結(jié)論并沒有得到廣泛的認(rèn)可.而截至目前,能夠精準(zhǔn)表明引力磁場(chǎng)及引力磁效應(yīng)真實(shí)存在的證據(jù)可以體現(xiàn)在以下幾個(gè)實(shí)驗(yàn)和推論當(dāng)中:

1)比較受關(guān)注的一項(xiàng)實(shí)驗(yàn)是由Tajmar等[8]進(jìn)行的液氦低溫超導(dǎo)鈮環(huán)旋轉(zhuǎn)實(shí)驗(yàn),這是研究人員首次在地面實(shí)驗(yàn)室中檢測(cè)到了可測(cè)量性的引力磁場(chǎng),該實(shí)驗(yàn)也受到了GP-B實(shí)驗(yàn)衛(wèi)星負(fù)責(zé)人Everitt的肯定[21].根據(jù) de Matos和 Tajmar[22]的理論,超導(dǎo)鈮環(huán)中的引力子由于獲得了質(zhì)量從而使旋轉(zhuǎn)的鈮環(huán)能夠產(chǎn)生比以往更強(qiáng)的引力磁場(chǎng).研究者將鈮環(huán)置于液氦低溫環(huán)境下,利用伺服電機(jī)驅(qū)動(dòng)鈮環(huán)做繞中心軸旋轉(zhuǎn)的加速運(yùn)動(dòng),同時(shí)在鈮環(huán)附近多個(gè)位置放置了粒子加速度計(jì)用以計(jì)量拖曳力,實(shí)驗(yàn)結(jié)果顯示加速度計(jì)受到了強(qiáng)烈的拖曳力,檢測(cè)到的加速度場(chǎng)的平均值是噪聲(干擾信號(hào))的3.3倍以上.現(xiàn)普遍認(rèn)為 de Matos的理論是正確的,該實(shí)驗(yàn)同時(shí)也驗(yàn)證了引力磁場(chǎng)及慣性系拖曳現(xiàn)象的真實(shí)性[8];

2)另一項(xiàng)能夠驗(yàn)證引力磁效應(yīng)的實(shí)驗(yàn)是中子–引力干涉實(shí)驗(yàn).最早由Aharonov與Carmi[23]根據(jù)等效原理提出引力體系中存在類似于Aharonov-Bohm(A-B)效應(yīng)的Aharonov-Carmi(A-C)效應(yīng),即在旋轉(zhuǎn)坐標(biāo)系中沿閉合路徑傳播的物質(zhì)波將獲得一個(gè)幾何相位因子,該相位因子與旋轉(zhuǎn)坐標(biāo)系的角速度相關(guān),在GEM理論中這個(gè)相位因子就與引力磁場(chǎng)有關(guān).Overhauser與Colella[24]根據(jù)這種推論設(shè)計(jì)了中子–引力干涉實(shí)驗(yàn),用于證明中子物質(zhì)波的A-C效應(yīng),由此也能證明引力磁場(chǎng)的真實(shí)性.后來研究者們利用理想晶體硅干涉儀,在一系列中子干涉實(shí)驗(yàn)中觀測(cè)到了大質(zhì)量粒子在引力磁場(chǎng)作用下的幾何相移[25],并通過分析干涉儀自身彈性形變引起的系統(tǒng)效應(yīng)排除了實(shí)驗(yàn)誤差,進(jìn)一步確定了A-C效應(yīng)的正確性和GEM理論的正確性;

3)最近一項(xiàng)關(guān)于慣性系拖曳現(xiàn)象的重要實(shí)驗(yàn)是由Krishnan等[26]對(duì)脈沖雙星系統(tǒng)PSR J1141-6545的研究而展開的,該實(shí)驗(yàn)從脈沖雙星系統(tǒng)中觀測(cè)到了比GP-B實(shí)驗(yàn)衛(wèi)星更為顯著的慣性系拖曳效應(yīng).研究者通過脈沖計(jì)時(shí)法發(fā)現(xiàn)了PSR J1141-6545系統(tǒng)軌道參數(shù)發(fā)生的漂移現(xiàn)象,為了解釋該現(xiàn)象,Krishnan等[26]將廣義相對(duì)論的L-T進(jìn)動(dòng)效應(yīng)的影響引入到系統(tǒng)中,因此這類表征軌道參數(shù)漂移的數(shù)據(jù)得到了很好的解釋.通過大量的數(shù)值模擬,實(shí)驗(yàn)最終表明從這類脈沖雙星系統(tǒng)中觀測(cè)到了較為明顯的慣性系拖曳現(xiàn)象,也從很好的精度上證實(shí)了慣性系拖曳現(xiàn)象的正確性,彌補(bǔ)了GP-B實(shí)驗(yàn)衛(wèi)星精度性差的缺陷,同時(shí)再次證明了廣義相對(duì)論的正確性.對(duì)慣性系拖曳現(xiàn)象的證明也說明了引力磁場(chǎng)及其關(guān)聯(lián)效應(yīng)的真實(shí)性,這一點(diǎn)也將促進(jìn)人們對(duì)引力磁場(chǎng)的研究.

對(duì)以往驗(yàn)證引力磁場(chǎng)及其關(guān)聯(lián)效應(yīng)的實(shí)驗(yàn)作了討論后,本文重點(diǎn)關(guān)注地面實(shí)驗(yàn)室中對(duì)引力磁效應(yīng)的研究.根據(jù) Tajmar和 de Matos[27]已有的實(shí)驗(yàn)結(jié)論以及建議,我們將試圖建立一些通有超流體的簡(jiǎn)單環(huán)狀微管模型來研究引力磁場(chǎng)及其關(guān)聯(lián)效應(yīng)的性質(zhì),從而為在地面實(shí)驗(yàn)室中研究引力磁效應(yīng)提供一些可行的思路和辦法.

3 通有勻速流體的環(huán)狀微管的引力磁場(chǎng)

3.1 環(huán)狀微管模型的引力磁場(chǎng)遠(yuǎn)場(chǎng)分布

本節(jié)研究勻速旋轉(zhuǎn)圓環(huán)的引力磁場(chǎng)遠(yuǎn)場(chǎng)(遠(yuǎn)離場(chǎng)源中心的任意點(diǎn)位置)分布表達(dá)式.選定勻速旋轉(zhuǎn)圓環(huán)模型作為研究對(duì)象的原因在于,電動(dòng)力學(xué)中由小尺度閉合環(huán)電流構(gòu)成的簡(jiǎn)單磁偶極子單元是自然界中最基本的磁單元,同樣也是靜磁場(chǎng)研究中的一個(gè)重要物理模型.假定勻速旋轉(zhuǎn)圓環(huán)模型也是靜引力磁場(chǎng)的一種基本單元,從這種基本單元出發(fā)可以通過疊加原理得到任何形式的引力磁場(chǎng)分布.

為此,本文設(shè)計(jì)了如圖1所示的圓環(huán)模型,需要說明的是由于在實(shí)驗(yàn)上不易實(shí)現(xiàn)圓環(huán)剛體繞其軸心穩(wěn)定旋轉(zhuǎn),所以本文改用向環(huán)狀微管內(nèi)通入勻速流動(dòng)的均勻流體(或超流體[27])來等效勻速旋轉(zhuǎn)圓環(huán)模型(后簡(jiǎn)稱微管模型).

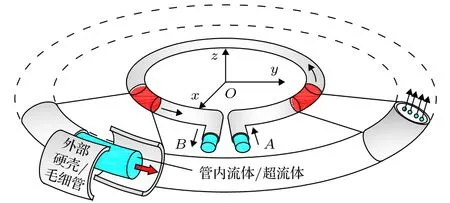
圖1 通有勻速流體的環(huán)狀微管模型Fig.1.The circular microtube model with uniform velocity fluids.

本節(jié)旨在得到微管模型引力磁場(chǎng)的遠(yuǎn)場(chǎng)分布表達(dá)式從而研究其空間分布特征.前面的分析中已經(jīng)定義了引力場(chǎng)的廣義矢勢(shì),而通過求廣義矢勢(shì)Ag的旋度就可以得到引力磁場(chǎng)b的數(shù)學(xué)表達(dá)式,所以針對(duì)引力磁場(chǎng)的求解要依賴于廣義矢勢(shì)Ag.方程(5)所對(duì)應(yīng)的希爾伯特推遲解為

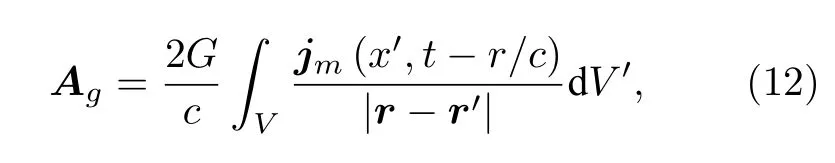
在一維環(huán)路上,該推遲解用閉合環(huán)路積分表示為

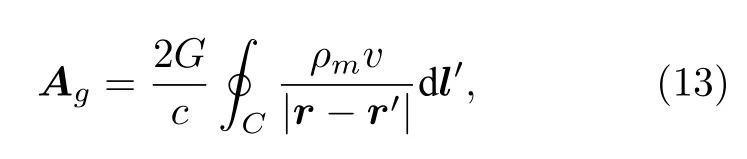
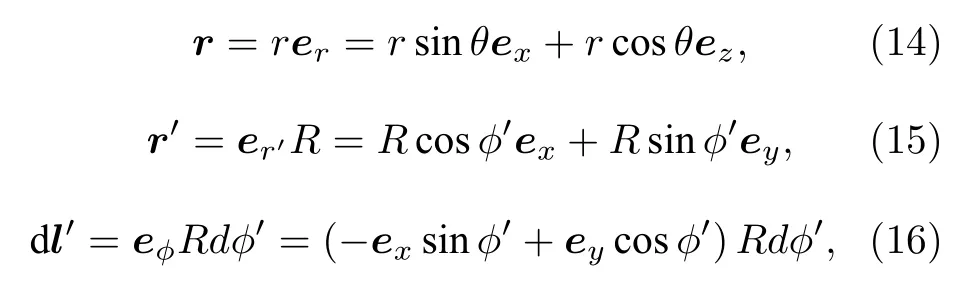
則根據(jù) (14)式及 (15)式,|r?r′|可以表示為

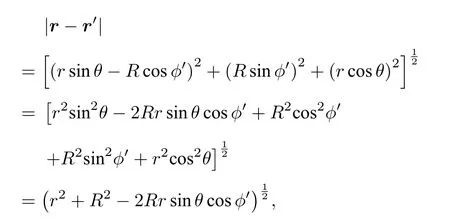
進(jìn)一步,得到其倒數(shù)形式為

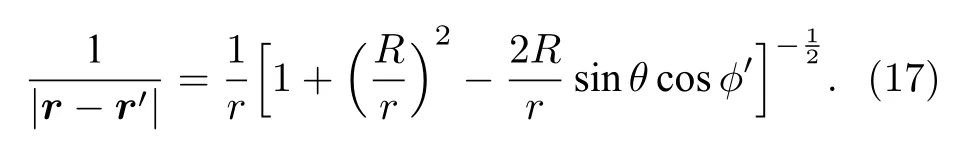
在遠(yuǎn)場(chǎng)區(qū)考慮到r?R,則(17)式中的項(xiàng)可略去,則有

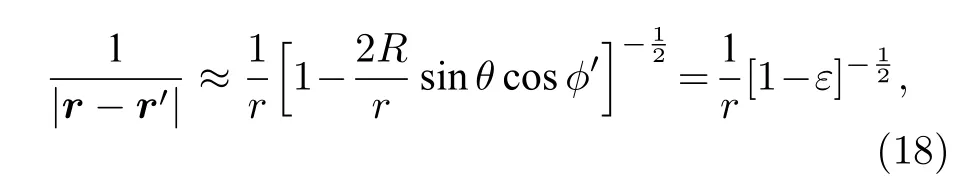
對(duì)(18)式應(yīng)用廣義二項(xiàng)式定理展開,有

略去含ε2項(xiàng)及其之后的所有無窮小項(xiàng),只保留(19)式的前兩項(xiàng),則有

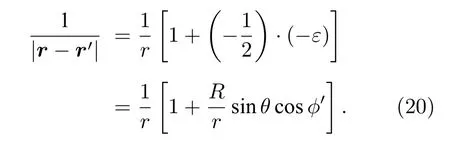
將(16)式及(20)式代入(13)式中,引力磁矢勢(shì)表示為

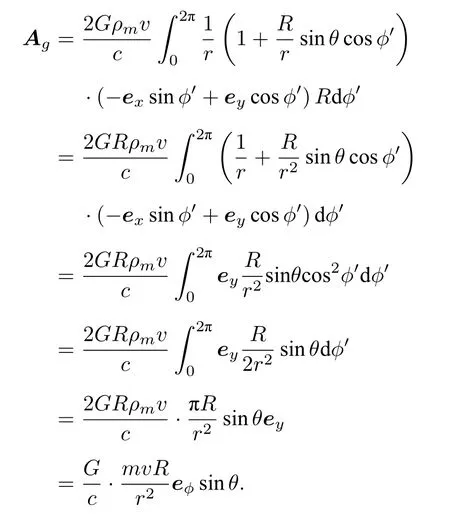
定義微管內(nèi)流體的旋轉(zhuǎn)角動(dòng)量為L(zhǎng)=mvR,則引力磁矢勢(shì)用含角動(dòng)量的形式表示為

利用引力磁場(chǎng)與引力磁矢勢(shì)的關(guān)系b=?×Ag,計(jì)算直角坐標(biāo)系下微管模型的遠(yuǎn)場(chǎng)區(qū)域引力磁場(chǎng)分布為

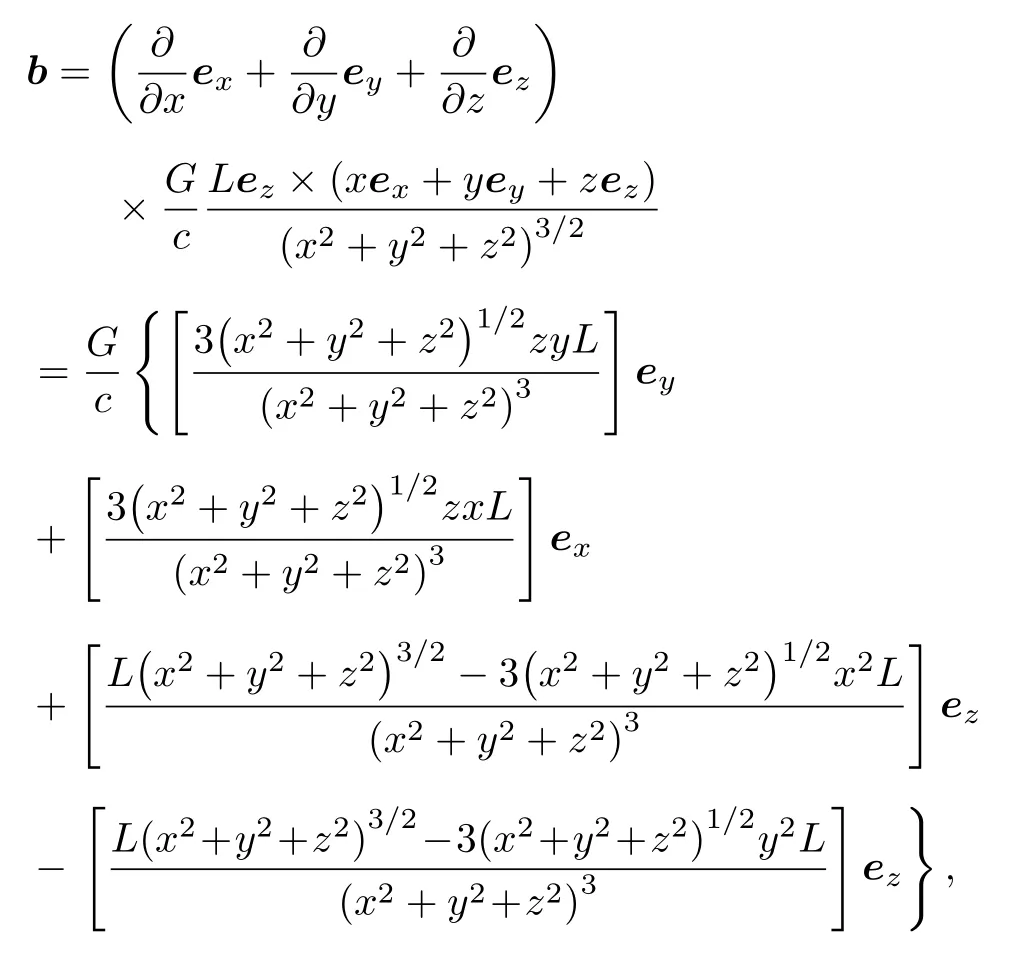
在此基礎(chǔ)上,用矢徑r及其模值代替上式中各分量的內(nèi)容,有

(22)式是基于對(duì)小尺度環(huán)狀微管模型引力磁場(chǎng)遠(yuǎn)場(chǎng)分布模式的求解結(jié)果,與Ruggiero[2]對(duì)大尺度質(zhì)量環(huán)模型引力磁場(chǎng)遠(yuǎn)場(chǎng)分布模式的計(jì)算結(jié)果類似.而這兩類結(jié)果的異同之處則體現(xiàn)在以下幾個(gè)方面:

1)模型的目標(biāo)和適用性不同: Ruggiero[2]的結(jié)論是針對(duì)宏觀行星模型的運(yùn)動(dòng)軌道所得到的引力磁場(chǎng)遠(yuǎn)場(chǎng)分布模式,并未說明這類計(jì)算結(jié)果是否適用于微觀或其他環(huán)狀模型的情形,是否能夠解釋其他形式引力磁場(chǎng)的產(chǎn)生機(jī)制;而(22)式是考慮了一種普遍的可以激發(fā)引力磁場(chǎng)的最小引力磁單元—小尺度閉合微管模型,相比于大質(zhì)量環(huán)模型,這種類磁偶極子的微觀模型作為本文所假設(shè)的基本引力磁單元在引力磁效應(yīng)的研究中更具有普適性;

2)方程的物理內(nèi)容不同: 在Ruggiero[2]的結(jié)論中,與(22)式相似的遠(yuǎn)場(chǎng)結(jié)果表示為[2,9]

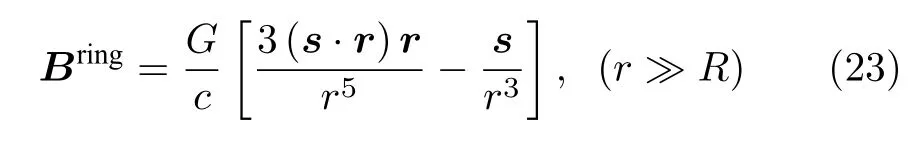
其表征了距離中心天體R處的圓形軌道上由于物體運(yùn)動(dòng)產(chǎn)生的遠(yuǎn)場(chǎng)區(qū)的引力磁場(chǎng).式中的s表示圓形軌道上運(yùn)動(dòng)物體的角動(dòng)量,其單位模值為|s0|=s0=vR,v為運(yùn)動(dòng)物體的軌道線速度;而在(22)式中,取代s的物理量為微管中流體流動(dòng)產(chǎn)生的相對(duì)于圓環(huán)中心的角動(dòng)量L,其單位模值也為vR,但v作為流體的流速可以被人為調(diào)節(jié),從而可以實(shí)現(xiàn)對(duì)引力磁場(chǎng)強(qiáng)度的調(diào)控;

3)方程的求解過程不同: (22)式的求解過程避免了在求解引力磁矢勢(shì)Ag的過程中對(duì)復(fù)雜分式的直接積分,這一點(diǎn)是對(duì)Ruggiero[2]做法的一個(gè)改進(jìn).如 (13)式—(20)式所示,本文采用了“先近似,后積分”的辦法,先對(duì)復(fù)雜分式作近似處理,再對(duì)簡(jiǎn)化后的分式進(jìn)行簡(jiǎn)單積分.整個(gè)求解過程相比傳統(tǒng)的求解過程降低了復(fù)雜程度,縮短了計(jì)算過程.

單從數(shù)學(xué)形式上來看,(22)式類比于磁偶極子磁場(chǎng)在遠(yuǎn)場(chǎng)空間的分布表達(dá)式,所以從定量角度出發(fā)可以認(rèn)為在場(chǎng)的空間分布模式上,通有勻速流體的環(huán)狀微管模型很好地對(duì)應(yīng)了磁偶極子模型.

3.2 微管模型的引力磁場(chǎng)空間分布特征

根據(jù)微管模型的引力磁場(chǎng)遠(yuǎn)場(chǎng)分布表達(dá)式以及微管模型與磁偶極子模型的對(duì)應(yīng)關(guān)系可以進(jìn)一步繪制其引力磁場(chǎng)在全空間的分布圖像,從而直觀地表達(dá)微管模型的引力磁場(chǎng)空間分布特征.如圖2所示,本文通過仿真手段繪制了微管模型y-z平面(與微管垂直的平面)的引力磁力線分布圖,x-y平面(與微管平行的平面)的引力磁場(chǎng)強(qiáng)度色譜圖以及相應(yīng)的三維函數(shù)圖像.從仿真圖像反映出的信息能夠觀察到,這種特殊的分布模式與磁偶極子磁場(chǎng)的分布模式類似,本文認(rèn)為不論是從定量關(guān)系出發(fā)還是從定性關(guān)系出發(fā)都可以認(rèn)為微管模型很好地對(duì)應(yīng)了磁偶極子模型,這與Ruggiero[2]得到的結(jié)論基本一致.

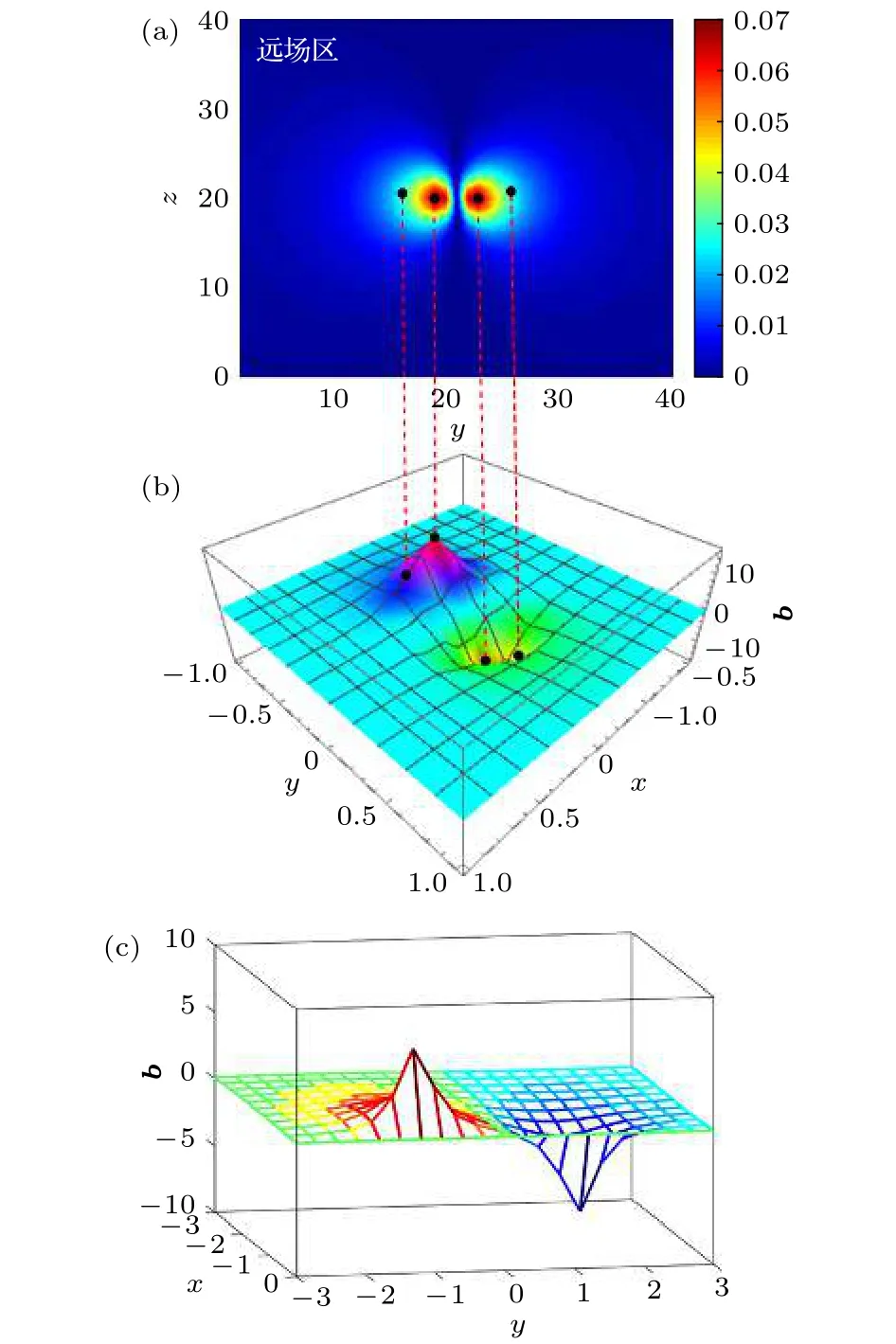
圖2 微管模型引力磁場(chǎng)遠(yuǎn)場(chǎng)分布特征 (a) 微管模型y-z平面沿y方向的引力磁場(chǎng)分布色譜圖;(b) 微管模型x-y平面沿y方向的引力磁場(chǎng)強(qiáng)度分布特征圖;(c) 微管模型x-y平面沿y方向上引力磁場(chǎng)強(qiáng)度隨y坐標(biāo)軸的變化曲線Fig.2.The far-field distribution of GM field in the microtube model: (a) The intensity plots of GM field's along y-direction in y-z plane of microtube model;(b) the distribution of GM field's along y-direction in x-y plane of microtube model;(c) the b-y function along y-direction in x-y plane of microtube model.

從圖2(a)的色譜仿真上可以看到微管模型yz平面沿y方向上的引力磁場(chǎng)分布特征.可以看到在遠(yuǎn)場(chǎng)區(qū)中,y方向上引力磁場(chǎng)的強(qiáng)度是從微管邊緣向遠(yuǎn)場(chǎng)區(qū)域逐步衰減的,再結(jié)合圖2(c)的曲線可以看到這種衰減速度很快.對(duì)應(yīng)到(22)式所表征的引力磁場(chǎng)遠(yuǎn)場(chǎng)分布表達(dá)式,代入L=Lez,r=xex+yey+zez,L·r=Lz,(22)式可分解為

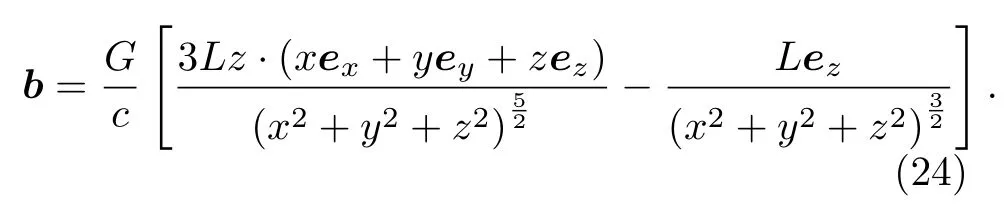
令x=0 ,則得到y(tǒng)-z平面的引力磁場(chǎng)分布

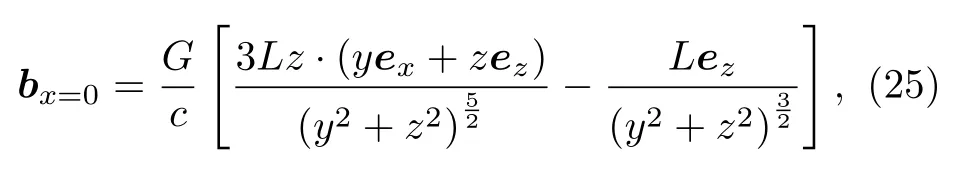
再令z=0 ,得到微管模型y-z平面沿y方向上的引力磁場(chǎng)

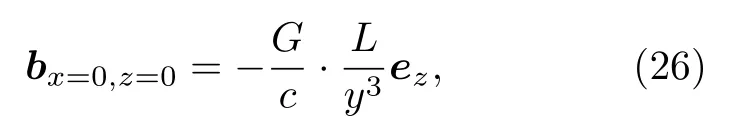
類似地,根據(jù)圖2(b)所示的仿真圖像可以研究x-y平面的引力磁場(chǎng)分布特征,可以看到引力磁場(chǎng)的強(qiáng)度同樣也是從微管邊緣向遠(yuǎn)場(chǎng)區(qū)域逐步衰減的.對(duì)應(yīng)到(22)式所表征的引力磁場(chǎng)遠(yuǎn)場(chǎng)分布表達(dá)式,代入L=Lex,L·r=Lz,(22)式可寫成

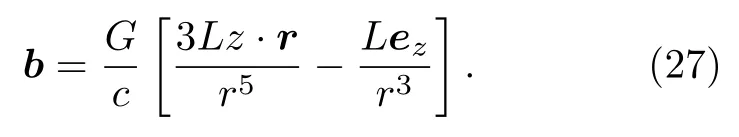
令z=0 ,則得到x-y平面的引力磁場(chǎng)分布

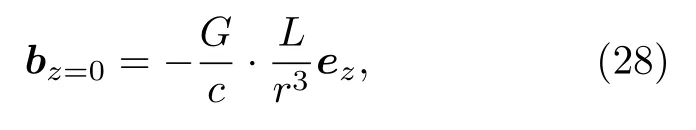
另外,從圖2(b)及圖2(c)的仿真圖像上可以研究微管環(huán)內(nèi)部引力磁場(chǎng)的分布特征,可以看到在x-y平面沿y方向上,引力磁場(chǎng)的強(qiáng)度在環(huán)內(nèi)從環(huán)邊緣向圓心處逐步遞減,圓心處的場(chǎng)強(qiáng)為環(huán)內(nèi)部的最小值,數(shù)值為零.不論是環(huán)外還是環(huán)內(nèi),引力磁場(chǎng)的衰減程度都比較劇烈,引力磁場(chǎng)的最大值總是出現(xiàn)在微管的邊緣附近.

4 引力磁場(chǎng)的動(dòng)力學(xué)特征及動(dòng)力學(xué)效應(yīng)

4.1 測(cè)試粒子在弱引力場(chǎng)中的運(yùn)動(dòng)

測(cè)試粒子在弱引力場(chǎng)中的運(yùn)動(dòng)是引力磁場(chǎng)動(dòng)力學(xué)效應(yīng)的一個(gè)重要的研究?jī)?nèi)容.在轉(zhuǎn)動(dòng)坐標(biāo)參考系下,一個(gè)測(cè)試粒子(質(zhì)荷)將受到慣性離心力和科里奧利力 (Coriolis force)這兩種慣性力[28],而在2.2節(jié)中提到的A-C效應(yīng)就是粒子動(dòng)量與旋轉(zhuǎn)參考系之間的相互作用,該作用本質(zhì)上歸結(jié)于運(yùn)動(dòng)物質(zhì)所受到的科里奧利力[29].A-C效應(yīng)中的科里奧利力類比于A-B效應(yīng)中的洛倫茲力(磁場(chǎng)力),根據(jù)等效原理可認(rèn)為科里奧利力就是測(cè)試粒子在引力磁場(chǎng)中的受力,其中轉(zhuǎn)動(dòng)坐標(biāo)系的旋轉(zhuǎn)角速度ω對(duì)應(yīng)了引力磁場(chǎng)b.這也就說明在引力磁場(chǎng)中,運(yùn)動(dòng)的粒子將受到一種類似于磁洛倫茲力的引力洛倫茲力.

現(xiàn)設(shè)定一個(gè)物理場(chǎng)景,一個(gè)質(zhì)量為m的中子作為測(cè)試粒子以相對(duì)轉(zhuǎn)動(dòng)參考系為v的速度進(jìn)入到參考系中,參考系的旋轉(zhuǎn)角速度為ω,則中子受到的慣性力為

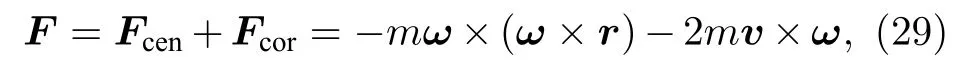
其中,Fcen為慣性離心力,Fcor為科里奧利力.參考Mashhoon等[30]的做法,根據(jù)等效原理令b=?2ω,則試探粒子受到的引力洛倫茲力可以表示為

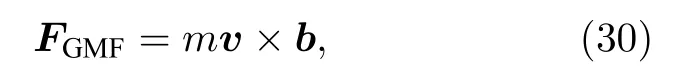
所以,在弱引力場(chǎng)中描述測(cè)試粒子的運(yùn)動(dòng)方程可以表示為:

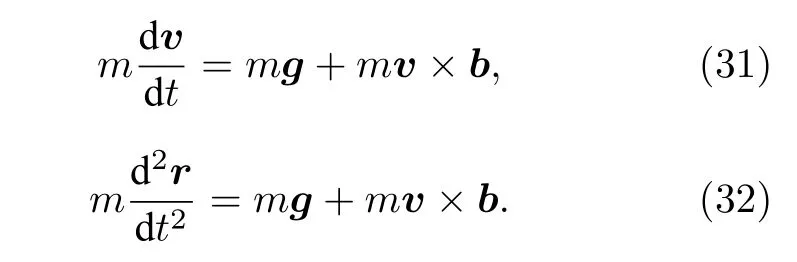
而另外一個(gè)重要的引力磁效應(yīng)——引力磁場(chǎng)的耦合效應(yīng),其本質(zhì)上是自旋粒子與轉(zhuǎn)動(dòng)參考系之間的相互作用[29],即在引力磁場(chǎng)b是時(shí)變的前提下,固定在參考系上的粒子波(物質(zhì)波)將產(chǎn)生一個(gè)與自旋相關(guān)的幾何相位因子.因此,我們考慮研究測(cè)試粒子在時(shí)變引力磁場(chǎng)中的運(yùn)動(dòng)規(guī)律,并繪制粒子在時(shí)變引力磁場(chǎng)中的運(yùn)動(dòng)軌跡,因?yàn)檫@可能對(duì)引力磁場(chǎng)的探測(cè)起到有效作用.在時(shí)空中,經(jīng)典牛頓引力場(chǎng)和引力磁場(chǎng)在直角坐標(biāo)系下展開后表示為:位矢r與速度v在直角坐標(biāo)系下表示為:

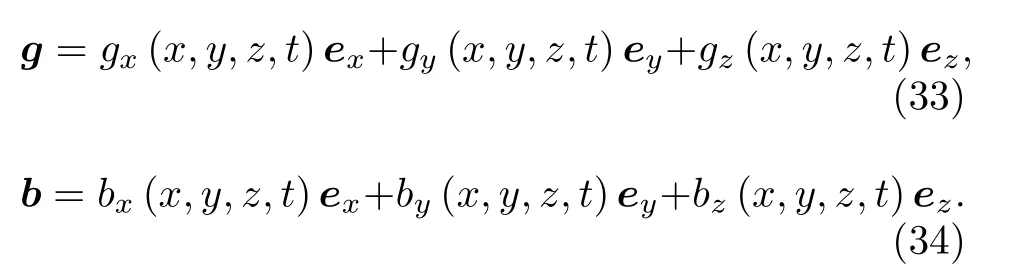
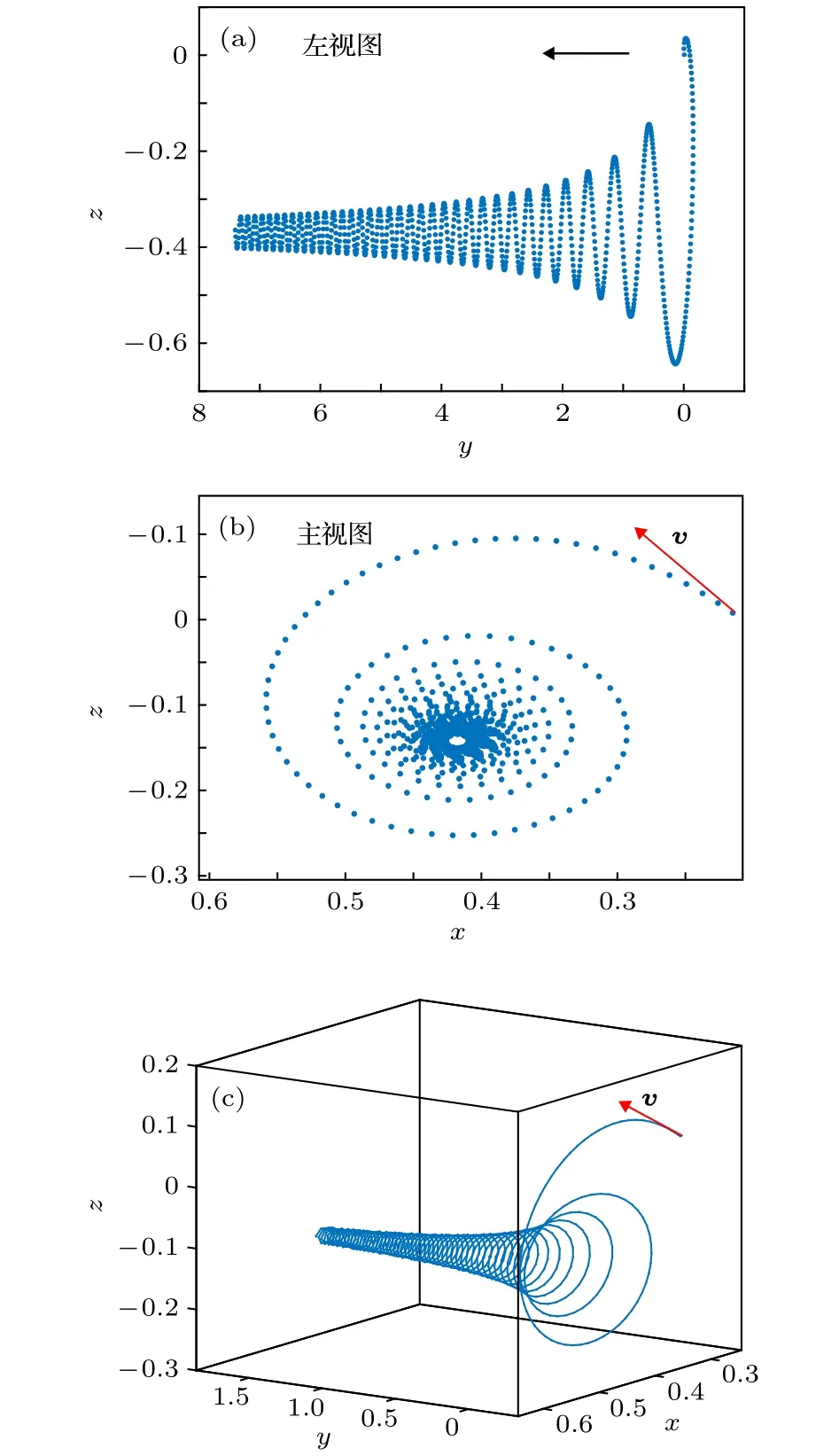
圖3 模式一下測(cè)試粒子的運(yùn)動(dòng)軌跡 (a) 測(cè)試粒子在線性時(shí)變引力磁場(chǎng)中運(yùn)動(dòng)軌跡的左視圖;(b) 測(cè)試粒子在線性時(shí)變引力磁場(chǎng)中運(yùn)動(dòng)軌跡的主視圖;(c) 測(cè)試粒子在線性時(shí)變引力磁場(chǎng)中的全空間運(yùn)動(dòng)軌跡Fig.3.The test-particle's track in linear time-varying GM field: (a) The left view of the test-particle's track;(b) the main view of the test-particle's track;(c) the test-particle's track in the whole space.

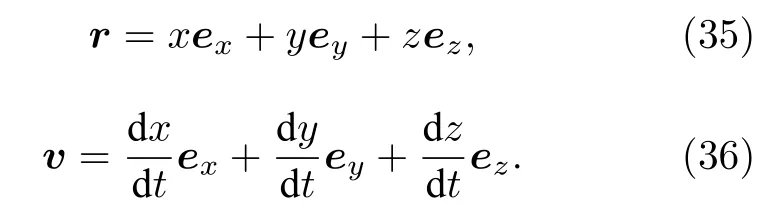
將(33)式、(34)式及(35)式代入(32)式中,測(cè)試粒子在弱引力場(chǎng)中沿各空間分量x,y,z方向的動(dòng)力學(xué)方程表示為:

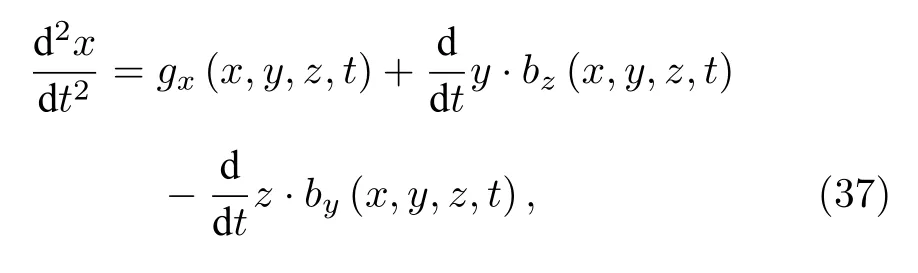
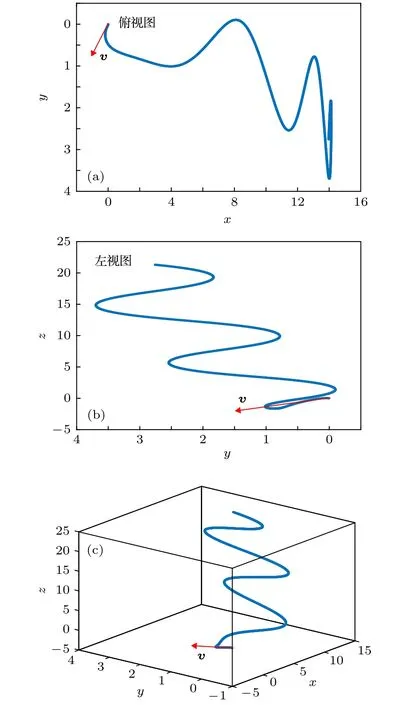
圖4 模式二下測(cè)試粒子的運(yùn)動(dòng)軌跡 (a) 測(cè)試粒子在余弦時(shí)變引力磁場(chǎng)中運(yùn)動(dòng)軌跡的俯視圖;(b) 測(cè)試粒子在余弦時(shí)變引力磁場(chǎng)中運(yùn)動(dòng)軌跡的左視圖;(c) 測(cè)試粒子在余弦時(shí)變引力磁場(chǎng)中的全空間運(yùn)動(dòng)軌跡Fig.4.The test-particle's track in cosine time-varying GM field: (a) The top view of the test-particle's track;(b) the left view of the test-particle's track;(c) the test-particle's track in the whole space.

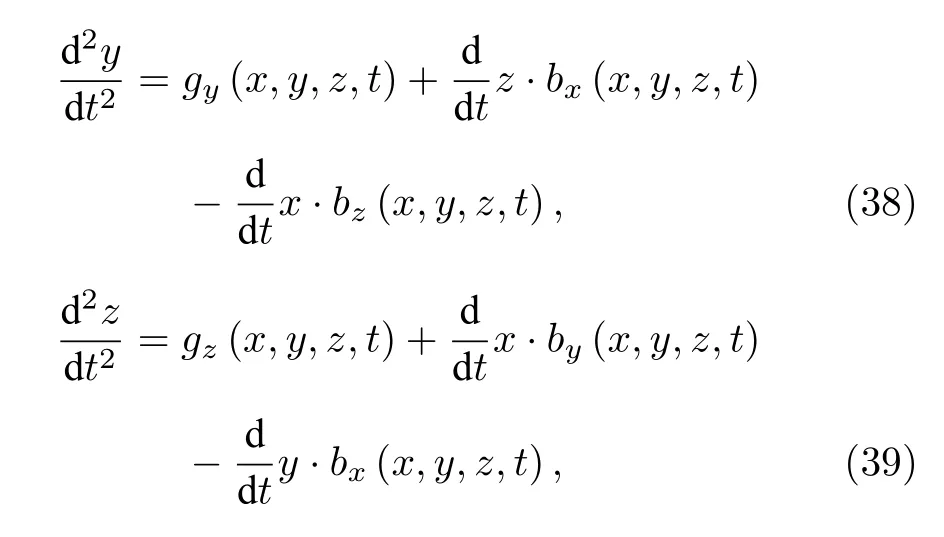
保持引力電場(chǎng)g的空間分量 ,及 全部為零的前提下,令引力磁場(chǎng)b的x分量發(fā)生下列兩種模式的時(shí)變,它們分別對(duì)應(yīng)于引力磁場(chǎng)的線性時(shí)變和余弦時(shí)變,與此同時(shí)令引力磁場(chǎng)b的y分量在空間上進(jìn)行非周期變化,即

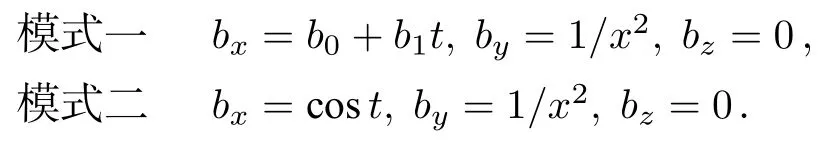
根據(jù)(37)式—(39)式的微分方程,可以借助仿真軟件繪制測(cè)試粒子在兩種模式下的運(yùn)動(dòng)軌跡,如圖3及圖4所示.

4.2 引力感應(yīng)效應(yīng)和引力拖曳效應(yīng)

在第2節(jié)中,通過定義引力場(chǎng)的廣義標(biāo)勢(shì)和廣義矢勢(shì)并采用洛倫茲規(guī)范條件得到了描述弱引力場(chǎng)運(yùn)動(dòng)的引力場(chǎng) Maxwell方程.在方程中,(8b)式所描述的物理學(xué)規(guī)律對(duì)應(yīng)了電動(dòng)力學(xué)的法拉第電磁感應(yīng)定律,它表示在弱引力場(chǎng)中時(shí)變的引力磁場(chǎng)能夠在空間激發(fā)感應(yīng)引力電場(chǎng)(即感生牛頓引力場(chǎng)),因此將(8b)式所描述的物理學(xué)規(guī)律稱作引力感應(yīng) (gravitational induction)效應(yīng).引力感應(yīng)效應(yīng)來源于線性愛因斯坦方程,它是線性引力論的一個(gè)特有現(xiàn)象,這也是線性引力理論區(qū)別于經(jīng)典引力論的一個(gè)動(dòng)力學(xué)特征.

引力感應(yīng)現(xiàn)象的研究起步于20世紀(jì)70年代.實(shí)驗(yàn)方面,最早由Braginsky等[31]針對(duì)引力感應(yīng)效應(yīng)設(shè)計(jì)了一系列有效的驗(yàn)證實(shí)驗(yàn),這些實(shí)驗(yàn)裝置的設(shè)計(jì)原理以法拉第電磁感應(yīng)定律為理論參考且結(jié)構(gòu)十分精巧,均能在實(shí)驗(yàn)室中得以實(shí)現(xiàn).后期由Tajmar等[8]進(jìn)行了液氦低溫超導(dǎo)鈮環(huán)旋轉(zhuǎn)實(shí)驗(yàn),有力地驗(yàn)證了引力感應(yīng)現(xiàn)象的真實(shí)性;理論方面,由Tajmar和Assis[3]建立了一類旋轉(zhuǎn)球殼模型來研究引力感應(yīng)效應(yīng),如圖5所示,模型由靜止內(nèi)環(huán)和旋轉(zhuǎn)外球殼兩部分組成.該研究的基本思路是,外部球殼在外界驅(qū)動(dòng)下旋轉(zhuǎn)角速度?發(fā)生時(shí)變將會(huì)激發(fā)時(shí)變引力磁場(chǎng),時(shí)變引力磁場(chǎng)在靜止內(nèi)環(huán)的平面產(chǎn)生感應(yīng)引力電場(chǎng),此時(shí)就會(huì)有一個(gè)方位角力作用在內(nèi)環(huán)的每個(gè)元素上,內(nèi)環(huán)因此將產(chǎn)生方位加速度開始旋轉(zhuǎn).Tajmar等根據(jù)旋轉(zhuǎn)球殼模型給出了引力感應(yīng)的表達(dá)式,但限于球殼模型的復(fù)雜性,文中未能利用電動(dòng)力學(xué)的分析方法通過旋轉(zhuǎn)球殼模型來展示引力感應(yīng)的過程.因此,為了更加清晰地向讀者展示引力感應(yīng)的過程,本節(jié)將通過一種簡(jiǎn)單的雙層微管模型來研究引力感應(yīng)效應(yīng).

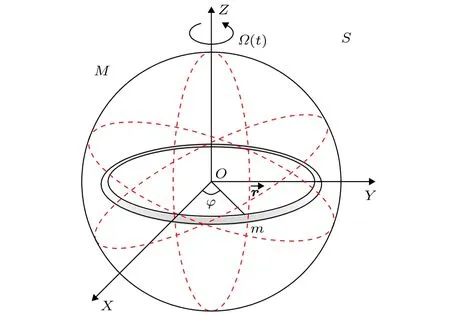
圖5 用于研究引力感應(yīng)效應(yīng)的旋轉(zhuǎn)球殼模型Fig.5.The rotating spherical shell model for studying the gravitational induction effect.

我們建立了如圖6所示的引力感應(yīng)演示模型,模型中1環(huán)的作用是為2環(huán)提供時(shí)變的引力磁場(chǎng),1環(huán)中由B端向管內(nèi)流入一種均勻流體并從A端流出,2環(huán)中則填充相同且靜止的均勻流體.由于1環(huán)要產(chǎn)生時(shí)變的引力磁場(chǎng),所以管內(nèi)流體的角動(dòng)量應(yīng)當(dāng)是時(shí)變(含時(shí))的.

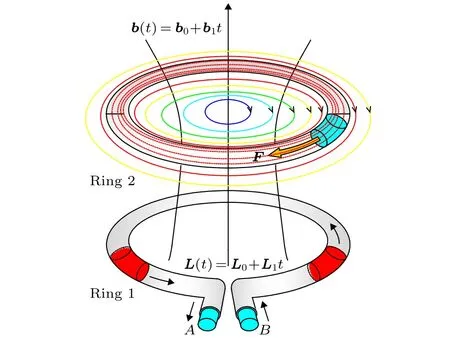
圖6 基于微管模型的引力感應(yīng)演示模型Fig.6.The demonstration model for studying gravitational induction based on the microtube model.

如圖7(a)所示,設(shè)定流體的含時(shí)角動(dòng)量為[11]

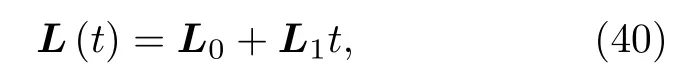
其中,L0為 1 環(huán)中流體的初始 (固有)角動(dòng)量,L1為流體含時(shí)角動(dòng)量的增長(zhǎng)率.將 (40)式代入(21)式中,則由1環(huán)所提供的時(shí)變引力磁場(chǎng)在2環(huán)中的引力磁矢勢(shì)為[11]那么通過2環(huán)的時(shí)變引力磁通量可借助引力磁矢勢(shì)表示為

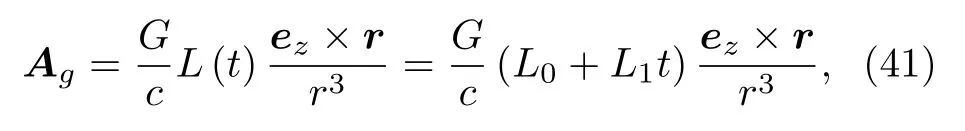
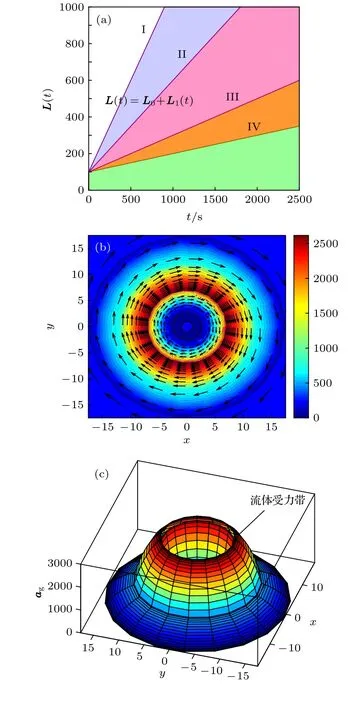
圖7 流體參數(shù)設(shè)定及渦旋場(chǎng)的仿真 (a) 流體含時(shí)角動(dòng)量的線性函數(shù);(b) 環(huán)2所在平面內(nèi)激發(fā)的渦旋引力電場(chǎng)的強(qiáng)度色譜圖;(c) 環(huán)2內(nèi)流體的受力區(qū)域Fig.7.The parameter description of fluid and the vortex field’s simulation: (a) The linear function between the angular momentum L and time;(b) the distribution of vortex field in the z=0 plane which produced by the ring 2;(c)the fluid’s stressed region in the plane of the ring 2.

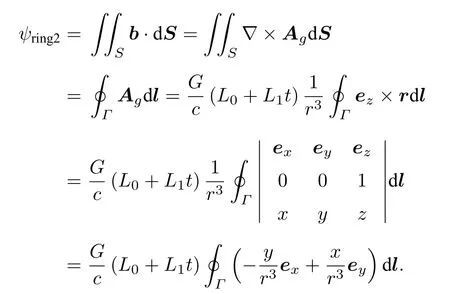
采用直角坐標(biāo)系表示引力磁矢勢(shì)的各分量,即

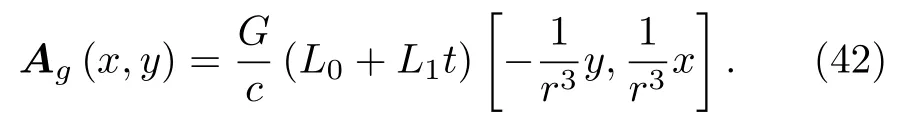
則根據(jù)第二類曲線積分的求解方法,時(shí)變引力磁通量表示為

代 入 2環(huán)z=0 平 面 的 參 數(shù) 方 程x=r2cosθ,y=r2sinθ,有

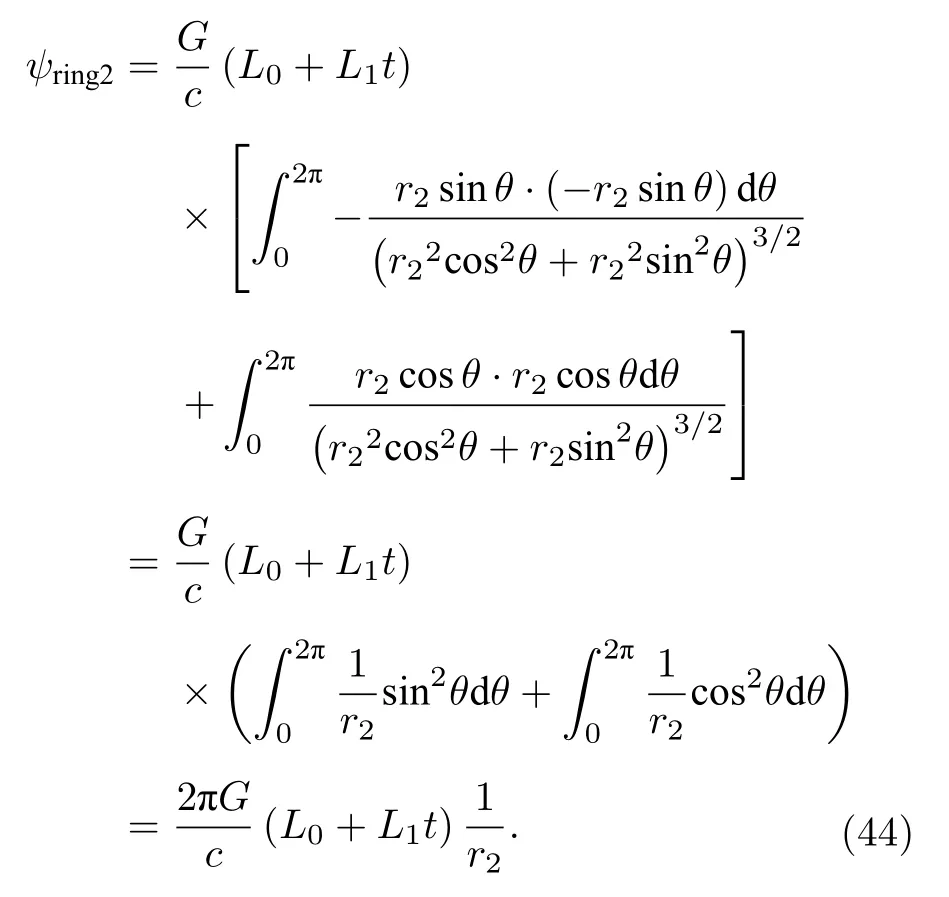
對(duì)于2環(huán),由于1環(huán)向其提供了時(shí)變引力磁場(chǎng),那么2環(huán)的引力磁通量也相應(yīng)發(fā)生時(shí)變,根據(jù)引力感應(yīng)效應(yīng)此時(shí)在2環(huán)所在的平面內(nèi)會(huì)激發(fā)出渦旋引力電場(chǎng),強(qiáng)度及分布情況如圖7(b)所示.由于2環(huán)的管腔內(nèi)也填充了相同且靜止的均勻流體,那么受渦旋引力電場(chǎng)的作用流體將在2環(huán)管腔內(nèi)發(fā)生定向流動(dòng).類似地,把這種在一次回路中因質(zhì)荷加速運(yùn)動(dòng)(產(chǎn)生加速質(zhì)量流)而在二次回路中產(chǎn)生力的牽引作用的現(xiàn)象普遍稱作引力電磁理論背景下的引力拖曳(Gravitational dragging)現(xiàn)象或慣性系拖曳現(xiàn)象[3].

本模型中,在引力感應(yīng)效應(yīng)下2環(huán)中的均勻流體的每一個(gè)單位元素都會(huì)得到一個(gè)方位加速度,其在大小和方向上對(duì)應(yīng)了渦旋引力電場(chǎng),而在電動(dòng)力學(xué)中可以證明感生電場(chǎng)作為一種橫場(chǎng)是矢勢(shì)Ag的負(fù)時(shí)間微商[32],所以2環(huán)流體具有的這個(gè)方位加速度表示為

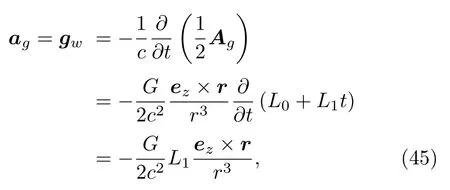
其中,gw表示渦旋引力電場(chǎng).那么渦旋引力電場(chǎng)在2環(huán)的閉合環(huán)路上產(chǎn)生的引力電動(dòng)勢(shì)表示為

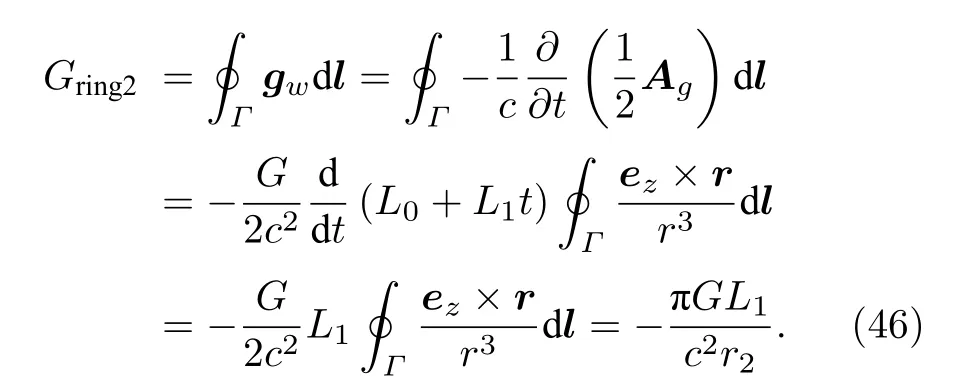
此時(shí),通過(44)式與(46)式能夠得到引力電動(dòng)勢(shì)G與引力磁通量ψ之間的關(guān)聯(lián)如下

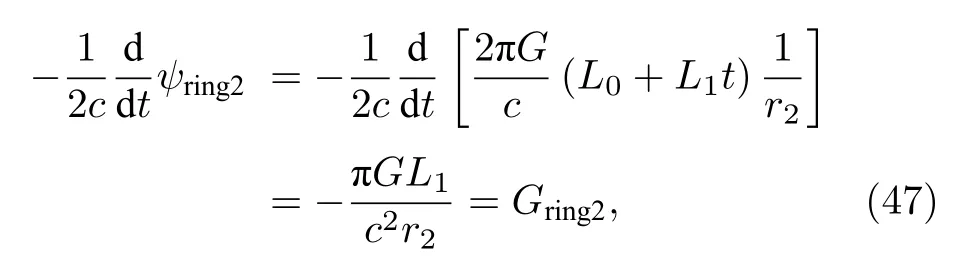
其通式表示為:

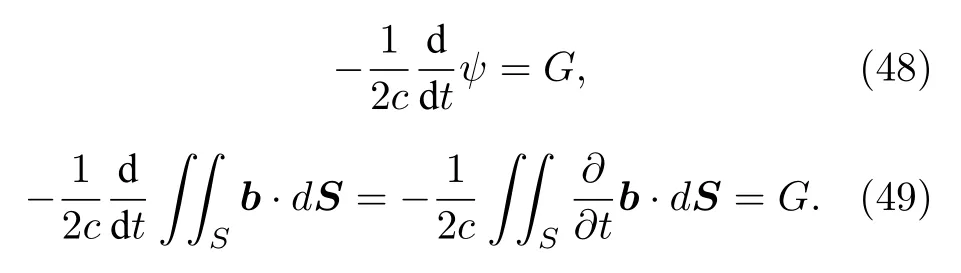
那么(48)式及(49)式所示的這種關(guān)聯(lián)性正是法拉第電磁感應(yīng)定律在引力場(chǎng)中的體現(xiàn),它們與(8b)式合起來是引力感應(yīng)效應(yīng)的特征表述.可以看到弱引力場(chǎng)中的引力感應(yīng)效應(yīng)與法拉第電磁感應(yīng)定律在形式上很相似,但仍然差一個(gè)1/2c因子,這本質(zhì)上是由于廣義引力標(biāo)勢(shì)、廣義引力矢勢(shì)與電磁標(biāo)勢(shì)、電磁矢勢(shì)在表示形式上的差別.

4.3 引力感應(yīng)、引力拖曳效應(yīng)的意義及展望

如本文 2.2 節(jié)中的介紹,Tajmar與 de Matos進(jìn)行過一個(gè)與圖6所示模型原理相近的實(shí)驗(yàn),目的是驗(yàn)證旋轉(zhuǎn)超導(dǎo)鈮環(huán)是否可以產(chǎn)生比常溫非超導(dǎo)環(huán)境下更強(qiáng)的引力磁場(chǎng).根據(jù)本文4.2節(jié)中的解釋,加速旋轉(zhuǎn)的鈮環(huán)作為一次回路會(huì)向全空間激發(fā)時(shí)變引力磁場(chǎng),而在加速度計(jì)所在的二次回路中由于引力感應(yīng)效應(yīng)會(huì)產(chǎn)生渦旋引力電場(chǎng)(感應(yīng)引力電場(chǎng)),受渦旋引力電場(chǎng)的作用加速度計(jì)將受到拖曳力并產(chǎn)生計(jì)數(shù).最終實(shí)驗(yàn)結(jié)果與理論預(yù)期一致,加速度計(jì)受到了強(qiáng)烈的拖曳力,檢測(cè)到的加速度場(chǎng)的平均值是噪聲(干擾信號(hào))的3.3倍以上,這表明de Matos的理論是正確的,即低溫超導(dǎo)環(huán)境下的鈮環(huán)能夠產(chǎn)生比常溫環(huán)境下更強(qiáng)的引力磁場(chǎng).此外,我們分析認(rèn)為該實(shí)驗(yàn)還有兩個(gè)十分重要的結(jié)論:

1)首次在地面實(shí)驗(yàn)室中記錄到了具備可測(cè)量性的引力磁場(chǎng),同時(shí)也驗(yàn)證了線性引力理論及引力電磁理論(GEM)的正確性;

2)充分驗(yàn)證了引力感應(yīng)現(xiàn)象及慣性系拖曳現(xiàn)象的真實(shí)性.

Everitt指出Tajmar等的實(shí)驗(yàn)結(jié)果有望成為一些新技術(shù)的基礎(chǔ)[21],應(yīng)用低溫超導(dǎo)技術(shù)人們可以通過改變超導(dǎo)體的旋轉(zhuǎn)加速度及旋轉(zhuǎn)方向來設(shè)計(jì)一系列基于引力感應(yīng)和引力拖曳效應(yīng)的引力磁場(chǎng)激發(fā)裝置,這些裝置理論上能夠在空間任意方向上產(chǎn)生人們所需的拖曳力,從而有可能實(shí)現(xiàn)對(duì)任意物體的推動(dòng)和懸浮,還可用于制造零重力環(huán)境.此外,除了低溫超導(dǎo)鈮環(huán)實(shí)驗(yàn),Tajmar和 de Matos[27]還推薦利用超流體(例如液態(tài)氦)代替旋轉(zhuǎn)鈮環(huán)重復(fù)他們的實(shí)驗(yàn),力求得到更為顯著的實(shí)驗(yàn)效果.理論上,本文認(rèn)為后期可以按照?qǐng)D6所示的模型加工類似的環(huán)狀微管,并通入勻加速流動(dòng)的液態(tài)氦(或其他超流體)完成超流體引力磁場(chǎng)激發(fā)裝置的測(cè)試,進(jìn)一步驗(yàn)證 Tajmar,de Matos等人的理論,同時(shí)本文期望能夠以該模型為基礎(chǔ)進(jìn)一步在工程上實(shí)現(xiàn)引力感應(yīng)及引力拖曳效應(yīng)的應(yīng)用,為實(shí)際應(yīng)用中提供全新的、通用的動(dòng)力.

至此,我們?cè)诘?節(jié)中研究了通有勻速流體的環(huán)狀微管模型的引力磁場(chǎng)遠(yuǎn)場(chǎng)分布特征,在第4節(jié)中研究了引力磁場(chǎng)對(duì)應(yīng)的動(dòng)力學(xué)效應(yīng),首次對(duì)測(cè)試粒子在時(shí)變引力磁場(chǎng)中的運(yùn)動(dòng)軌跡進(jìn)行了研究,最主要地,利用結(jié)構(gòu)相對(duì)簡(jiǎn)單的雙層微管模型模擬了引力感應(yīng)效應(yīng)的全過程,并定量計(jì)算和驗(yàn)證了引力感應(yīng)效應(yīng),解釋了慣性系拖曳現(xiàn)象.綜上,本文希望利用這種簡(jiǎn)單的物理模型為今后引力磁場(chǎng)及其連帶效應(yīng)的相關(guān)研究帶來一些新的方法和思路.

5 結(jié) 論

本文基于線性引力理論從引力場(chǎng)的場(chǎng)量中分解出了引力的磁分量并定義了引力磁場(chǎng);進(jìn)一步建立了一種通有勻速流體的環(huán)狀微管模型,研究了引力磁場(chǎng)在全空間的分布模式;然后建立了一種新的雙層結(jié)構(gòu)微管模型,研究了時(shí)變引力磁場(chǎng)中的引力感應(yīng)效應(yīng)和其產(chǎn)生的慣性系拖曳效應(yīng).通過數(shù)值計(jì)算以及仿真結(jié)果可以表明,這種由通有勻速流體的微管產(chǎn)生的靜引力磁場(chǎng)的遠(yuǎn)場(chǎng)分布模式與磁偶極子磁場(chǎng)的遠(yuǎn)場(chǎng)分布模式十分類似,二者呈現(xiàn)出了明確的類比關(guān)系;在引力磁場(chǎng)的動(dòng)力學(xué)效應(yīng)方面,本文選取了線性時(shí)變和余弦時(shí)變這兩種基本的時(shí)變模式研究了時(shí)變引力磁場(chǎng)中運(yùn)動(dòng)粒子的軌跡.仿真結(jié)果表明,在線性時(shí)變模式下測(cè)試粒子的運(yùn)動(dòng)軌跡是一條螺旋半徑隨時(shí)間改變的螺旋線,在余弦時(shí)變模式下測(cè)試粒子的運(yùn)動(dòng)軌跡是一類隨時(shí)間規(guī)律變化的振蕩曲線.而通過建立一種雙層結(jié)構(gòu)的微管模型,本文改進(jìn)了前人對(duì)引力感應(yīng)效應(yīng)的研究方法,利用這種簡(jiǎn)單的物理模型對(duì)引力感應(yīng)的全過程進(jìn)行了完整的理論驗(yàn)證,并依據(jù)引力感應(yīng)效應(yīng)解釋了廣義相對(duì)論中成因復(fù)雜的慣性系拖曳現(xiàn)象.從物理與工程的角度來看,本文所建立的模型以及提出的研究手段有望成為一些新工程技術(shù)的理論基礎(chǔ),例如借助引力感應(yīng)模型原則上可以加工制作一種通有超流體的環(huán)狀微管從而在空間各個(gè)方向上形成可調(diào)控的拖曳力,進(jìn)一步利用疊加原理在工程上產(chǎn)生實(shí)際應(yīng)用中所需的任意方向、任意強(qiáng)度的通用動(dòng)力.