高溫作業專用服裝溫度變化的數學原理及其應用

盧 鵬，徐昌貴

（西南交通大學數學學院，四川成都610031）

人們在高溫環境下工作時，需要穿著專用服裝以免灼傷.專用服裝由三層織物材料構成，即I、II、III層，其中I 層與外界環境接觸，III 層與皮膚之間還存在空隙，記為IV 層.在設計專用服裝時，為了降低研發成本、縮短研發周期，將體內溫度控制在37°C 的假人放置在實驗室的高溫環境中，測量假人皮膚外側的溫度. 專用服裝材料的一些參數值如表1 所示.對環境溫度為75 °C，工作時間為90 分鐘的情形開展實驗，測量得到假人皮膚外側的溫度（見表2，完成數據可查文獻[1]）. 本文首先對環境―人體―服裝傳熱的物理過程進行推理和分析，綜合傳熱學知識[2-3]將服裝導熱過程簡化為一維平板熱傳導模式，接著用微元法[4]推導出一維熱傳導偏微分方程，然后從材料的均勻性得到了不同材料在分界面處溫度連續、熱量連續等條件，并根據實驗要求確定初始條件和邊值條件，由此建立了在穩定環境中專用服裝熱傳導的偏微分方程組模型. 通過對模型進行求解[5-7]，得出每層傳播的規律. 最后對結果進行了驗證，以期可用于指導服裝的生產與研制.

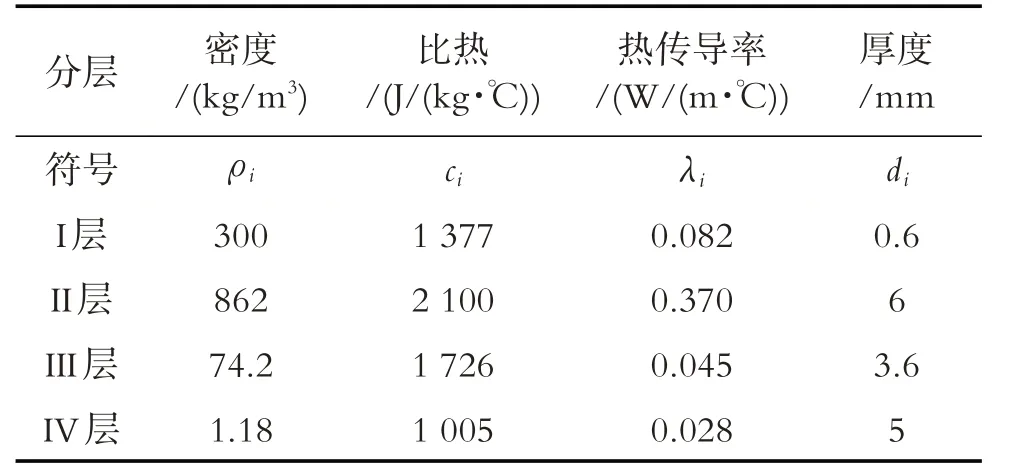
表1 專用服裝材料的參數值

表2 假人皮膚外側的測量溫度

1 問題分析

1.1 一維化思想的分析

由于熱量在傳遞過程中，最終熱量的對外表現形式為溫度場函數T(x,y,z,t)，而在本文中，高溫防護服裝材料的各處均在進行熱量的傳導，對任意一個熱量微元，由于材料各向分布均勻，即各個熱元傳熱的速度是互相協調的，因此微元在垂直向的熱量變化是相同的，即在圖1 中Y方向上溫度處處相同，由此可以認為熱量是沿一個方向傳遞，熱元的側面之間沒有進行熱量交換，即二維溫度分布可進一步表示為T(x,t)，即溫度為時間和單維度位置變量的函數.

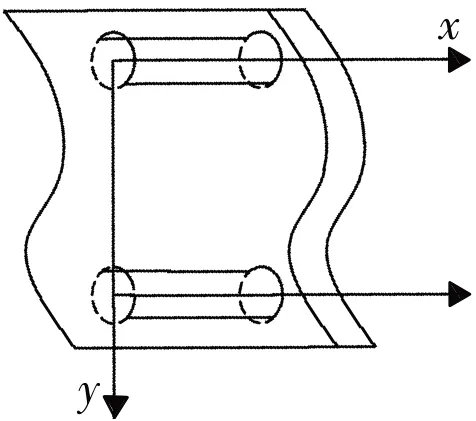
圖1 熱量微元的選取示意圖

1.2 一維熱傳導方程的推導

（1）熱量流動速率的確定

在對服裝材料上任意位置取一個某種材料的圓柱體微元，該材料微元的橫截面均勻且材質相同，熱量只能沿某特定方向進行流動，此處方向約定為x軸方向. 根據經驗原則，在某時刻t，通過點x橫截面上的單位面積熱流動速率為[8]：

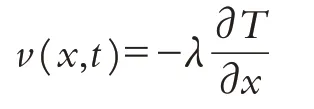
其中：λ為該材料的熱傳導率，v(x,t)為熱流速率.

圖2是熱量流入材料微元的示意圖.

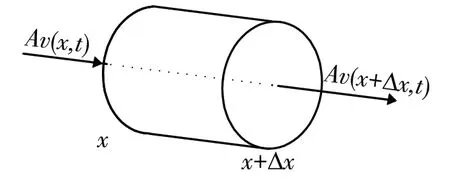
圖2 熱量流入材料微元的示意圖

由圖2可知，通過兩個端面的熱量流動速率為：

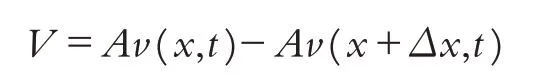
將v(x,t)代入得：

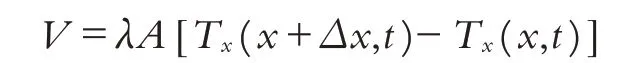
（2）單種材料微元吸收的熱量[9-10]

把該材料圓柱微元溫度從0 加熱到T所需的熱量為：

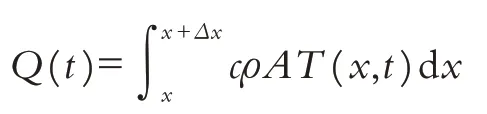
對上式兩邊進行微分并應用積分中值定理有：

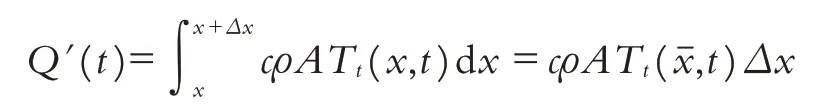
其中為x與x+Δx之間中的某個值.

（3）一維熱傳導方程的確定

Q(t)表示把圓柱微元對應于x與x+Δx的一小段溫度從0 度升到已知溫度T(x,t)所需的熱量，又因為熱流僅從端面進出，由此根據V=dQ/dt和熱量流動V表達式得：

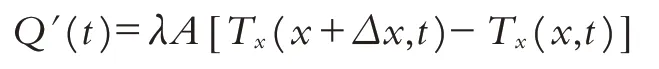
基于上述兩種不同的熱量速度推導方法得出的V相等，于是有：

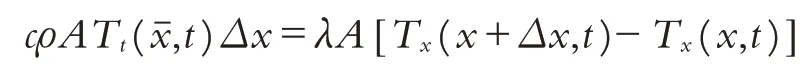
所以，可以得出

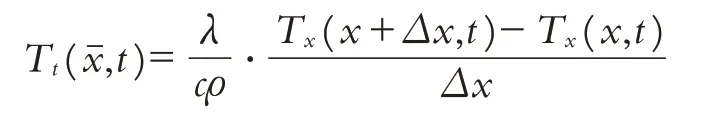
令Δx→0，即xˉ→x，可以得到熱量的一維傳導方程：

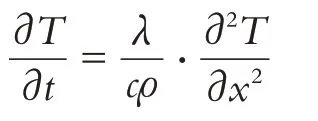
2 模型建立

2.1 坐標系建立及熱量傳遞機理分析

在忽略沿假人皮膚平面方向導熱的條件下，可把皮膚內的導熱問題認為是無限大平板問題，即一維導熱問題. 由題目可知，在高溫下工作的人體皮膚溫度必須在一定的范圍內，人體才能正常工作，而人體皮膚溫度升高是由于環境溫度向內傳遞，才不斷導致溫度越來越高，而高溫防護服的特點就在于能夠有效地減少熱量向人體傳遞，控制服裝內部的溫度，維持人體舒適溫度，而熱量向內傳遞是一個逐步傳遞過程，通過一層層防護服材料的過程.

建立如圖3 所示坐標系，根據前述分析，坐標系的兩個維度為材料的位置坐標和時間. 溫度分布是坐標位置和時間的二維函數，坐標軸的原點位置及熱量傳遞過程如圖3所示.

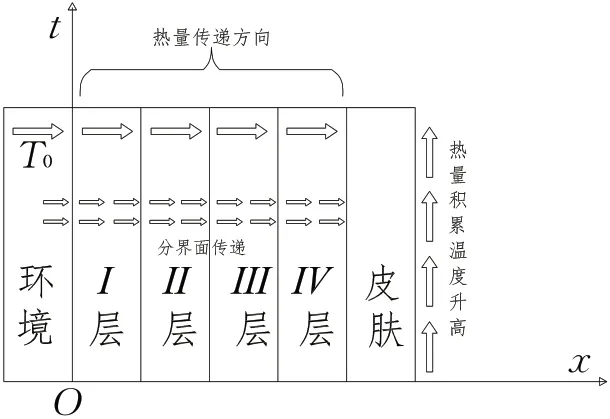
圖3 熱量傳遞過程示意圖

2.2 各織物材料層內一維熱傳導偏微分方程的建立

熱量在特定的某種材料中傳遞符合一維熱傳導規律，由此，建立任意層中熱量傳遞的偏微分方程.第i層織物材料中的一維熱傳導偏微分方程為：

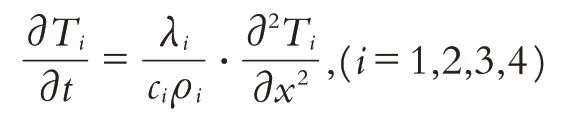
其中：Ti是第i層織物材料中的溫度場函數，為二元函數Ti(x,t)，x是織物材料在厚度方向的位置坐標.

2.3 各織物材料在分界面處傳導模式分析

能量在同種介質中按照一維熱傳導偏微分方程的遞變規律進行傳遞，根據熱量傳遞的連續性特征可知，溫度向下傳遞時，在分界面上二者的溫度應該相等，則有如下等式：

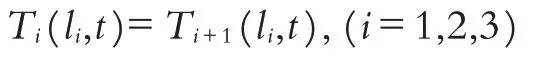
同時在交界面處熱流密度也是連續變化的，從而有如下等式：

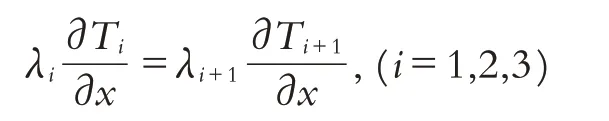
2.4 邊值條件的確定

由高溫防護服的工作環境可知，服裝最外層面料是直接暴露在空氣中的，最里層即第IV 層空隙與人體皮膚接觸，因此在溫度場函數中，當位置坐標確定后有如下邊界條件：

（ⅰ）織物材料層的左邊界條件：T1(0,t)=T0.

（ⅱ）織物材料層的右邊界條件：T4(l4,t)=T5.

其中：T0=75 ℃為外界環境的溫度；T5為人體皮膚外側溫度且數據由表2 給出；di表示第i層織物材料的厚度，li表示前i層織物材料的厚度和，即l4=d1+d2+d3+d4.

2.5 初值條件的確定

高溫防護服裝在進入實驗室之前，應該長期處于一個穩定環境場中，同時由于假人體內溫度一直控制為37 ℃，故有初值條件為：

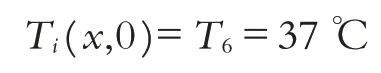
2.6 偏微分方程組模型的建立

基于上述熱量傳遞的分析過程以及相關的定解條件，可以建立起整個熱量傳導的正向偏微分方程組模型：

3 模型求解

在偏微分方程領域，這是一個一維拋物型方程，考慮到定解條件中既包含開始時刻織物材料層溫度分布的初始條件，又包含織物材料層溫度分布的邊值條件. 因此，這是一個一維熱傳導混合問題[11]. 由于混合問題的求解過程往往是比較復雜的，有時很難有解析解. 即使該一維熱傳導混合問題的解析解可以求出，其解的形式也通常是一個無窮級數形式，不易于對外界環境―服裝―人體整個系統熱量傳導及溫度變化過程進行分析. 因此，本文利用有限差分法對該偏微分方程組進行求解.

采用一定的網格劃分離散化溫度場，把實際連續的溫度場離散為有限數量的點. 用這些點上的溫度值近似描述連續的溫度場. 針對x-t平面，取Δx和Δt分別為x方向和t方向的步長，分別做一組平行于x軸和平行于t軸的直線，將x坐標等分為N份，將t坐標等分為M份. 則坐標可表示為(kΔx,jΔt)(k=1,2,…,N;j=1,2,…,M)的網格點，簡記為(k,j)，網格上每個格點對應一個溫度，則Ti(x,t)在此格點上的取值記為Ti(k,j)，如圖4所示.

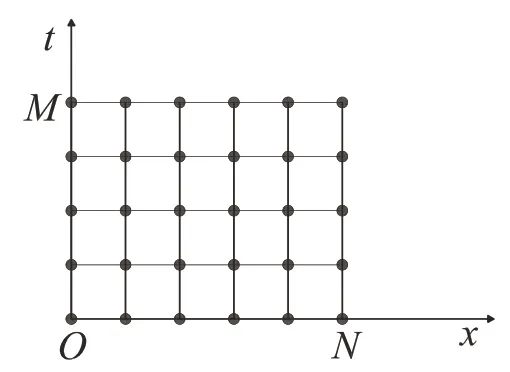
圖4 網格劃分示意圖

3.1 顯式差分算法

用二階中心差分近似代替溫度分布函數對空間的偏微分，即

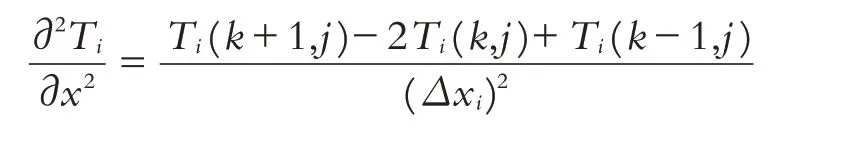
用向前差分近似代替溫度分布函數對時間的偏微分，即

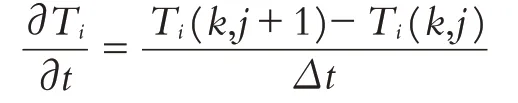
根據上述建立的差分格式，可將該偏微分方程改寫為：

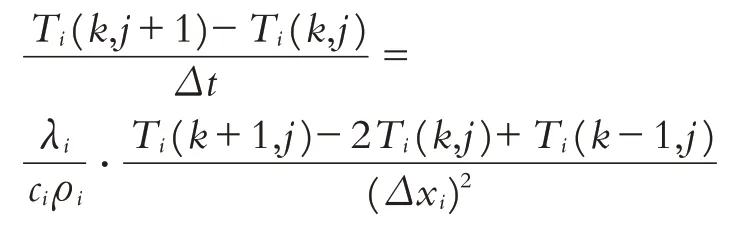
化簡為：

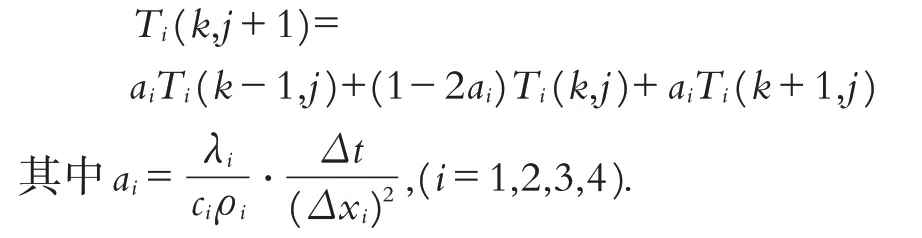
算法的計算過程是由Ti(k-1,j)、Ti(k,j)、Ti(k+1,j)三個點去計算Ti(k,j+1)，具體如圖5所示：

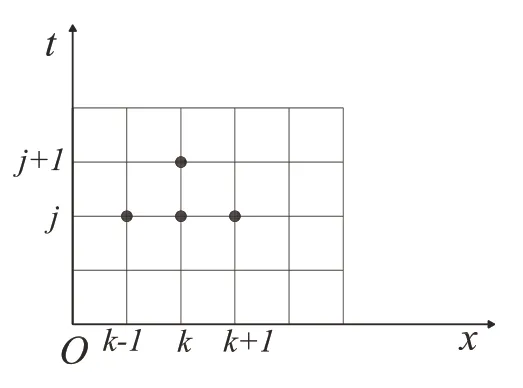
圖5 顯式差分格式

這樣根據上面公式，每次算完一行以后往上迭代就可以算出網格中所有點的值. 但需要注意是總共有四層，每層的ai取值不同；顯式方法在時，為數值穩定且收斂；所以在時間步長與位移步長取值時需要滿足條件；為了滿足收斂，每個部分的步長有可能不同；材料分界面上的網格節點(k,j)使用下面方程進行計算（溫度相等，熱量相等）：

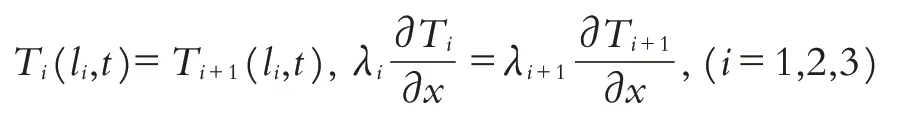
離散化第二個方程，化簡可得

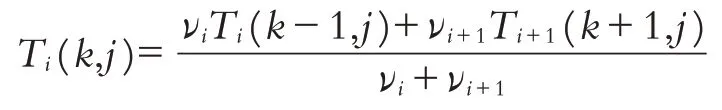
其中νi=λi/Δxi.

若要用顯式方式求解，時間步長要取為0.01 s，位移步長I、II、III層取為0.1 mm，IV 層取為1 mm，再按照上述公式計算可得結果.

3.2 隱式差分算法

用二階中心差分近似代替溫度分布函數對空間的偏微分，即

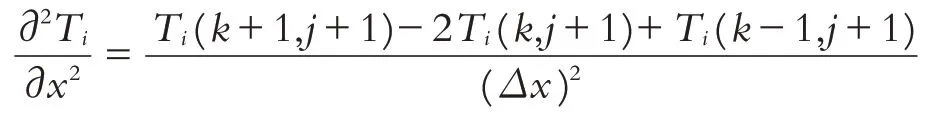
用向后差分近似代替溫度分布函數對時間的偏微分，即

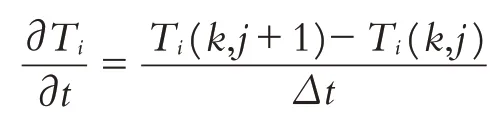
根據上述建立的差分格式，可將該偏微分方程改寫為：

化簡為：

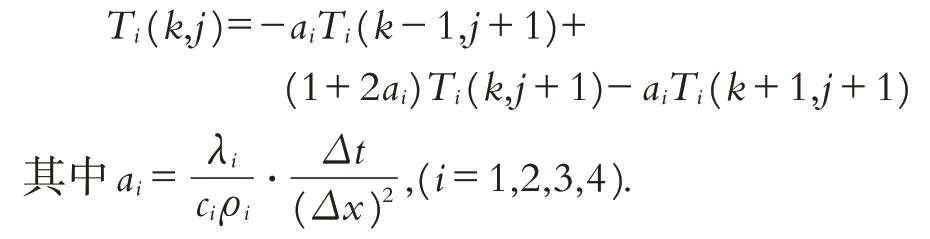
計算過程是由Ti(k-1,j+1)、Ti(k,j+1)、Ti(k+1,j+1)與Ti(k,j)建立一個線性方程組進行計算，具體如圖6所示：

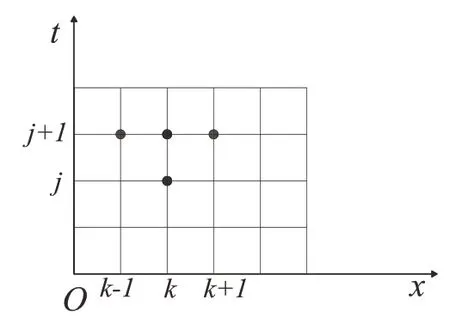
圖6 隱式差分格式

根據上面公式，每次求解一個聯立線性方程組后，再往上迭代就可以算出網格中所有點的值. 具體如下：

第一步：當j=0 時求解如下線性方程組，得出Ti(k,1)(i,=1,2,3,4;k=1,2,…,N-1)：

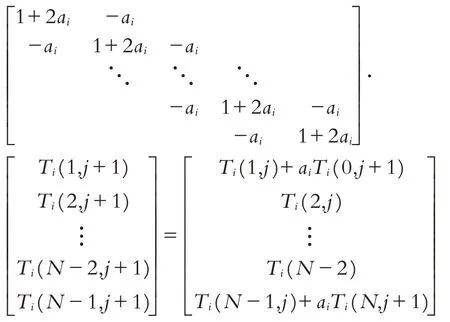
其中：

若規模較大的線性方程組直接采用高斯消元法求解，對于微型計算機來說運算量與存儲量難以承受，本文根據方程組系數矩陣的特點，采用追趕法（需要滿足一定條件，本題已滿足）求解，大大節省了計算時間.

第二步：當j=1,2,…,M-1 時求解M-1 個線性方程組，得出所有Ti.

需要注意的是總共有四層，每層的ai取值不同，在求解線性方程組時注意邊界條件；隱式方法不論ai的大小，都數值穩定且收斂，但計算量會較顯式方法要大，因為每前進一個時間間隔，就需要求解一個聯立的線性方程組；方法本身收斂，每個部分在取步長時可以相同，即Δx=Δxi；材料分界面上的網格節點(k,j)由下面方程給出：

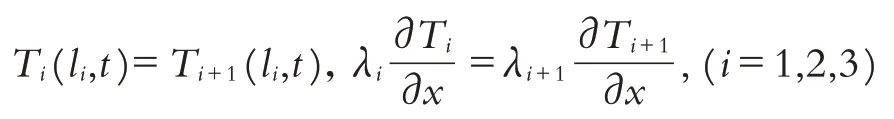
離散化第二個方程，化簡可得

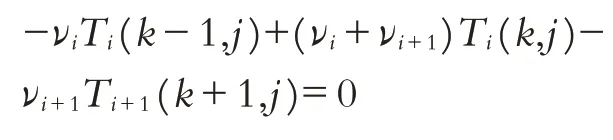
其中νi=λi/Δxi.

3.3 結果說明

為了計算方便及穩定，采用隱式差分算法進行計算，時間步長取為1 s，四層的位移步長都取為0.1 mm. MATLAB 軟件[12]編程計算偏微分方程組即可得到溫度分布數據表格（表3）.

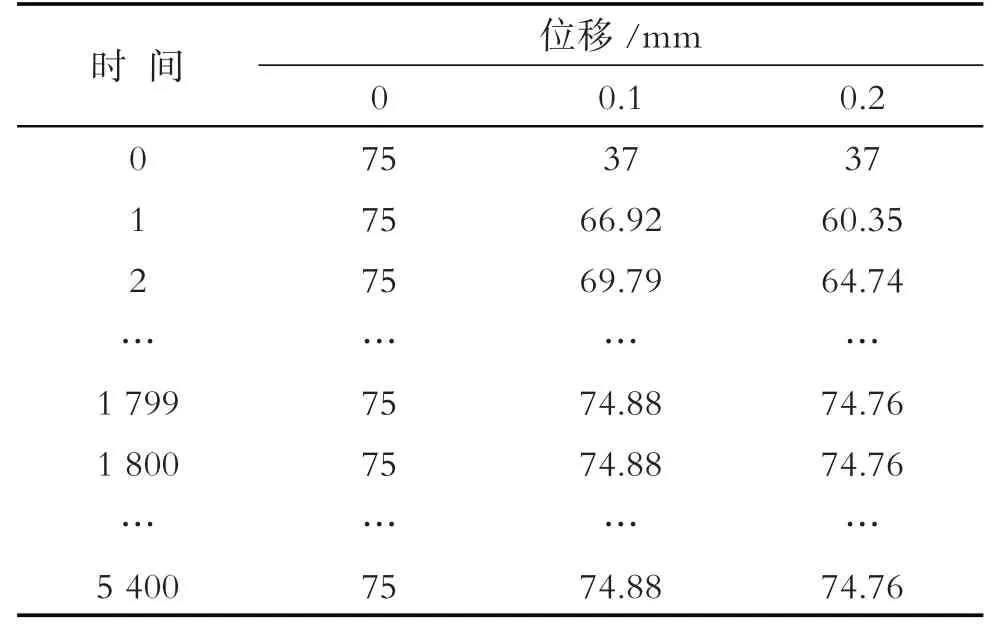
表3 部分溫度分布數據

溫度分布函數Ti(x,t)是時間參數t和空間參數x的二元函數，繪制溫度分布三維圖（圖7）.由圖7可見，初始時刻服裝材料各處溫度均為37 ℃. 假人進入實驗室高溫環境后，服裝材料溫度迅速上升，其中I層材料溫度變化幅度最大，因為其與外界環境直接接觸. 針對同一時間，隨著坐標位置的增加，節點處溫度上升幅度逐漸減小；針對同一節點，隨著時間增加，該節點處溫度逐漸上升，但溫度變化率逐漸降低，最后所有的節點溫度趨于某一穩定溫度值.

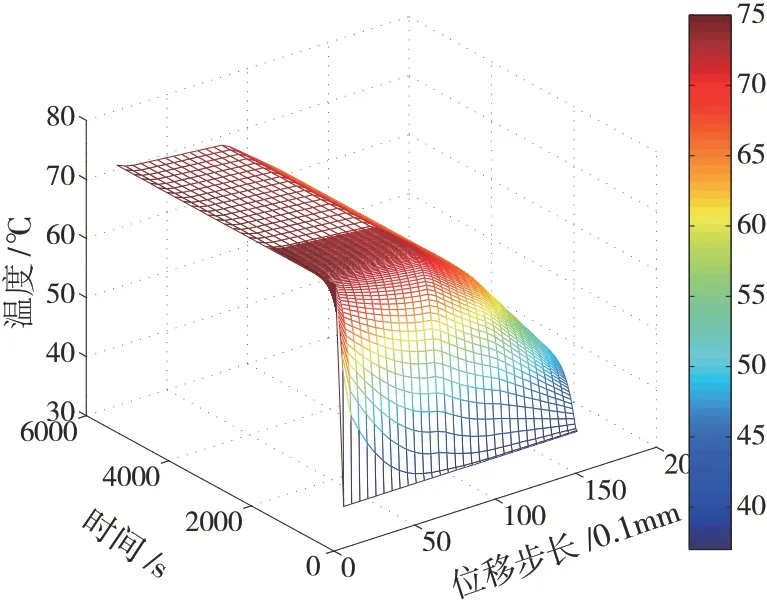
圖7 溫度分布三維圖

圖8 反映了不同時刻下織物材料內部溫度的變化. 由圖8 可以看出，隨著時間的增加，各個位置處網格節點的溫度在逐漸趨于穩定，即熱傳遞達到了穩定狀態；且在穩定狀態下，各個網格節點的溫度隨位置坐標呈線性變化.

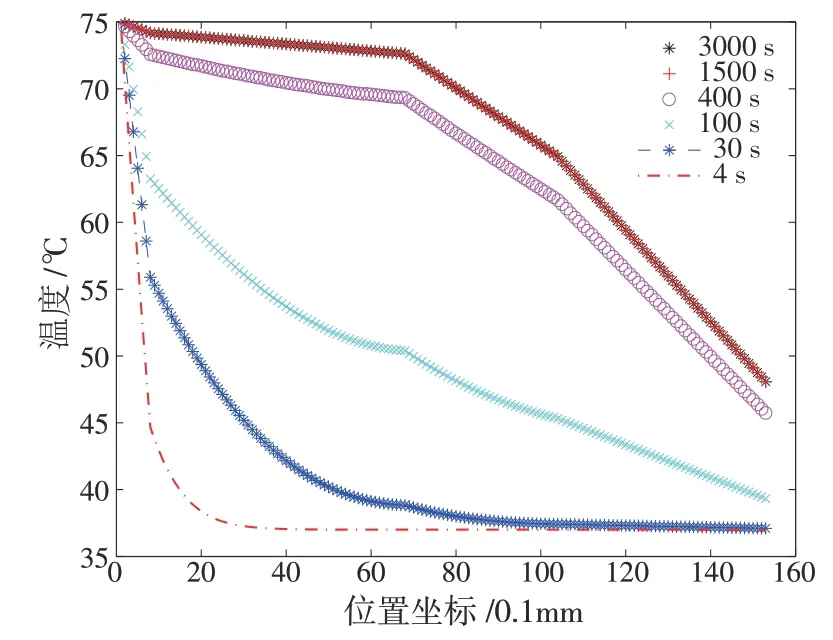
圖8 不同時刻下織物材料內部溫度的變化

圖9 的分界面處織物材料溫度隨時間的變化表明，位于分界處的網格節點，隨著時間的增加，這些節點上的溫度均有一個快速增長的過程，但在該過程中溫度變化的速率逐漸變緩，最后，節點上的溫度都達到了穩定狀態.

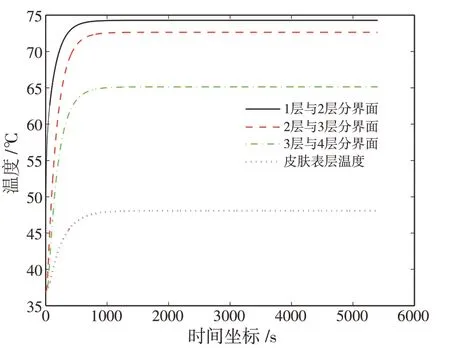
圖9 分界面處織物材料溫度隨時間的變化

4 模型驗證

由表2數據和圖9可以發現，當假人放入穩定的環境中，從1 645 s以后溫度的變化將趨于穩定，這個時候溫度和時間就沒有關系了，只和位移有關系.故可以建立穩定狀態下的數學模型，并用來檢驗非穩態模型所算出的結果.

穩定狀態下的數學模型如下：

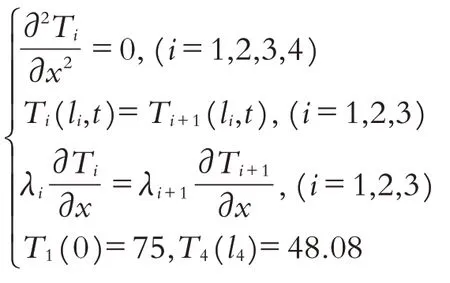
求解可得：

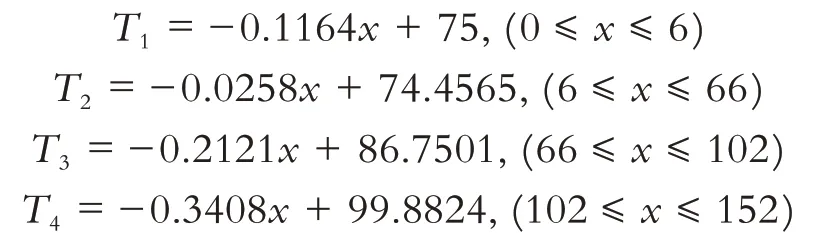
由原模型計算可知，當1 645 s后溫度趨于穩定，表4 給出了穩定狀態和原模型1 645 s后不同位置上的溫度，同時也給出了兩種結果的散點圖（圖10）.從表4 和圖10 可以看出，兩種方式的計算結果幾乎沒有差別，所以本文所建立的偏微分方程組模型以及求解的結果是正確的.

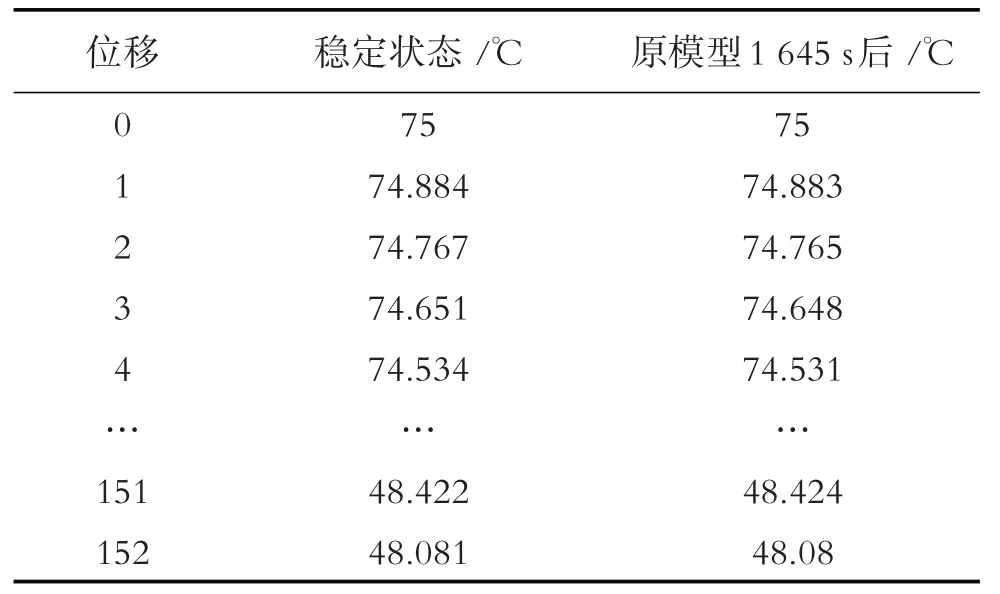
表4 兩種模型溫度結果對比

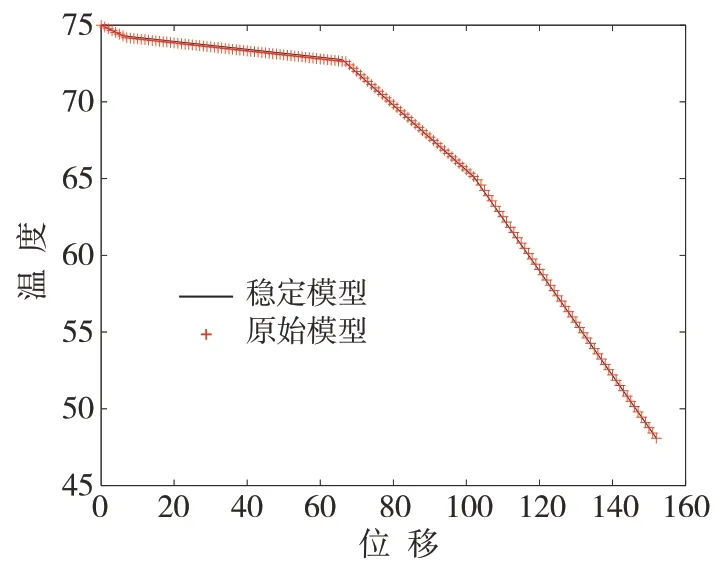
圖10 兩種模型的溫度變化曲線

5 結語

本文建立了在穩定環境中專用服裝熱傳導的偏微分方程組模型，由此可以掌握溫度變化的規律，同時改變材料中的某些參數值，運用模型和算法可得更多溫度變化的結果，對這些結果進行研究與分析，可以為生產專用服裝的科研人員提供參考，以使其降低研發成本，提高制作工藝.