圓錐曲線定值問題研究
2018-07-27 01:54:06廣西桂林市中山中學(xué)
數(shù)學(xué)大世界 2018年20期
廣西桂林市中山中學(xué) 秦 勇
本文通過對(duì)圓錐曲線定值問題的研究,總結(jié)歸納了解決圓錐曲線定值問題的主要策略。
一、參數(shù)法
幾乎所有的圓錐曲線定值問題都涉及參數(shù)的選取,必須通過參數(shù)作為中間量進(jìn)行計(jì)算,最后消去參數(shù),得到定值。
(1)求橢圓C的方程。
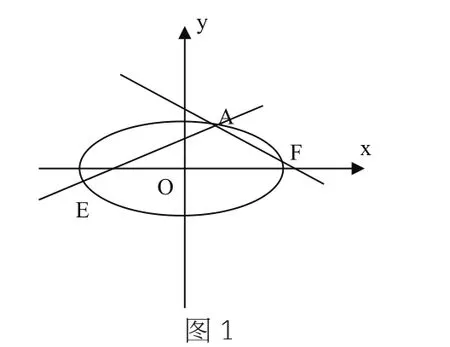
(2)E,F(xiàn)是橢圓C上的兩個(gè)動(dòng)點(diǎn),如果直線AE的斜率與AF的斜率互為相反數(shù),證明直線EF的斜率為定值,并求出這個(gè)定值。

(2)如圖1,設(shè)AE的斜率為k,則AF的斜率為-k。

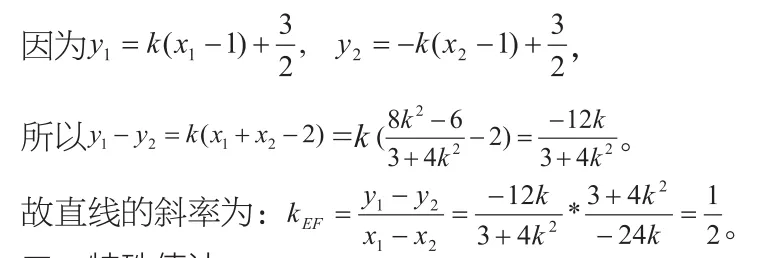
二、特殊值法
除了參數(shù)法之外,我們還可以用另一種方法求解定值問題,我們可以先在特殊情況下求出定值,然后我們?cè)僮C明定值與特殊情況無(wú)關(guān),在一般情況下也成立。
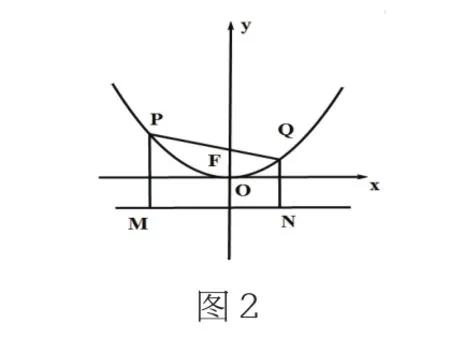
例2 過拋物線m:y=ax2(>0)的焦點(diǎn)F作直線l交拋物線于P、Q兩點(diǎn),若線段PF與FQ的長(zhǎng)分別為p,q,證明為定值。
證明:(1)在直線l與x軸平行的特殊情況下,有:

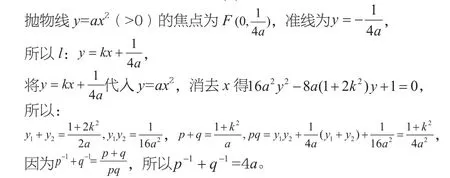
圓錐曲線定值問題是高中知識(shí)的一個(gè)難點(diǎn),在詳細(xì)研究了這類題型后,文中介紹了運(yùn)用參數(shù)和特殊到一般這兩種數(shù)學(xué)思想方法來解決圓錐曲線定值問題,希望能幫助讀者從總體上認(rèn)識(shí)圓錐曲線定值問題,增加在學(xué)習(xí)這部分知識(shí)時(shí)的信心,使我們?cè)诮鉀Q此類問題時(shí)很快地找到解題策略。
猜你喜歡
語(yǔ)數(shù)外學(xué)習(xí)·高中版上旬(2024年18期)2024-02-20 00:00:00
體育科技文獻(xiàn)通報(bào)(2022年3期)2022-05-23 13:46:54
中學(xué)生數(shù)理化(高中版.高二數(shù)學(xué))(2022年1期)2022-04-26 13:59:56
中學(xué)生數(shù)理化·中考版(2021年10期)2021-11-22 07:26:38
天津外國(guó)語(yǔ)大學(xué)學(xué)報(bào)(2021年3期)2021-08-13 08:32:18
遼金歷史與考古(2021年0期)2021-07-29 01:06:54
科技傳播(2019年22期)2020-01-14 03:06:54
中學(xué)生數(shù)理化·中考版(2019年10期)2019-11-25 09:39:04
民用飛機(jī)設(shè)計(jì)與研究(2019年4期)2019-05-21 07:21:24
汽車工程學(xué)報(bào)(2017年2期)2017-07-05 08:13:02

