齒輪測量中異常值的判定及剔除系統(tǒng)設(shè)計
時海濤,蘇智劍
(鄭州大學(xué) 機械工程學(xué)院,河南 鄭州450001)
0 引言
齒輪誤差的測量是一項要求十分嚴(yán)格的工作,測量數(shù)據(jù)的處理分析是齒輪誤差測量實驗的關(guān)鍵一環(huán),它直接關(guān)系著對齒輪制造精度以及齒輪測量裝置的穩(wěn)定性和可靠性的評價。在齒輪現(xiàn)場測量的過程中,由于測量環(huán)境的不穩(wěn)定、操作人員操作不當(dāng)?shù)纫蛩囟伎赡軙斐蓽y量時測量數(shù)據(jù)的突變,進而產(chǎn)生異常值,即粗大誤差[1]。測量數(shù)據(jù)的預(yù)處理是為了剔除由上述因素產(chǎn)生的粗大誤差,從而保證測量數(shù)據(jù)的科學(xué)性和準(zhǔn)確性[2]。
本文在對4種粗大誤差判定準(zhǔn)則分析研究的基礎(chǔ)上設(shè)計了粗大誤差判定系統(tǒng)[3],對齒輪測量數(shù)據(jù)進行異常值處理以保證測量數(shù)據(jù)的可靠性,以便對齒輪的誤差作出科學(xué)分析,為齒輪在裝配使用時預(yù)先做出裝配方案提供科學(xué)的依據(jù)。
1 測量數(shù)據(jù)異常值的判定方法
測量數(shù)據(jù)中的粗大誤差是一組測量數(shù)據(jù)出現(xiàn)的明顯脫離其他正常值的那些異常值,這些數(shù)值相差比較大,而且離散出現(xiàn)[4]。常用的判定準(zhǔn)則有狄克遜準(zhǔn)則、拉伊達準(zhǔn)則、格拉布斯準(zhǔn)則以及肖維勒準(zhǔn)則。在齒輪誤差測量的過程中,粗大誤差需要慎重處理,要結(jié)合其判定準(zhǔn)則作出科學(xué)的分析,綜合運用多種判定準(zhǔn)測處理異常值,以避免粗大誤差的遺漏和測量真值的誤判。
1.1 狄克遜判別法
狄克遜準(zhǔn)則是運用極差比法定義了4個統(tǒng)計量,根據(jù)測量數(shù)據(jù)量的不同分別采用不同的統(tǒng)計量。在計算統(tǒng)計量之前,需要先對測量數(shù)據(jù)進行從小到大的排序。有下面4個統(tǒng)計量:
(1)
當(dāng)3≤n≤7時,用統(tǒng)計量r10進行計算判別;當(dāng)8≤n≤10時,用統(tǒng)計量r11進行計算判別;當(dāng)11≤n≤13時,用統(tǒng)計量r21進行計算判別;當(dāng)14≤n≤15時用統(tǒng)計量r22進行計算判別。通過查詢臨界系數(shù)D(n,α)表,如果
rij>D(n,α)
(2)
那么判定xn或x1為粗大誤差值,否則為正常值。臨界系數(shù)D(n,α)存于excel表中;當(dāng)用狄克遜法判定時,判定系統(tǒng)直接從excel表中調(diào)用D(n,α)進行計算判別。其中n表示數(shù)據(jù)量,xn為第n個數(shù)據(jù),α為置信度,一般取置信度α為0.01。部分D(n,α)值如表1所示。

表1 部分狄克遜準(zhǔn)則臨界系數(shù)D(n,α)
1.2 拉伊達判別法
拉伊達準(zhǔn)則適用于測量數(shù)據(jù)量較大的情況,又稱為3σ準(zhǔn)則;當(dāng)數(shù)據(jù)量n≤10時,此方法無效[5]。設(shè)Xn為一組實驗數(shù)據(jù),Xi為可疑值,若要判斷出這組數(shù)據(jù)中的粗大誤差值,則需要先求出這組數(shù)據(jù)的算術(shù)平均值X及標(biāo)準(zhǔn)偏差σ,若
|Xi-X|>3σ
(3)
則判定Xi為粗大誤差,否則為正常值。
當(dāng)采用拉伊達準(zhǔn)則判定粗大誤差值時,每剔除一個粗大誤差值就需要重新計算剩余數(shù)據(jù)的算術(shù)平均值和標(biāo)準(zhǔn)偏差,依據(jù)判定準(zhǔn)則再次判定剩余數(shù)據(jù)中的粗大誤差,如此循環(huán)往復(fù)直至剔除全部誤差值。
1.3 肖維勒判別法
設(shè)Xn為一組實驗數(shù)據(jù),X為此組測量數(shù)據(jù)的算術(shù)平均值,σ為其標(biāo)準(zhǔn)偏差,k為肖維勒系數(shù),Xi為可疑值;若
|Xi-X|>σ>k
(4)
則判定Xi為粗大誤差值,否則為正常值。剔除粗大誤差值后,重新計算剩余數(shù)據(jù)的平均值和標(biāo)準(zhǔn)偏差,依次用判別法判別粗大誤差,如此循環(huán)直至剔除全部誤差。其中肖維勒系數(shù)存于excel表中。
1.4 格拉布斯判別法
格拉布斯判別法通常適用于小樣本容量的情況,在用格拉布斯判別法判定粗大誤差值之前,要先將測量數(shù)據(jù)按從小到大的順序排列[6],然后構(gòu)造統(tǒng)計量G1和Gn,并與相應(yīng)置信度α的統(tǒng)計臨界系數(shù)G(α,n)的值進行比較,最終判斷出粗大誤差值;當(dāng)判斷出粗大誤差值后,把剩余數(shù)據(jù)按以上方法重復(fù)進行判別,直至剔除所有粗大誤差值,具體方法如下:
G1=(X-X1)/σ,Gn=(Xn-X)/σ
(5)
當(dāng)G1≥Gn且G1>G時,則X1為粗大誤差值;當(dāng)Gn≥G1且Gn>G0時,則Xn為粗大誤差值;當(dāng)G1 表2 部分格拉布斯統(tǒng)計臨界系數(shù)G(α,n) 本文在對4種粗大誤差判定準(zhǔn)則分析的基礎(chǔ)上,基于VB6.0開發(fā)設(shè)計了齒輪測量異常值剔除系統(tǒng);該系統(tǒng)能夠在齒輪測量時,對由于操作人員操作不當(dāng)或其他外界突發(fā)等狀況而引起的測量異常值進行及時發(fā)現(xiàn)和剔除[7],以便對齒輪的某項數(shù)據(jù)進行重新精確的測量或補償[8]。 齒輪測量粗大誤差剔除系統(tǒng)主要有數(shù)據(jù)讀入、誤差剔除、數(shù)據(jù)查詢、保存、刷新、幫助幾個部分組成,系統(tǒng)界面如圖1所示。 圖1 齒輪測量異常值剔除系統(tǒng)界面 1) 數(shù)據(jù)輸入、輸出模塊 原始測量數(shù)據(jù)的讀入以及處理后數(shù)據(jù)的輸出、保存都采用I/O接口模塊來實現(xiàn)。在實際測量過程中,齒輪測量數(shù)據(jù)量是比較大的,如果用人工輸入的方式則會浪費大量的時間,嚴(yán)重降低測量工作的效率,所以本文采用文本格式 (*.txt)的方式進行數(shù)據(jù)的讀入及輸出,大大地提高了數(shù)據(jù)處理的效率。 2) 誤差剔除模塊 誤差剔除模塊由拉伊達、格拉布斯、狄克遜、肖維勒4個判別子模塊組成,在進行誤差剔除時點擊相應(yīng)菜單下的判別法進行數(shù)據(jù)判別的處理。 3) 數(shù)據(jù)庫訪問模塊 本系統(tǒng)除了拉伊達判別法外,其他3種判別法在進行粗大誤差判定時,依據(jù)測量數(shù)據(jù)量的不同都要重復(fù)調(diào)用相應(yīng)的判據(jù)系數(shù),所以本文運用數(shù)據(jù)庫訪問技術(shù),即ADO技術(shù),對判據(jù)系數(shù)excel數(shù)據(jù)庫表進行訪問[9],從而大大提高了數(shù)據(jù)處理的效率。以下為部分excel數(shù)據(jù)庫訪問程序代碼: Public Sub shujuku_Click() Dim cn As New ADODB.Connection Dim rs As New ADODB.Recordset cn.ConnectionString="Provider=Microsoft.Jet .OLEDB.4.0;PersistSecurityInfo=false; DataSource="&App.Path&""&"formshujuk u.xls;Extended Properties='Excel8.0;HDR=Yes'" 'HDR=Yes cn.Open rs.Open "select * from[sheet1$]", cn, adOpenKeyset, adLockOptimistic If Not rs.BOF Then rs.MoveFirst rs.Move (n) For i = 0 To n rs.MovePrevious o = rs.Fields.Item(0).Value If Option1.Value = True Then r0 = rs.Fields.Item(2).Value ElseIf Option2.Value = True Then r0 = rs.Fields.Item(1).Value End If 依據(jù)上述設(shè)計的異常值剔除系統(tǒng),對某齒輪的齒距誤差測量數(shù)據(jù)進行粗大誤差的剔除。該齒輪的設(shè)計齒數(shù)z=48,模數(shù)m=4,分度圓壓力角α=20°。齒輪齒距偏差的測量屬于精密測量的范疇,所以選用多種判別法進行綜合判斷,當(dāng)判別時運行結(jié)果相同時,則認(rèn)為某測量數(shù)據(jù)應(yīng)該剔除,否則需慎重處理。 以該齒輪所測量的48個齒距偏差數(shù)據(jù)為實驗數(shù)據(jù),取不同數(shù)量的測量數(shù)據(jù)用4種判別法依次進行異常值的判定和剔除。表3為該齒輪齒距偏差測量數(shù)據(jù)。 表3 齒輪48個齒距偏差測量值 單位:μm 根據(jù)第2節(jié)對4種粗大誤差判別準(zhǔn)則的分析,選用肖維勒準(zhǔn)則對48個齒輪偏差數(shù)據(jù)進行處理,系統(tǒng)運行結(jié)果如圖2所示。 圖2 肖維勒法判別運行結(jié)果 由系統(tǒng)運行結(jié)果可以看出,在48個齒距偏差數(shù)據(jù)中,有3個齒距偏差數(shù)據(jù)-84.3、112.5、97.6是異常的,即為粗大誤差值。 齒距偏差數(shù)據(jù)為48個時,選用格拉布斯準(zhǔn)則且置信度α=0.05時進行異常值的判定與剔除,沒有判別出粗大誤差。取齒距偏差中的23個齒距偏差數(shù)據(jù)進行判定,運行結(jié)果如圖3所示。 圖3 格拉布斯法判別運行結(jié)果 當(dāng)用格拉布斯判別法進行判別時,從運行結(jié)果可以看出,在對混入3個粗大誤差的相同48個齒距偏差數(shù)據(jù)進行處理時,沒有判斷出粗大誤差;當(dāng)取21個齒距偏差,其中存在1個異常值的數(shù)據(jù)進行判別時,檢測出粗大誤差值為-84.3。 當(dāng)使用拉伊達法對含有3個異常值的48個齒距偏差數(shù)據(jù)進行判定時,檢測出3個異常值,分別為-84.3、112.5、97.6。當(dāng)對其中含有1個異常值的11個數(shù)據(jù)進行判定時沒有判定出異常值,運行結(jié)果如圖4所示。 圖4 拉伊達法判別運行結(jié)果 當(dāng)使用狄克遜法對含有3個異常值的48個齒距偏差進行檢測,判別出3個粗大誤差值,其運行結(jié)果同拉伊達判別法;當(dāng)對其中10個齒距偏差數(shù)據(jù)進行判別時,剔除1個含有較大誤差的正常齒距偏差測量值。 通過粗大誤差判定系統(tǒng)的運行結(jié)果分析,可以得到4種判別法的特點及適用性。拉伊達法和肖維勒判別法在數(shù)據(jù)量比較大時,可以快速判別出粗大誤差值;狄克遜判別法可以一次剔除多個異常值;當(dāng)1組測量數(shù)據(jù)中含有1個異常值時,適合用格拉布斯法進行異常值的判別與剔除。 在齒輪誤差測量的過程中,要求具有較高的測量效率以及較高測量精度,所以在進行齒輪測量數(shù)據(jù)進行異常值判別及剔除時,可以用多種方法對同一組齒輪誤差數(shù)據(jù)進行異常值的判定,如可以分別使用拉伊達準(zhǔn)則和狄克遜準(zhǔn)則對誤差數(shù)據(jù)進行異常值的判定剔除,當(dāng)判定結(jié)果相同時,可以認(rèn)定為異常值,否則要對檢測數(shù)據(jù)慎重處理;數(shù)據(jù)量較少時,使用前述方法判定后,可以用格拉布斯判別法對數(shù)據(jù)再次進行精確的判定。 齒輪誤差的分析評價是建立在齒輪誤差實際測量數(shù)據(jù)基礎(chǔ)之上的。在對齒輪誤差數(shù)據(jù)進行異常值判定時,要綜合運用多種判別準(zhǔn)則進行異常值的判定及剔除,以保證齒輪誤差數(shù)據(jù)的穩(wěn)定性和精確性。通過對4種判別法的分析,以及用設(shè)計的粗大誤差剔除系統(tǒng)對齒輪齒距偏差的數(shù)據(jù)預(yù)處理實驗,驗證了4種判別法在齒輪齒距偏差數(shù)據(jù)預(yù)處理中的科學(xué)性以及適用性。對齒輪測量數(shù)據(jù)預(yù)處理方法的研究,進一步完善了齒輪測量數(shù)據(jù)誤差的處理方法;在齒輪測量過程中,可以有效地避免因為人為因素或者環(huán)境因素而摻入異常測量值,保證后續(xù)齒輪誤差分析評價工作中所用數(shù)據(jù)的有效性和科學(xué)性。
2 異常值判剔除系統(tǒng)設(shè)計
2.1 系統(tǒng)結(jié)構(gòu)
2.2 主要模塊及原理
3 齒輪測量數(shù)據(jù)的異常值剔除
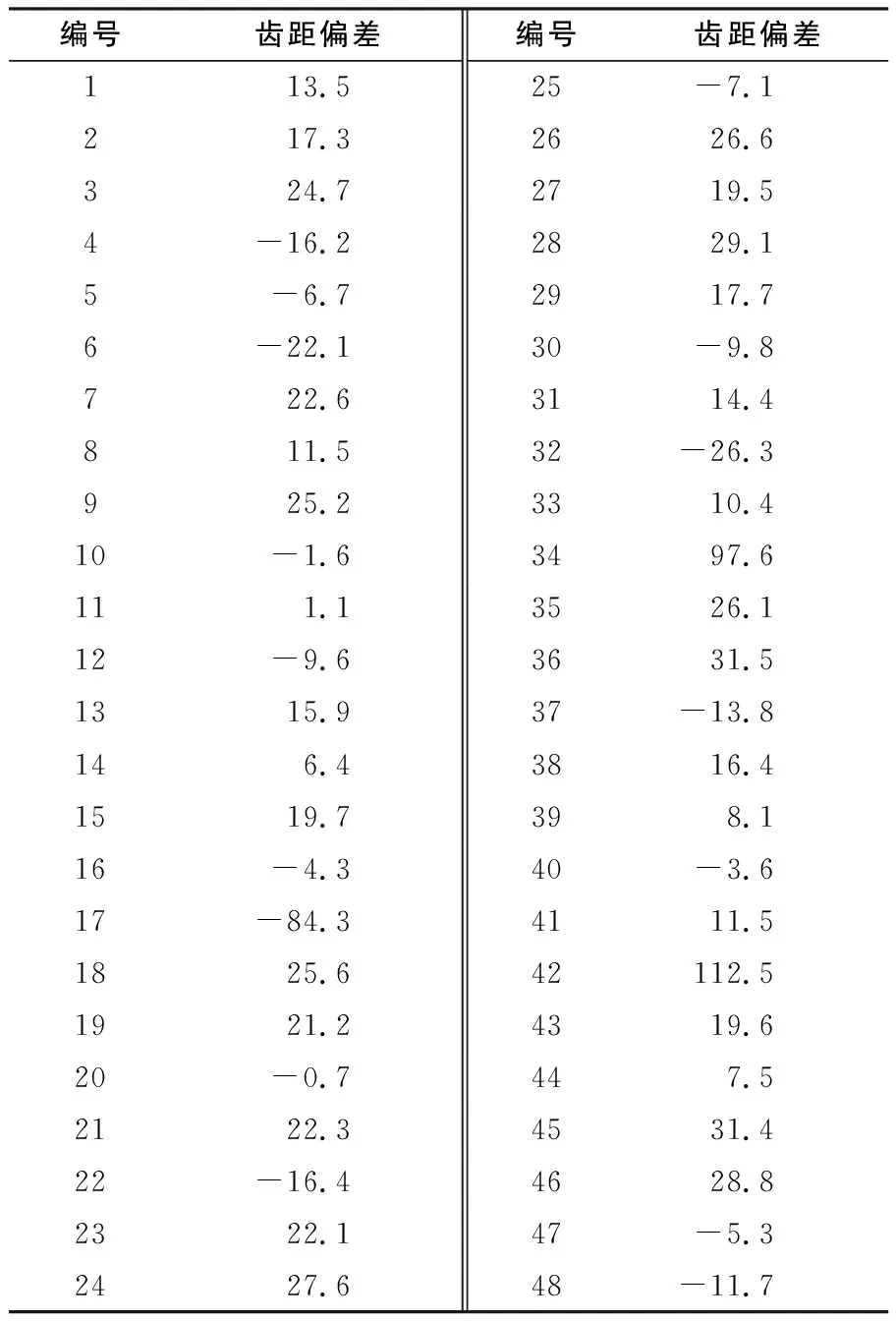
3.1 肖維勒判別法實驗
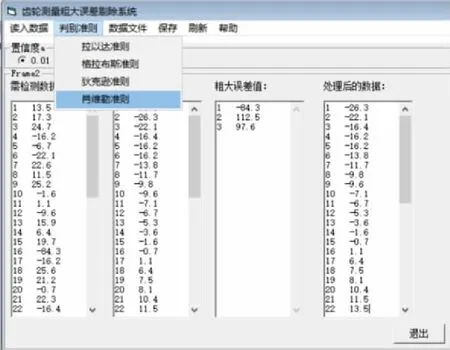
3.2 格拉布斯判別法實驗

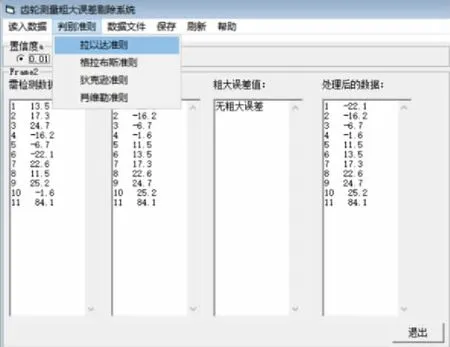
3.3 拉伊達判別法實驗
3.4 狄克遜判別法實驗
3.5 測量結(jié)果分析
4 結(jié)語

