SPSS軟件在數學建模競賽中的應用實踐

徐燕

[摘 要] SPSS軟件菜單化操作、圖表化的輸出特點是非統計學專業人員進行數據分析的有利工具。該文以2019年全國大學生數學建模競賽D題為例，以SPSS23軟件為工具，簡述該軟件在數學建模競賽中的應用，對數據進行相關分析、多元線性回歸分析和殘差分析等。

[關鍵詞] 數學建模;SPSS;相關分析;多元線性回歸;殘差分析

[基金項目] 2019年度高等學校中青年教師國內訪問學者項目資助

[作者簡介] 徐 燕（1981—），女，博士，廣州民航職業技術學院人文社科學院數理統計學專業副教授，南方醫科大學生物醫學工程學院訪問學者，主要從事統計學方法和應用教學與研究。

[中圖分類號] G642.0? ? [文獻標識碼] A? ? [文章編號] 1674-9324（2020）23-0331-03? ? [收稿日期] 2019-10-08

一、引言

SPSS軟件是當前世界上應用最廣泛的統計軟件之一，特別是對于非統計學專業人員，其菜單化操作、圖表化輸出的風格體現了其自動化、智能化操作平臺發展的成果。使用SPSS軟件，我們幾乎可以完全自動的自變量的預變換、篩選、模型優化、檢驗等工作。因此，SPSS軟件是一個深受廣大用戶的喜愛的強大的統計工具。

信息技術的飛速發展，產生了海量的數據。如何管理、分析和使用大數據是當前市場迫切的需求，從全國大學生數學建模競賽近年來的頻頻出現的大數據相關的題目也可以感受的到。作為非統計學專業的大專生，對于復雜的數據統計分析方法和工具接觸并不很多，如何讓這些學生快速入門和掌握一門有利的數據分析軟件工具、完成數據分析和建模等任務就是我們近幾年來數學建模培訓教學研究的重點。

二、2019年全國大學生數學建模競賽D題簡述

空氣污染對生態環境和人類健康危害巨大，通過對PM2.5等“兩塵四氣”濃度的實時監測可以及時掌握空氣質量，對污染源采取相應措施。由于國控點監測數據的實時性和經濟性不足，而自主研發時效性和經濟性并優的微型空氣質量檢測儀的監測數據可能受到溫度等氣象學因素的影響，以及設備本身隨著使用時間的延長可能產生監測誤差，因此我們需要對自建點監測數據進行檢驗和校正，提高其精確度。我們首先需要對自建點數據與國控點數據進行描述性統計分析和探索性分析，尋找導致自建點數據與國控點數據差異的因素，最后建立模型對自建點數據進行校準和預測。

監測數據可能受到溫度等氣象學因素的影響，我們通過相關分析探索變量之間的關系，再通過散點圖初步發現變量之間的回歸關系，進而采用多元回歸分析進行建模，并對模型進行殘差分析。我們以競賽提供的監測數據為例，使用SPSS23進行數據分析和建模。

三、SPSS23數據分析和建模應用

（一）建立數據文件

競賽提供的Excel數據文件，SPSS軟件可以直接讀取Excel數據文件，需要對變量進行適當的定義，從而生成完善的SPSS數據文件。

（二）相關分析

SPSS軟件中提供了“相關”子菜單，其中雙變量（Bivariate）過程可以實現連續性變量的相關分析。

1.操作過程。（1）“分析”→“相關”→“雙變量”，打開“雙變量相關”對話框;（2）將“PM2.5”與“溫度”“濕度”“風速”“壓強”“降水量”選入“變量”列表框中;（3）單擊“確定”按鈕。

2.結果分析。相關分析結果如表1所示，PM2.5與風速和溫度存在負相關關系（Pearson r<0，P<0.001），溫度的增大，PM2.5有減小的趨勢;PM2.5與壓強、降水量和濕度有正相關關系（Pearson r>0，P<0.001），隨著壓強或降水量或濕度的增大，PM2.5有增大的趨勢。

由相關分析的結果，PM2.5等監測變量指標與溫度等氣象學變量有相關關系，因此，提示我們進行下一步的多元回歸分析。

（三）多元線性回歸分析

SPSS軟件中提供了“回歸”子菜單，其中線性（Linear）過程可以實現多元線性回歸分析。

1.操作過程。第一步：做散點圖，觀察變量之間的趨勢。因為有多個變量，所以做散點圖矩陣。（1）“圖形”→“圖表建構程序”，打開“圖表建構程序”對話框，選擇“散點”，將右側出現的散點圖矩陣圖表拖入畫布中，單擊“確定”，繪制散點圖。（2）在輸出文件中雙擊圖形區域，進入編輯狀態，選擇“元素”→“增加趨勢線”，在圖形中添加回歸線。

從散點圖矩陣可以看到，PM2.5與風速和溫度存在負相關關系，PM2.5與壓強、降水量和濕度有正相關關系，與相關分析結果一致，并且變量之間呈現一定的直線關系，因此，提示我們進行下一步的多元線性回歸分析。

第二步：多重線性回歸分析，如圖1。（1）“分析”→“回歸”→“線性”，打開“線性回歸”對話框;（2）將“PM2.5_1”選入“因變量”列表框中，將“PM2.5”“溫度”“濕度”“風速”“壓強”“降水量”選入“自變量”列表框中;（3）在“方法”下拉列表框中選擇“逐步”;（4）單擊“確定”按鈕。

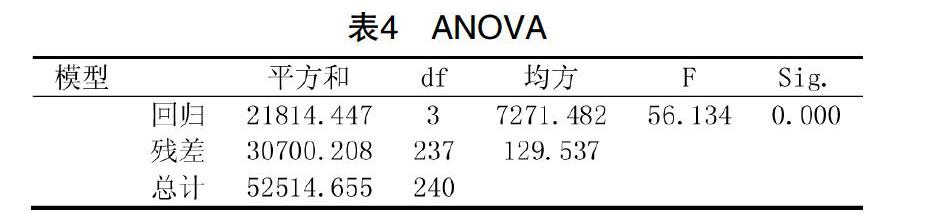
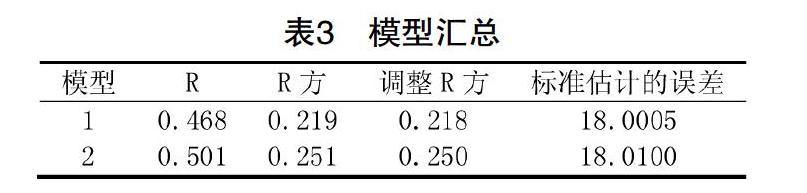
由于進行了變量篩選，SPSS首先給出了每一步模型的輸入/移出變量，展示了變量的篩選過程，如表2（迭代步驟較多，僅展示前兩個模型的結果）。第二，SPSS給出了模型的匯總，報道了決定系數R、R方和調整的R方，R方的值越接近于1說明模型的擬合效果越好，如表3。第三，SPSS給出了模型的ANOVA檢驗，報道了變異的分解、自由度、均方和F值、P值，P<0.05說明模型有統計學意義，如表4。最后，SPSS給出了模型的參數，以及各個系數的假設檢驗，從而我們可以寫出所建立的多元線性回歸方程。

第三步：殘差分析，首先對殘差的獨立性進行檢驗，可以在上述回歸過程中“統計量”子對話框匯總選擇“Durbin-Watson檢驗”，如圖2。輸出結果如表5，Durbin-Watson值為1.980，通過查統計表，與界值進行比較說明滿足獨立性。然后，SPSS軟件的“圖形”模塊可以輸出殘差直方圖和P-P圖，從圖中可以看出，模型的殘差沒有嚴重的偏離，基本服從正態分布。因此，由殘差分析說明所建立的模型具有較好的擬合效果。

四、討論

相關分析與回歸分析關系密切，一般有相關分析發現變量之間的相關性，相關系數r反映了兩個變量之間的密切程度，下一步利用散點圖判斷變量之間的線性或非線性關系，然后利用回歸分析進行建模，回歸系數β反映了自變量對因變量的平均數量變化關系。

多元線性回歸模型可以采用“向前”“向后”“逐步”等多種回歸分析方法來進行自變量的篩選，這些方法在分析中可以相互對比討論，同時結合人工篩選。

回歸分析有嚴格的使用條件，在擬合時需要不斷對這些條件進行檢驗判斷。回歸模型建模步驟一般包括如下：①做散點圖觀察變量之間的變化趨勢;②對數據的分布特征進行探索和檢驗，進行預變換，使其滿足回歸分析的數據要求;③進行多重線性回歸分析，建立基本模型;④進行殘差分析，分析模型的擬合效果，討論離群點和多重共線性問題。經過以上過程后，可以得到統計學上認可的模型，下一步還應當結合專業背景，將分析結果應用到實際中去檢驗其實用價值，討論實際應用中存在的問題。

五、總結

我們以2019年大學生數學建模D題為例，利用SPSS軟件建立了有效的校準模型.SPSS軟件是非統計學專業的大專生解決數據分析、數據建模問題的有利工具，其菜單化、圖表化的特點讓非統計學專業的大專生能夠快速入門、輸出結果結構化簡單明了，易于理解和應用。

參考文獻

[1]張文彤，鄺春偉.SPSS統計分析基礎教程（第3版）[M].北京：高等教育出版社，2017.

[2]武松，潘發明.SPSS統計分析大全[M].北京：清華大學出版社，2014.

[3]林建忠.回歸分析與線性統計模型[M].上海：上海交通大學出版社，2018.

[4]汪東華.多元統計分析與SPSS應用（第二版）[M].上海：華東理工大學出版社，2018.

Application Practice of SPSS Software in Mathematical Modeling Competition

XU Yan1，2

（1.Academy of Humanities，Guangzhou Vocational and Technical College of Civil Aviation，Guangzhou，Guangdong 510403，China;

2.College of Biomedical Engineering，Southern Medical University，Guangzhou，Guangdong 510515，China）

Abstract：The menu-based operation and graphical output characteristics of the SPSS software are useful tools for non-statistical professionals to carry out data analysis.Taking problem D of National College students' Mathematical Modeling Competition in 2019 as an example，this paper briefly describes the application of SPSS23 software in mathematical modeling competition，and carries on the correlation analysis，multiple linear regression analysis and residual analysis，etc.

Key words：mathematical modeling;SPSS;correlation analysis;multiple linear regression;residual analysis