常見函數不等式證明問題解法研究

◇ 廣東 鐘琴玲

函數不等式證明問題是高考的熱點，它涉及一次函數、二次函數、指數函數、對數函數、三角函數等組合成的函數以及導數、不等式知識，滲透數學抽象、邏輯推理、直觀想象、數學運算等數學核心素養.函數不等式的證明多與函數的單調性結合，還涉及構造新的函數，以及抽象出一些不能準確計算的數據，滲透化歸與轉化、數形結合、函數與方程等思想方法，對學生綜合運用知識的能力要求較高.這就要求教師在平時教學中要多向學生滲透數學思想，引導學生深入理解知識之間的共性以及數學中的通性通法，為綜合應用知識打下基礎.

1 構造函數，通過求導、求最值證明

在解決證明不等式成立問題時，一種重要的方法就是構造函數，然后通過求導判斷函數的單調性，再求最值，通過判斷函數的最值與某個定值的大小關系，從而證明不等式成立.有些題目可能比較復雜，需要多次構造函數，從而達到解決問題的目的.

(1)討論f(x)的單調性；

(2)若f(x)存在兩個極值點x1，x2，證明：

(1)f(x)的定義域為(0，＋∞)，

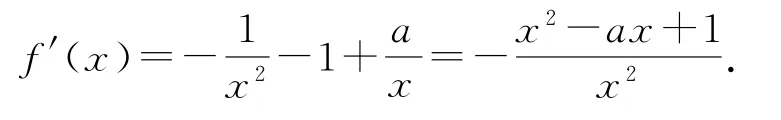
若a≤2，則f′(x)≤0，當且僅當a＝2，x＝1時f′(x)＝0，所以f(x)在(0，＋∞)單調遞減.

若a＞2，令f′(x)＝0，得

(2)由(1)知，f(x)存在兩個極值點，當且僅當a＞2.由于f(x)的兩個極值點x1，x2滿足x2－ax＋1＝0，所以x1x2＝1，不妨設x1＜x2，則x2＞1.由于

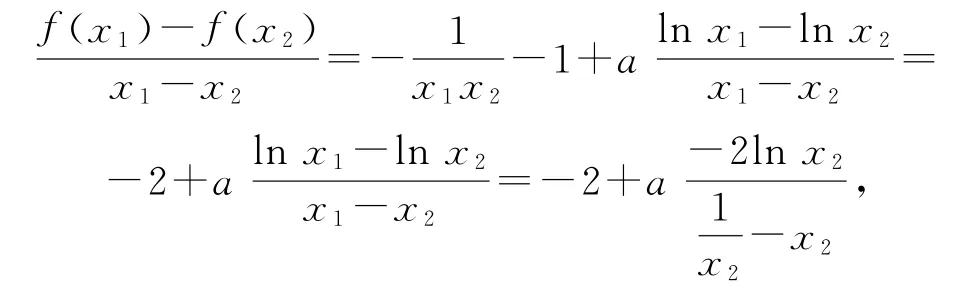
第(1)問討論函數的單調性是為第(2)問作鋪墊，由第(1)問的判斷可將a 的范圍縮小在(2，＋∞)內.第(2)問證明不等式成立，充分體現了化歸與轉化的思想，先將原不等式的證明等價轉化為證明另一個相對簡單的不等式，再構造新的函數，通過求導，判斷函數的單調性，求出最值，從而使不等式得證.解題時，要時刻關注第(1)問對第(2)問的影響，通過構造新函數來解決問題的思路要明確.構造函數時應注意盡量避免構造分式函數，若第一思路是構造分式函數，則應思考能否將其轉化為整式函數，因為分式函數的導數一般會比整式函數的導數復雜.解決此題必須具備很強的邏輯推理能力和數學運算能力.

當m≤2，x∈(－m，＋∞)且ln(x＋m)≤ln(x＋2)，故只需證明當m＝2時，f(x)＞0.當m＝2時，函數f(x)＝ex－ln(x＋2)，f′(x)＝ex－在(－2，＋∞)單調遞增，又f′(－1)＝－1＜0，f′(0)＝＞0，故f′(x)＝0在(－2，＋∞)上有唯一實根x0，且x0∈(－1，0).當x∈(－2，x0)時，f′(x)＜0，當x∈(x0，＋∞)，f′(x)＞0，從而當x＝x0時，f(x)取得最小值.由得，故

綜上，當m≤2時，f(x)＞0.

本題先通過放縮，將含參量的不等式證明轉化為不含參量的不等式證明，然后通過求最值，判斷函數的最小值大于0，從而證得結論.將含參數問題轉化為非參數問題，大大降低了難度，是解題的一種非常重要的思路.

2 構造函數，通過單調性定義證明

在證明函數不等式時，有時需要轉化思想，即在證明兩個自變量的大小關系時，將其轉化為證明函數值的大小關系，或者在證明兩個函數值大小關系時，將其轉化為比較兩個自變量的大小關系，而這種轉化的橋梁主要是函數的單調性定義.

(1)若f(x)在(－∞，＋∞)上單調遞增，求實數a 的取值范圍；

由已知可得f(x1)＝f(x2)＝0，不難發現x1≠1，x2≠1，不妨設x1＜x2，故可整理得

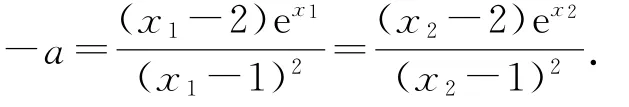
要證x1＋x2＜2等價于證x1＜2－x2，由x1＜1＜x2，可知2－x2＜1，g(x1)－g(2－x2)＝g(x2)－.令h(x)＝(x－2)ex＋xe2－x，h′(x)＝(x－1)ex＋(1－x)e2－x＝(x－1)(exe2－x).

當x＞1，即x＞2－x 時，h′(x)＞0，所以h(x)在(1，＋∞)上單調遞增，h(1)＝(1－2)e＋e＝0，所以當x＞1時，h(x)＞0，所以h(x2)＞0，從而g(x1)＞g(2－x2)，故x1＜2－x2，即x1＋x2＜2.

此題是將待證明的不等式等價轉化為x1＜2－x2，將x1，2－x2看成兩個自變量，通過構造函數g(x)，先判斷函數值g(x1)，g(2－x2)的關系，再結合函數g(x)的單調性，證得結論.

3 將不等式轉化為兩個函數比較大小

將不等式轉化為兩個函數比較大小，用其中一個函數的最小值與另一個函數最大值進行比較，從而證明函數不等式成立.

(1)求a，b；

(2)證明：f(x)＞1.

設函數g(x)＝xlnx，則g′(x)＝1＋lnx，所以當x∈(0，)時，g′(x)＜0，當x∈(，＋∞)時，g′(x)＞0，故g(x)在()單調遞減，在，＋∞)單調遞增，從而g(x)在(0，＋∞)上的最小值g()＝.設函數，則h′(x)＝e－x(1－x)，所以當x∈(0，1)時，h′(x)＞0，當x∈(1，＋∞)時，h′(x)＜0，故h(x)在(0，1)單調遞增，在(1，＋∞)單調遞減，從而h(x)在(0，＋∞)的最大值為

綜上，當x＞0時，g(x)＞h(x)，即f(x)＞1.

此題若采用構造函數求最值的方法很難獲解，而采取將證明待證不等式等價轉化為證明g(x)＞h(x)，分別求函數g(x)的最小值和函數h(x)的最大值，經過計算得到函數g(x)的最小值與函數h(x)的最大值相等，但兩個函數取最值時對應的自變量不相等，從而當x＞0時，g(x)＞h(x)，證得原不等式成立.

函數導數解答題中貫穿始終的是數學思想與方法，在含有參數的試題中分類與整合思想是必要的，解題時常把不等式問題轉化為函數最值問題、把方程的根轉化為函數的零點等.

函數不等式證明問題涉及知識面廣，如求函數的零點、函數的導數、函數單調性與最值等，有時還不能直接求出函數最值，需要進一步構造函數，判斷最值的大小，對學生的綜合能力要求較高.解題方法靈活多樣，技巧性強，計算強度大，要求學生有較強的邏輯思維能力、運算能力、分析問題與解決問題的能力.本文介紹的3種方法是比較常用的，但因為問題形式千變萬化，考題亦常考常新，因此在備考的各個階段都應重視函數不等式證明問題的教與學，提高學生解決此類問題的能力.