淺談導函數隱零點范圍的估計策略
◇ 江西 李樹森
利用導數研究不等式,需要構造函數,將所研究的問題轉化為函數的最值來處理,在求函數的最值時,常常需要確定導函數的零點,有時會碰到導函數有零點但求解其零點比較困難的情況,此時稱此零點為隱零點.雖然將這個零點虛設出來,通過整體代入能簡化函數并研究其函數值的范圍,但有時需要將這個零點的范圍較為精準地進行估計,才能達到解決問題的目的,因此如何確定隱零點的范圍,成為解決問題的關鍵.本文從解不等式、目標函數反解、二分法、放縮法、利用單調性等角度介紹其范圍的估計方法.
1 構造隱零點的不等式求解隱零點的范圍
分析問題轉化為fmin(x)≥0,因此研究導函數,利用零點存在判定定理判斷導函數零點存在,但求解困難,通過虛設零點,將其零點與參數a 之間的關系整體代入,簡化函數,根據條件構造含零點的不等式,通過解不等式確定零點的范圍,最后利用函數思想可以求解參數a 的范圍.
解由已知條件可得fmin(x)≥0,且

令φ(x)=aexx2-(a+1)(a>0),則

當x∈(0,+∞),φ′(x)>0,所以φ(x)在(0,+∞)上為增函數,又φ(0)=-(a+1)<0,而
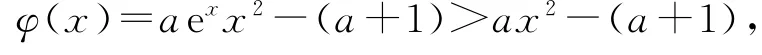
當x∈(0,x0)時,φ(x)<0,f′(x)<0,所以f(x)在(0,x0)上為減函數;
當x∈(x0,+∞)時,φ(x)>0,f′(x)>0,所以f(x)在(x0,+∞)上為增函數.
又因為φ(x)=aexx2-(a+1)在(0,+∞)上為增函數,且0<x0≤1,所以0=φ(x0)≤φ(1),由0≤φ(1),可得

利用零點存在判定定理,判定零點的存在,找到隱零點x0與參數a 的關系aex0=,將其整體代入函數中,簡化目標函數得,從而構造了隱零點x0的不等式,解出零點的范圍,這即為所求的隱零點的范圍.
2 通過隱零點代換,利用多項式函數的臨界值反解出隱零點的邊界
分析解決不等式f(x)>kx 恒成立,可以通過分離參數,得到構造函數將問題轉化為求目標函數g(x)的最小值(最小值的取值范圍),借助導數,判斷導函數g′(x)存在零點,此零點不易求解,再通過虛設零點,利用零點的關系整體代入,求出函數g(x)的最小值,其值不是一個具體的數,需要估計零點的精確的范圍,將其最小值的范圍限定在一個很小的范圍內,從而確定整數k 的最大值.
解當x∈(1,+∞)時,f(x)>kx 恒成立,等價于當x∈(1,+∞)時,恒成立.
因此當x∈(1,m)時,h(x)<0,即g′(x)<0,則g(x)在x∈(1,m)上單調遞減;當x∈(m,+∞)時,h(x)>0,即g′(x)>0,則g(x)在x∈(m,+∞)上單調遞增.所以當x∈(1,+∞)時,
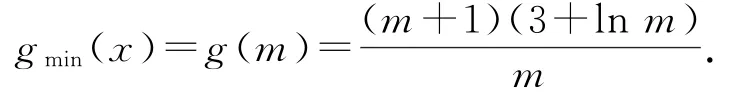

3 利用二分法估計隱零點的范圍
分析由題意函數有2個零點,可轉化為研究函數y1=-k 與函數y2=2xe-x-ex的圖象有2 個交點,即研究函數y2=φ(x)=2xe-x-ex的單調性和極值的范圍,通過求導得φ′(x)=e-x(2-2x-e2x),此函數的零點不易求解,故可虛設零點,整體代入,預設存在零點的一個范圍,利用二分法,將零點存在的區間逐步縮小,以便準確求出極值的范圍,順利尋找到滿足條件的整數k的最小值.
解由題意函數g(x)有2個零點,可轉化為函數y1=-k 與函數y2=2xe-x-ex的圖象有2個交點,令φ(x)=2xe-x-ex,則


當x∈(-∞,x0),h(x)>0,即φ′(x)>0,所以φ(x)在(-∞,x0)為增函數;當x ∈(x0,+∞),h(x)<0,即φ′(x)<0,所以φ(x)在(x0,+∞)為減函數.


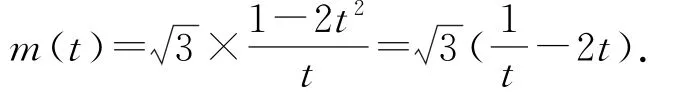

在判斷隱零點的范圍時,我們常在預判的過程中將范圍擴大,借助“二分法”思想,將其范圍一分為二,重新確定一個新的有解范圍,直至將隱零點精確在一個很小的范圍內,往往能夠達到解題的目的.在本題中,開始預設零點x0∈(0,1),發現函數的極大值范圍較大,通過“二分法”將其零點x0縮小到一個小的區間(0,),此時函數φ(x)的極大值φ(x0)∈(-,-1),從而確定了符合條件的最小整數k.其實二分法思想是一種逼近的思想,最終將零點控制在一個精準的范圍內.
4 放縮函數,通過解不等式確定零點的邊界
分析證明不等式f(x)<ex-x2-3x+1,可構造函數g(x)=xlnx+ex-x2-2x,研究其最小值,通過求導得g′(x)=ex+lnx-x-1,此零點不可求,虛設零點,整體代入得g(x0)=(x0-1)lnx0-再確定零點的范圍,即可證明.
解設g(x)=xlnx +ex-x2-2x,則g′(x)=ex+lnx-x-1,g″(x)=ex+-1,因為x>0時,g″(x)=ex+-1>0,所以g′(x)在(0,+∞)上為增函數,又因為



即

本題在不等式證明過程中,通過構造函數,并且運用了兩次求導,利用零點存在定理判定了零點的存在,通過虛設零點、整體代換進行求解.其中取點估算是此題的難點,本題中通過對代換后的目標函數g(x0)=(x0-1)lnx0-(x0+1)2+分析,要證明g(x0)>0,注意到(x0-1)lnx0>0,將目標函數放縮得g(x0)=(x0-1)lnx0-(x0+1)2+,通過解不等式-(x0+1)2+,得到零點的一個邊界點-1,通過計算確定隱零點類似本題中運用放縮法取點,在近幾年的高考中常常考查.
5 構造隱零點的等量關系,利用函數的單調性確定隱零點的范圍
分析為了研究函數f(x)的最小值,可借助導數工具.f′(x)=(x-1)ex+2a(x+1),利用零點存在判定定理判定零點存在,發現此導函數零點求解很困難,需要虛設此零點,整體代換,簡化目標函數.但是為了求出函數f(x)的最小值g(a)的值域,此時需要準確確定隱零點的范圍,利用隱零點x0與a 之間的關系,利用函數思想,確定函數的單調性,借助反解出零點的范圍,從而求出函數g(a)的值域.
解因為f′(x)=(x-1)ex+2a(x+1)(x>0),令φ(x)=f′(x),則φ′(x)=xex+2a>0,則f′(x)在(0,+∞)上為增函數,f′(0)=2a-1<0,f′(1)=4a>0,故?x0∈(0,1),使得f′(x0)=0,即(x0-1)ex0+2a(x0+1)2=0,即
又因f′(x)在(0,+∞)上為增函數,且f′(x0)=0,所以當x∈(0,x0)時,f′(x)<0,則f(x)在(0,x0)上為減函數;當x∈(x0,+∞)時,f′(x)>0,則f(x)在(x0,+∞)上為增函數.又因為,令得,即h(x)在(0,1)為減函數,又因為h(0)=,h(1)=0,
所以0≤x<1,即0≤x0<1,所以
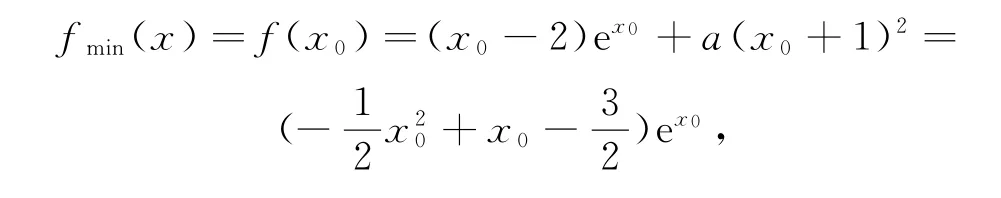

這是一道比較復雜的導函數零點不可求的問題,這種題的解題通法是先利用零點存在原理,找出零點x0的大致區間,再繞開x0的具體值,轉而判斷導函數在這個區間的單調性,同時借助f′(x0)=0整體代換,進而將問題化繁為簡.本題之所以比較復雜,就是因為本題設置了一個參數0<a≤,通過這個參數的取值范圍使得零點精確的范圍原形畢露,為求最小值的值域立下了汗馬功勞.
處理函數與不等式問題,常常需要研究導函數的零點,這是處理不等式問題的關鍵之處,解題時先利用零點存在判定定理,預設出零點存在的范圍,虛設此零點,整體代換簡化目標函數.預設的零點在研究最值(極值)范圍過大時,往往需要將零點的范圍進一步縮小.若遇到隱零點的關系式無參數時,常常利用“二分法”思想將范圍縮小,或者借助目標函數的臨界值反解出零點的邊界點,并驗證該邊界點的函數值的正負號,將零點范圍縮小;遇到參數時,往往需要借助參數與隱零點之間的關系,將問題轉化為函數問題,利用函數的單調性,來估算其范圍.確定范圍的方法有很多,在研究問題時需要同學們靈活多變,才能輕松破解此類問題.

