彈道導彈群目標跟蹤分裂算法研究

靳俊峰， 曾 怡， 廖圣龍

(1.中國電子科技集團公司第三十八研究所， 安徽合肥 230088；2.孔徑陣列與空間探測安徽省重點實驗室， 安徽合肥 230088)

0 引言

對武器系統來說，為實現彈頭目標動能攔截，需要在大氣層外60 km甚至更高位置即完成目標穩定跟蹤、攔截計算、導彈發射等工作，否則攔截高度過低時來襲彈頭的速度過大，攔截彈速度若低于來襲彈頭，攔截效果較差。對預警系統來說，若彈頭群目標分裂過早，即彈頭群內目標相對距離還很小時即對群內目標進行單獨跟蹤，會經常出現混批、錯批現象，降低目標跟蹤精度、浪費傳感器資源，給后續的目標識別、軌道外推等帶來很大難度；若彈頭群目標分裂過晚，采用群質心跟蹤時彈頭目標的識別、軌道推算時間會過晚，導致武器系統錯失攔截的最佳窗口。因此如何解決群目標盡早分裂與群內目標關聯正確率之間的矛盾是導彈防御系統的核心問題。

迄今為止已經有很多群目標跟蹤算法，基于貝葉斯框架的空間群目標跟蹤技術[1]在分析空間目標運動特征的基礎上構造能夠描述“群”的運動特征參數和結構變量，在貝葉斯框架下對群目標進行跟蹤，相對無群中心時提升了目標數目估計的穩健性，但該算法主要考慮了空間群目標，且MCMC-Particle算法建模復雜、計算量大；基于群目標的多目標概率數據關聯算法[2]采用等效回波及其統計中心為量測，并將跟蹤空間中任一關聯門內的所有回波看作一個群，通過關聯門是否較差、多少回波位于關聯門交叉區內的判別及其相對于不同關聯中心概率的計算，確定交叉區域內回波的歸屬；基于UKF濾波的可變多模型(VUF)跟蹤方法[3]采用多模型的結構適用于跟蹤任意階段的彈道導彈，有效提高了跟蹤精度，降低了計算復雜度；基于多假設的群目標跟蹤算法[4]利用多假設處理復雜數據關聯問題的能力，對群中的單個目標形成假設航跡，保證跟蹤穩定性。此外，機動群目標跟蹤算法研究[5]、基于空域法的UCAV群目標編群策略研究[6]和基于相對位置矢量的群目標灰色精細航跡起始算法[7]等也從群的劃分、群質心的計算、基于空域進行目標編群、群起始等角度對群目標跟蹤問題進行了研究。

以上算法均從群中心計算、群目標關聯、彈道目標濾波等角度進行彈道導彈群目標跟蹤技術研究，對于何時進行群目標分裂、分裂后如何維持穩定跟蹤及如何降低群內目標錯誤關聯概率甚少涉及，且群內目標會由于相互遮擋導致檢測不穩定，給群分裂帶來更大難度，而該問題是目前導彈防御系統中亟待解決的問題。本文從群目標的形成與分裂過程、IMM-UKF框架、最優分配算法等角度進行問題建模分析，分析了影響群目標分裂的各種因素，結合最近鄰思想和極大似然函數算法，提出了基于IMM-UKF的彈道導彈群目標分裂算法，采用Pareto改進算法進行了多目標規劃問題求解。仿真和實測結果表明，該算法能夠達到群目標盡早分裂與群內目標關聯正確率之間的平衡。

1 群目標跟蹤

1.1 群目標形成及跟蹤

群目標跟蹤是一種復雜情況下的多目標跟蹤，目前主要有以下三種形式：

1) 群跟蹤，無單個航跡：計算群信息，無群內航跡信息；

2) 群跟蹤，加簡化的航跡：計算群信息，并在群內維持簡化的航跡；

3) 單獨航跡跟蹤，加群信息：維持各個目標單獨的跟蹤航跡，群信息用來補充。

在彈道導彈防御中，預警時間有限，需要完成導彈軌道定軌、發落點計算、目標分類識別、威脅度排序及攔截打擊等一系列復雜工作流程，必須盡早、盡可能地保證對單個目標的高精度穩定跟蹤。群目標質心跟蹤方法無法保證跟蹤精度，會影響彈道推算及發落點預報；目標的RCS起伏特性也被群質心取加權平均淹沒，無法進行準確的目標分類識別。

鑒于彈道導彈群目標跟蹤的復雜性，本文采用“單獨跟蹤航跡加群信息”的群目標跟蹤方式處理密集回波時的跟蹤問題。

群目標跟蹤架構如圖1所示，過程如下：

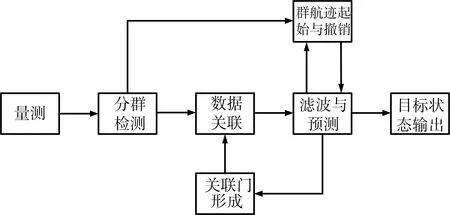
圖1 群目標跟蹤架構

1) 接收量測進行分群檢測；

2) 分群完成后對群航跡進行關聯門計算，形成量測-航跡分配矩陣；

3) 采用最優分配算法進行量測-航跡分配計算；

4) 對分配最好的量測-航跡配對進行濾波預測，并對群信息進行更新；

5) 與群內航跡未關聯上的回波，根據群分裂距離判斷是否起始新航跡，更新群信息；

6) 對航跡采用IMM-UKF濾波算法進行濾波平滑，對連續丟點群航跡進行航跡撤銷；

7) 輸出目標信息，顯示群信息及群內航跡。

1.2 IMM-UKF框架

為進行彈道目標關機點判別、加速度估計、再入大機動跟蹤，需要考慮多運動模型框架，利用跟蹤過程中某些參數的異常變化進行特征事件的檢測。交互多模型(Interacting Multiple Model，IMM)[8]算法是處理多模型跟蹤的主流方法，其基本思想是：假設一個模型集合Μ作為任何時刻目標真實模型的可能候選；運行一系列子濾波，而每個子濾波都是基于Μ中一個確定的模型；基于這些子濾波的結果，按照某種原則產生目標狀態的整體估計。

鑒于彈道目標運動和測量模型的非線性，本文采用UKF進行狀態估計。UKF以UT變換為基礎，采用卡爾曼線性濾波框架。它通過選取一些確定的采樣點，更好地近似隨機變量經非線性變換以后的均值和方差，從而減少了因非線性系統線性化所產生的誤差，并且避免了對非線性函數求導的麻煩。

IMM-UKF的基本框架[9]如圖2所示。本文中并未使用文獻[3]中提出的可變多模型方法，而是使用了彈道動力學模型、當前統計模型、勻速運動共三種固定模型的組合，可變多模型需要根據模型、概率、目標高度和速度方向動態選擇模型集合，在跟蹤過程中需要不斷對各種模型進行初始化，且彈道目標機動性很強，模型的選擇容易出錯。三種固定模型計算量并沒有大幅度增加，減少了模型選擇出錯概率。

圖2 IMM-UKF框架

1.3 群內目標數據關聯算法

為解決群內密集目標的關聯問題，采用文獻[10]提出的最優分配算法，量測與航跡建立全局關聯分配矩陣，充分利用目標散布特性，并基于大數據分析隸屬度權重，采用最優分配算法進行點航跡配對。關聯概率大小取決于特征向量的隸屬度和權向量，通過歸一化模糊評判向量U和權向量W構成綜合隸屬度評判函數，航跡i與量測j的目標關聯概率為

(1)

關聯概率dij若小于閾值Pth，則認為航跡i與量測j無法關聯，在關聯矩陣中取值為0；若大于Pth，則可用于構建基于綜合隸屬度函數的關聯矩陣IM：

(2)

式中，n表示航跡數，m表示量測數。該算法通用性和擴展性較好，且對群內目標關聯正確率達到95%以上，適合群目標分裂后的關聯。

2 群目標分裂算法

2.1 問題描述

文獻[11]對空間密集多目標進行了理論分析，將數據關聯區劃分為無錯誤關聯區(Unambi-guous Association，UA)、不穩定區域(Unstable Region，UR)和有錯誤關聯但航跡跟蹤穩定區(Misassociation Without Track Loss，MWTR)三類區域，如圖3所示。目標間距大于5倍的標準差為UA區域，2～5倍之間為MWTR區域，2倍以下為UR區域。

圖3 多目標數據關聯區域圖

UA區域內目標由于間隔足夠大，不會發生錯誤關聯，群間目標因空間位置間隔較大位于UA區域；UR區域內目標錯誤關聯經常發生，導致跟蹤不穩定，會頻繁刪除航跡，航跡跟蹤精度很差，群目標分裂過程中會位于UR區域；MWTR區域內航跡關聯會出錯，且航跡個數少于實際的目標個數，但航跡不會因為關聯錯誤發生刪批，群內目標未分裂前位于MWTR區域。UR區域隨著采樣周期增大而增大，UA區域和MWTR區域隨著采樣周期減小和檢測概率提高而增大。群目標分裂的關鍵在于如何減小UR區域持續時間，使得分裂出的新目標盡快位于UA區域。

由于群目標飛行密集特性，傳感器對群目標的一次波束照射會完成多個群內目標的檢測，形成多個量測信息。假設此時群內僅有一批目標獨立跟蹤，該單獨跟蹤航跡會選擇一個綜合隸屬度最大的量測進行數據關聯和濾波，其余的檢測用于形成暫時航跡。此時群目標分裂算法核心在于選擇分裂距離，使得暫時航跡可以形成群內單獨跟蹤的航跡，該問題可描述如下：

(3)

給定傳感器和群目標跟蹤場景時，即確定了目標個數n、TG、采樣周期τ、檢測概率PD，以及量測誤差σr、σβ、σγ。

該算法不僅限制于一個群目標，對于多個群目標問題可通過分群算法劃分為單個子群，最終簡化為單個群目標的求解。

2.2 問題求解

群目標分裂算法需要找到一個分裂距離區間使得目標函數最優，求解過程中會與檢測概率、采樣周期、目標位置、量測噪聲、濾波器收斂性能、數據關聯算法正確性等諸多因素相關，是一個典型的多目標規劃問題。

對于多目標規劃問題，記它的變量可行域為S，相應的目標可行域Z=f(S)，給定一個可行點x*∈S，若?x∈S，有f(x*)

為找到群目標分裂距離的Pareto最優解，采用Pareto分析法，又稱為ABC主次因素分類法。根據影響目標函數的主要特征，進行分類排隊，分清重點和一般。

ABC主次因素分類法分為5個步驟：

1) 針對不同的分析對象和分析內容，收集有關數據；

2) 對各數據進行統計匯總；

3) 編制ABC分析表；

4) 繪制ABC分析圖，了解各個影響因素比重；

5) 確定重點需要調整的參數。

Pareto改進是指一種變化，在沒有使任何目標函數變壞的前提下，使得至少一個目標函數變得更好。一方面，Pareto最優是指沒有進行Pareto改進的余地狀態；另一方面，Pareto改進是達到Pareto最優的路徑和方法。該求解算法需要迭代運行多次才能找出最優解，無法用于實時目標跟蹤，解決辦法為通過離線數據訓練出特定采樣周期、檢測概率、量測噪聲下的多組分裂距離次優解，傳感器在實時跟蹤時根據參數選擇相應分裂距離即可，可事后結合實測數據進行分裂距離調優。

3 性能評估

假設雷達的距離測量誤差σr=30 m，方位測量誤差σβ=0.2°，仰角測量誤差σγ=0.2°，發現概率PD=0.8，虛警概率Pf=1×10-6，雜波分布服從泊松分布，濾波器采用基于彈道導彈動力學、當前統計模型和CV模型混合的UKF濾波方法，群內目標數據關聯算法采用最優分配算法[10]。四批目標再入飛行場景，一個彈體目標、一個彈頭目標加兩批假目標伴飛，4個目標距離間隔在200～ 1 200 m之間，速度從1 400 m/s變化為1 950 m/s、數據率為1 s，目標從240 km運動至150 km，飛行時長為100 s。

在此情況下，按照文獻[11]中的分析結果，3個目標間隔達到5倍測量誤差即距離150 m時即可位于穩定跟蹤區域，但對雷達測量數據來說，此時3個目標的仰角和方位間隔達不到5倍測量誤差，且彈道濾波需要在地心系中進行模型計算，耦合了距離、方位、仰角三個維度誤差，目標回波會交疊在一起，航跡跟蹤波門會相互重疊。

經過對仿真數據分析，三批目標在距離上相對位置比較固定，角度上無法分辨，航向、速度、RCS值等參數比較接近，因此在權向量選擇上歸一化距離特征具有最大的權重，達到了0.7，而其他特征由于無法區分目標，僅占比0.3，權向量的參數選擇可通過學習或者先驗知識獲取，提高了關聯矩陣建立的靈活性。

圖4是按照Pareto方法離線計算最優分裂距離為608 m時，群內4個目標并列飛行時的跟蹤航跡。4個目標原始回波有互相遮擋現象，部分位置也存在虛警，4個目標都有自己獨立的航跡，在復雜情況下僅在檢測丟點時發生了一次交叉，表明該算法可以計算出最優分裂距離，即能保證群內目標盡早分裂，又能保證群目標關聯正確率最好。

圖4 四批目標IMM-UKF最優分裂跟蹤結果

圖5為采用減小的最優分裂距離400 m進行跟蹤，可以看到群內6個目標并列飛行，雖然跟蹤時長較長，但T2與T5、T3與T6間關聯交叉次數明顯較多，跟蹤質量下降，盡早分裂沒有帶來跟蹤性能提升。

圖5 減小最優分裂距離為400 m后跟蹤結果

實驗表明，基于IMM-UKF框架的群目標分裂算法能夠計算出最優的分裂距離，按照該分裂距離可實現對群內單個目標盡早獨立跟蹤，在實際應用中具有重要意義。因為彈道導彈突防時雷達探測回波中有大量相互靠近目標，雷達要精確跟蹤20 s以上，才能得到有效的發落點預報；同時要繼續通過運動特性、幾何特性、光學特性等不斷地進行目標識別、威脅排序，隨后進行攔截打擊，整個過程只有幾分鐘。通過盡早對單個目標進行跟蹤，可提前完成發落點預報、彈頭識別，為攔截贏得寶貴時間。

4 結束語

彈道導彈目標為突防需要，通常在飛行中段會釋放多批誘餌、干擾機等形成群目標進行伴飛。由于群內目標之間空間相互靠近，運動特性相似且相對速度較小，因此需要較長的飛行時間積累才能在空間上完全分開，甚至到再入段才能由于質阻比不同在空間上完全分開。對武器系統來說，越早完成群目標分裂，跟蹤時長越長，武器準備時間就越充分，但另一方面如果群目標分裂過早，在跟蹤過程中極易發生混批、錯批等問題，影響測量精度，浪費雷達資源，也無法穩定進行軌道推算、目標識別等工作。

本文提出了基于IMM-UKF的彈道導彈群目標分裂算法：首先分析群目標的形成及跟蹤策略，論述了IMM-UKF濾波框架和群內目標數據關聯算法，然后對群目標分裂算法進行了數學建模，分析了影響群目標分裂的各種噪聲因素，最后提出了基于IMM-UKF框架的彈道導彈群目標分裂算法，并采用Pareto 改進算法求得分裂距離最優解。仿真結果表明，該算法能夠達到群目標盡早分裂與群內目標關聯穩定度之間的平衡。

在實際應用中，群目標分裂算法并不能孤立使用，而是需要綜合考慮群目標管理策略、濾波器跟蹤穩定性、傳感器測量噪聲等因素，通過對多次測量數據的事后分析來統計逼近最優解的分裂距離。