基于耦合協調度的大理河流域徑流和輸沙關系分析

賈 路，任宗萍※，李占斌，李 鵬，徐國策，張鐵鋼，楊媛媛

（1. 西安理工大學省部共建西北旱區生態水利國家重點實驗室，西安 710048；2. 旱區生態水文與災害防治國家林業和草原局重點實驗室，西安 710048；3. 水利部牧區水利科學研究所，呼和浩特010020）

0 引 言

黃河是中華民族的母親河，隨著氣候變化與人來活動的影響，黃河流域生態環境狀況及自然條件發生了巨大變化，黃河流域的健康和高質量成為一項重大國家戰略，黃河流域的發展關系著流域內人民的生產和生活的長遠發展[1-2]。黃河中游地區占據了黃河流域的大部分面積，該區域位于世界水土流失最為嚴重的地區之一-黃土高原，因此治理黃河流域的水沙變化問題一直是治黃工作的核心問題[3-4]。自20 世紀50 年代開始，中國在黃土高原地區實施了大規模的水土保持工程建設，特別是淤地壩工程的建設，有效地攔截了黃土高原地區產生的泥沙，調節了徑流，阻止泥沙進入黃河，黃河徑流和泥沙顯著減少[5]。同時，近幾十年全球氣候發生顯著變化，全球變暖的趨勢日益加劇，極端事件頻發，已經受到國際社會的普遍關注，氣候變化進一步加劇黃河流域水資源的供需矛盾[6-7]。氣候變化有可能會加速全球水文循環，這對水沙關系的變化將產生非常重大的影響。研究氣候變化條件和人類活動作用下水文過程和水沙變化的狀況是目前水文學和水土保持的熱點問題之一。

徑流和泥沙作為流域極具重要價值的資源，在流域社會、經濟和生態環節中扮演著重要的角色。許多研究調查了氣候變化和人類活動影響下的徑流和輸沙的變化特征。曹麗娟等[8]對未來氣候變化條件下黃河和長江流域極端徑流影響預估進行了研究。歐陽潮波等[9]對60 a 來黃河河龍區間水沙變化特征及人類活動的影響進行了評價。高海東等分析了2000—2017 年河龍區間輸沙量銳減的原因[10]。盡管關于徑流和輸沙對氣候變化和人類活動時空變化響應及歸因分析的研究已經被進行了研究，并取得了很多的研究成果。但是有一個事實是至關重要的，由于過去的研究大多數是基于單變量角度對流域水文變量間的關系包括水沙關系進行的研究，所以這成為造成識別的變量之間的變化存在巨大的差異[11-12]。在自然界中，地表水、大氣、植被、土壤和地下水等環境要素之間存在復雜的相互作用[13]，使用單變量的分析方法可以讓事情變得簡單、便捷。然而，單變量的分析方法只關注了單個變量的變化（例如徑流或輸沙），這與現實差別較大，不能完全揭示對氣候變化和人類活動的水沙響應。因此，有必要基于多變量的視角研究徑流和輸沙的變化特征。

大理河流域作為黃河的二級支流[14]，位于中國典型的干旱和半干旱區域。同時，由于大理河流域地處中國黃土高原地區，地形破碎，溝壑區密度大，水土流失比較嚴重，耕地資源和水資源非常有限。這一情況對該區域工農業發展來說，是十分不利的。眾所周知，大理河流域的徑流呈現顯著下降[15]，這使得當地水資源的供需矛盾進一步加劇，同時伴隨著嚴重的泥沙問題。在過去的許多時間，關于大理河流域的氣候變化和人類活動影響下的徑流變化和輸沙變化的研究已經取得了顯著的成果。但是，大部分研究重視探索造成徑流變化和輸沙變化等單個變量變化的氣候變化和人類活動因素，關于徑流和輸沙之間關系的研究還需要不斷探索和深入研究。徑流和輸沙之間的水沙關系作為流域物質循環中至關重要的環節，二者之間的關系具有緊密的聯系，這是水土保持研究關注的重點問題之一[16]。一直以來研究徑流輸沙之間的關系對于優化流域水土流失治理工作，評估流域水土保持效益都是必要的。一旦流域徑流和輸沙和之間的關系存在突變，這意味著流域的水文機制和水沙關系已經發生了改變，對于工程設計工作來說也必須進行改變，才能有效地興利除害。因此，基于多變量視角對大理河流域徑流和輸沙的變化關系進行探索至關重要，對在氣候變化和人類活動的巨大影響條件下指導當地進行水資源規劃和水土保持具有重要意義。

本文通過Mann-Kendall 檢驗研究徑流輸沙的變化趨勢，基于耦合協調度理論和Pettitt 檢驗方法構建流域徑流和輸沙之間關系的突變點的識別方法并進行診斷，并通過Copula 方法進行了驗證，探討了造成大理河流域徑流和輸沙關系變化的可能驅動因素。研究有助于進一步深化對大理河流域水沙關系變化的認識，為大理河流域水土保持工作開展提供一定的科學依據。

1 材料與方法

1.1 研究區概況

大理河流域位于中國黃河流域中游（109°14′～110°13′E，37°30′～37°56′N），綏德水文站為流域出口水文站[17]，如圖1 所示。大理河為無定河的第二大支流，起源于靖邊縣白于山東測的五臺山，流經橫山縣、子洲縣、綏德縣，在綏德縣東北部注入無定河。大理河全長159.9 km，流域面積3 904.24 km2，比降3.16‰，流域地面坡度較大，大部分在15°以上，主要支流有小理河、岔巴溝、駝耳巷溝等。流域西高東低，地形起伏較大，海拔796～1 744 m。流域主要土壤類型為黃綿土和新積土，屬于黃土峁狀丘陵溝壑區。流域內坡長多大于200 m，溝谷切割深度多大于50 m，使得流域形成了許多坡陡溝深的小流域。流域土壤侵蝕為嚴重，經過幾十年的水土保持綜合治理，水土流失量明顯下降。

1.2 數據來源

本文所使用的徑流和輸沙數據來源于黃河水文年鑒，時間序列為1960—2015 年。降水數據是來源于國家地球系統科學數據中心的柵格降水量數據（http：//loess.geodata.cn），時間序列為1960—2017 年，空間分辨率為1 km×1 km，時間分辨率為月，該數據使用全國496 個獨立氣象觀測點數據進行了驗證，驗證結果可信，該數據可以準確的反映全流域降水的變化分布情況。淤地壩數據來源于2011 年第一次全國水利普查。中國年度植被指數（NDVI）空間分布數據集是基于連續時間序列的 SPOT/VEGETATION NDVI 衛星遙感數據（http：//www.resdc.cn/data.aspx?DATAID=257），采用最大值合成法生成的1998 年以來的年度植被指數數據集。該數據集有效反映了全國各地區在空間和時間尺度上的植被覆蓋分布和變化狀況，對植被變化狀況監測、植被資源合理利用和其他生態環境相關領域的研究有十分重要的參考意義。

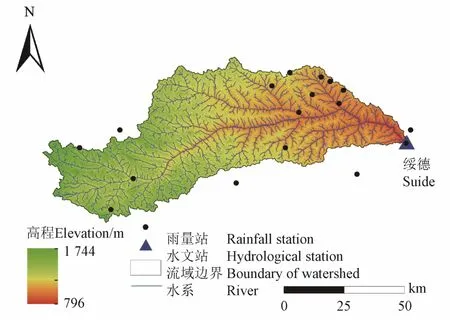
圖1 陜西省大理河流域地理位置 Fig.1 Location of the Dali River Basin, Shaanxi province

1.3 研究方法

1.3.1 Mann-Kendall 檢驗

Mann-Kendall（M-K）檢驗[18]是一種非參數的判斷數據序列變化趨勢的分析方法，常被廣泛使用在氣象和水文序列的趨勢檢驗中，本文采用Mann-Kendall 檢驗捕捉徑流量、輸沙量、NDVI 以及其他變量的變化趨勢。

1.3.2 耦合協調理論

耦合最早是作為一個物理學的概念，指2 個或2 個以上系統或運動形式通過各種相互作用而彼此影響的現象[19]。隨著研究的發展，耦合概念被逐步引入到生態學領域中，并被廣泛使用[20]。多個系統相互作用耦合度模型可以用一下模型表示[21]

式中Cn為n 元系統的耦合度；u1…un分別為第一個子系統到第n 個子系統對總系統有序度的貢獻，計算方法如下

式中ui為第i 個子系統對總系統有序度的貢獻；uij為第i個子系統中第j 個指標的歸一化值；wij為第i 個子系統中第j 個指標的權重，每個子系統中指標的權重計算使用熵權法進行計算。

在計算每個子系統的熵權時，必須先進行歸一化處理，這里采用最大最小值法進行歸一化處理：

當uij為數值越大對系統越好時（正向歸一化）

當uij為數值越小對系統越好時（負向歸一化）

式中xij為子系統第i 個指標的第j 個時序的值。

根據多元系統的耦合度模型，容易得到徑流和輸沙2個子系統之間的耦合度模型，可以表示成以下形式

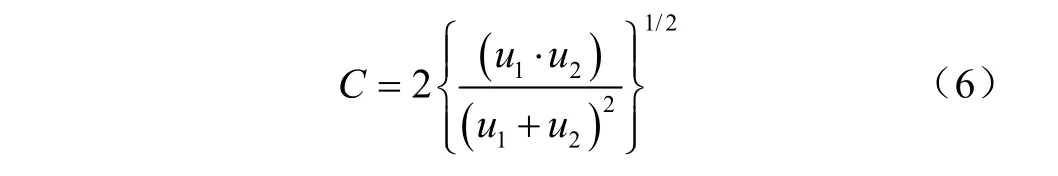
式中C 為徑流輸沙二元系統的耦合度。在本研究中徑流和輸沙子系統的指標為12 個月的月徑流量和月輸沙量，每個指標的權重計算采用熵權法，假定徑流越大對系統越好，輸沙越少對系統越好。

由于耦合度指標在有些情況下卻很難反映出子系統整體“功效”與“協同”效應，耦合度各子系統指標的上下限取自各指標的極值，而極值存在動態、不平衡的特性，單純依靠耦合度判別有可能產生誤導。為此，進一步采用耦合協調度模型來評判徑流子系統和輸沙系統交互耦合的協調程度，計算公式如下

式中D 為耦合協調度；C 為耦合度；T 為徑流子系統與輸沙子系統的綜合調和指數，它反映徑流子系統與輸沙子系統的整體協同效應或貢獻；a、b 為待定系數，實際中常常認為兩個子系統的重要性相同[21]，所以a=b=0.5。

1.3.3 邊際分布函數與Copula 函數

邊際分布函數[22]是統計學中一種描述單變量與其概率分布的函數，不同的分布函數可以刻畫不同的變量的特征。在本研究中，指數分布函數、耿貝爾分布函數、皮爾遜三型分布函數和廣義極值分布函數被使用來擬合徑流和輸沙數據，同時通過計算4 種理論分布函數累積概率和經驗累積概率的R2來優選出最優的理論分布函數。

Copula 函數是一種可以用來描述多個變量聯合分布的一種連接函數[22]，由于它可以連接任何2 個邊際分布函數，因此使用起來十分方便。Copula 函數具有很多家族，其中阿基米德家族Copula 函數因為具有較少的參數，所以被廣泛使用。本研究中通過AIC 準則，從阿基米德家族Copula 函數的Frank Copula、Gumbel Copula 和Clayton Copula 3 種Copula 這種選出最優的Copula 來連接大理河流域徑流和輸沙的最優邊際分布函數，構建出最優的徑流輸沙最優Copula 分布函數。

1.3.4 Pettitt 突變點檢驗

Pettitt 檢驗法[23]采用Mann-Whitney 中Ut,n值檢驗同一總體中2 個樣本X1,…,Xt和Xt+1,…,XN，Pettitt 檢驗的零假設為沒有變化點，當|Ut,n|取最大值時對應的Xt被認為是可能的突變點。當P≤0.05 時認為數據中存在均值變異點。其顯著性水平可由下式計算

當P≤0.05 時認為數據中存在均值變異點。

2 結果與分析

2.1 徑流和輸沙變化趨勢

大理河流域1960—2015 年各月及年徑流量和輸沙量的變化趨勢計算結果如表1 中所示。徑流在3、4、5、8、10、11 月以及年尺度均呈現顯著的下降趨勢，其中3、4、10 月以及年尺度的M-K 統計量絕對值較大，表明徑流下降幅度較大，1 月的徑流呈現不顯著的增加趨勢，其他月份的徑流呈現不顯著的下降趨勢。在1960—2015年間，各月輸沙以及年尺度輸沙均呈現顯著的下降趨勢，相比同一月份的徑流變化趨勢而言，輸沙的M-K 統計量絕對值均高于徑流，說明輸沙的下降幅度更大。在1960—2015 年間大理河流域的徑流與輸沙變化均存在明顯的下降趨勢，但徑流與輸沙的變化幅度呈現出不協調的特點。

表1 1960—2015 年大理河流域徑流量和輸沙量變化趨勢 Table 1 Trends of runoff and sediment load in the Dali River Basin from 1960 to 2015

2.2 徑流輸沙關系變異診斷

2.2.1 徑流子系統與輸沙子系統的指標變化

本研究中認為徑流越大對系統越好，輸沙越少對系統越好，選取每年12 個月的徑流量和輸沙量分別作為兩個子系統的構成指標，對每個指標即每個月的徑流量和輸沙量進行了歸一化處理，使用熵權法計算每個指標的權重，如表2。

表2 的結果顯示，1960—2015 年間6 月的徑流量在一年中權重最大，11 月的徑流量權重最小，4、5、7、8、9、10 月的徑流量權重較大。在1960—2015 年間，輸沙量在8 月的權重最大，2 月和7 月的權重較大。徑流的權重值變異系數為0.58，輸沙的權重值變異系數為0.51，徑流量年分配權重比輸沙更為不穩定。

表2 1960—2015 年大理河流域徑流量和輸沙量權重 Table 2 Weights of runoff and sediment load in the Dali River Basin from 1960 to 2015

2.2.2 徑流和輸沙耦合協調度的變化趨勢與突變點

根據耦合協調度理論計算了大理河流域徑流子系統和輸沙子系統的耦合協調度，并通過Pettitt 檢驗方法識別了徑流輸沙耦合協調度的突變點年份，它反映了大理河流域徑流和輸沙之間關系的變異特征（圖2）。

圖2a所示的是1960—2015年間大理河徑流輸沙耦合協調度的時間序列圖，最大值為0.75，最小值為0.42，根據M-K 趨勢檢驗結果表明徑流輸沙耦合協調度呈現顯著下降趨勢，說明大理河流域徑流輸沙關系協調程度不斷下降。圖2b 表明大理河流域徑流輸沙耦合協調度的突變點為1996 年，在1996 年徑流和輸沙之間存在顯著突變點，通過對突變點前后的2 個耦合協調度的子序列進一步進行Pettitt 檢驗，發現不存在顯著突變點，這表明大理河流域徑流和輸沙關系只在1996 年存在明顯的不同。

2.2.3 基于Copula 函數的徑流輸沙突變點驗證分析

為了對基于耦合協調度理論識別的徑流和輸沙關系變異點診斷結果進行驗證，本研究采樣Copula 函數構建了徑流和輸沙之間的最優聯合分布累積概率，并識別了突變點（圖3）。

圖2 1960—2015 年大理河流域徑流量和輸沙量耦合協調度變化及其突變點 Fig.2 Changes of coupling coordination of runoff and sediment load and its change-points in the Dali River Basin from 1960 to 2015

圖3 1960—2015 年大理河流域徑流和輸沙之間的最優聯合分布累積概率 Fig.3 Cumulative probability of optimal Copula joint distribution of runoff and sediment load in Dali River Basin from 1960 to 2015

指數分布函數、耿貝爾分布函數、皮爾遜三型分布函數和廣義極值分布函數等4 種理論分布函數被使用來擬合大理河流域1960—2015 年的年徑流和年輸沙數據，通過K-S 檢驗分別檢驗了年徑流和年輸沙數據，發現年徑流和年輸沙都通過了K-S 檢驗，這表明4 中理論分布函數都可以用來描述年徑流和年輸沙，同時使用線性矩法估計了4 種理論分布函數的參數，分別通過計算年徑流和年輸沙的經驗累計概率與4 種理論分布函數的累積概率之間的R2，根據R2最大原則選取該分布函數為最優的分布函數。結果表明，大理河流域1960—2015 年年徑流的最優分布函數為皮爾遜三型分布，年輸沙的最優分布函數為指數分布。圖3a、3b 分別為大理河流域1960—2015 年年徑流量、輸沙量的最優分布函數累計概率與經驗累積概率的時間序列圖。基于AIC 準則，從阿基米德家族Copula 函數的Frank Copula、Gumbel Copula 和Clayton Copula 三種Copula 中選出Frank Copula 作為最優的Copula 來連接大理河流域徑流和輸沙的最優邊際分布函數，計算出來徑流和輸沙之間的聯合分布函數累積概率（圖3c）。根據M-K 趨勢檢驗對徑流和輸沙之間的聯合分布函數累積概率的分析可知，大理河流域徑流和輸沙之間的聯合分布函數累積概率呈現顯著下降趨勢，Pettitt 檢驗對徑流和輸沙之間的聯合分布函數累積概率分析結果表明大理河流域徑流和輸沙之間關系在1996 年存在顯著突變點（圖3d）。2 種徑流輸沙關系突變點的診斷方法表明，基于耦合協調度的徑流輸沙關系變異診斷方法可以準確的識別出徑流輸沙的關系突變點。

2.3 變異前后徑流輸沙變化特征分析

2.3.1 徑流輸沙變化特征分析

對比年徑流量-年輸沙量關系突變點前后，徑流與輸沙的年內和年際的變化特征，可以發現大理河流域1960—1996 年年徑流量為1.50 億m3和1996—2015 年徑流量為1.08 億m3，1996—2015 年期間相比1960—1996 年期間徑流量減少27.92%，減少幅度較小。1960—1996 年年輸沙量為0.43 億t 和1996—2015 年輸沙量為0.17 億t，1996—2015 年期間相比1960—1996 年期間輸沙量減少57.11%，輸沙的減少幅度比徑流的減少幅度高29.19 個百分點。1996—2015 年各月徑流量、輸沙量與1960 —1996 年各月徑流量、輸沙量相比較發現，除了12月徑流量相比突變前有所增加，其余各月徑流量均在減少；輸沙量在12 個月中均發生了明顯的減少現象，特別是在8 月份，徑流和輸沙的減少量最大（圖4）。

圖4 突變點前后徑流量和輸沙量年內分配 Fig.4 Annual distribution of runoff and sediment load before and after the change-point

2.3.2 徑流輸沙關系變異

徑流和輸沙關系突變點前后徑流和輸沙的散點圖，如圖5。由徑流和輸沙關系突變點前的徑流和輸沙相關圖（圖5a）可以看出，徑流輸沙關系可以被線性回歸方程描述，徑流和輸沙的決定系數R2為0.867 3（P<0.05），在統計學意義上，決定系數R2表示自變量可以解釋因變量的程度，因此，在1996 年之前大理河徑流對輸沙貢獻程度高達86.73%，單位的徑流輸沙能力較強。圖5b 突變點后大理河的徑流和輸沙相關圖表明，在1996—2015 年徑流輸沙關系也可以被線性回歸方程很好的描述，徑流和輸沙的決定系數R2為0.823 1（P<0.05），在1996 年后大理河徑流對輸沙貢獻程度降低到82.31%，下降幅度為5.10%，單位的徑流輸沙能力降低。

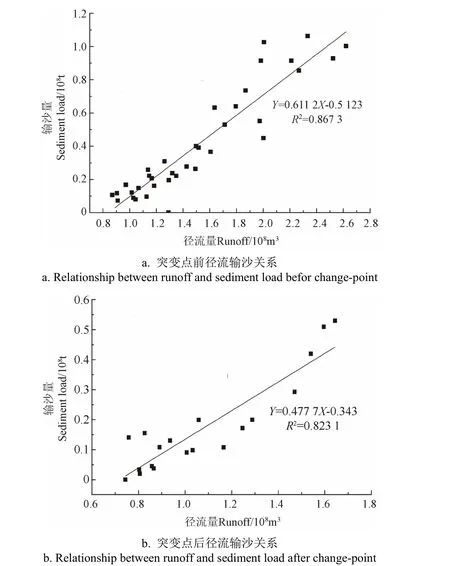
圖5 大理河流域突變點前后徑流輸沙關系 Fig.5 Relationship between runoff and sediment load before and after the change-point in Dali River Basin

2.4 氣候變化和人類活動對徑流輸沙變化的貢獻率

對徑流和輸沙變化影響的主要驅動因素包括氣候因素和下墊面因素[24]。本研究使用雙累積曲線分析兩者對大理河流域1960—2015 年徑流和輸沙變化的影響。

如圖6 所示為1960—2015 年大理河流域年降水量和年徑流量雙累積曲線（圖6a）、年降水量和年輸沙量（圖 6b）。從圖6a 中可以看出，大理河流域年降水量和年徑流量之間存在較弱的非一致性。圖6b 表明，大理河流域年降水量和年輸沙量之間存在明顯的非一致性關系。結合圖6，將降水和徑流、輸沙關系劃分為3 個時段，分別為1960—1971、1972—1996、1997—2015 年。將1960—1971 作為基準期，認為該時期降水徑流關系和降水輸沙關系未發生變化，具有一致性，定量分析氣候變化和人類會動對徑流和輸沙變化的貢獻率，如表3 所示。在1972—1996、1997—2015 年2 個時期人類活動對徑流和輸沙減少的貢獻率均遠遠高于氣候變化的影響，特別是在1997—2015 年時期，氣候變化對徑流和輸沙變化表現出增加的作用，這表明下墊面的人類活動是導致大理河流域徑流和泥沙減少的主要驅動力，這與劉曉燕等[25-26]人的研究結果一致。

表3 氣候變化和人類活動對大理河流域徑流輸沙貢獻率計算結果 Table 3 Calculation results of climate change and human activities' contribution to runoff and sediment load in the Dali River Basin

圖6 1960—2015 年大理河流域年降水量-徑流量和降水量-輸沙量雙累積曲線 Fig.6 Double accumulation curve of annual precipitation-runoff and precipitation-sediment load in the Dali River Basin from 1960 to 2015

3 討 論

3.1 淤地壩建設對徑流輸沙的影響

研究表明，黃河流域的年降水量并未發生顯著增加[27]，根據1960—2015 年大理河流域年降雨的M-K 趨勢檢驗結果表明，M-K 趨勢檢驗統計量的絕對值均小于1.96，這意味著全流域年降水量均呈不顯著的變化趨勢（圖7b）。對于黃土高原地區來說，人類活動變化中影響最為廣泛的就是20 世紀50 年代開始在黃土高原地區實施的水土保持工程，該工程主要包括林草工程、梯田建設和淤地壩工程的修建[28-29]。其中，因為淤地壩具有攔沙淤地的直接經濟效益，因而被黃土高原地區廣泛推廣使用，淤地壩工程的修建歷時最長，修建規模最大[30]。圖8 中所示為大理河流域1960—2011 年徑流量和輸沙量變化，其中實測輸沙量為綏德水文站的觀測值，實際輸沙量為淤地壩逐年攔沙量和實測輸沙量的加和。實測輸沙量的變化基本與實際輸沙的變化具有一致性。因此，實際輸沙量與徑流量的關系和實測輸沙量與徑流量的關系基本保持一致。根據李宗善等[31]的研究，黃土高原地區淤地壩已經超過10 萬座以上，效益明顯，直接發揮了攔截泥沙淤泥造地的功能，目前已經截留了280 億t 水土流失總量，2002 年淤地壩農田規模達到3 200 km2，糧食產量是梯田的2～3 倍。在大理河“7·26”特大暴雨洪水事件中，建設有完備淤地壩系的韭園溝流域相比對照流域洪峰流量消減達到8 倍，洪水含沙量只有對照流域的三分之一。根據2011 年全國第一次水利普查，大理河流域共有骨干淤地壩279 座（圖7a）。淤地壩的修建高峰期在20 世紀70 年代，同時2000 年后水利部實施淤地壩亮點工程，淤地壩的修建又出現了第二次高峰。淤地壩的修建直接攔截了大理河流域大量的泥沙，對流域徑流產生了再調節和再分配的作用，徑流的變化造成產沙輸沙能力的減弱，因而間接減少了輸沙量。

3.2 植被恢復對徑流輸沙變化的影響

自從1999 年中國政府在黃土高原地區實施了退耕還林政策，大規模的植樹造林工程顯著的增加了黃土高原的植被覆蓋度[32-33]。特別是在大理河流域，NDVI 從1999—2015 年明顯增加（圖9）。根據M-K 檢驗分析，1999—2015 年大理河流域NDVI 均值呈現顯著增加趨勢，與徑流和輸沙的變化趨勢相反。根據ULSE 土壤侵蝕的模型的原理，隨著植被的增加土壤侵蝕程度可以降低，植被在一定程度上阻止了泥沙的產生，減少了輸沙量[34]。根據梁越等[35]的研究，退耕還林后黃河河龍區間土壤侵蝕強度減弱，退耕還林工程對河龍區間減少作用從大至小呈現：中部-南部-北部。同時，研究表明由于近60年河龍區間降雨和降雨侵蝕力并未發生明顯變化趨勢，退耕還林后植被增加可能是小流域泥沙減少的主要推動力。

圖7 陜西省大理河流域骨干淤地壩空間分布與降雨量變化分布 Fig.7 Spatial distribution of check dam and precipitation in the Dali River Basin, Shaanxi province

圖8 大理河流域徑流量與輸沙量變化 Fig.8 Changes of runoff and sediment load in Dali River Basin

圖9 1999—2015 年大理河流域NDVI 均值變化 Fig.9 NDVI change in Dali River Basin from 1999 to 2015

4 結 論

1）在1960—2015 年，大理河流域的徑流與輸沙在各月及年尺度均存在顯著下降趨勢，而且徑流與輸沙的變化趨勢不協調不同步。

2）本研究構建了基于耦合協調度的徑流輸沙關系突變點診斷方法，識別出大理河流域徑流輸沙關系在1996年存在顯著突變點，同時基于徑流輸沙Copula 聯合分布累計概率驗證了該突變點確實存在，表明1996 年是大理河流域徑流輸沙關系發生變化的重要節點，本文方法具有很好的識別準確性。

3）大理河流域徑流輸沙關系突變后，徑流和輸沙均有所減少，徑流量減少27.92%，輸沙量減少57.11%，輸沙減少幅度大于徑流。徑流輸沙關系突變后，大理河徑流對輸沙貢獻程度相比徑流輸沙關系突變前，下降幅度為5.10%，徑流輸沙能力降低。

4）人類活動是影響大理河流域徑流輸沙變化的主要驅動力，淤地壩的修建影響著徑流和輸沙的變化，自退耕還林政策實施后，從1999—2015 年大理河流域NDVI 均值呈現顯著增加趨勢，對徑流和輸沙變化產生重要作用。