分離奇函數巧解函數對稱中心問題
2020-07-22 08:08:38梁宗明
數理化解題研究 2020年19期
關鍵詞:定義
梁宗明
(甘肅省蘭州市蘭化一中 730060)
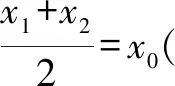
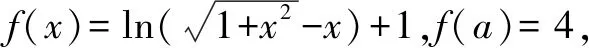
分析這個函數的圖象實際關于點(0,1)中心對稱,但是其對稱性隱藏很深,即使發現是對稱性問題,尋求函數對稱中心的計算量也非常之大,但是題目中都有f(a),f(-a),容易聯想起函數奇偶性,所以可以分離奇函數簡潔解決此類問題.
解法1 利用定義求出對稱中心
假設函數的對稱中心為A(a,b),在函數圖象上任取一點P(x,y),則對稱點Q(2a-x,2b-y)也在函數圖象上,即2b-y=f(2a-x).化簡之后與原函數是同一個函數,根據對應項系數相等,解得a=0,b=1,則f(-a)+f(a)=2,所以f(-a)=-2.
解法2 檢驗f(-x)+f(x)=定值.
f(x)+f(-x)
=ln1+2=2,
則f(-a)+f(a)=2,所以f(-a)=-2
解法3 分離奇函數.
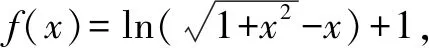
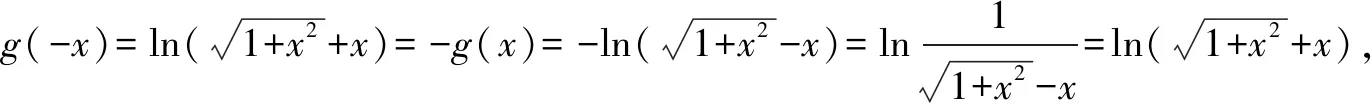
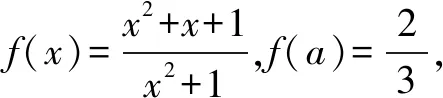
解法1 利用定義求出對稱中心.
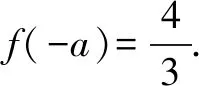
解法2 檢驗f(-x)+f(x)=定值
則f(-a)+f(a)=2,
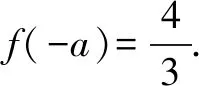
解法3 分離奇函數
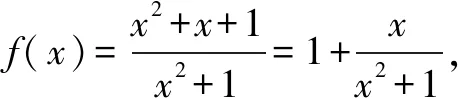
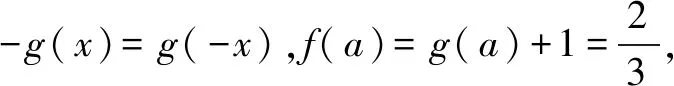
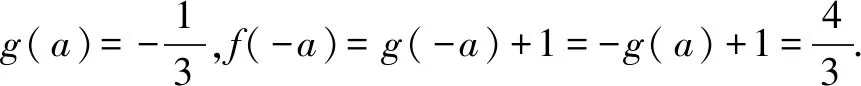
猜你喜歡
幼兒教育·父母孩子版(2022年4期)2022-05-08 21:35:35
中學生數理化(高中版.高考數學)(2021年3期)2021-06-09 06:09:14
中學生數理化(高中版.高二數學)(2021年12期)2021-04-26 07:43:38
中學生數理化(高中版.高二數學)(2021年2期)2021-03-19 08:54:04
海峽姐妹(2020年9期)2021-01-04 01:35:44
華人時刊(2020年13期)2020-09-25 08:21:32
VOGUE服飾與美容(2020年9期)2020-09-02 14:47:26
山東青年(2016年1期)2016-02-28 14:25:25
汽車維護與修理(2015年6期)2015-02-28 12:16:55
當代修辭學(2014年3期)2014-01-21 02:30:44

