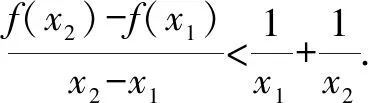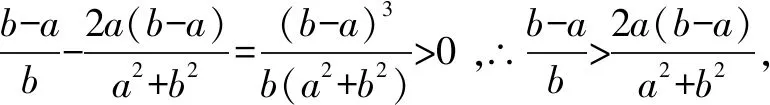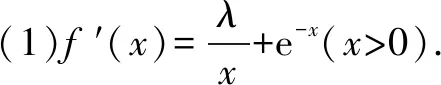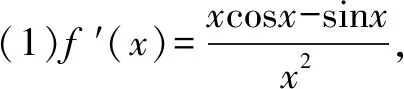拉格朗日中值定理的應用

武 婷 黃光鑫

(四川省成都市四川師范大學附屬中學 610000)

一、引言

拉格朗日Lagrange中值定理本是微分學中的一個重要定理，不在高中數學課本范疇之內，是否有必要教給學生呢？我們先看下面一個問題：

C.f(x)=ex+1D.f(x)=sin(2x+1)

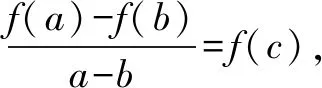
對于A選項：f′(x)=3x2-6x+3∈[0,+)，f(x)∈R，不滿足性質T，符合題意.對于B選項：f令x=tanα，則f′(x)轉化為當sin2α，cos2α>0時，則由四元均值不等式可知：當且僅當時，等號成立.∵g(α)為奇函數，∴f不滿足性質T，符合題意.對于C選項：f′(x)=ex+1，f(x)∈R，f′(x)∈R，滿足性質T.對于D選項：f′(x)=2cos(2x+1)，f(x)∈[-1,1]，f′(x)∈[-2,2]，滿足性質T.綜上：選A,B.

從上面的解法可以看出，對于學有余力的學生而言，對于想參加高校自主招生考試或者想參加數學競賽的學生而言掌握拉格朗日中值定理也是很有必要的！

二、拉格朗日Lagrange中值定理

拉格朗日Lagrange中值定理:如果函數f(x) 在閉區間[a,b]上連續，在開區間(a,b) 內可導，那么在(a,b)內至少存在一點ξ(a<ξ

三、拉格朗日Lagrange中值定理的應用

下面我們本著由易到難，循序漸進的原則介紹拉格朗日中值定理在解決高中數學題中的應用.

例2 [2019·安徽十校聯考]已知函數f(x)=lnx+ax+1(a∈R).(1)討論函數f(x)的單調性；

解(1)函數f(x) 的定義域為(0,+)當a≥0 時，f′(x)>0，f(x)在(0,+)上單調遞增；當a<0時，由f′(x)=0，得若單調遞增；若)，f′(x)<0，f(x)單調遞減.

綜上所述：當a≥0 時，f(x)在(0,+)上單調遞增；當a<0時，f(x)在單調遞增，在)上單調遞減.

(2)證明:由(1)知，當a≥0時，f(x)在(0,+)上單調遞增，不滿足條件.所以a<0，此時f(x)的極大值為由已知得-ln(-a)=0，故a=-1，此時f(x)=lnx-x+1.不妨設0

例3設函數f(x)=lnx，g(x)=2x-2(x≥1).

(1)試判斷F(x)=(x2+1)f(x)-g(x)在定義域上的單調性；

解(1)∵函數f(x)=lnx,g(x)=2x-2(x≥1),F(x)=(x2+1)f(x)-g(x)=(x2+1)lnx-(2x-2) 的定義域為[1,+)當x≥1 時，F′(x)≥0 恒成立，故函數F(x)在定義域[1,+) 上為增函數.

例4 [2019屆高三黃岡模擬]已知函數f(x)=λlnx-e-x(λ∈R).

(1)若函數f(x) 是單調函數，求λ的取值范圍；

(2)記函數g(x)=e1-x，則函數g′(x)=-e1-x，g(x)在[x1,x2]上滿足拉格朗日中值定理的條件，∴?ξ∈(x1,x2) 使得：g(x2)-g(x1)=-e1-ξ(x2-x1)=e1-ξ(x1-x2).∵x1<ξe1-x1(x1-x2) .