基于功率譜靈敏度的子結構損傷識別方法

方有亮， 李宗嬈，張穎，婁佳琪

(河北大學 建筑工程學院，河北 保定 071002)

近年來，國內外學術界和工程界對于結構損傷識別的研究十分廣泛和深入，并提出和發展了許多結構損傷識別方法.其中，功率譜密度是進行損傷識別與分析的有效用具.李曰兵等[1]采用廢止鐵路線鋼橋為試件，利用正弦掃頻波激振鋼橋,分析其損傷前后加速度響應功率譜密度的變化來進行損傷識別. Gilbert-Rainer[2]針對相關信號段和相應諧波的整數周期計算每個信號分量的功率譜，提出了一種基于固有頻率變化的梁式結構損傷檢測及損傷位置和損傷程度評估的新方法.鄭澤棟等[3]采用虛擬激勵法計算功率譜密度對結構損傷參數的靈敏度，并結合有限元模型修正，對平面框架結構和剪力墻結構進行損傷識別.然而，在求功率譜靈敏度時，直接求取響應功率譜關于結構損傷參數的偏微分比較困難.

另外，大部分方法在對大型復雜結構的損傷診斷時需要較多自由度信息以及測點，因此實際工程中存在模態參數測量不完整的問題.為了提高計算效率，很多子結構識別方法應運而生.鄭鴻飛[4]通過Guyan靜力凝聚法對無砟軌道模型進行自由度縮減來降低結構自由度數目，并計算討論了靜力、動力學分析在無砟軌道分析中的適用性.侯吉林等[5]利用子結構響應的線性組合，采用子結構隔離法構造虛擬支撐，提出了一種改進的基于局部自由響應的子結構損傷識別方法.翁順等[6]通過對子結構的模態解進行組集從而得到整體結構的模態解，從而應用于結構模型的修正與損傷識別.張青霞等[7]提出子結構的虛擬變形方法，利用子結構主要的虛擬變形來模擬損傷，在不重建結構有限元模型情況下，快速計算結構響應，提高了計算效率.

本文進行結構損傷識別時引入子結構的概念，采用Guyan縮聚法[8]先將整體結構劃分為若干子結構，再組成凝聚后的整體剛度矩陣和質量矩陣，在此基礎上進行結構的局部損傷識別；另外，在用功率譜靈敏度進行損傷識別的過程中，采用差分法進行靈敏度分析，解決了參數的偏微分較困難的問題；并采用多個頻率下的功率譜來增加方程個數.通過以上方法，達到較少測點即可進行損傷識別的目的，提高了計算效率，并通過數值算例驗證了方法的有效性.

1 差分法用于功率譜靈敏度分析

1.1 有限元方程與響應功率譜

多自由度結構受迫振動有限元方程為

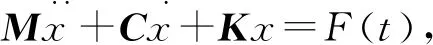
(1)

其中，M為質量矩陣,C為阻尼矩陣,K為剛度矩陣.阻尼矩陣采用Raleigh阻尼模型

C=α1M+α2K.

(2)

結構在受地震隨機激勵、風譜激勵等多點完全相干平穩激勵的情形下，在頻域范圍內求解結構平穩隨機響應的公式如下[9]：

S=H*SffHT,

(3)

其中，Sff為激勵譜矩陣，H*、HT分別為頻響函數矩陣的共軛和轉置，S為待求的響應譜矩陣.

1.2 靈敏度矩陣的求取

基于靈敏度的結構損傷識別法，首先要得到結構模態參數或結構的動力響應對結構物理參數的靈敏度矩陣，再根據結構損傷前后的模態參數變化或動力響應的變化來求取結構物理參數的變化[10].

靈敏度在理論上是一個導數，如結構的響應功率譜(動力響應)對結構單元面積(結構參數)的靈敏度為?S/?A，對于自變量較少，矩陣維數較少的情況下，比較容易獲得函數的導數；但是對于單元數量較多的復雜結構，直接采用導數方法求取靈敏度是比較困難的,有時甚至是不可微的[11].

設結構的單元損傷參數為A，假定結構有m個單元，n個自由度，假定第i個單元發生損傷，則取一個極小的損傷量ΔA，發生損傷后的單元參數矩陣為

A(I)=[A01…A0i+ΔA…A0m]T.

(4)

在損傷量為ΔA的情況下，功率譜變化矩陣

(5)

響應功率譜ΔS對損傷參數A的靈敏度矩陣如式(6)所示.

(6)

其中ω代表功率譜函數的頻率，Sdij為損傷后的功率譜函數.上式為第i個單元損傷時的靈敏度矩陣，由于不能確定結構損傷的具體情況，即單元發生損傷的位置與數量，因此應當將功率譜矩陣中的所有元素分別對所有的單元損傷參數進行差分計算，為了使矩陣能夠表達成一個方程組的形式，將n行n列的靈敏度矩陣寫成一個n*n行一列的矩陣，即

(7)

(8)

(9)

1.3 超靜定方程組的改進

在實際工程中，通過測量結構自由度功率譜響應來進行結構損傷檢測時，通常是選擇結構的部分測點測量，而不是將所有自由度一一測量，在這種情況下，式(9)所表示的超靜定方程組的方程個數將會減少，當方程個數少于未知數時，將會難以求解或者誤差很大.為了解決上述問題，本文采用功率譜的多個頻點來增加方程的個數(但并不增加實驗的次數)，可以通過測量幾個自由度的響應，選取不同頻率下的功率譜值，組成功率譜矩陣和功率譜變化矩陣，并求靈敏度矩陣,組成新的方程組，通過對其求解可得到損傷前后的結構損傷參數.

在本文的框架模型的數值模擬中，選取了4個自由度的響應，比如選擇S11、S12、S13和S144個響應時，然后選擇10個不同頻率下的功率譜對損傷參數求取靈敏度矩陣，組成的方程組如式(10).

(10)

通過由式(3)計算的結構損傷前后響應功率譜，組成功率譜矩陣，并計算得到式(8)的靈敏度矩陣，代入并求解方程組(10)，即可將結構損傷參數識別出來.

1.4 損傷參數識別的迭代過程

當激勵譜以及結構模型損傷前后測量的響應功率譜已知時，可以通過迭代的方法來識別結構損傷參數，用一條曲線來近似模擬迭代的過程(圖1).

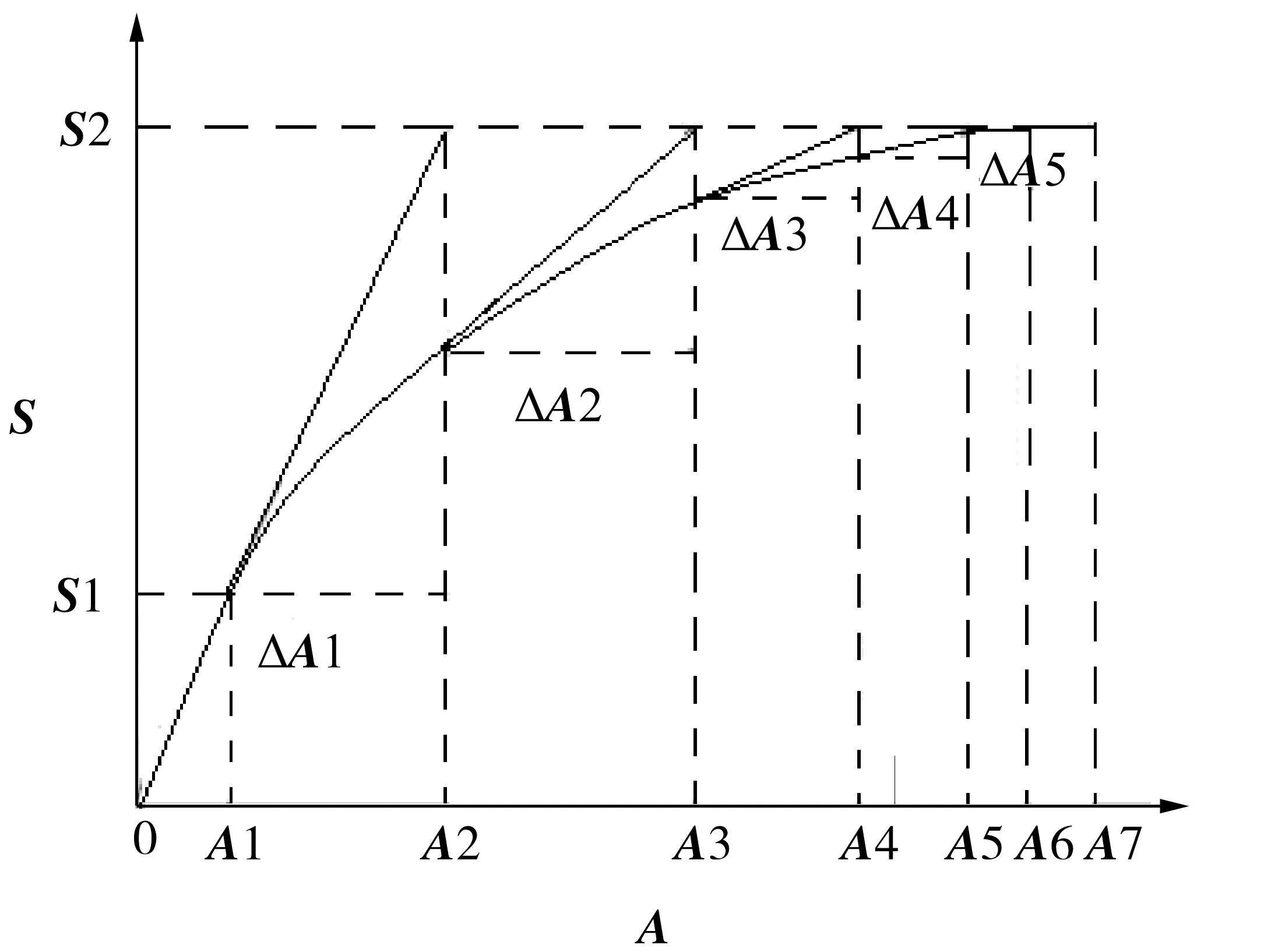
圖1 功率譜函數迭代示意Fig.1 Iterative schematic diagram of power spectral function

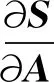
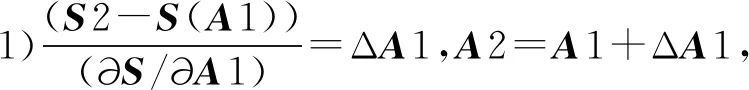
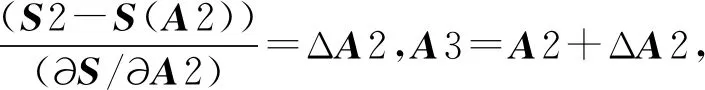
3)S(A3)與S2并不相等，重復以上步驟反復迭代直至得到A(i+1)和S2-S(A(i+1))，當S2-S(A(i+1))的值到達設定的允許值，即A無限接近結構實際損傷后的面積時，迭代結束.最后采用最小二乘法求解超靜定方程組.

2 子結構的Guyan縮聚法

在實際的結構損傷識別問題中, 通過實驗測量的振型通常是不完整的,當發生實測自由度數少于結構有限元模型自由度數的問題時,可以采用模型縮聚方法[12].

首先將整體結構劃分為若干個子結構，對子結構進行模態特性分析，通過實施坐標凝聚，保留部分低階模態，最后達到減少整體結構動力分析自由度的目的.

子結構的Guyan縮聚方法如下：

選擇對接界面自由度為主坐標，用B表示；需要縮減的內部自由度為副坐標，用I表示,則子結構的運動方程為

(11)

忽略對接界面的慣性力，得到子結構的Guyan縮聚變換

(12)

其中，轉換矩陣

(13)

縮聚后的子結構剛度矩陣和質量矩陣為

(14)

(15)

因此，子結構經Guyan縮聚后的運動方程為

(16)

在縮聚前結構的分析自由度為(nI+nB)，通過劃分子結構并進行以上的縮聚，自由度縮減為nB，將縮聚后的子結構和未縮聚的子結構通過“對號入座”的方式組裝，即可得到結構整體的動力學方程.

3 數值算例

3.1 整體結構的縮聚

圖2為三層兩跨的剛架，材料參數彈性模量E=2.06×1011Pa，密度ρ=7 800 kg/m3，截面長寬分別為0.031 m、0.008 m，每個單元長度均為0.28 m.該模型有15個單元，12個節點，36個自由度.

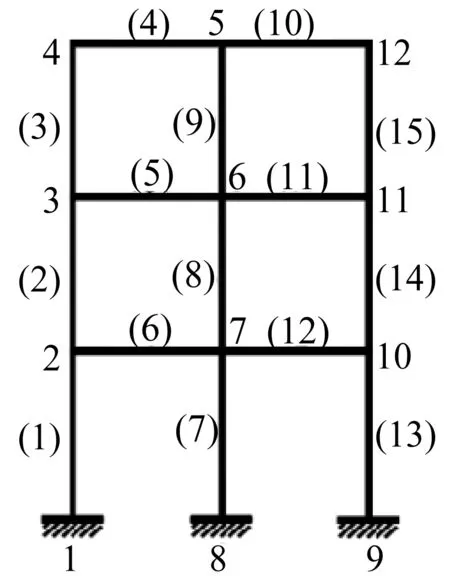
圖2 整體結構Fig.2 monolithic construction

建模時，采用一致質量矩陣，比例阻尼系數α1、α2分別為0.000 5、0.000 1(對于數值模擬，阻尼比的取值對損傷識別結果影響較小), 用ANSYS(有限元建模軟件)和MATLAB(有限元編程軟件)對結構進行模態分析得到整體結構的前5階頻率.在劃分子結構時，子結構劃分不但要有利于各子結構的動態分析和整體的動力綜合，更要盡量兼顧到實際結構加工裝配過程中各部件的“天然”組合狀態，如按實際結構的裝配關系和幾個形狀的相對獨立性劃分；盡可能使各子結構的自由度數相近，避免剛度矩陣或質量矩陣的階數相差懸殊；盡可能按同樣的幾何關系和邊界條件劃分，以減少各子結構特征值的計算次數等[13].因此將模型劃分子結構如下圖3、4所示.其中子結構1中節點5、6、7的自由度為界面自由度，節點2、3、4的自由度為內部自由度.

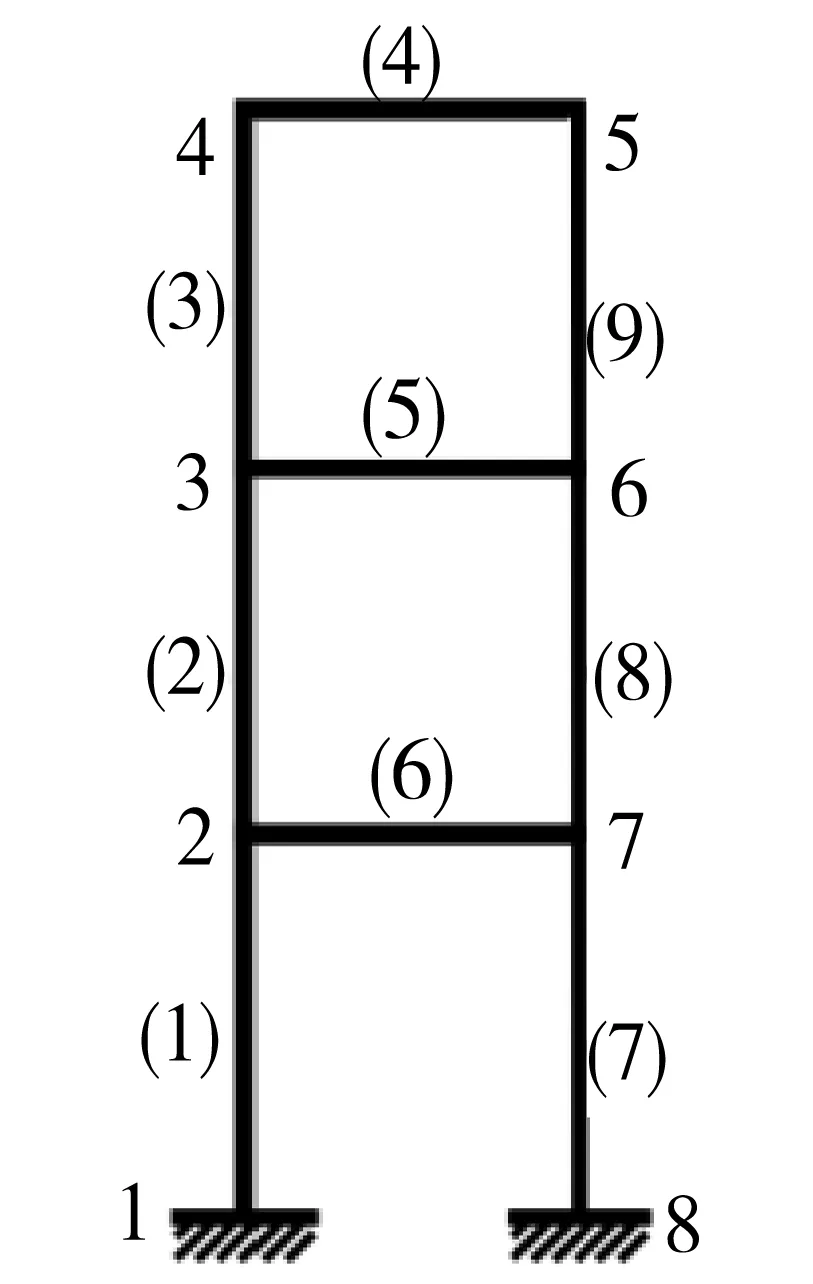
圖3 子結構1Fig.3 Substructure 1

利用上文介紹的Guyan縮聚法將整體結構進行縮聚，將子結構1的內部自由度縮聚掉，經過縮減后的子結構1(只剩余界面自由度)凝聚到子結構2上，形成圖5所示的結構.

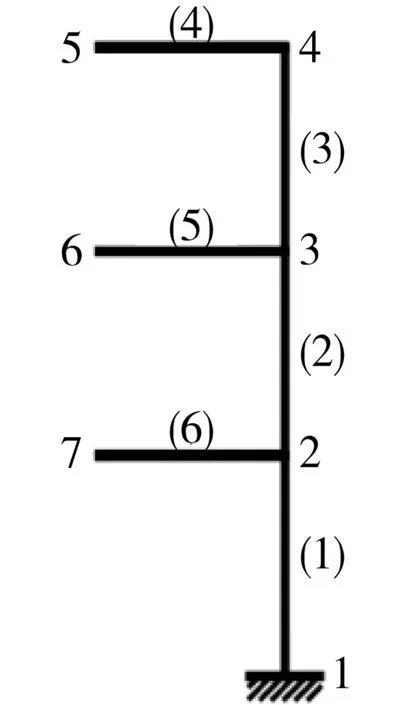
圖4 子結構2Fig.4 Substructure 2

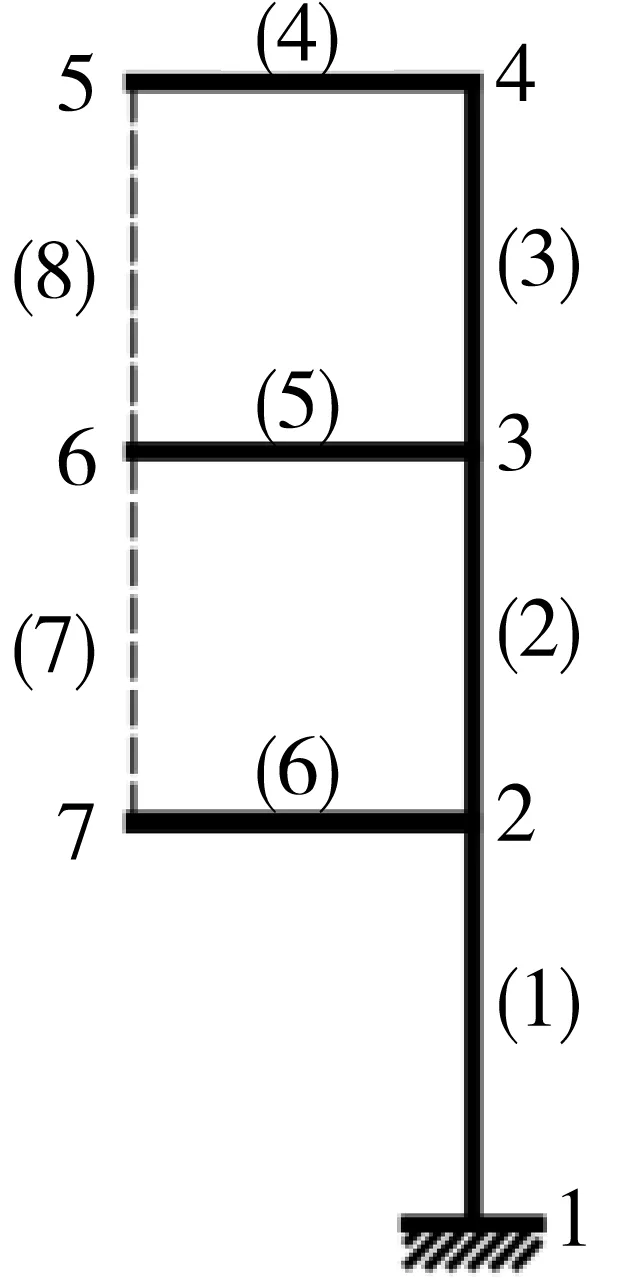
圖5 縮聚后的結構Fig.5 Polycondensed structure

采用MATLAB軟件對縮聚后的模型進行求解運算，得到前5階頻率，并與縮聚前的整體結構的頻率進行比較，結果見表1.

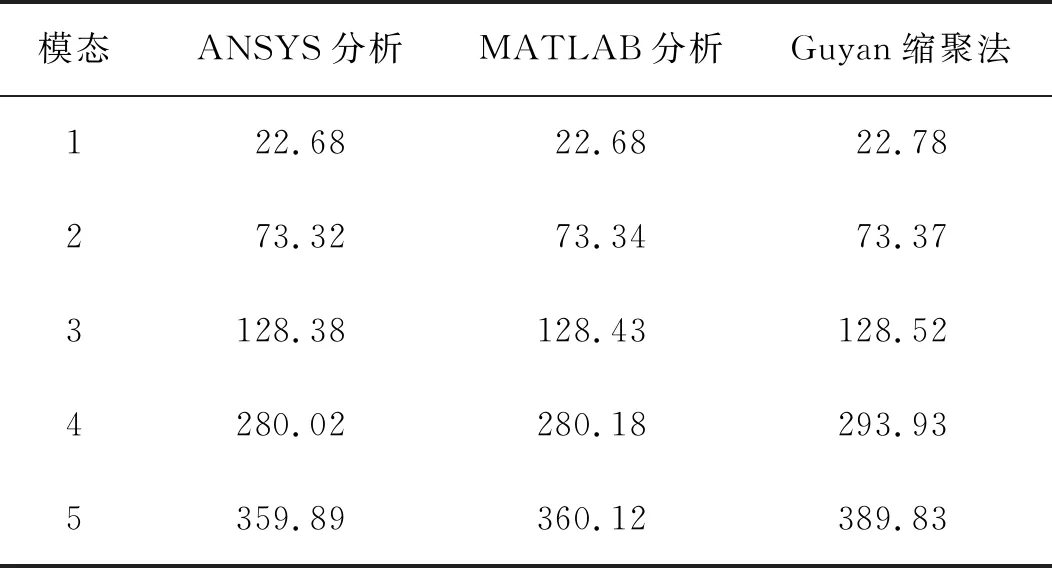
表1 前5階頻率比較

1)觀察表1可知，ANSYS軟件分析結果與MATLAB數值分析計算所得整體結構的前5階固有頻率基本一致.

2)對于Guyan縮聚法得到的結構，前3階頻率與原結構基本一致，由于被縮聚的內部自由度質量較大，隨著頻率升高，精度逐漸降低.

3.2 運用功率譜靈敏度分析法對縮聚結構的損傷識別

基于Guyan縮聚后的質量矩陣、剛度矩陣來求取結構的功率譜函數，進而采用差分法得到對損傷參數的靈敏度矩陣，并代入方程組(10)求解.假定子結構2各節點處作用一水平向左的平穩激勵，采用功率譜曲線峰值點的左右兩邊等差取值選取頻率.

3.2.1 單一損傷檢測

采用減少單元面積的方法模擬損傷，首先進行單一損傷研究，假設縮聚結構的③號單元(即整體結構的?號單元)損傷29.43%，經過25次迭代，結果如圖6所示.

圖6表明能夠成功檢測出結構的單一局部損傷，其檢測誤差為0.008%，其他未損傷單元檢測的最大誤差為3.58%.

圖6 單一損傷檢測Fig.6 Identification of a single damage

3.2.2 多損傷檢測

假設縮聚后模型的單元③、⑤、⑥(即整體結構的?、?、?號單元)分別損傷29.43%、22.40%、17.26%，經過35次迭代，損傷檢測結果如圖7所示.

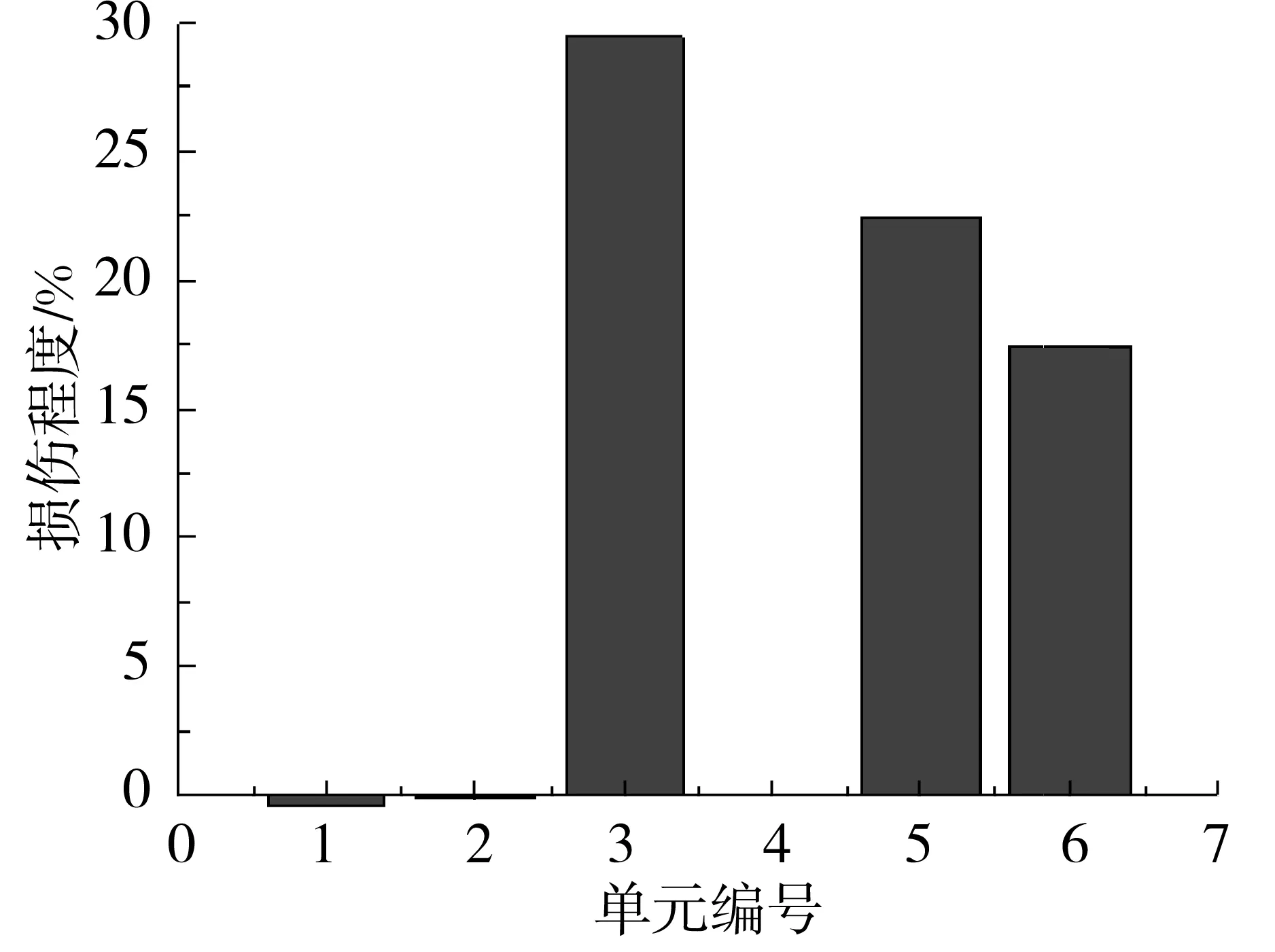
圖7 多損傷檢測Fig.7 Identification of multiple damages

圖7表明能夠檢測出結構多個位置的損傷，最大誤差為1.04%，其他未發生損傷單元檢測的最大誤差為0.39%.

4 結論

本文提出利用差分法進行靈敏度分析，避免了偏微分計算，并采用選取功率譜函數和頻率的方法達到了使用少量傳感器測量響應功率譜，就能較準確檢測出結構單一、多個位置局部損傷的目的.同時，通過子結構的Guyan縮聚大幅度縮減結構自由度，提高了計算效率.研究表明該方法具有良好的應用前景，但是,在實際的工程運用中，對噪聲的影響以及系統進入非線性狀態的損傷識別等問題有待深入研究.