AD-rfMRI圖像的基于改進EDC的獨立分量數目估計
鄭偉,王軒,姚紀智,劉帥奇,張曉丹,馬澤鵬
(1.河北大學 電子信息工程學院,河北 保定 071002;2.河北省數字醫療工程重點實驗室, 河北 保定 071002; 3.河北省機器視覺工程技術研究中心, 河北 保定 071002;4.河北大學附屬醫院CT-MRI診斷科, 河北 保定 071000)
功能性磁共振成像(functional magnetic resonance imaging,fMRI)和彌散張量成像等成像方式作為一種應用于活體的、非侵入式、無損傷的功能成像方式,時間和空間分辨率相對較高,是目前實現阿爾茨海默病(AD)早期診斷的重要成像方式[1-2]. 而基于fMRI的功能連接可以反映腦區之間是否相關以及相關性的大小,從而反映AD患者早期及病程發展過程中腦區之間相關性的變化規律,因此具有更好的研究前景.靜息態功能磁共振成像(resting state fMRI,rfMRI)不需要額外刺激,干擾因素較少,操作簡單而且容易實現,可重復性較高. 2017年,Zhang等[1]掃描了96名受試者的rfMRI圖像,采用獨立分量分析將丘腦分成10個獨立分量后,通過聚類將獨立分量劃分成不同的功能簇,每個簇對應唯一的一個時間序列,通過計算簇時間序列之間的相關系數研究丘腦的功能連接性,結果表明,獨立分量分析與聚類結合對腦區的功能連接分析優于基于種子區的分析方法. 2018年,劉怡秋等[3]將半高全寬值為6 mm的高斯核用于對AD患者的rfMRI圖像進行空間平滑,計算自動解剖標簽模板(AAL)中116個腦區時間序列之間的相關性,并通過單因素方差分析,偽發現率(false discovery rate,FDR)校正以及雙樣本t檢驗比較AD病程發展過程中受試者的功能連接變化. 鄭偉等[4]等針對不同年齡段女性患者靜息態功能磁共振成像,采用獨立分量分析及聚類等方法進行盲源分離和穩定性分析,通過統計檢驗及組間對比研究女性患者各腦區之間的連接關系及其強弱,進而判斷功能連接差異,為女性AD患者臨床前期診斷提供參考. 2019年,馬文潔等[5]對rfMRI圖像進行時間層校正、頭動校正、空間歸一化以及去線性趨勢、濾波后,基于種子點選擇默認模式網絡與背側注意網絡,并將相關系數用于計算功能網絡時間序列之間的相關性,從而研究AD患者感興趣區域的功能連接異常,為探尋AD的發病機制和發病規律提供支持. 基于負熵的快速獨立分量分析(fast independent component analysis algorithm based on negative entropy,NE-FastICA)算法收斂速度快,分離精度高,在腦功能連接分析中普遍使用, 但存在分離之前獨立分量數目的過估計問題. 本文提出對實現獨立分量數目估計的有效檢測準則(effective detection criteria,EDC)進行改進,將對數函數用于懲罰函數,并與黃金分割法確定參數γ相結合,本文稱其為OIEDC2,改進后解決了分量數目的過估計問題,給出了合理的估計數目.
1 受試者fMRI分組情況
本文將65~80歲的89名女性AD患者的rfMRI圖像(來源于ADNI數據庫https://ida.loni.usc.edu/login.jsp?project=ADNI)作為研究對象,按照疾病的發展階段分為4組,對照組受試者(subjects of normal control,fsub_CN)17人、早期輕度認知障礙受試者(subjects of early mild cognitive impairment,fsub_EMCI)23人、晚期輕度認知障礙受試者(subjects of late mild cognitive impairment,fsub_LMCI)19人和AD受試者(subjects of AD,fsub_AD)30人的rfMRI圖像,受試者情況如表1所示. rfMRI的相關參數如表2所示.

表1 受試者基本信息

表2 圖像基本參數
2 基于EDC的獨立分量數目估計
基于信息理論準則的估計方法主要包括貝葉斯信息準則(bayesian information criterion,BIC)[6]、赤池信息準則(akaike’s information criterion,AIC)[7]、最小描述長度(minimum description length,MDL)[8]、kullback-leibler信息論準則(kullback-leibler information criterion,KIC)[9]和EDC[10],這些信息理論準則通過最小化目標函數實現對獨立分量數目的自適應估計,EDC估計如式(1)所示.
(1)
其中,-2L(x(n)|θk)可衡量EDC模型對數據的擬合程度,η(θk,N)CN為懲罰函數項,γ∈[0.1,1]為調整懲罰項的參數,可以調整估計性能,懲罰項中CN是可變的.2種不同懲罰函數下的EDC分別用EDC1和EDC2表示,如式(2)和式(3)所示.
EDC1(k)=-2L(x(n)|θk)+η(θk,N)(NlgN)γ,γ∈[0.1,1]
,
(2)
EDC2(k)=-2L(x(n)|θk)+η(θk,N)Nγ,γ∈[0.1,1]
.
(3)
信息理論準則用于估計獨立分量數目時,若對rfMRI估計的獨立分量數目在20~40,表明估計結果較合理[10]. 將AIC、KIC、BIC、MDL、EDC1以及EDC2用于估計4組受試者的獨立分量數目,結果如圖1所示.

圖1 不同準則下對4組受試者的估計結果對比Fig.1 Comparison of estimation results of four groups of subjects based on different criterion
由圖1可知,AIC、KIC、BIC和MDL的估計性能接近,且在fsub_EMCI、fsub_LMCI和fsub_AD中均存在嚴重的過估計問題;EDC1和EDC2對每組受試者估計的獨立分量數目相對較少,雖然EDC2存在過估計問題,但估計性能優于EDC1.
EDC2的過估計問題是由于其懲罰函數和γ值的非最優性導致的,本文提出將對數函數引入懲罰函數,并結合黃金分割法確定γ最優值的EDC2改進策略.
3 改進懲罰函數的EDC2及實驗對比分析
3.1 基于對數懲罰函數的改進EDC2
式(1)中的懲罰函數項η(θk,N)CN的CN項是可變的,滿足式(4)所示的條件.
(4)
其中,N為rfMRI的混合信號數,即體素數.
由式(3)可知,EDC2中CN=Nγ對γ求一階導數的結果如式(5)所示.
CN=NγlnN,γ∈[0.1,1]
,
(5)
其中,N較大時,隨著γ值增大,CN的變化率較快,EDC2估計的獨立分量數減小的較快,容易造成低估計;γ值減小時,EDC2估計的獨立分量數增加的較快,容易造成過估計.
由于對數函數在自變量較大時變化趨勢較為平緩,本文將對數函數引入懲罰函數項,用于改進EDC2,稱為改進有效檢測準則(improvement of effective detection criteria,IEDC2),如式(6)所示.
CIEDC2=[loga(N)]γ,γ∈[0.1,1]
,
(6)
其中,a為對數函數的底數,可以取2、e和10.
改進的懲罰函數項需滿足式(4),下面將給出證明:
首先計算關于式(6)的2個極限,CIEDC2與N比值的極限如式(7)所示.
(7)
函數y=loga(N)是一個單調遞增函數,相同N下,γ=1時CIEDC2達到最大值,由于N→∞時,N達到∞的速度比loga(N)快,式(7)中CIEDC2取最大值時的極限為
(8)
當γ=0.1時CIEDC2達到最小值,N→∞時,N達到∞的速度比[loga(N)]0.1快,式(7)中CIEDC2取最小值時的極限如式(9)所示.
(9)
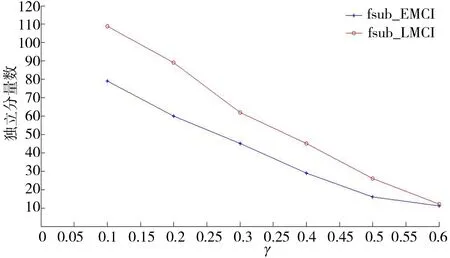
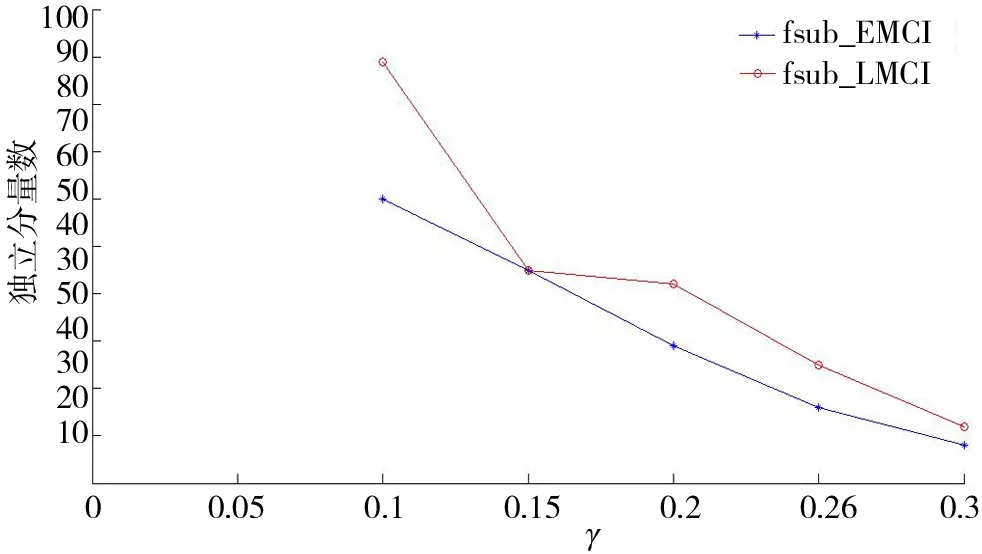
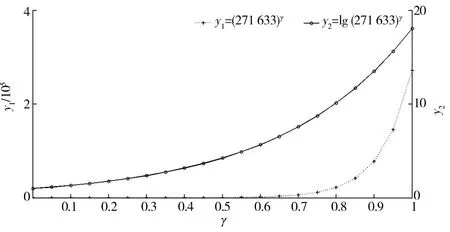
CIEDC2與CIEDC2max、CIEDC2min之間滿足CIEDC2min (10) CIEDC2與lglgN比值的極限如式(11)所示. (11) 對數函數換底公式如式(12)所示. (12) 將式(12)代入式(11),結果如式(13)所示. (13) 若令lgN=u,則式(13)可轉化為式(14). (14) 其中(lga)γ為與u無關的常數,則式(14)可寫成式(15). (15) 當u→∞時,指數函數達到∞的速度比對數函數快,因此式(11)的推導結果為 (16) 由式(10)、式(16)可知,式(6)作為懲罰函數時滿足式(4)的條件,因此將對數函數引入EDC2以改進懲罰函數項,是合理的. 式(6)中,底數a不同時,對數函數變化趨勢不同,a取2時記為f1=log2x,a取e時記為f2=lnx,a取10時記為f3=lgx,3種常用對數函數變化趨勢對比如圖2所示. 圖2 3種函數變化趨勢對比Fig.2 Comparison of three logarithmic functions 由圖2可知,底數越大,函數值越小,3個函數中f3的值最小,反映為自變量較大時f3的變化趨勢較平穩,本文將f3用于IEDC2懲罰函數得式(17),則IEDC2估計可表示為式(18). CIEDC2=η(θk,N)(lgN),γ∈[0.1,1]. (17) IEDC2(k)=-2L(x(n)|θk)+η(θk,N)(lgN),γ∈[0.1,1] . (18) 為了衡量IEDC2改進后的估計性能,以fsub_EMCI、fsub_LMCI 2組受試者為例,將EDC2、IEDC2在不同γ值下的估計結果進行對比. EDC2的估計結果如圖3a所示,圖3a中EDC2對2組受試者的估計結果存在過估計問題;γ值越小,估計的獨立分量數目越多,γ值越大,估計的獨立分量數目越少,不同γ參數下,EDC2對fsub_EMCI估計的獨立分量數目有3個值為20~40,對fsub_LMCI估計的獨立分量數目有4個值為20~40,選擇的獨立分量數目不同會導致盲源分離結果也不同. IEDC2的估計結果如圖3b所示,2組受試者的估計結果雖然在參數γ較小時仍存在過估計問題,但與圖3(a)相比,相同γ值下,IEDC2估計的獨立分量數目明顯下降,表明IEDC2改善了過估計問題;不同參數γ下,IEDC2對fsub_EMCI、fsub_LMCI估計的獨立分量數目均只有1個值在20~40,表明IEDC2避免了因獨立分量數目不同導致的盲源分離結果出現差異,提高了估計結果準確性. a.EDC2;b.IEDC2. EDC2的估計性能除了受到不同懲罰函數的影響外,還與參數γ有關,γ越大EDC2估計的獨立分量數越少,越容易造成低估計;γ越小,EDC2估計的獨立分量數越多,越容易造成過估計. 將EDC2中的CN記為y1=Nγ=271 633γ,IEDC2中的CN記為y2=[lg(271 633)]γ,則y1、y2隨γ值變化的趨勢如圖4所示. 圖4 y1和y2隨γ值的變化趨勢對比Fig.4 Comparison of the change trend of y1 and y2 with γ values 圖4中橫軸為參數γ,左邊縱軸對應y1=271 633γ的函數值,右邊縱軸對應y2=[lg(271 633)]γ的函數值,對比可知,體素數N一定時,相同γ值下,y1函數值的變化率快,表現為γ值增加時,EDC2估計的獨立分量數減小較快,容易造成低估計;γ值減小時,EDC2估計的獨立分量數增加較快,容易造成過估計. 本文針對不同γ值下EDC2對4組受試者的估計結果存在過估計問題提出改進,在IEDC2懲罰函數的基礎上,利用黃金分割法確定γ的最優值,改善IEDC2的估計性能.將黃金分割法用于確定最優γ值優化改進有效檢測準則,本文簡稱為OIEDC2. 黃金分割法每次將搜索區間縮小0.618倍,根據精度要求以0.618n的縮減速率尋找最優點.γ值的范圍是確定的記為[a,b],黃金分割法首先確定2個初始實驗點r1和r2,其中實驗點r1由式(19)確定.實驗點r2由式(20)確定. r1=a+0.618×(b-a). (19) r2=a+b-r1=b-0.618×(b-a) . (20) 黃金分割法第一次確定2個實驗點,之后通過對比、迭代依次確定下一個實驗點,同時更新變量區間,縮小變量范圍,最終通過評價函數確定最優點.黃金分割法通過不斷更新γ的區間最終確定參數γ的最優值,直至IEDC2(γ)滿足式(21).將滿足式(21)的γ稱為參數γ的最優值,記為γbest.將γbest用于式(18)可得OIEDC2估計如式(22)所示. 20≤IEDC2(γ)≤40 . (21) OIEDC2(k)=2L(x(n)|θk)+η(ηk,N)[lgN]γbest. (22) 為了衡量OIEDC2改進后的估計性能,將EDC2、IEDC2和OIEDC2分別用于估計4組受試者的獨立分量數目,結果如表3所示. 表3 EDC2、IEDC2和OIEDC2的估計結果 由表3可知,EDC2對4組受試者的估計結果均存在不同程度的過估計問題;IEDC2對fsub_CN估計的獨立分量數在20~40,估計結果較合理,對其余3組受試者雖然存在不同程度的過估計問題,但對fsub_LMCI估計的獨立分量數與40較接近,估計結果比EDC2好,對fsub_EMCI和fsub_AD估計的獨立分量數比EDC2低,表明與EDC2相比,IEDC2的估計性能有所改善;OIEDC2對4組受試者估計的獨立分量數目均處于20~40,估計結果都比較合理,因此本文改進后的OIEDC2避免了過估計問題,實驗結果比改進前的EDC2要好. 本文對基于EDC2的獨立分量數目估計方法進行改進.將對數函數引入EDC2的懲罰函數項,稱為IEDC2,將黃金分割法引入IEDC2確定最優參數γ,稱為OIEDC2,并將結果進行對比分析,衡量EDC2改進前后的估計性能.實驗結果表明,本文方法有效解決了4組受試者獨立分量數目的過估計問題,估計結果更合理.為后續的基于獨立分量的盲源分離,獨立分量選擇,感興趣區域功能連接計算,實現4組受試者的功能連接分析,并通過統計檢驗獲取隨疾病發展進程感興趣區域功能連接的變化規律,進而為尋找導致功能連接變化的內外部因素以及性別與AD發病的關系,即為AD發病機制的研究奠定基礎.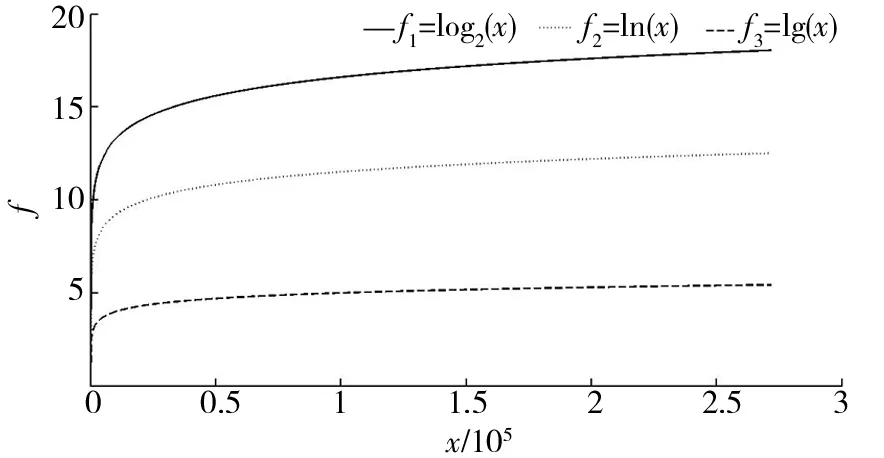
3.2 IEDC2實驗結果及對比分析
4 基于黃金分割法的γ值確定
5 實驗結果及對比分析

6 結論

