干燥物系的特征函數及其理論解

李長友

（華南農業大學南方農業機械與裝備關鍵技術教育部重點實驗室，廣州 510642）

0 引 言

干燥是動量、熱量、水分3種傳遞同時作用的過程，動量傳遞可由牛頓黏性定律描述；熱量傳遞可由傅里葉定律描述，而水分傳遞稱為擴散，可以由費克定律描述。3個定律客觀地從理論上描述了物系單一行為的傳遞現象，依此為基礎，人們把水分遷移假設成連續介質流動，基于時間和空間的連續函數，采用歐拉方程、拉格朗日方程、體積平法等，圍繞表征物系性質和過程特征的進行了大量的模型試驗理論研究，由試驗數據，給出了針對特定物系多種形式的計算模型[1-3]。由于流動過程不存在嚴格的牛頓流[4]，依賴濃度的擴散系數沒有數學解[5]，熱傳遞過程物性動態變化的內部因素與外部條件雙向作用，很難揭示熱傳遞系數的變化規律。3個定率應用時，除必須滿足各自的單值性條件外、還要盡可能滿足其幾何條件、物理條件、時間條件和邊界條件等。在模型求解時，必須把過程的綜合因素歸結為常系數才能進行，因此，不能保證積分結果與實際完全一致。基于擴散動力學建立的物料干燥模型，存在活化能、指前因子和過程指數難以定量等問題[6]，如何獲得干燥過程的分析解是長期以來干燥理論研究的重要命題。

干燥是物料水分蒸發的自發過程，干燥動力變化范圍在水的飽和蒸汽壓與外部的水蒸汽分壓力之間。無論何種物料，在何種外部約束條件下，干燥的動力都是源自于水的飽和蒸汽壓，它是汽化溫度的單值函數[7]。干燥所能到達的極限，是物料水分活度在數值上等于外部介質的相對濕度的平衡含水率狀態點，而狀態變化取決于干燥的廣度和強度，廣度與去除的水分量成正比[8]，在數值上等于物料含水率與其平衡含水率之差；強度用干燥速率來表征。為了揭示干燥狀態變化規律及其發生的機理，研究人員針對不同物料，建立了干燥速率、升溫速率、質構變化（收縮與變形）規律、質量與品質的變化等多種干燥模型[9-10]。按照唯象理論和體積平均理論[11]，建立擴散微分方程[12-13]，基于抽象的不可逆熱力學函數來表達水分擴散現象，預測干燥速率，確定干燥時間，分析實際過程，指導工藝設計和優化過程控制[14-15]，但沒有揭示模型中計算系數的物理意義[16-17]。

基于質量、能量守恒定律和不可逆熱力學原理，Philip和Devries把物料內部質量傳遞區分為毛細管流動和蒸汽擴散運動2種情況，基于溫度、濃度和壓力3種勢場，建立了各種干燥微分方程組[18-22]，基于孔道網絡模型的模擬手段[23-24]解析干燥過程并展開了一系列擴散模型及其計算系數的研究[25]，在假設蒸發面由物料外表面向內退縮，蒸發面積逐步減小等條件下，解析降速干燥過程[26-28]。以汽化界面為分界面，把物料干燥狀態，簡化成界面內部為濕區，界面外部為完全處于平衡態的干區，并認為濕區的相對濕度為100%，且水分汽化只發生在干區和濕區的交界面上，給出了諸多解析特定物料干燥過程的擴散模型。由于干燥是在濕、熱和動態變化的物性參數等多種因素作用下的非線性自發過程，伴隨去水，物料自身的物理性狀實時改變并發生復雜的理化、生化反應，體積收縮、質構變化會引起空隙、迂曲度改變，導致水分傳遞路徑及強度發生改變，都使實際過程與理想化的分界面擴散不一致[28-32]，這是把實際過程歸結成常系數擴散，建立模型時的共同缺陷[33-35]。

影響干燥現象的因素繁多，但一切因素綜合作用的結果，完全反映在水分蒸發，而能否蒸發要取決于物料水分的活度。活度是溫度、物料含水率的函數。近年，筆者以水分活度變化為物料干燥狀態的統一特征，明確了干燥是水分汽化對外做功的自發過程，汽化現象的標志是呈現功的輸出，這個功源自于物系的自由能，基于自由能變化，給出了物料水分的結合能解析式[36]，得到了物料水分汽化潛熱系數的數學解[37-38]。在此基礎上，本文以水分活度為物料干燥的統一特征，以自由能傳遞和轉換為統一尺度，按照能量平衡原理，對應外部約束條件，建立具有普遍意義的干燥物系特征函數并給出理論解，揭示干燥物系的機理函數。

1 干燥物系的過程特征

1.1 干燥特性

按照水分與物料的結合形式，可以把干燥區分為非結合和結合水分蒸發兩種情況。非結合水，不受物料的作用，相當于自由液面蒸發，結合水分是存在于物料中的水分，蒸發受物料的影響，作用的結果完全取決于物料自身的物理性質。與其對應的干燥特性如圖 1所示。非結合水的水分活度等于1，蒸發速率取決于外部條件；而結合水與干物質組分間存在結合能，水分活度小于 1且在干燥過程中隨含水率降低而減小，在穩態介質條件下，蒸發速率是物料水分活度的函數。

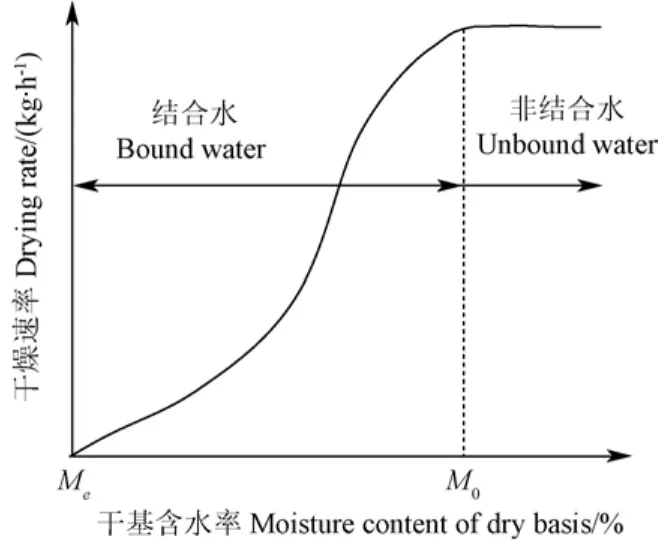
圖1 干燥特性曲線Fig.1 Drying characteristic curve

1.2 干燥系統

干燥是濕物料與外部介質，通過邊界進行能量和質量傳遞與轉換的開口系統。在此，用符號pe和p分別表示介質和物料中的水蒸汽分壓，用ps、pv和φ分別表示飽和蒸汽壓、汽化后的水蒸汽在物料內部的分壓力和水分活度，用T和μ分別表示汽化溫度和物料水分的結合能。簡化的干燥系統如圖2所示。

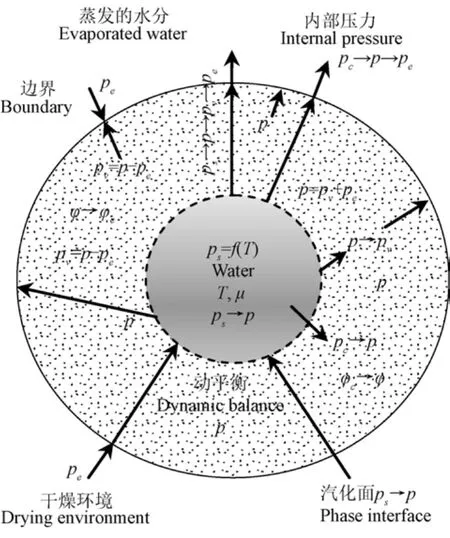
圖2 干燥系統Fig.2 Drying system

1.2.1 系統狀態參數及其變化

物料內部水分蒸發經歷由汽化面蒸發、擴散到系統邊界，然后進入介質的過程。在汽化面內部及汽化面上的水蒸汽壓是飽和蒸汽壓ps，ps與物料無關，它是溫度T的單值函數，是水蒸汽的最大動力極限。由于物料水分蒸發受結合能的影響，結合能降低了蒸發面上方的水蒸汽分壓力，使水蒸汽遷出的動力減小，從而在汽化面的上方呈現的壓力是p，轉變的位置發生在汽化面上方，所以，p是水分汽化遷移的動力。

由于氣體壓力波傳播的速度很快，物料含水率的變化速率遠遠小于氣體分子的壓力波傳播速率，所以，當干燥過程中系統外部的水蒸汽分壓力恒定不變，物料內部的水蒸汽分壓力則是經歷無數中間狀態，由初始的水蒸汽分壓力pc→pe的準平衡過程。

當介質中存在水蒸汽分壓力pe時，這個壓力直接作用在系統的內外。那么，汽化份數，在物料內部與介質中的水蒸汽相混合的過程中，則會使其壓力由p狀態變成了pv狀態。變化的幅度則是取決于pe的大小，即pv=p-pe，pv是蒸發份數遷出物料的最終動力。

由此可見，物料蒸發出的水蒸汽狀態變化是的過程的狀態變化發生在汽化面上。的狀態變化過程是由汽化面到系統的邊界，即物料的內表面。遷出物料后，趨向于pe。

當pe=0時，干燥則沒有外部水蒸汽分壓的影響，干燥過程完全取決于物料自身，所以，在pe=0的條件下，便可完整地解析出物料水分的結合能。

由于p的值取決于物料水分的活度，它是一切物料水分的共同屬性。在干燥過程中水分活度隨含水率的降低而減小且是連續變化的。變化的規律體現在水分結合能大小和混合后的pv值。基于水分活度ps→p，和p→pv的壓力狀態變化及其發生的位置和區域，按照水分活度φ=p/ps，即可解析出物料內部的水分活度分布，進而，由實際去水的廣度和任意一個對應水分活度為φ狀態點的去水強度，即可得到實際干燥過程的理論解。

2 水分蒸發自由能平衡方程

2.1 自由能傳遞與轉換理論表達式

干燥現象可以由水分遷移的數量與其遷移勢之積來表達，完全取決于物系的狀態參數，而一切過程只要是取決于熱力狀態參數的能量都全部歸結為焓[7]，所以，無論水以何種形式存在于物料中，也無論干燥的一切機理參數如何變化，干燥現象都可以由狀態函數來表達。因此，在任何條件下，干燥過程的任一狀態點的熱能消耗都可依據該狀態點的焓來計算。基于吉布斯-亥姆赫茲自由能概念，得到1 kg水分定壓汽化過程的熱力學第二定律的數學表達式（1）或式（2）

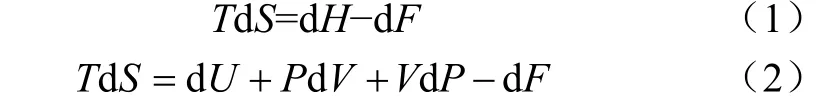
式中T是熱力學溫度，K；S是熵，kJ/K；H是焓，kJ；P是壓力，Pa；V是體積，m3；U是內能，kJ；F是自由能。kJ。

水在自由狀態下定壓汽化時，不產生軸功，式（2）中的VdP項等于 0，于是得到水在自由態定壓過程中的自由能表達式（3）[8,36]。

水在物料中汽化時，結合能降低了蒸發面上方的水蒸汽分壓力，相應地減少了水分的自由能，自由能減少的量在數值上相當于汽化過程所做的技術功（軸功）。此時，式（3）中的VdP項不等于 0，在此，用符號Fg表示汽化份數，汽化時的自由能消耗，得到物料水分，定壓汽化時的自由能消耗表達式（4）。

式中的VdP是克服水分結合能所做的軸功，其值等于遷移勢與質量之積，在數量上，與汽化份數的質量成正比，可由式（5）計算[8,38]

式中的dM是汽化遷移的水分量微元，kg，負號表示遷移的方向沿質量減小的方向。μ是水分的質量遷移勢，kJ/kg，即汽化1 kg水分克服結合能所做的功，在理論上可表達

式中Md是除水分以外的其他組分，在此稱其為絕干物質質量，kg。

由式（1）知，dF=dH?TdS，自由態的水，定壓力汽化時，式（2）中的VdP項等于0，d(PV)=PdV，由于P和V都是狀態參數，源自于系統的熱能，熱能在任何情況下都可以用一個平均過程比熱與其溫差之積來表達，在此，用符號Rpn，表示在[273.15,T]溫度區間，水分汽化，自發流動趨向終態平衡過程中，自由能轉化為單位質量流體溫度變化1 K的熱能平均值，并稱其為水分汽化過程特征常數，kJ/(kg·K)，它的物理意義等同于水分汽化過程的平均定壓比熱，可以由中值定理和壓力函數與其原函數（自由能傳遞和轉換）得到證明。由此，對應定壓汽化條件，得到從物料內部每遷移1 kg水分時，自由能轉化的功，這個功在數值上等同于水同物料的結合能，即dμ=-vdp=RpndT，積分得到解析式（6）[36]。

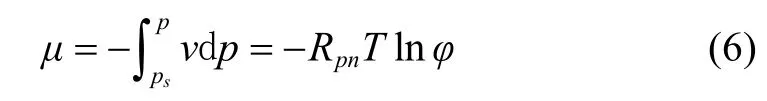
式中φ是水分的活度（小數），Rpn是以三相點為基準，水分汽化溫度[273.15,T] 的區間特征常數，kJ/(kg·K)，p是水蒸汽的分壓力，Pa，ps是飽和蒸汽壓，Pa。

用小寫字母v表示比體積，m3/kg，h表示比焓，kJ/kg，f表示比自由能，kJ/kg，得到1kg水分在自由態和物料中汽化時的自由能消耗微分式（7）和式（8）

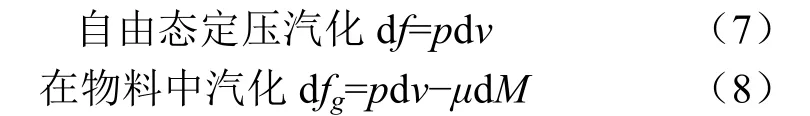
由于同溫度下水蒸汽的比體積遠大于水的比體積，二者相比，水的比體積可以忽略不計，于是，求積得到 1 kg水分在自由態汽化為理想氣體時，消耗的比自由能表達式（9）。

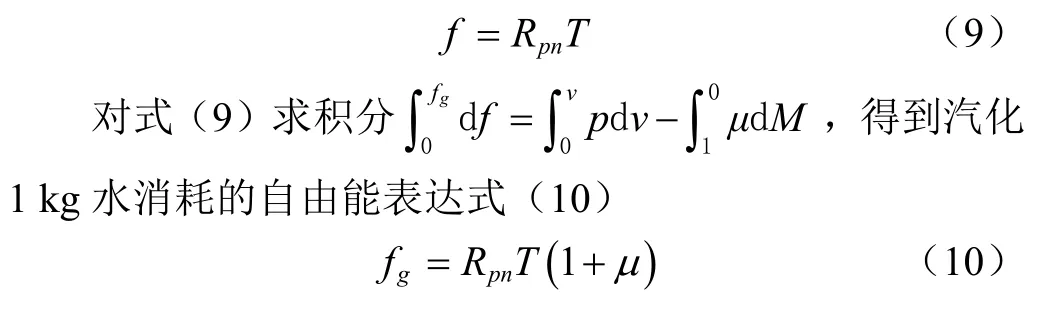
把式（6）代入式（10），得到物料水分汽化時的比自由能消耗表達式（11）

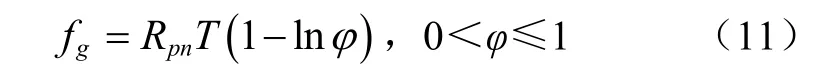
式（11）表明，在確定的溫度區間，水分蒸發的自由能消耗量，是絕對溫度和水分活度的狀態函數，式（11）適合任何物料，具有普遍意義。在此，用符號Cz表示1?lnφ項，并稱其為自由能消耗系數，得到表達式（12）。

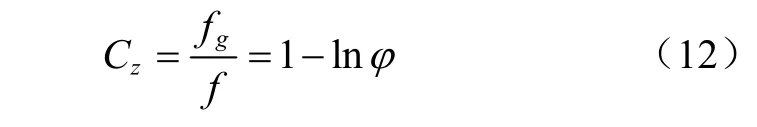
式（12）表明，當水分活度等于 1時，自由能消耗系數等于1，存在水分結合能時水分活度小于1，此時的自由能消耗系數大于1。表征從物料中汽化同樣數量的水分消耗的自由能是自由態時的1?lnφ倍。

2.2 蒸發過程的自由能平衡方程

假設在水分活度等于1時，物料的干基含水率為M0，%。對應介質條件的平衡含水率為Me，%。分別用符號區間上的最大汽化速率和干燥速率，%/h；那么，小的量，則等同于物料約束水分蒸發多消耗的自由能，由此得到式（13）所示的自由能消耗平衡關系式，化簡式（13）得到物料自身固有的干燥速率比狀態函數表達式（14）。

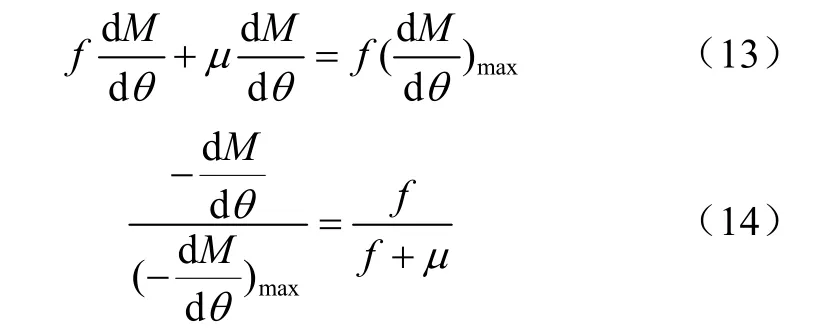
把式（6）和（9）代入式（14），得到干燥速率比狀態函數表達式（15）

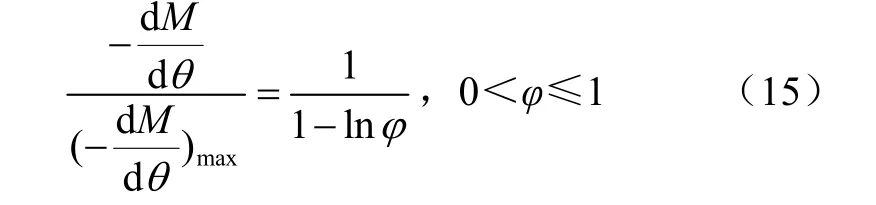
式中θ是干燥時間，h。

式（14）和式（15），表征的是物料經歷準平衡過程所能實現的理論干燥速率。式（15）中的表達的是物料在理想絕干介質中，穩態干燥的情況，是物料自身固有的干燥特征函數之一。

由式（15）可以看出，干燥速率比與成正比，它是在外部介質相對濕度等于 0的條件下得到的，是干燥速率比隨水分活度變化的一般關系式，它是強度量之比等同于質量比。由式（14）知，這個比值又等同于自由能比，所以，無論何種物料，只要其水分活度相同，汽化相同數量的水分克服結合能做功的自由能消耗必然相等。因此，式（15）可以用來評價干燥物系的理論熱耗，但干燥速率與外部介質條件和物料內部含水率分布有關，水分汽化后的運動和狀態變化與外部介質的含濕量有關，在解析實際過程時，應基于圖 2揭示出蒸發份數在相應的外部介質條件下，汽化、混合過程的阻力特征，其自由能消耗要基于式（22）來定量。

2.3 理論干燥速率比變化特征

在外部介質相對濕度等于 0的干燥過程中，任何物料的干燥速率比都是其水分活度的單值函數。那么，對應[1,0）的水分活度變化區間，基于式（15）解析出的干燥速率比隨水分活度的變化規律如圖3所示。

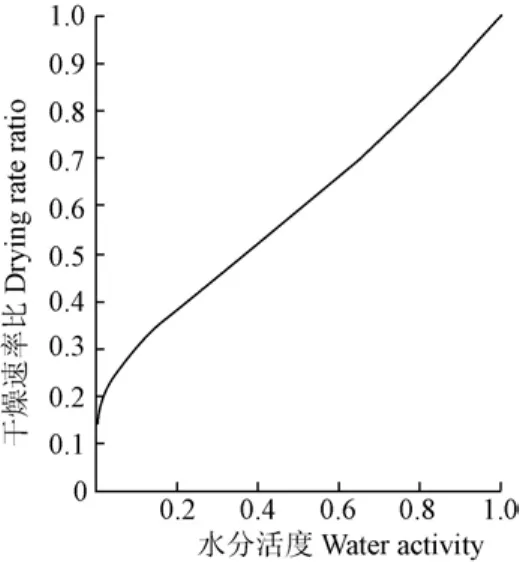
圖3 干燥速率比的變化Fig.3 Change of drying rate ratio

水分活度反映物料水分結合程度和水分遷出時的受阻情況，體現在物料水分遷移受到干物質組分的阻力而消耗的自由能，由圖 3看出水分活度值越高，干燥速率比越大，表明結合程度越低，與干物質間的結合能越小；而水分活度值越低，結合程度越高，與干物質間的結合能越大。在水分活度趨向于0時，干燥速率比也趨向于0時，此時水分活度的微小變動，會引起干燥速率比的較大變化。

2.4 物料水分活度計算式

水分活度取決于物料的含水率和溫度，是物料自身固有的狀態函數之一。在穩態條件下，平衡含水率是物料干燥所能到達的極限，是物料完全回歸環境態時的含水率。針對不同種類的物料，不同國家的研究機構和學者，給出了多種平衡含水率計算式，并稱其為平衡含水率模型[39-42]。

由于平衡含水率可在靜態試驗條件下正確測量，對應不同的物料已有較為精確的計算式。式（16）是國際上普遍采用的平衡含水率模型之一，模型中計算參數如表1所示[37]。

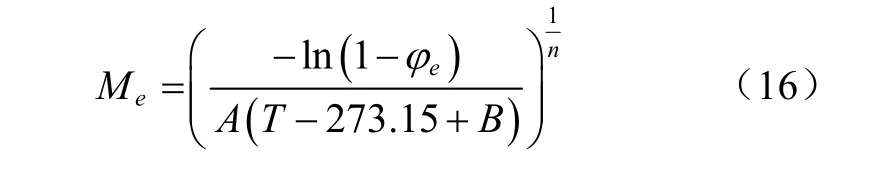
式中A、B、n為計算系數。

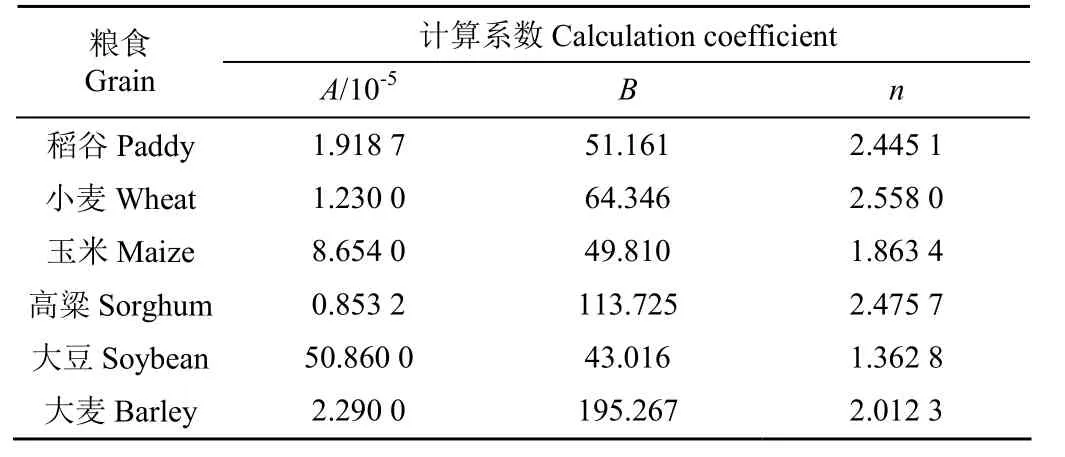
表1 幾種糧食平衡含水率模型中的系數值Table 1 Coefficients in several models of grain equilibrium moisture content

平衡含水率是狀態函數，對于所有物系，在理論上均可表達為Me= [f(T,φ)]e，下標e表示的是相平衡條件，基于式（16），得到干燥介質的平衡相對濕度φe表達式（17）。

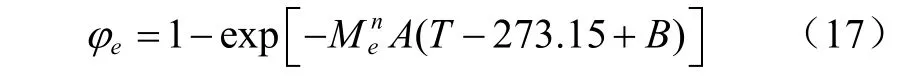
在相平衡條件下，物系中各點的遷移勢均等，質量遷移梯度為0，物料內外的溫度、壓力平衡，各個狀態參數都不隨時間變化，那么，在相平衡條件下，水分活度在數值上則等于介質的相對濕度，其值可以由介質的溫度和相對濕度計算。根據熱力學分析問題的一般方法，將干燥現象看作是從一個平衡狀態趨向另一個平衡狀態的過程。于是，對應物系相平衡過程的物料水分活度就可表達為式（18）。

式中T是物料溫度，K，φ是水分活度，M是含水率，%。式（17）和式（18）中的 2個自變量分別是物料含水率和溫度，這2個參數都是干燥物系的狀態參數，但式（17）和式（18）的物理意義不同，物料水分活度是自身的狀態參數，是取決于物料溫度和含水率的狀態函數，而介質的相對濕度是介質溫度和濕含量的狀態函數。

2.5 單位自由能及最大干燥速率比變化規律

單位自由能消耗是指從物料中每蒸發1 kg水，物料消耗內能使水蒸汽運動而具有對外做功能力的那部分能量，單位是kJ/kg。在理論上，它是每蒸發1 kg水，可向外輸出的技術功。由式（1）或式（2）知，它是內能轉化的技術功。基于式（11）、式（12），式（18）和式（15）解析的不同溫度條件下，小麥干燥狀態函數的變化規律如圖4所示。

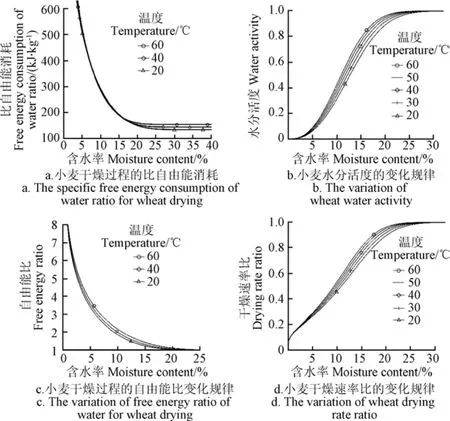
圖4 小麥干燥狀態函數變化規律Fig.4 Change rule of drying state function of Wheat

水分汽化時的單位自由能消耗隨含水率的變化規律如圖4a所示，水分活度隨含水率的變化如圖4b所示，自由能比隨含水率變化如圖4c所示，干燥速率比隨含水率的變化如圖4d所示。

從圖4a看出，小麥降速干燥過程的單位自由能消耗隨含水率的降低而增大，且含水率越低增大的幅度越大，其影響明顯高于溫度的影響，但當含水率高于25%以后，在不同干燥溫度條件下的自由能變化與溫度間的關系趨于確定的常數，且是溫度越高，其值越大，此時的物料水分的自由能變化可以看作是溫度的單值函數，水分的汽化過程則等同于自由液面蒸發。

自由能比無量綱，是一切物料狀態變化的共同屬性。在水分活度等于1時，自由能比等于1，存在水分結合能時，水分活度小于1，自由能比大于1且隨水分活度的減小而非線性增大。

無論何種干燥工藝系統，物料的干燥過程都必然存在對應其降水期間上的最大干燥速率狀態點，在相同的介質條件下，該狀態點必然是水分活度的最大點。由式（11）知，RpnT在對應的溫度區間[273.15,T]上是常數，所以，以三相點為基準點，在任意一個溫度區間內，干燥過程自由能的變化，在理論上都可以用水分活度來解析。基于水分活度與溫度和含水率間的關系式（18），便可得到任意溫度區間[273.15,T]上的自由能比的變化規律。

物料水分活度也是無量綱，其變化區間是(0,1]。從圖4b看出，在同一水分活度下，不同溫度條件下的含水率差的變化規律是沿0到最大，然后再趨向于0的過程。同樣，在同一含水率條件下，不同溫度條件下的水分活度差的變化規律也是沿由0到最大，然后再趨向于0的過程。小麥含水率在 30%以上時，水分的活度非常接近自由態，而在含水率低于5%以后，水分活度很小，且隨含水率的降低非常緩慢，表明物料對水分的牽制力隨含水率降低而迅速增大，且是非線性過程。

圖4c是不同溫度條件下，小麥水分汽化時的自由能比隨含水率變化。由圖4c看出，在任何溫度條件下，小麥水分汽化時的自由能比隨物料含水率的降低而增大，而在相同的含水率條件下，溫度越高，自由能比越小，表明提高溫度，相應地增大了干燥動力，相對降低了物料水分汽化時的自由能消耗。

干燥速率比是無量綱，對于 2個幾何相似的干燥工藝系統，在物料水分活度或者物料水分活度與介質相對濕度差相同的條件下，則對應干燥速率與其同等條件下的最大干燥速率之比必然相等。干燥速率比越小，表明物料與水分間的結合能越大，這是物料自身固有的內在屬性。由于式（15）對應的是介質相對濕度等于 0時的情況，所以，它揭示的是物料自身固有的理論過程，是表征一切物料的干燥過程的一般關系式。無論水以何種形式存在于物料中，也無論干燥的一切機理參數如何變化，干燥現象都可以由其干燥速率比狀態函數來表達。圖4d是解析的不同溫度條件下，小麥的干燥速率比隨含水率變化規律。從圖4d看出，在同一理論干燥速率比下，不同溫度條件下，含水率差的變化是沿由 0到最大，然后再趨向于 0的過程，同樣，在同一含水率條件下，不同溫度條件下的水分活度差變化也是由 0到最大，然后再趨向于0的過程。含水率在25%以上時，理論干燥速率比的變化很小，而在 25%以下時，干燥速率比較快地降低，在相同的含水率條件下，溫度越高，干燥速率比相對越高，但當含水率降至約5%以后，溫度對干燥速率比的影響明顯減小。圖4d中各曲線間的縱坐標差和橫坐標差的變化，清晰地呈現了小麥的干燥過程同時受溫度和含水率的影響這一客觀事實。解析結果，為實現高效節能干燥，依據物料的干燥狀態，合理地匹配干燥條件參數，提供了理論依據和解析的新方法。

比較圖4中a、b、c和d圖中的曲線，不難發現，小麥在含水率在 25%以上時，溫度和含水率的變化對比自由能消耗，自由能比，水分活度和干燥速率比的影響都很小，表明當物料處于高含水率狀態時，水分活度接近于1，自身擁有較大的去水動力，提高溫度對干燥過程的影響并不顯著。隨著含水率降低（如圖4d中的25%～10%含水率段），溫度和含水率的變化對比自由能，自由能比，水分活度和干燥速率比的影響較大，且均為非線性變化，此時，提高干燥溫度，能夠明顯地增大自由能、水分活度和干燥速率比，降低自由能比，強化干燥過程。

3 干燥特征函數及其理論解

3.1 蒸發過程中的技術功

在實際干燥過程中，物料內部存在的含水率偏差，不同位置上的水分活度不一定相等，對應水分活度，所呈現的水蒸汽分壓力也不一樣，在汽化面內的壓力狀態變化是由，由汽化面到邊界面混合區間的壓力變化是由。

由圖 2知，物料水分汽化經歷汽化和與汽化面上方水蒸汽混合兩個連續變化的過程。當介質中的水蒸汽分壓力不為0時，水分蒸發不僅要克服結合能做功，同時，還受外部介質中的水蒸汽分壓力的影響，而使汽化的水分量減少，此時，蒸發份數，由汽化面運動到邊界面的實際壓力變化范圍是[ps-pe,p-pe]。在此用F(μ)表示，汽化份數克服結合能做功消耗的自由能原函數，服從式（7），基于壓力函數與其原函數（自由能）間的關系，其消耗的份額則服從C1是積分常數。當pe=0 時于是得到

水分汽化后與汽化面上方的水蒸汽混合，其壓力變化同樣是連續過程。就物料水分汽化微元體上壓力而言，汽化所呈現的壓力是初態壓力pc，而汽化面上方的水蒸汽壓力是p，當外部介質的水蒸汽分壓力為pe時，蒸發份數則隨pe的增大而減少，所以，蒸發份數呈現的壓力變化范圍是[pc-pe,p-pe]。在此，用符號F(p)表示混合過程中，壓力函數的原函數（自由能），那么，該過程所消耗的自由能份額則服從F(p) = -vdp+C，C是混合22區間的積分常數。當pe=0時，F(p)=0，于是得到

在此用符號μx表示蒸發份數相對于自由態蒸發 1kg水時的自由能減少量，并稱μx為同比自由能消耗，單位是 kJ/kg。那么，μx則是F(μ)與F(p)兩項之和，即μx=F(μ) +F(p)，于是，得到積分式（19），求解得到μx的解析式（20）。

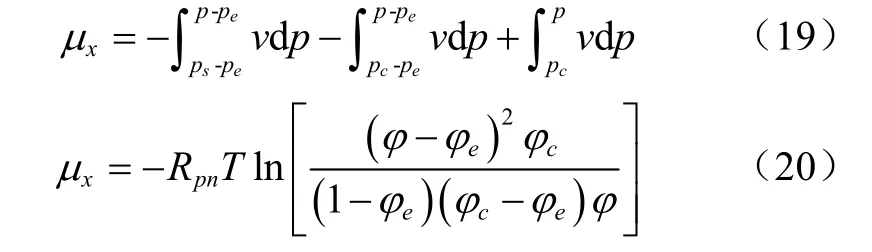
自由能消耗，是自發過程物系減少內能轉化為技術功的度量，式（20）表征的是水分從物料中蒸發時與在自由態下汽化1 kg水相比，多消耗的自由能。由式（14）知，消耗的自由能增加，等同于蒸發的水分量減小，呈現干燥速率降低。基于的式（14）和式（15），得到對應不同介質條件的干燥速率比表達式（21）和式（22）

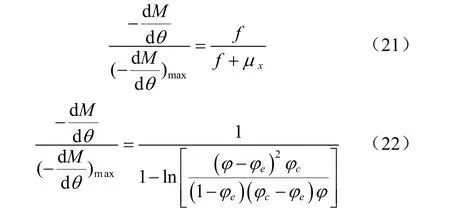
式中φe是干燥介質的相對濕度（小數），φ是對應物料含水率為M時的水分活度（小數），φc是物料的初始水分活度（小數）。

式（22）是狀態函數，其值取決于物料的初始水分活度、水分活度和干燥介質相對濕度（物料平衡水分活度）；它是基于水分活度表達的的一般性關系式，反映的是一切物系中，物料和介質交互作用的情況。由于干燥是水分單一組分汽化、遷移的物系，而水在相平衡條件下的汽化壓力是飽和蒸汽壓，所以，這個壓力就是汽化面內蒸汽壓，它是溫度的單值函數。汽化后（蒸發份數），在與蒸發面上方的水蒸汽混合過程中的壓力變化經歷的是由對應初態水分活度時的壓力pc趨向于給定的外部介質中的水蒸汽分壓力（平衡壓力）的狀態變化過程。

因為物料內部含水率偏差消失的速率很緩慢，與水蒸汽壓力波傳播的速率相比，可以忽略不計。物料在相平衡條件下，其水分活度在數值上等于介質的相對濕度，即，由此可見，在同一溫度條件下，水蒸汽分壓力與水分活度一一對應，基于相平衡條件下試驗得到的物料水分活度，能夠客觀真實地反映其對應的水蒸汽壓力，那么，基于物料內部不同位置上的壓力變化，則可客觀地反映出所處位置的水分活度變化，這樣一來，按照圖 2所示的蒸發過程中，不同位置上的壓力值及其在汽化、混合過程的狀態變化，就可以解析出內部的水分活度分布及其含水率偏差。

3.2 干燥速率特征函數的理論解

3.2.1 最大汽化速率常數

不同的物料在不同的干燥工藝和介質條件下的干燥特性不同，但對于特定的物料，在特定的干燥工藝和介質條件下，對應其干燥區段，均存在相應的干燥速率最大值，且發生在物料內部水分均勻一致（物料內部無水分偏差）的情況下，把此時且水分活度等于 1時的干燥速率稱為最大汽化速率，并用符號C0表示，kg/h。基于式（22），得到C0的計算式（23）。

3.2.2 干燥機理函數的理論解

物料在干燥過程中所能去除的水分稱為自由水，在平衡狀態下所含的水分稱為平衡水。在此，用符號M0、M和Me分別表示物料的最大極限含水率、含水率和平衡含水率，自由含水比則被表示為(M?Me)/(M0?Me)。基于濃度擴散，干燥速率則正比于含水率差，即(M?Me)，在此用k表示干燥常數，h-1，按照菲克定律，在[M0，Me]含水率區間內，干燥速率和最大汽化速率可表達為式（24）和式（25）[6]。

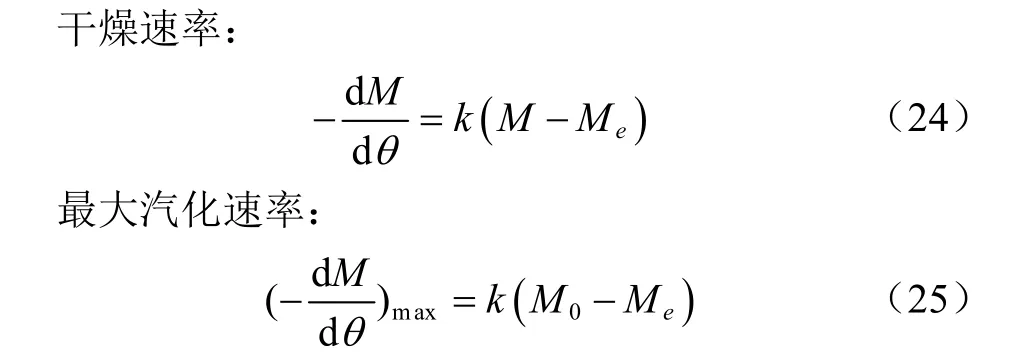
式中M是物料的干基含水率，%，M0和Me分別是極限含水率（水分活度等于1）和平衡含水率，%，k是干燥常數，h-1。

用式（24）除以式（25）得到自由含水比與干燥速率比關系式（26）

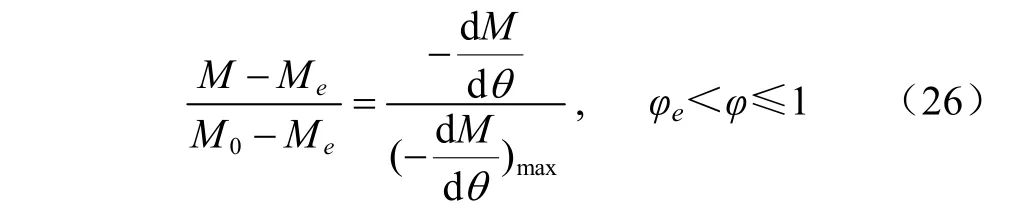
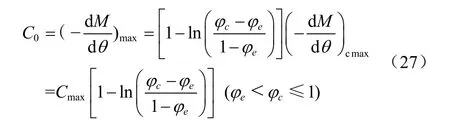
由式（23）、式（26）和式（27）得到對應物料在實際含水率區間M[Mc,Me)上的自由含水比變化的理論表達式（28）

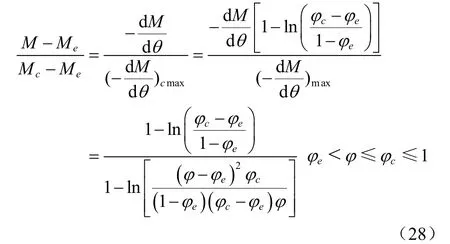
式（28），表征物料干燥的機理，在此用f(φ)表示的變化規律，于是，得到干燥機理函數的數學表達式（29）。

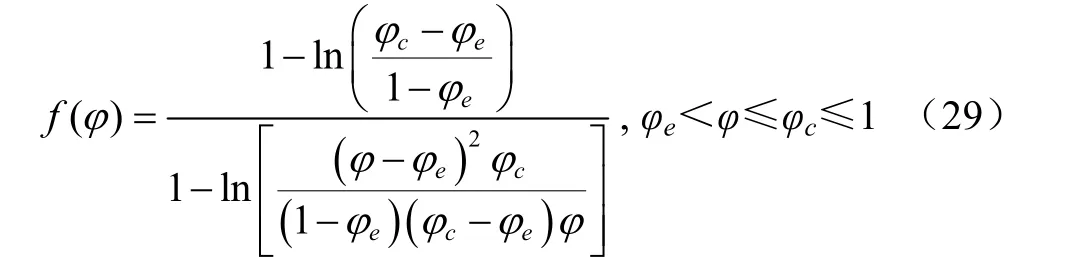
3.2.3 干燥速率的理論解

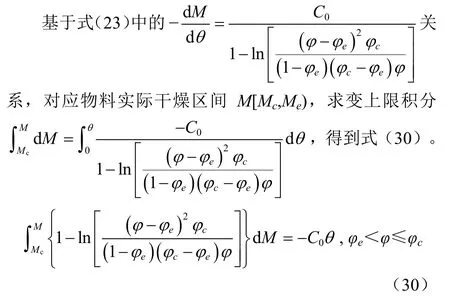
用式（28）中的含水率對物系的水分活度求微分得到關系式（31）

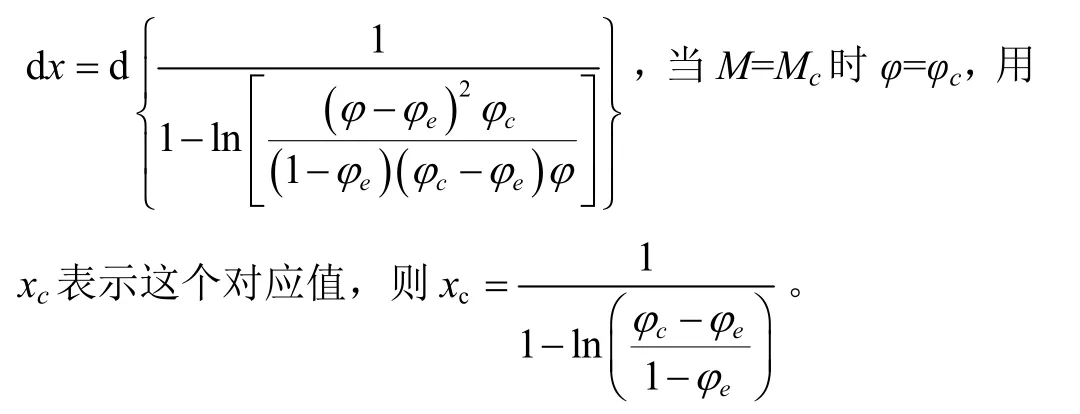
把式（31）中的dM代入式（30）并變換積分上下限,得到水分活度隨時間變化的積分通式（32）。

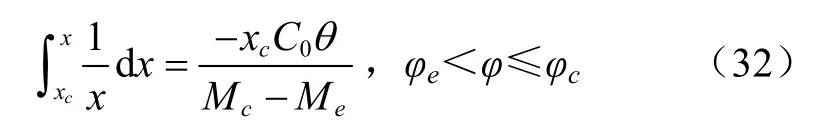
求解式（32）并把x、xc和式（27）代入后得到物系水分活度與時間的關系式（33）

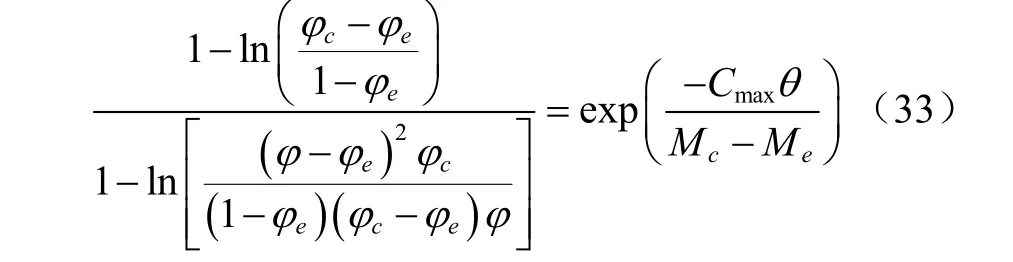
式（33）建立了物料水分活度，初態的含水率，初態水分活度，平衡含水率，平衡水分活度和區間最大干燥速率之間的內在關系。

把式（33）代入式（28），得到基于M[Mc,Me)實際干燥區間的自由含水比理論表達式（34）。

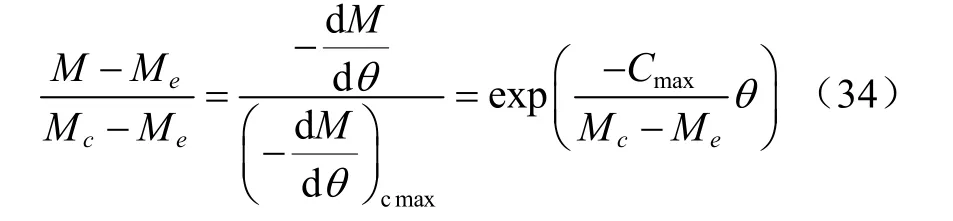
在式（34）中Cmax是實際過程中，M[Mc,Me]區間的干燥速率最大值。式（34）表明在穩態介質條件下，任意物料干燥過程均服從指數模型，在區間[Mc,Me]上，干燥常數的理論解是

由式（34）得到M[Mc,Me]區間的干燥速率表達式（35）

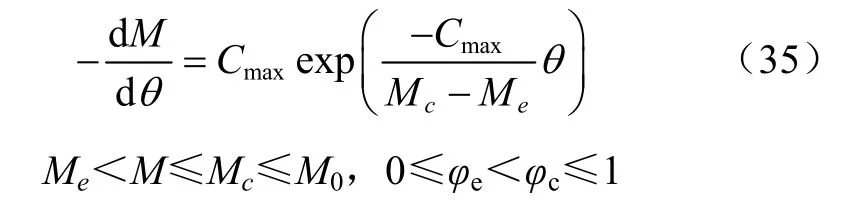
由式（35）看出干燥速率隨時間的變化也服從指數模型，其值取決于物料的初始水分活度、平衡含水率、區間最大干燥速率和初始含水率。在物料初始水分活度等于1時，Mc=M0、φc=1，此時，指前因子等于最大汽化速率。

3.3 討 論

水分擴散，依賴濃度的現象普遍存在，已有諸多關于此方面的通論，氣態物質自發遷移的動力是壓力的單值函數，是不爭的事實，所以，是否存在擴散現象，則取決于是否存在壓差。為從理論上對實際過程定量描述、研究人員在等溫條件下測量 2種物系的熱量比，表征汽化潛熱系數比[43]，基于這個比，成功地建立了過程量與狀態量之間存在內在聯系，但存在的問題是，要得到客觀真實的試驗測定值非常困難，根源在于熵是抽象的熱力學函數，在自發過程中一定存在熵增且在不同過程間的可比性很差，往往導致測量結果偏離實際。

由于一切過程中物系間的相互作用，本質上都是體現在能量的傳遞和轉換，在一切自發過程中，自由焓的變化量，始終服從 dh=cpdT。自由焓的減少量，在數值上就是汽化份數克服物系阻力所輸出做的功，所以，以自由能為統一尺度，可以，完整地從理論上解析出實際過程。

對于溫度為T，壓力為P，體積為V，摩爾量為n的理想氣體混合物，服從狀態方程PV=nRT。基于道爾頓分壓力定律，得到該物系中，各種組分的分壓力與總壓力之比和其摩爾數與總摩爾數之比，即壓力比和摩爾成分或者體積成分間的關系式

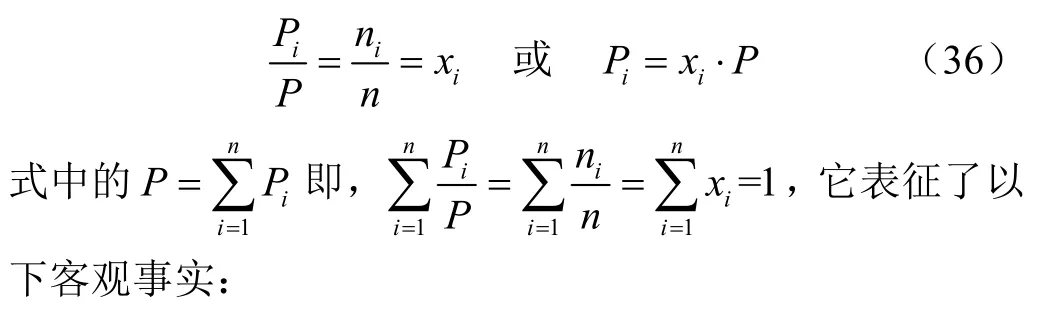
1）道爾頓分壓力定律表明了理想氣體混合物的總壓力等于各組成氣體的分壓力之和。

2）壓力比與氣體常數無關，在數值上等于質量成分和體積成分。

3）各組成員的分壓力與總壓力比（簡稱壓力比）等于體積成分，它與總體積無關。這是因為在同溫度同壓力條件下同摩爾數的任何理想氣體占居的體積都相等，而在任何條件下

4）各組成元的分壓力與總壓力比（簡稱壓力比）與溫度，總體積，總壓力，總摩爾數無關，在數值上等于質量比。這是因為摩爾數的值的完全取決于質量，質量成分與溫度等其他一切過程因素無關，壓力比也是與溫度、體積等其他一切過程因素無關的物理量。

由此可見，壓力比雖然是基于理想氣體建立的，但它具有普遍意義，適合于一般氣體質量混合的一切實際過程。

干燥是濕物料與外部介質，通過邊界進行能量和質量傳遞與轉換的開口系統。水分汽化，運動受物料和外部介質的雙重作用，完全體現在水與絕干物質組分間的結合能和運動的阻力。二者綜合作用的結果則完全反映在物料的干燥速率，干燥速率的變化，完全取決于物系中的水蒸汽分壓力的狀態。而在外部的水蒸汽分壓力恒定不變條件下，系統內部的水蒸汽分壓力則經歷無數中間狀態，由初始的的準平衡過程。

當pe=0時，不存在外部水蒸汽分壓的影響，干燥過程完全取決于物料自身，所以，在pe=0的條件下，便可完整地解析出物料水分的結合能。對應外部條件，基于壓力函數及其原函數（自由能消耗）和相平衡條件下得到的水分活度與其一一對應的壓力關系，能夠肯定數據的客觀性，而按照汽化、混合過程壓力變化的位置和區域，解析物料內部的水含水率分布，基于自由能揭示干燥特征函數并得到理論解，無論在邏輯上還是理論上都成立。

4 結 論

干燥物系的自由含水比和干燥速率是對應外部條件，物料水分活度、溫度和初始含水率及其分布的狀態函數，從理論上揭示了以下事實：

1）無論水以何種形式存在于物料中，也無論干燥的一切機理參數如何變化，干燥現象都可以由其自由能傳遞和轉換來定量表達。

2）基于物料的最大汽化速率C0、初始態水分活度φc、平衡條件下的水分活度φ和介質相對濕度φe，可以從理論上揭示出實際過程干燥速率的變化，其關系是M是含水率，%，θ是干燥時間，h。

3）干燥是物料自身的狀態變化過程，它是以外部約束為條件條件，干燥機理函數的理論表達式是

4）在干燥過程中，物料的自由含水比等于干燥速率比且隨時間的變化服從指數模型，其理論表達式是干燥速率隨時間變化服從最大汽化速率的理論解其中，Mc、Me和Cmax分別是初始含水率、平衡含水率和區間干燥速率特征常數。