基于Fluent的鋰離子電池及模組風冷溫度場數值研究

劉顯茜 鄒濤 侯宏英 徐梽宇 王星博

摘 要：為了研究鋰離子電池充（放）電過程中熱性能特點，更好地進行熱管理分析，基于Fluent軟件建立鋰離子電池組三維瞬態散熱模型并對溫度場進行仿真計算，分析不同條件對電池及模組散熱性能的影響。結果表明：減小充（放）電倍率和增大表面對流換熱系數可改善電池因溫度過高而導致的熱失控。進口風速從0.5 m/s增至6 m/s且4C充電終止時，電池組最高溫度、平均溫度、溫差、一致性系數降低了33.57 K、21.23 K、9.84 K和2.82%，但泵功耗增加了0.35 W。進風溫度從298.15 K降至283.15 K且4C充電終止時，電池組最高、平均溫度降低12.8 K和13.92 K，溫差與一致性系數升高1.86 K和0.76%。即增大風速，電池組溫升和溫度均勻性得到改善;降低進風溫度，可控制電池組溫升，但溫度均勻性抑制效果變差。

關鍵詞：鋰離子電池;散熱性能;充（放）電倍率;對流換熱系數;進口風速;進風溫度

DOI：10. 11907/rjdk. 192465 開放科學（資源服務）標識碼（OSID）：

中圖分類號：TP301文獻標識碼：A 文章編號：1672-7800（2020）007-0005-06

Numerical Study of Air Cooling Temperature Field of Lithium-ion Battery and Module Based on Fluent

LIU Xian-xi1，ZOU Tao1，HOU Hong-ying2，XU Zhi-yu1，WANG Xing-bo1

（1. Faculty of Mechanical and Electrical Engineering， Kunming University of Science and Technology， Kunming 650500， China;

2. Faculty of Material Science and Engineering， Kunming University of Science and Technology， Kunming 650093， China）

Abstract： In order to study the thermal performance characteristics of lithium-ion battery during charge and discharge for better thermal management analysis， based on Fluent， a three-dimensional transient heat dissipation model of lithium-ion battery was established and the temperature field simulation calculation was carried out to analyze the influence of different conditions on the heat dissipation performance of the battery and module. The results show that reducing the charge or discharge rate and increasing the surface convection heat transfer coefficient can improve the thermal runaway of the battery due to excessive temperature. When the inlet wind speed increased from 0.5 to 6 m/s and the 4C charge was terminated， the maximum temperature， average temperature， temperature difference and consistency coefficient of the battery pack decreased by 33.57， 21.23， 9.84 K and 2.82%， but the pump power consumption increased by 0.35 W. When the inlet air temperature dropped from 298.15 to 283.15 K and the 4C charge was terminated， the maximum and average temperature of the battery pack decreased by 12.8 and 13.92 K， and the temperature difference and the consistency coefficient increased by 1.86 K and 0.76%. That is， the wind speed is increased， and the temperature rise and temperature uniformity of the battery pack are improved. Lowering the inlet air temperature can control the temperature rise of the battery pack， but the temperature uniformity suppression effect is deteriorated.

Key Words： lithium-ion battery; thermal performance; charge and discharge rate; convective heat transfer coefficient; inlet wind speed; inlet air temperature

0 引言

鋰離子電池因能量密度大、高效率、低自放電和循環壽命長等優點被廣泛用作電動汽車的儲能系統[1]，但充放電過程大量熱累積導致電池組溫度升高，易造成電池熱失控而產生安全事故。因此，良好的散熱方式對保證電池組的正常工作、使用壽命、安全性、可靠性至關重要[2]。

電池組散熱方式主要包括空氣、液體、相變材料（Phase Change Material， PCM）和熱管冷卻[3]。液體冷卻對密封性要求高，存在漏液可能;相變冷卻過程中PCM體積變化易引發泄露，在大規模電池組中其熱管理系統應用性較差;熱管冷卻結構復雜、加工工藝和材料成本要求高，因此限制了以上散熱方式的普及[4]。與以上冷卻方式相比，空氣冷卻因制造成本較低、布局簡單、系統可靠性高、質量相對較輕和無漏液等受到廠商青睞[5-6]。歐陽唐文等[7]對鋰單體電池放電狀態下計算穩定生熱速率并進行三維溫度場仿真，但實際充（放）電過程中受電池內阻和電荷狀態（State of Charge， SOC）等因素影響，其生熱速率并非恒定，應加以考慮;趙韓和方雄燦[8]建立電池組風冷三維仿真模型，通過改變箱體角邊形狀降低電池組最高（低）溫度和溫差;Liu等[9]通過周期性逆轉氣流產生的往復空氣流動有效改善電池組局部過熱現象，提高電池組溫度場一致性;Wang等[10]研究強制風冷電池組矩形排列、六邊形排列、圓形排列以及風扇安裝位置對電池組散熱性能影響。但文獻[8-10]多以最高溫度和溫差作為電池組散熱能力指標，其評價體系較單一，缺乏體現電池組溫度分布均勻性指標。因此，本研究引入溫度場一致性系數完善電池組溫度分布均勻性分析。

本文建立單體電池生熱速率模型和電池熱傳遞模型，通過ANSYS Workbench/Fluent在空氣冷卻條件下分析充（放）電倍率和表面對流換熱系數對單體電池溫度場分布的影響。建立鋰離子電池組三維散熱模型，研究進口風速和進風溫度對電池組最高溫度、平均溫度、溫差以及溫度場一致性系數影響，為電池熱管理設計提供參考。

1 物理模型

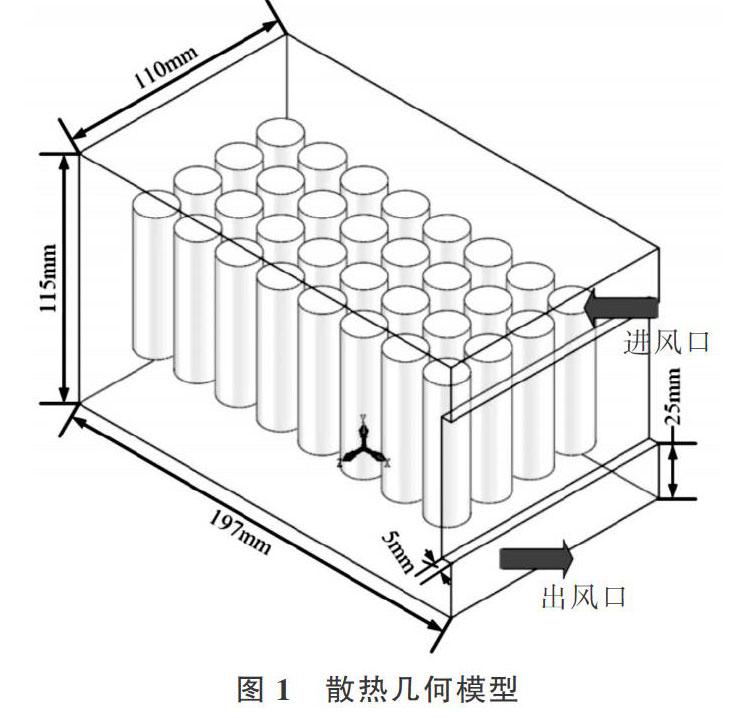
以18650鋰離子電池為研究對象（直徑18.2 mm，高65 mm），其額定容量1 500 mAh，標稱電壓3.7 V，最大（最小）電壓為4.2（3.0）V[11]。采用4×8的順序排列（共32個單體電池），散熱幾何模型如圖1所示。Lu等[12]設計的電池組三維模型計算表明進、出風口同向布置散熱性能優于異向布置，因此研究中選擇進、出風口同向布置。電池箱體進、出風口長寬分別為110 mm和25 mm，各單體電池橫向間距和縱向間距均為4 mm，外圍電池與箱體左右壁面、前后壁面間距分別為13 mm和10 mm，電池與箱體頂（底）間距為25 mm。為簡化計算，忽略電池間連接電路及電池底座對電池組散熱的影響。散熱模型沿Z軸方向對稱，為提高計算速度和減少計算成本，取其1/2為研究對象。

2 數學模型

2.1 流體控制方程

連續性方程如式（1）所示。

動量方程如式（2）—式（4）所示。

能量方程如式（5）所示。

其中，ρ為空氣密度;U為速度矢量;u、v、w為U在坐標系x、y、z方向的分量;μ為空氣動力粘度;對于粘性系數為常數的不可壓縮流體，Su=Sv=Sw=0;ST為流體內熱源及因粘性作用流體機械能轉換為熱能部分;k為空氣熱導率;Cp為空氣比熱容。

2.2 電池熱傳遞模型

假設電池由各向同性、均勻、不透明材料組成，電池輻射與對流傳熱占比很小，電池內部熱傳遞方式主要為熱傳導，在柱坐標下電池熱傳遞的能量守恒方程如式（6）所示。

其中，ρb為電池平均密度;Cpb為電池比熱容;Tb為電池熱力學溫度;t為時間;λr、λφ、λz分別為柱坐標下r、φ、z 3個方向的熱導率;q為電池單位體積生熱速率。

采用Bernardi[13]提出的鋰離子電池單位體積生熱速率模型，生熱速率q表達式如式（7）所示。

其中，V為電池體積;I為充（放）電流（放電時：I < 0，充電時：I > 0）;U0為電池開路電壓;U1為電池端電壓;dU0/dT為溫度影響系數[14]，取定常數0.5 mV/K;U0-U1=IR;R為電池內阻;散熱模型熱物性參數如表1所示。

2.3 條件與參數確定

使用SolidWorks創建好的幾何模型導入前處理器Gambit進行網格劃分、定義邊界條件和區域類型，將輸出的網格文件導入Fluent分析計算，仿真流程如圖2所示。電池內部通過熱傳導將熱量傳遞至電池表面，冷空氣與電池表面進行對流換熱帶走熱量。單體電池間熱輻射很小，為簡化計算過程，可忽略不計。為提高計算精度，電池箱體內氣體域為非結構化四面體網格，固體域為結構化六面體網格。進風口為速度入口，出風口為自由出口，箱體內空氣與電池箱體為無滑移的邊界條件，即在近璧處空氣速度為零。采用基于壓力耦合方程組的半隱式瞬態求解器（SIMPLE算法），壓力、動量和能量方程選擇標準二階迎風格式。電池初始溫度為298.15 K，根據牛頓冷卻定律，電池熱模型邊界條件描述如式（8）所示[16]。

式中，n為電池換熱表面的外法線;h為表面對流換熱系數;Tf為周圍空氣溫度。

定義Tv是衡量電池組溫度場一致性的重要指標[17]，其表達式如式（9）所示。

式中，Tmax、Tmin、Tavg和[ΔT]分別為電池組最高、最低、平均溫度及溫差。溫度場一致性系數（Tv >0），且Tv越接近0表明電池組溫度分布越均勻，一致性越好。

功率消耗P是設計風冷電池熱管理系統的重要參數，可估算為如式（10）所示[18]。

式中，[Δp]為進口與出口間壓降;Q為空氣體積流量。

為便于電池內阻曲線合成，忽略溫度對電池內阻影響，電池內阻與SOC間變化關系可擬合為如式（11）所示[19]。

根據Cheng等[20]提出的SOC估算方法，恒流充（放）電時SOC值與電流和時間成線性關系，計算如式（12）所示。

式中，SOCnew為下一時刻電池SOC值;SOCold為起始時刻電池SOC值;t為電池充（放）電時間，CR為電池額定容量。

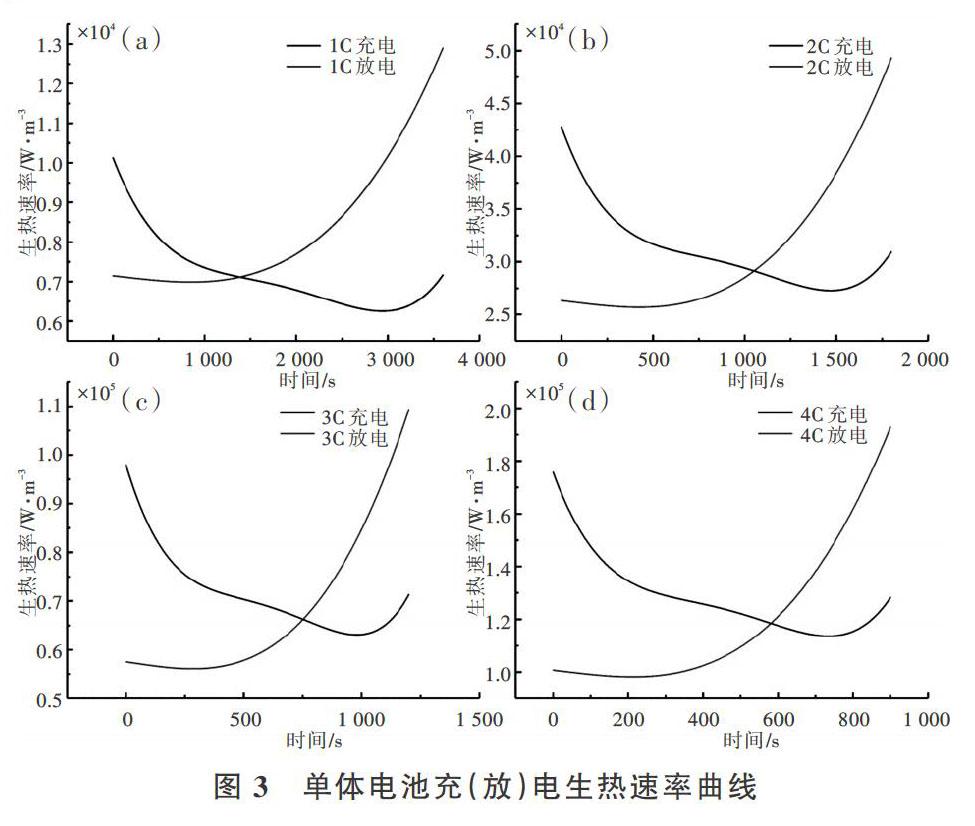
由式（7）、式（11）和式（12）可知，1C～4C充（放）電倍率下單體電池單位體積生熱速率如圖3（a）—圖3（d）所示。充電時，生熱速率先隨時間減小，充電末期逐漸增大;放電時，生熱速率隨時間逐漸增大且斜率也隨之增大，電池生熱量急劇升高。生熱速率隨充（放）電倍率增大呈升高趨勢。

3 單體電池溫度場分析

3.1 充（放）電倍率對電池溫度場影響

在不同充（放）電倍率下電池生熱速率和生熱量相差較大，因此對電池溫度場分布影響顯著。對單體電池在1C、2C、3C和4C倍率進行3 600s、1 800s、1 200s和900s充（放）電瞬態仿真計算。根據文獻[15]研究可知，電池頂（底）面是裸露金屬電極，取對流換熱系數為10 W·m-2·K-1，電池側表面對流換熱系數為5W·m-2·K-1。計算結果如圖4所示，充電狀態，電池平均溫度隨時間升高且斜率逐漸減小，充電開始至終止，電池平均溫度在1C～4C倍率下分別升高4.24 K、13.43 K、23.58 K和34.02 K。放電狀態下，電池平均溫度隨時間升高且斜率逐漸增大，放電開始至終止，電池平均溫度在1C～4C倍率下分別升高5.57 K、14.33 K、23.65 K和33.19 K。同充（放）電倍率（1C、2C和3C）時，前期充電平均溫度高于放電，后期與之相反;4C整充電過程中平均溫度均高于放電，即增大充（放）電倍率，電池溫度上升顯著，為保護其安全使用性能，在滿足使用條件下應盡量減小充（放）電倍率或減少高倍率充（放）電時間。

3.2 表面對流換熱系數對電池溫度場的影響

對單體電池在4C倍率下進行900s充（放）電計算，研究表面對流換熱系數為5 W·m-2·K-1、10 W·m-2·K-1、15 W·m-2·K-1、20 W·m-2·K-1、25 W·m-2·K-1和30 W·m-2·K-1時對電池溫度的影響。文獻[17-19]指出，自然風冷、一般強度和高強度強制風冷的對流換熱系數典型值分別為5 W·m-2·K-1、10 W·m-2·K-1和25 W·m-2·K-1～100 W·m-2·K-1。圖5（a）和圖5（b）為充電和放電狀態下，不同表面對流換熱系數對電池平均溫度隨時間影響。由圖5（a）可知，電池平均溫度隨時間逐漸升高且增幅有減弱趨勢。充電開始至終止，電池平均溫度在對流換熱系數為5～30 W·m-2·K-1時分別上升34.02 K、28.52 K、24.23 K、20.85 K、18.16 K和15.99 K。對流換熱系數從5 W·m-2·K-1增至30 W·m-2·K-1過程中，電池平均溫度逐漸降低，曲線斜率進一步趨緩。隨著充電時間延長，增大對流換熱系數對降低電池平均溫度的效果也較為明顯。同理，由圖5（b）可知，電池平均溫度隨時間逐漸升高且增幅有擴大趨勢，放電開始至終止，電池平均溫度在對流換熱系數為5～30 W·m-2·K-1時分別上升33.19 K、28.71 K、25.14 K、22.27 K、19.93 K和18 K。對流換熱系數從5W·m-2·K-1增至30 W·m-2·K-1過程中，電池平均溫度逐漸降低，曲線斜率也隨之減小。

圖6為充電狀態下對流換熱系數取30 W·m-2·K-1時，電池中心沿軸向和徑向的溫度分布。電池軸向導熱系數遠大于徑向，沿軸向熱傳導速率較徑向快，導致沿徑向溫度變化最大值為0.8 K，而軸向溫度變化最大值僅為0.09 K。

4 鋰離子電池組風冷參數分析

4.1 網格獨立性測試

瞬態仿真過程中，為保證計算結果準確性，對網格進行獨立性測試至關重要[21]。針對圖1散熱模型，選擇? ? ? ?3 056 370、2 365 803、2 291 207和2 220 847共4種網格數量對電池組在4C充（放）電倍率下計算，如圖7所示。充電和放電時，電池組平均溫度最大變化值僅0.12 K和? 0.07 K，滿足測試要求。為節省計算時間、提高效率，選擇2 220 847的網格數用于下列散熱分析。

4.2 進口風速對電池組散熱影響

對電池組在4C充電倍率，環境溫度為298.15 K下，研究進口風速為0.5 m/s、1 m/s、2 m/s、3 m/s、4 m/s、5 m/s和6 m/s時對電池組散熱性能影響。圖8（a）—圖8（d）為不同風速下電池組最高溫度、平均溫度、溫差和溫度場一致性系數隨時間變化。由圖8（a）和（b）可知，電池組最高和平均溫度隨時間升高且增幅逐漸減小。充電開始至終止，電池組最高和平均溫度在風速0.5 m/s～6 m/s時分別上升41.2 K、33.47 K、25.57 K、20.57 K、17.63 K、15.72 K、14.43 K和33.61 K、26.67 K、19.62 K、15.92 K、13.71 K、12.27 K、11.26 K。隨著風速增大，電池與空氣對流換熱增強，電池組最高和平均溫度均降低，且降低趨勢逐漸趨于熱飽和。

由圖8（c）和圖8（d）可知，風速為0.5 m/s和1 m/s時，電池組溫差和一致性系數隨時間升高且增幅逐漸增大;風速為2 m/s和6 m/s時，溫差和一致性系數隨時間升高但增幅逐漸趨緩。充電開始至終止，電池組溫差和一致性系數在風速0.5 m/s～6 m/s時分別上升16.7 K、15.85 K、13.29 K、10.43 K、8.73 K、7.64 K、6.87 K和5.03%、4.88%、4.18%、3.32%、2.8%、2.46%、2.22%。充電前期，較小風速（0.5m/s和1 m/s）時，電池組冷卻性能較差，溫度場較初始狀態變化不大，導致其溫差和一致性系數比2m/s～6m/s時小;充電后期，由圖8（a）和圖8（b）可知，較小風速（0.5 m/s和1 m/s）時的電池組溫升相對較快，而散熱性能緩慢，導致其溫差和一致性系數比2m/s～6m/s時大。

圖9為充電終止時，電池組平均溫度、最高溫度、溫差、溫度場一致性系數、進出口壓降和功率消耗隨風速變化的情形。電池組平均溫度、最高溫度、溫差和一致性系數均隨風速減小并逐漸趨緩，但進出口壓降和功率消耗隨風速增大且逐漸趨陡。該現象歸因于風速增大，進口壓力增量較出口大，結合式（10）便引起圖9現象，即增大風速可有效改善電池組散熱性能，提升溫度場一致性，但過大風速導致這種強化趨勢逐漸減弱且進風口泵功率也隨之增加，偏離節能要求。

4.3 進風溫度對電池組散熱的影響

根據上述研究結果，選擇較為合理風速為4 m/s，在4C充電下，討論進風溫度為298.15 K、293.15 K、288.15K和283.15K時對電池組散熱影響。圖10（a）—圖8（d）為不同進風溫度下電池組最高溫度、平均溫度、溫差和溫度場一致性系數隨時間變化曲線。由圖10（a）和圖（b）可知，298.15 K和293.15 K時，電池組最高和平均溫度隨時間升高且逐漸趨緩;288.15 K時，電池組最高和平均溫度在充電后期出現緩慢下降;283.15 K時，電池組最高溫度在充電后期逐漸下降，平均溫度經過短時溫升后持續降低。充電開始至終止，電池組最高溫度在進風溫度為298.15 K～283.15 K時分別上升17.63 K、13.3 K、9.12 K、4.84 K;平均溫度在進風溫度為298.15 K～288.15 K時分別上升13.71 K、9.05 K、4.42 K，但進風溫度為283.15 K時下降0.21 K。隨著進風溫度降低，電池組最高和平均溫度均有較明顯下降。

由圖10（c）和圖10（d）可知，電池組溫差和一致性系數隨時間升高且增幅逐漸減小（283.15 K充電后期出現小幅下降）。充電開始至終止，電池組溫差和一致性系數在進風溫度為298.15 K～283.15 K時分別上升8.73 K、9.29 K、10 K、10.6 K和2.8%、3.02%、3.3%、3.56%。進風溫度降低，電池組溫差和一致性系數逐漸升高，且在充電后期，改變進風溫度對兩者影響逐漸減小。即降低進風溫度，電池組最高和平均溫度降低，有效防止電池組局部溫度過高而熱失控，溫差和一致性系數升高，出現溫度分布不均現象。

對單體電池和電池組散熱模型進行仿真計算：①增大充（放）電倍率，電池溫度急劇升高，熱失控可能性增加。為考慮其安全適用范圍，在滿足使用條件下應盡量減小充（放）電倍率或減少高倍率充（放）電時間;②增大表面對流換熱系數，電池溫升得到控制，實際運用中可通過增大風速強化對流換熱;③進口風速從0.5 m/s增至6 m/s且4C充電終止時，電池組最高溫度、平均溫度、溫差和一致性系數降低了33.57 K、21.23 K、9.84 K和2.82%，但壓降升高了21.09 Pa，泵功耗隨之增加0.35 W，即增大風速可有效改善電池組散熱性能，但過大風速導致散熱強化趨勢逐漸減弱且進口泵功率也隨之增加，不符合節能設計;進風溫度從298.15 K降至283.15 K且4C充電終止時，電池組最高和平均溫度降低12.8 K和13.92 K，溫差及一致性系數升高1.86 K和0.76%，即降低進風溫度可防止電池組因局部溫度過高而導致的熱失控，但溫度均勻性也隨之變差。

5 結語

運用Fluent流體分析軟件對單體電池和模組進行三維瞬態散熱計算，研究發現可通過減小充（放）電倍率或減少高倍率充（放）電時間以及增大進口風速或電池表面對流換熱系數提升電池組散熱性能，改善電池組溫度均勻性。降低進風溫度可防止電池組因局部溫度過高而導致的熱失控，但無法有效抑制溫度均勻性。由于本文研究均在室溫298.15 K下模擬計算，下一步研究可考慮極端環境下電池組熱性能特點，為電池熱安全設計提供參考。

參考文獻：

[1] FAN Y， BAO Y， LING C， et al. Experimental study on the thermal management performance of air cooling for high energy density cylindrical lithium-ion batteries[J]. Applied Thermal Engineering， 2019， 155： 96-109.

[2] PESARAN A A. Battery thermal models for hybrid vehicle simulations[J]. Journal of Power Sources， 2002， 110（2）： 377-382.

[3] PENG X， MA C， GARG A， et al. Thermal performance investigation of an air-cooled lithium-ion battery pack considering the inconsistency of battery cells[J]. Applied Thermal Engineering，2019，153： 596-603.

[4] 謝金紅. 電動汽車鋰離子電池組散熱結構優化研究[D].? 廣州： 華南理工大學， 2018.

[5] LU Z， MENG X Z，WEI L C， et al. Thermal management of densely-packed EV battery with forced air cooling strategies[J].? Energy Procedia， 2016（88）： 682-688.

[6] 付正陽，林成濤，陳全世.? 電動汽車電池組熱管理系統的關鍵技術[J].? 公路交通科技， 2005， 22（3）： 119-123.

[7] 歐陽唐文，張興娟，楊春信. 基于CFD的鋰電池溫度場仿真[J].? 電子機械工程， 2013， 29（2）： 14-17.

[8] 趙韓，方雄燦. 電動汽車鋰離子動力電池組溫度場仿真及散熱結構優化[J]. 合肥工業大學學報（自然科學版）， 2018， 41（3）： 289-293.

[9] LIU Y P， OUYANG C Z， JIANG Q B， et al. Design and parametric optimization of thermal management of lithium-ion battery module with reciprocating air-flow[J].? Journal of Central South University， 2015， 22（10）： 3970-3976.

[10] WANG T， TSENG K J， ZHAO J， et al. Thermal investigation of lithium-ion battery module with different cell arrangement structures and forced air-cooling strategies[J]. Applied Energy， 2014， 134： 229-238.

[11] SABBAH R，KIZILEL R， SELMAN J R，et al. Active （air-cooled） vs. passive （phase change material） thermal management of high power lithium-ion packs： limitation of temperature rise and uniformity of temperature distribution[J].? Journal of Power Sources， 2008， 182（2）： 630-638.

[12] LU Z， YU X，WEI L，et al. Parametric study of forced air cooling strategy for lithium-ion battery pack with staggered arrangement[J].? Applied Thermal Engineering， 2018， 136： 28-40.

[13] BERNARDI D，PAWLIKOWSKI E，NEWMAN J.A general energy balance for battery systems[J].? Journal of the Electrochemical Society， 1985， 132（1）： 5-12.

[14] 趙衛兵. 電動車鋰電池熱管理系統研究[D]. 長春：吉林大學， 2014.

[15] 郭立剛. 鋰離子動力電池熱分析及散熱優化[D]. 西安：長安大學，2016.

[16] 楊世銘，陶文銓.? 傳熱學[M]. 北京：高等教育出版社， 2006.

[17] 程昀，李劼，賈明，等. 動力鋰離子電池模塊散熱結構仿真研究[J]. 中國有色金屬學報， 2015， 25（6）： 1607-1616.

[18] JILTE R D， KUMAR R， MA L. Thermal performance of a novel confined flow Li-ion battery module[J].? Applied Thermal Engineering， 2019， 146： 1-11.

[19] 彭強. 電動汽車用鋰離子動力電池熱效應研究[D]. 長春：吉林大學，2012.

[20] CHENG K W E，DIVAKAR B P，WU H， et al. Battery-management system （BMS） and SOC development for electrical vehicles[J]. IEEE Transactions on Vehicular Technology， 2011， 60（1）： 76-88.

[21] JIAQIANG E， YUE M， CHEN J W， et al. Effects of the different air cooling strategies on cooling performance of a lithium-ion battery module with baffle[J].? Applied Thermal Engineering，2018，144： 231-241.

（責任編輯：孫 娟）