基于分段序列離散度的異步航跡關聯算法

衣曉，杜金鵬

海軍航空大學，煙臺 264001

在分布式多傳感器多目標跟蹤系統[1-2]中，航跡關聯(即判斷航跡“同源”)是進行信息融合的基礎。然而傳感器開機時機或采樣周期的不同往往導致航跡是異步不等速率[3-4]的，這增大了航跡關聯的難度。

為解決此問題，文獻[5]提出一種基于最小二乘法的關聯算法；文獻[6]利用順序成對關聯思想，將關聯問題轉化為廣義似然比檢驗；文獻[7]借助變異蟻群算法解決了最小二乘多維分配問題。文獻[8]組合距離分布直方圖特征，引入機器學習進行特征提取，對航跡插值處理進行時間對齊；文獻[9]利用濾波插值補償全局估計，構造反饋序列，進行自適應航跡關聯。文獻[10]利用插值重構，將測量值與濾波值統一，用偽測量校準時間后再使用經典分配法進行關聯。通過衡量航跡集合之間的最優次模式分配(OSPA)距離[11]，文獻[12]提出一種基于滑窗OSPA距離的航跡關聯算法，但對于不等速率采樣情況下的異步航跡關聯仍需作同步處理。

無論是最小二乘擬合還是拉格朗日插值，異步不等速率航跡關聯問題的傳統解決思路是先通過時域配準[13]將航跡時刻統一，再利用內插外推的方法得到等長航跡序列進行關聯。但時域配準會增加算法運算量，且在同步化過程中，估計值的誤差會發生傳播，這種傳播與濾波誤差有一定相關性，難以進行描述和衡量，從而影響關聯性能。

文獻[14]引入灰理論[15]，用區間灰數表征異步特性，提出了航跡灰關聯算法；文獻[16]通過區實混合序列變換，將航跡序列灰化，利用灰色系統分析進行關聯；文獻[17]使用動態時間規劃，從整體上考慮航跡形狀的相似性進行關聯。文獻[18]則將不同航跡公共測量時間區間劃分為時間窗，計算時間窗權重，應用D-S證據理論或Bayes理論進行關聯。

文獻[16-18]無需時域配準對異步航跡進行關聯，但算法均是以航跡間距離為依據，根據航跡整體形狀相似性或相對位置進行關聯。在實際的航跡交叉、分叉和合并[12,19]現象中，航跡交叉點或航跡分叉合并前后的平行階段，依靠局部航跡間的距離進行航跡關聯往往會導致錯誤關聯。

為避免以局部航跡距離為判據帶來的錯誤關聯，本文將航跡序列作為數據集進行處理，利用分段混合航跡序列的離散度來判斷2條航跡的接近程度。該方法無需時域配準，未引入新誤差，可直接對異步不等速率航跡進行關聯，并且航跡序列的分段處理可有效解決航跡交叉、分叉和合并問題。

1 數據集的離散度度量

定義1混合數據集的離散度

對任意2個數值型數據集X={x1,x2,…,xM}和Y={y1,y2,…,yN}，記(X,Y)=X∪Y為混合數據集，稱

(1)

為混合數據集的離散度。

式中：n=INTL[M/N]；INTL[x]表示不大于x的最大整數；m=MmodN，ymodx表示y除以x的余數；∪為集合“并”運算。

對數據集X={x1,x2,…,xp}，有

nX={nx1,nx2,…,nxp}

2 基于分段序列離散度的航跡關聯算法

2.1 問題描述

假設由2部雷達對公共觀測區域內的多個目標進行跟蹤，雷達標號為s、w，所得航跡標號集合為

Us={1,2,…,ms},Uw={1,2,…,mw}

(2)

記

(3)

為

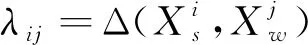
(4)

的估計。

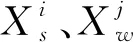
由于離散度表征數據離散程度，航跡交叉現象會對判別產生干擾。如圖1(a)所示，當航跡l2、l3存在交叉現象時，航跡l1與航跡l2、l3的幾何中心w12、w13幾乎重合，由于幾何對稱性，航跡點的離散度基本相同，此時無法判斷航跡l2、l3與l1的關聯情況。但若如圖1(b)所示，將航跡序列分段，則產生的兩段子序列幾何中心不再重合，航跡l1與航跡l2關于幾何中心w12的平均離散度小于航跡l1與航跡l3關于幾何中心w13的平均離散度，可以正確判斷航跡l1與航跡l2關聯。

圖1 交叉和分段處理示意圖Fig.1 Schematic diagram of cross and segmentation

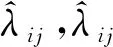
2.2 不等長航跡序列的分段劃分

定義2航跡序列的分段劃分

對航跡序列X={x1,x2,…,xM}進行n段劃分，可得

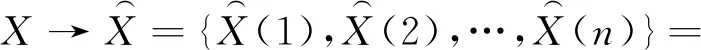
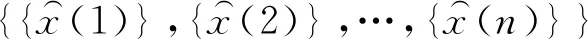
如果滿足：

則稱為航跡序列的分段劃分。

由定義2可知，經過劃分可將航跡序列分為n段子序列。

假設由2部雷達和1個融合中心構成信息融合系統，對公共觀測區域內的多個目標進行跟蹤。設T為融合中心的一個處理周期，在第k個處理周期[(k-1)T,kT]內，雷達s,w上報的航跡數目分別為ms、mw。在第k個處理周期內上報的航跡集合ζs(k)記為

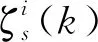
設2部雷達異步，采樣速率不一致但恒定，則在融合中心的同一處理周期內，2部雷達上報航跡的航跡點數目不同，即航跡序列的長度不同，假設來自雷達s的第i條航跡包含ni個航跡點。由于采樣周期不一致，雷達上報航跡的次數亦不同，假設在同一處理周期內雷達s上報a次航跡，來自雷達s第b次上報的航跡集合中第i條航跡記為

在同一處理周期內對多次上報的同批號航跡集合作并集處理，即

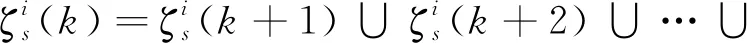
處理后雷達s的第i條航跡記為

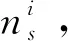
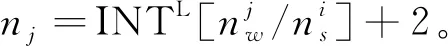
2) 序列分段時，盡可能保證每個分段航跡子序列所含航跡點數目相等。

3) 盡量避免某分段航跡子序列只包含單一航跡點。

4) 原則優先級為：1) ?2) ?3)。

根據以上原則，可保證分段后每組對比子序列航跡點數目之比與原始序列航跡點數目之比基本不變；并確保航跡序列至少分為2段，避免中心交叉問題。

2.3 分段航跡序列離散度的計算

取雷達w的mw條航跡作為比較航跡，雷達s的第i條航跡作為參考航跡。由于每條航跡的航跡點數目不同，根據分段原則，共有mw種分段方式，每種分段方式對應一條比較航跡和參考航跡。

例如在第1個位移分量x上定義分段航跡序列矩陣為Ψx：

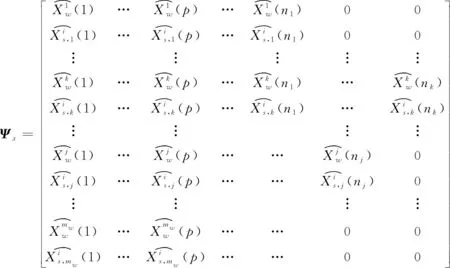
(5)

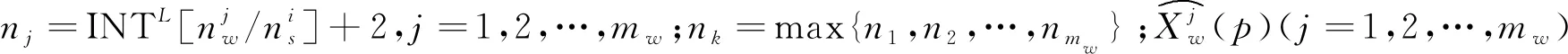
分段航跡序列矩陣Ψx為2mw×nk維，每一行表示每一條航跡在分量x上的分段子序列集合；奇數行元素來源于比較航跡，偶數行元素來源于參考航跡。由于分段數目不同，矩陣各行元素數目不同，故各行缺失元素用0做補齊處理。

根據定義1中對數據集離散度的定義，可計算得到參考航跡和比較航跡的離散度矩陣為

Θx=[δe,f]mw×nk=

(6)

式中：

e=1,2,…,mw;f=1,2,…,nk

(7)

進而可以計算在位移分量x上，來源于雷達s的第i條航跡與來源于雷達w的第j條航跡的離散度，記為

(8)

考慮到位移分量與速度分量具有相關性(導數關系)，并且物理意義的不同導致不同屬性分量間的濾波精度不易比擬，故僅采用位移分量進行關聯。

同理，可以列出在位移分量y上的分段航跡序列矩陣Ψy，相應求解航跡在位移分量y上的離散度，記為λy。對位移分量的航跡離散度進行加權融合，得到在第k個處理周期內參考航跡i(i∈Us)和比較航跡j(j∈Uw)之間的總離散度為

λij=α1λx+α2λy

(9)

式中：加權系數α1、α2為非負實數，且滿足α1+α2=1的約束條件。其數值大小取決于濾波精度，精度越高，權重越大。記狀態濾波協方差矩陣中位移分量x、y的濾波誤差分別為σx、σy，則加權系數為

(10)

2.4 航跡關聯判定

根據所用的指標量離散度λij，可推廣為廣義經典分配法。對于雷達s、w上報的ms、mw條航跡分別計算離散度，構成ms×mw維矩陣，由此將問題轉化為全體航跡的分類問題。

令

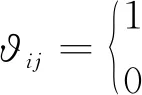
(11)

式中:?ij=1表示航跡i與航跡j關聯；?ij=0表示二者不關聯。目標函數記為

(12)

則形成二維分配問題

(13)

此類二維分配問題，存在匈牙利算法、拍賣算法等經典解決方法，此處不再贅述。分配問題的本質為約束條件下求解目標函數最值的問題，求解算法的不同，求解中多義性的具體表現也不盡相同。

(14)

然后按照2.3節重復計算步驟，直至分配方案呈現唯一性。

分段數目的增加會細化數據處理程度，放大局部航跡的離散度差異，提高度量精度，能有效解決多義性問題。算法的流程如圖2所示。

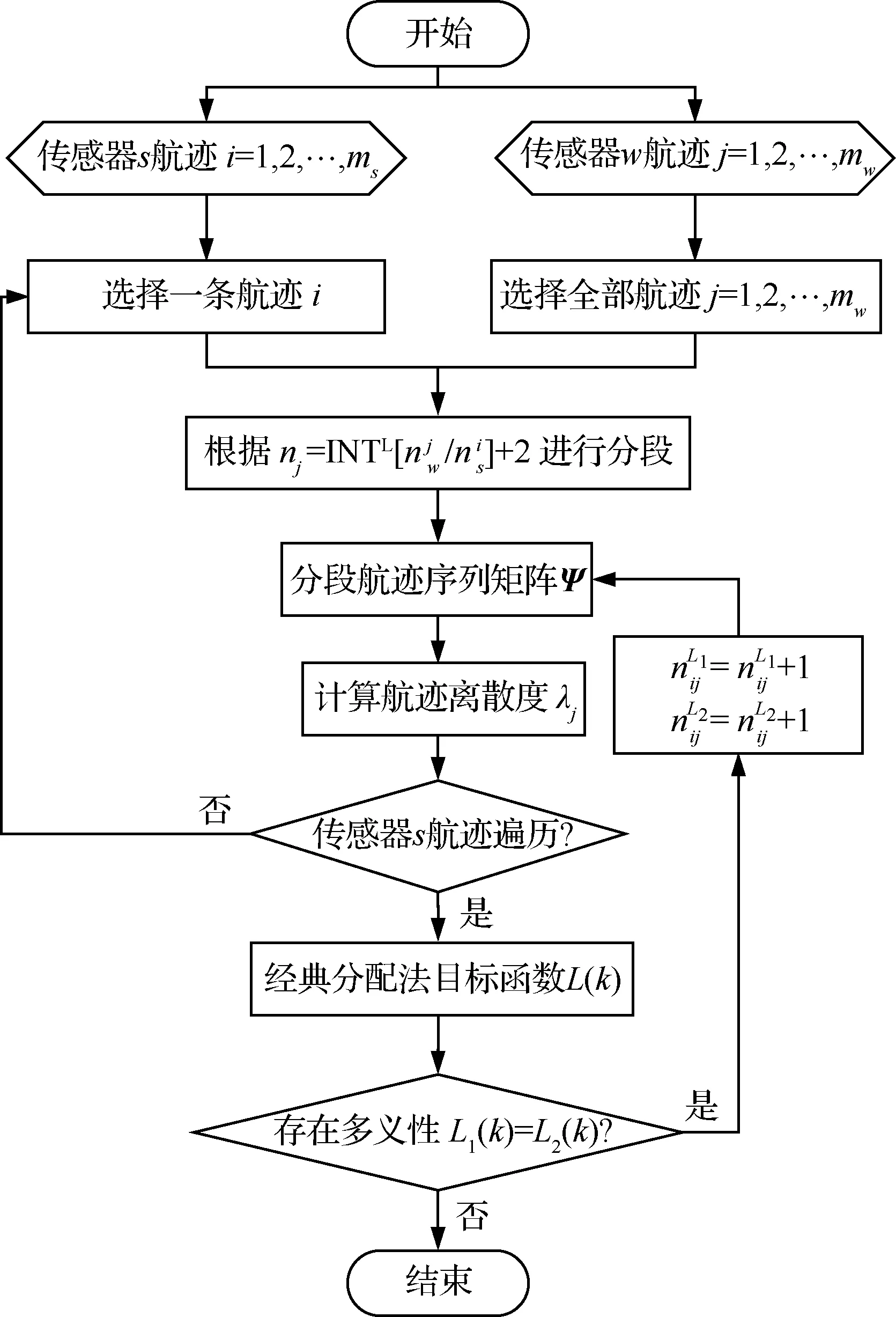
圖2 算法流程圖Fig.2 Flowchart of algorithm

3 仿真驗證與分析

3.1 仿真環境

假設由2部異地配置的2D雷達構成的跟蹤系統對公共區域進行觀測，目標批數為20批，持續觀測時間為30 s。雷達1、2位置坐標分別為(0,0) km, (100,0) km，雷達1的采樣時間間隔為T1=0.2 s，雷達2的采樣時間間隔為T2=0.5 s，并且雷達2比雷達1晚開機0.2 s。

目標運動模型采用二維平面勻速直線運動模型，目標初始方向在0～2π rad內隨機分布，目標初始速度在200～400 m/s內隨機分布。雷達1的測距和測角誤差分別為σr1=150 m、σθ1=0.03 rad；雷達2的測距和測角誤差分別為σr2=180 m、σθ2=0.02 rad。

進行M次Monte Carlo仿真實驗，采用正確關聯率對航跡關聯結果進行評價：

(15)

式中：Ci(k)為第k個處理周期內正確關聯的航跡數目；M為Monte Carlo仿真實驗的次數；N為每次仿真實驗的目標航跡數目。

3.2 算法性能比較與分析

在仿真環境中，進行100次Monte Carlo仿真實驗。在不同條件下對本文算法與文獻[5]中算法和文獻[16]中算法進行比較。

圖3給出了在仿真環境中3種算法關聯結果的比較。可以看出，本文算法的正確關聯率最高，但在采樣初期，本文算法關聯效果較差。這是由于本文算法的離散度屬于統計學度量，采樣初期數據點較少，對關聯的正確性造成了很大影響。

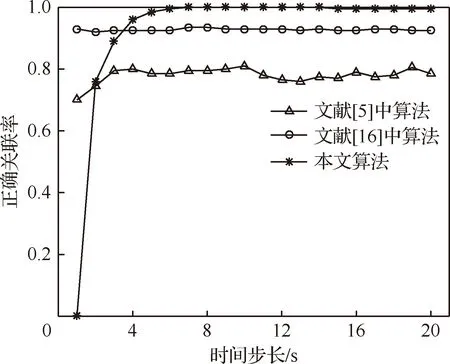
圖3 不同算法的正確關聯率對比Fig.3 Comparison of correct associating rates of different algorithms

但影響持續時間較短，算法可以很快收斂至最佳關聯效果。

在仿真環境的基礎上，改變2部雷達的采樣頻率之比，圖4給出了不同采樣頻率之比對3種算法的影響。本文算法利用同源航跡數據集波動性小的特點進行關聯判定，只關乎航跡點的同源性，航跡點數目(滿足一定統計學數據量)并不會對關聯結果產生影響，故雷達采樣頻率不一致對本文算法無顯著影響。從圖4中可以看出，隨著采樣頻率相差越來越大，文獻[5]中算法的正確關聯率下降較為明顯，而本文算法和文獻[16]中算法的正確關聯率并無明顯變化，與理論結果吻合。

圖4 關聯結果隨采樣率之比的變化Fig.4 Variation of correlation results with changing ratio of sampling rate

在仿真環境的基礎上，根據不同信噪比，改變參數中噪聲的幅值，模擬強雜波干擾。從圖5中可以看出，隨著信噪比的減小，文獻[5]中算法的正確關聯率迅速下降；本文算法和文獻[16]中算法的正確關聯率起初并無明顯變化，在信噪比低于28 dB后有明顯下滑，且文獻[16]中算法的下滑趨勢較快。

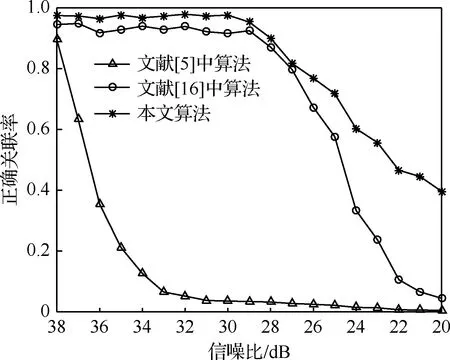
圖5 關聯結果隨信噪比的變化Fig.5 Variation of correlation results with changing SNR

表1給出了不同采樣周期和開機時延下本文算法的平均正確關聯率。可以看出，采樣周期增大，算法正確關聯率有小幅度下降；開機時延并未產生明顯影響。這是由于采樣周期越長，數據量越少，對離散度的刻畫越不準確；而一定范圍內的開機時延只造成數據點在時間上的錯位，并不影響數據分布的離散度。

表2給出了不同噪聲分布形式下本文算法的正確關聯率。可以看出，噪聲的分布形式對本文算法沒有影響。綜合表1和表2可知，本文算法在多種情景下均保持較高的正確關聯率，穩定性較佳。

表1 不同采樣周期和開機時延的正確關聯率

表2 不同噪聲分布的正確關聯率

3.3 航跡分叉合并情況的可辨性分析

在仿真環境的基礎上，調整目標數目、初始位置和初始速度，模擬目標在二維平面上航跡交叉、分叉和合并的情況。當觀測區域中的目標航跡存在大量交叉、分叉和合并現象時，以航跡間距離作為關聯依據的傳統算法，在交叉點或平行階段容易發生錯誤關聯。從圖6可以看出，文獻[5]和文獻[16]中算法的正確關聯率相較于勻速直線模型有所下降；而本文算法由于不依賴距離進行判定，故仍保持較佳的關聯效果。

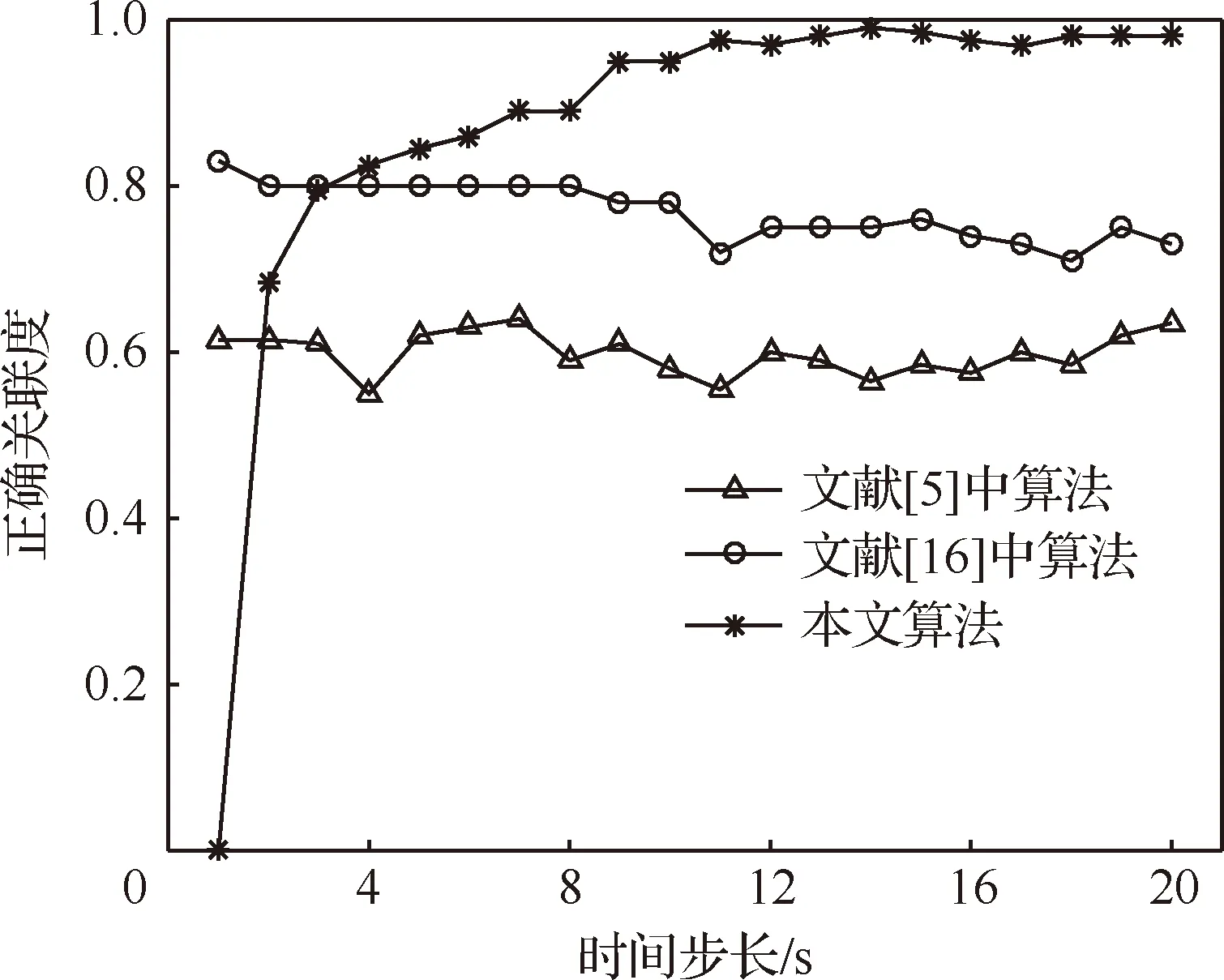
圖6 航跡存在分叉合并時的正確關聯率對比Fig.6 Comparison of correct associating rates of track bifurcation merging

圖7(a)仿真了航跡分叉過程。在開始時刻雷達s、w所觀測2目標進行平行飛行，距離較近，后分別轉向，改為獨立飛行。圖7(b)則仿真了2目標航跡合并過程。開始2目標相距較遠，后組成編隊平行飛行，距離拉近。

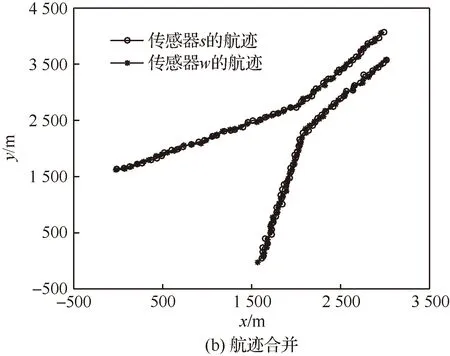
圖7 航跡分叉與合并示意圖Fig.7 Schematic diagram of track bifurcation and merging

圖8仿真了航跡分叉和合并過程中同源航跡{s1,w1}、{s2,w2}和非同源航跡{s1,w2}、{s2,w1}對應的各分段航跡相對離散度的變化趨勢。為直觀反映本文算法對處理目標運動狀態發生突變現象的靈敏程度，細化航跡序列分段為25段予以說明。

圖8 分段航跡序列離散度的變化Fig.8 Variation of segmented track sequence dispersion

從圖8(a)中可以看出，在目標進行平行飛行時，同源航跡和非同源航跡的相對離散度均較小，無法進行有效的航跡關聯。但目標航跡分叉后，同源航跡{s1,w1}、{s2,w2}的相對離散度并未產生變化，而非同源航跡{s1,w2}、{s2,w1}的相對離散度卻迅速增大。

同樣，從圖8(b)中可以看出獨立飛行時非同源航跡{s1,w2}、{s2,w1}的相對離散度較大，同源航跡{s1,w1}、{s2,w2}的離散度較小；但隨著航跡的合并，非同源航跡的相對離散度迅速下降，接近同源航跡的相對離散度。

從航跡交叉合并現象的仿真實驗中可以看出，測度分段航跡離散度的方法可以迅速對航跡狀態突變做出反應，即算法在解決航跡狀態突變問題中具有靈敏度高的特點。即使航跡存在平行飛行階段，只要對各分段航跡的離散度取平均，依舊可以進行準確的航跡關聯。

3.4 算法復雜度分析

圖9給出了3種算法耗時的比較。可以看出，隨著目標航跡數目的增加，3種算法的CPU耗時均呈增加趨勢，但本文算法耗時高于文獻[16]中算法，遠高于文獻[5]中算法。

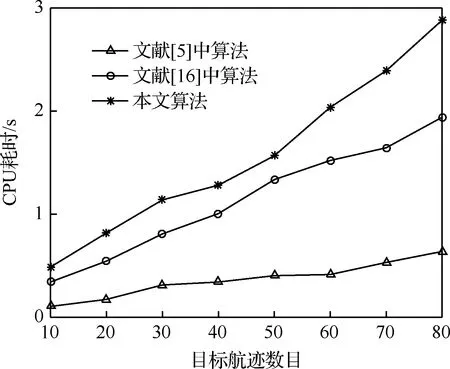
圖9 不同算法的耗時對比Fig.9 Comparison of time consumption of different algorithms

以等長航跡序列關聯為例，假設有m條比較航跡與1條參考航跡進行關聯，各航跡均包含n個航跡點，數據類型為實數類型，計算各算法運算量，如表3所示。顯然，本文算法運算量要高于文獻[16]中算法。

表3 不同算法的運算量Table 3 Calculation amount of different algorithms

4 結 論

1) 本文提出一種基于分段序列離散度的異步航跡關聯算法，給出離散度的具體度量指標和不等長航跡序列的分段劃分規則，并針對多義性問題給出二次檢驗方法。

2) 本文算法無需時域配準，可在多種環境下直接對異步不等速率航跡進行準確關聯，具有穩定性。算法不受噪聲分布的影響，且噪聲強度對算法的影響相對較小，具有良好的抗雜波干擾性。

3) 本文算法可有效分辨航跡交叉、分叉和合并等復雜情況。