線性代數教學方法探索與實踐

李燕娟

摘 要

線性代數是理工科院校必修的一門數學基礎課程，抽象難懂。本文根據課程內容特點，結合教學實踐，對教學方法進行初步探索和實踐，課堂效果良好。

關鍵詞

線性代數;教學方法;矩陣

中圖分類號： G642;O151.2-4 ? ? ? ? ?文獻標識碼： A

DOI：10.19694/j.cnki.issn2095-2457 . 2020 . 18 . 22

線性代數是理工科專業和經管類專業必修的一門數學基礎課，不僅提高學生抽象思維能力、邏輯推理能力，而且為后續專業課的學習奠定一定的數學基礎，使專業課的學習更加得心應手。然而，由于線性代數課程抽象性的特點，學時又少，傳統的教學方法多數以老師為中心的填鴨式、灌輸式等教學模式，很少采用啟發式、案例式等教學方法，教師與學生之間的互動較少，學生被動地接受知識，課堂教學效果不好，且不能充分調動學習的積極性，不利于培養學生學習線性代數的思維能力及探索精神。

如何提高學生學習的積極性、主動性，使學生主觀的參與教學，那么教學方法的選取尤為重要。教學方法的發展是批判繼承繼而改進創新的過程，在線性代數課程的教法設計中，應該注重總結傳統教學方法的實施效果，進而形成與線性代數教學內容相匹配的“靈活性”教法體系[1]。因此，教學方法的選取應該根據學生專業的特點，各個章節內容的特點，靈活的選取不同的教學方法，改進教學現狀，提高課堂教學效果。

1 案例式教學法

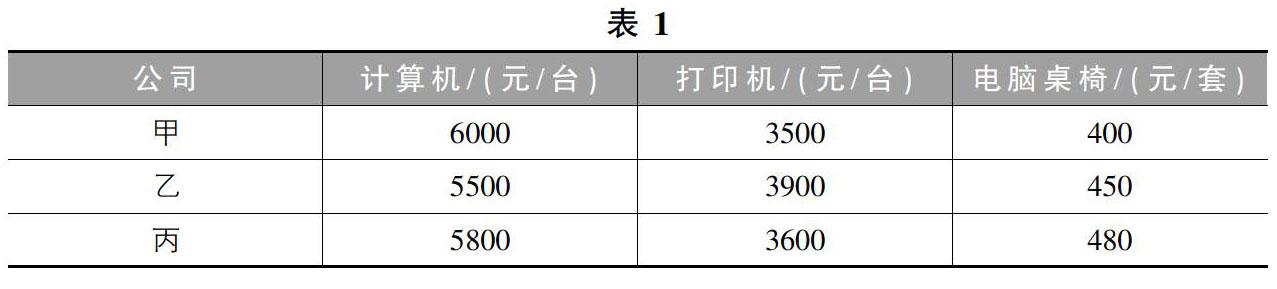
案例式教學法即為在教學過程中引入適當的案例，使所講知識更易簡單明了，知識運用更易通俗易懂。教師可根據學生的專業選取相關的案例，鼓勵學生參與到學習的討論中，激發學生學習的興趣，使學生在輕松的環境中體會所學知識在專業課中的應用，從而提高學習的主觀能動性。比如經管類專業學生在學習矩陣知識時，引入案例：某學校準備組建一個機房，需要指定型號的計算機60臺，打印機10臺，電腦桌椅60套，甲、乙、丙三家公司提供的報價為。

問題：若在一家購買，應選哪家？在講授時，首先分析表格里面的元素不能隨意交換位置，像此類數表就稱為矩陣，引出矩陣的概念，指出是3×3矩陣。在解決問題時，引入可否運用矩陣相乘求得結果呢？設矩陣A=6000 3500 4005500 3900 4505800 3600 480，B=601060，求解AB=419000396000412800，根據結果，易判斷在乙家公司選購，此時，由于計算量較大，可以簡單介紹Matlab中計算矩陣相乘的程序，借助軟件簡化計算量。通過此案例的選取，首先介紹矩陣概念，進而對矩陣相乘的一個實際應用，最后介紹Matlab中關于矩陣的求解，使得學生較易理解概念，學以致用，從而提高學習興趣。

2 啟發式教學法

講數學課不易做到語言生動、引人入勝，但可以思路清晰、語言簡練、不斷提出問題，不斷解決問題從而吸引學生注意力，調動學生積極思考[2]。啟發式教學法能循序漸進，層層深入地講解，使學生帶著問題去聽課，提高注意力。比如在講逆矩陣時，先引入數的運算，當a≠0時，aa-1=a-1a=1，a-1=為a的倒數（或稱a的逆）。提出問題，矩陣是否存在這樣的A-1，使得AA-1=A-1A=E？若存在，可否稱A-1為矩陣A的逆呢？aa-1=a-1a=1成立的充要條件是a≠0，那么方陣A的逆存在的充要條件是否是|A|≠0？在講向量組的線性相關性時，有一個定理是若a1，…，ar線性相關，則a1，…，ar，ar+1，…，am（m>r）線性相關[3]，簡稱為部分相關，則整體相關。提出問題，整體相關，則部分相關嗎？若不一定相關，能否找到一個極大線性無關組呢？進而引出向量組秩的概念。這樣的教學設計，使學生從簡單到復雜，由淺入深的學習過程，比較容易接受新知識，且學習興趣也比較高。

3 對比分析法

對比分析法，就是根據兩個（或兩類）對象間的某些方面，推出它們在其他方面也有相似或相同的屬性[4]，比如第一章行列式和第二章矩陣，兩者的概念完全不同，運用對比分析法，分析兩者之間的不同與相似之處，不同之處在于，行列式符號||，矩陣符號[];行列式是一個數值，矩陣是一個數表;行列式的行數等于列數，矩陣的行數與列數不一定相等。相似之處在于，行列式的性質和矩陣的初等變換有相似之處。通過運用對比分析法，使學生較易接受新概念、新知識，并且分清不同之處，在日后的運用時不易混淆。

在講矩陣的初等變換時，引入例題，解一個非齊次三元線性方程組，先用消元法求解，接著用克拉默法則求解線性方程組，最后用增廣矩陣的初等行變換來解，通過對比分析求解過程，發現用矩陣的初等行變換求解線性方程組更簡單，直觀，學生們也比較容易接受新思想，新方法。

4 總結歸納法

數學教學主要是培養學生的邏輯思維方式，在線性代數的課堂教學中，通過知識點之間的并串聯關系，及時地對其進行總結歸納，只有掌握知識點之間的各種關聯，才能真正理解知識點的概念實質，才能更好地解決問題[5]。如學完第一章行列式，回顧所講內容，先介紹二階、三階行列式，再推廣到n階行列式，再介紹了行列式的性質與運算，在計算方法上介紹了克拉默法則，也可借助知識框架圖，更清晰明了。再比如，第二章講完矩陣之后，要及時歸納矩陣可逆的充要條件。第三章線性方程組講完之后，又可以和第二章緊密聯系起來，以下七個命題等價：（1）方陣A可逆;（2）|A|≠0;（3）A與單位矩陣E等價;（4）A滿秩;（5）A為非奇異矩陣;（6）齊次線性方程組只有零解;（7）向量組線性無關。

向量組線性表示可以與非齊次線性方程組聯系，向量組線性相關性可以與齊次線性方程組聯系。通過歸納總結所學知識，把看似獨立的知識點緊密地聯系起來，使學生心中形成一個知識鏈，有利于日后走向工作崗位養成總結的習慣。

5 抽象具體化法

當講授內容的定義、定理較多時，學生往往覺得知識很抽象，晦澀難懂，這時需要將抽象內容形象化、具體化，可借助舉例說明，在例題中體現定義、定理的思想，使學生能夠找到知識的關鍵點。比如講授行階梯形矩陣，行最簡型矩陣，標準型矩陣時，雖然學生們知道這三類矩陣各自的特點，但問題是怎樣將一個矩陣化為標準型，而有些教材并未涉及相關例題，此時需要舉一些簡單的例子，將先通過初等行變換化為行階梯形矩陣和行最簡型矩陣，再通過初等列變換化為標準型，在化簡過程中要掌握特點。

在介紹完極大線性無關組的定義后，可以舉例α1=10，α2=10，α3=10，求向量組{α1，α2，α3}的一個極大線性無關組。根據定義易得出以下結論：向量組{α1，α2，α3}的極大線性無關組是α1，α2，或者α1，α3，或者α2，α3。通過這個例題的講解，說明兩點內容，一是極大線性無關組是不唯一的，二是極大線性無關組所含向量的個數是唯一的，極大線性無關組所含向量的個數又稱為向量組的秩，使學生能夠明白用定義法怎么確定極大無關組及向量組的秩。

線性代數教學過程是一個動態過程，需根據學生專業、知識水平等情況靈活的選擇教學方法，因材施教。同時，這些教學方法要不斷實踐，在實踐中不斷改進、創新，不但提高自身教學水平，而且有助于提高課堂教學效果，調動學生學習積極性，培養學生的邏輯推理能力，嚴謹的數學思維和創新能力，提高學生在知識經濟時代的適應力。

參考文獻

[1]梁靜靜.線性代數“靈活性”教學方法設計探究[J].科技創新導報，2018（27）：219-220.

[2]王翠香.線性代數課程的特點與教學方法探究[J].大學教育，2019（11）：91-93.

[3]唐曉文，王昆侖，陳翠.線性代數第二版[M].上海：同濟大學出版社，2012.

[4]姜麗穎，張國林.類比方法在線性代數教學中的應用[J].高教學刊，2018（24）：73-75.

[5]孫怡川.淺談獨立學院線性代數課程教學方法的幾點體會[J].科教文匯，2018（12）：51-52.