關于Cramer 法則的再推廣與應用

（喀什大學 數(shù)學與統(tǒng)計學院，新疆 喀什 844000）

設A=（aji）∈Rn×m行滿秩，x=[x1，x2…xm]T∈Rm，b=[b1，b2…bm]T∈Rn，m≥n.給定線性方程組

若令lj=[aj1aj2…ajm]T∈Rm，則線性方程組（2）可改寫為

其中〈·，·〉表示Rm中向量的內積.

通常，利用初等行變換將（2）的增廣矩陣

化為行最簡階梯形后，通過觀察可求得（1）的某些解.特別地，當m=n 且detA≠0 時，（1）的唯一解x=A-1b可由著名的Cramer 公式給出.但是，當m≠n 時，（1）一般不存在用行列式表示的求解公式.基于此，本文將Cramer 法則推廣到求（1）或（2）在R 中的公式解上.

Cramer法則 設A是一階實矩陣.若detA≠0，則線性方程組（1）的解由公式

給出，其中，Ai是用[b1b2…bn]T替換A的第i列后所得到的矩陣[1].

文獻[2]給出了Cramer 法則的一個簡單而有趣的推廣，即

Burgstahler定理 若線性方程組

有唯一解x1，x2，…，xn，則對?λi∈R，有

1 主要結果

定理1對?b∈Rn，線性方程組（1）有解的充分必要條件是

在定理1 有解的情況下，（1）的解由公式

給出，其中A*是A的轉置（在復數(shù)域C 中是的共軛轉置）.

推論 若n=m，則線性方程組（1）、（2）和（3）由公式（9）給出的解可寫成

形式，并且它還是（1）、（2）和（3）的最小范數(shù)解.

證明 注意到，當n=m 時，（9）與Cramer 公式一致.事實上，（9）可以由公式

給出，其中（AA*）j是將AA*的第j 個列向量用b=[b1b2…bm]T替換后所得到的矩陣.同時，（11）還是最小范數(shù)解[3]，即

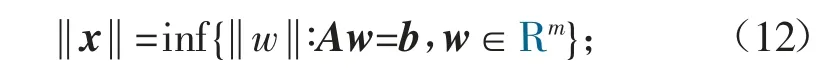
特別地，‖x‖=‖w‖且Aw=b?x=w.

定理2對?b∈Rn，線性方程組（1）有解的充分必要條件是A的行向量組{l1，l2，…，ln}在Rm中線性無關.在有解的情況下，（1）的解由公式

給出，其中向量集（v1，v2，…，vn）（vj=[vj1，vj2，…vjm]T，j=1，2，…，n）可由Gram-Schmidt 正交化過程得到[1]，系數(shù)c1，c2，…，cn由公式

給出.

2 結果證明

利用Moore-Penrose 求逆公式和Cramer 法則不難證明公式（11）和（13）.但是，為便于理解，這里給出其在現(xiàn)行的《線性代數(shù)》教科書和許多文獻中并不常見的直接證明.

用〈x，y〉表示Rm中向量x和y的Euclid 內積，表示向量x的范數(shù)；Im（G）和Ker（G）分別表示集合G 的值域和核.

引理1[4]設W 和Z 是Hilbert 空間.若算子G∈L（W，Z）和G*∈L（Z，W）相伴，則下列陳述成立：

（i）Im（G）=Z?存在γ＞0，使得

定理1的證明 因矩陣A可看作線性算子A∶Rm→Rn，即A∈L（Rm，Rn），故A的相伴算子A*∶Rn→Rm是A的轉置.對?b∈Rn，（1）有解的充分必要條件是算子A為滿射[5].由引理1 可知，存在γ＞0，使得‖A*z‖Rm≥γ‖z‖Rn（?z∈Rn）.因此，〈AA*z，z〉≥γ2‖z‖2Rn（?z∈Rn），這表明AA*是雙射.又因AA*是一n×n階實矩陣，故det（AA*）≠0.反過來，若det（AA*）≠0，即（AA*）-1存在，則對給定的b∈Rn，x=A*（AA*）-1b就是Az=b的一個解.

因z=（AA*）-1b是方程組（AA*）w=b的唯一解，故由定理1 可得

其中（AA*）j是將AA*的第j 個列向量用b=[b1b2…bn]T替換后所得到的矩陣.因此，（1）的解x=A*（AA*）-1b可寫成

的形式.此外，它還是最小范數(shù)解.事實上，若取w∈Rm使得Aw=b，則有

另一方面，

因此，‖w‖2-‖x‖2=‖w-x‖2≥0，即‖x‖≤‖w‖；特別地，當x＝w時，有‖x‖＝‖w‖.

的解.為此，令l1=[-1 -1 1 1]T，l2=[-1 1 -1 1]T，l3=[1 -1 -1 1]T，因 {l1，l2，l3} 在R3中正交，故（24）的解為x1=-1/4，x2=-1/4，x3=-1/4，x4=3/4.

3 變分解法

定理1 和定理2 雖然給出了（1）的最小范數(shù)解的公式，但它們并非求解的唯一途徑.下面介紹求解（1）的變分法，其解為二次函數(shù)j∶Rn→R，即

的最小值.

引理2[6]對給定的b∈Rn，線性方程組（1）有解x∈Rm的充分必要條件為

引理3若二次函數(shù)j 有最小值ξb∈Rn，則

是（1）的一個解.

注：實際上，（27）是j 有臨界點的最優(yōu)條件.同時，可以驗證由公式（27）和（9）給出的解完全一致.

定理3線性方程組（1）有解的充分必要條件是對?b∈Rn，二次函數(shù)j 有最小值.

證明 設（1）有解.因A是Rm到Rn的滿射，故由引理1 可知?γ＞0，使得‖A*ξ‖2≥γ2‖ξ‖2（ξ∈Rn）.于是因此，.這是j 存在最小值的保證.

下面給出一個不能應用定理1 和定理2，卻能應用引理2 的例子.