基于馳振的壓電能量采集器建模與實驗研究*

趙道利， 胡新宇， 孫維鵬， 郭鵬程

(西安理工大學省部共建西北旱區生態水利國家重點實驗室 西安，710048)

引 言

壓電能量采集器能把環境中的潛在能量(風能、振動能等)轉化為電能，適合為低能耗、工作環境惡劣的無線傳輸設備、微機電系統等供能。壓電能量采集器打破了傳統供能設備(化學電池)在壽命、使用范圍等方面的限制，在許多科技領域存在廣泛的應用前景[1-2]。根據能量轉換原理的不同，流致振動壓電能量采集器主要分為兩種:①基于渦激振動的壓電能量采集器較早得到研究，渦激振動的自限制特點有礙于更高能量的轉換；②基于馳振的壓電能量采集器具有較大的振幅，更有利于能量的有效開發[3]。

從Barrero等[4]提出關于馳振的能量采集概念開始，基于馳振壓電能量采集器的相關研究已取得諸多成果。在理論方面：Abdelkefi等[5-6]提出一種基于歐拉-伯努利梁理論的非線性機電耦合分布參數模型，并通過數值計算和實驗數據進行對比驗證，還通過該模型對不同形狀截面質量塊的能量采集器進行了模態分析，研究了質量塊截面形狀、風速以及外載荷對能量采集器性能的影響；Bibo等[7]建立了能量采集器的能量輸出和流速之間的普適性關系，這種關系有助于采集器性能的優化分析；Yan等[8]利用非線性機電耦合分布參數模型研究了從混合振動(馳振和基礎激勵)中獲取能量的概念，并探討了風速和基底加速度對能量采集器的影響；Tan等[9]針對懸臂式壓電能量采集器的分布參數模型提出一種機電解耦方法，便于確定各電元器件的最優值，從而實現最大收獲功率；唐浩俊等[10]基于馳振Den Hartog判據發展了馳振的能量分析方法，突破Den Hartog判據的局限性。在結構設計方面：文獻[11-12]提出一種單自由度壓電能量采集器，該能量采集器在5.2 m/s的風速下可以采集到大于50 mW的電能，足以為一些無線傳感設備供電，還采用線性和非線性的理論研究了特定形狀截面下的能量采集效果；Wang等[13]提出一種雙鉸鏈壓電片能量采集器模型并通過多種方法進行分析，發現該模型的振動頻率可調以方便適應周圍環境，而且其性能還可通過調節電路阻抗進行優化；Kwon[14]設計出能有效降低起振風速的“T”型懸臂梁式振動能量采集器；Liu等[15]研究了一種帶三刃“Y”型鈍體的懸臂梁式能量采集器，其能量輸出高于帶方柱的能量采集器，該結構在低風速下能有效激發馳振作用。除此之外：Zhao等[16]研究了3種不同形式的外接電路對基于馳振的壓電能量采集器性能的影響；Shen等[17]提出一種新型自供能振動阻尼技術，其具有較強的穩定性，可以為其他電路供電，可實現完全自供能；張軍等[18]進行了三棱柱的流致振動實驗，并對其能量轉化效率做出評估。

通過對各種文獻的總結發現，基于馳振的壓電能量采集器分布參數模型具有一定的局限性，不能實現對能量采集系統振動情況的分析。針對此缺陷，筆者對懸臂式壓電能量采集器的分布參數模型做出進一步的研究，得到質量塊起振風速以及能量采集器從起振到馳振過程中所采集到功率的解析解，并分別對正三棱柱和正四棱柱壓電能量采集器進行風洞實驗，將模型計算所得理論解和實驗值比對驗證了所得模型的合理性。此外，還通過變模型參數研究了不同截面形狀質量塊、質量塊質量、風速和外載阻值對能量采集系統的影響。

1 理論建模

筆者所研究的懸臂式壓電能量采集裝置由懸臂梁、壓電纖維片(macro fiber composite，簡稱MFC)和質量塊組成，MFC貼在懸臂梁左側表面，懸臂梁上端與連接桿連接，下端連接質量塊。圖1為懸臂式壓電能量采集裝置示意圖，懸臂梁的厚度方向為x向，寬度方向為y向，長度方向為z向。作為能量采集器的換能部件，質量塊在激勵下不產生形變，所以在模型分析中對質量塊作理想剛性體處理。在某一時刻t時，速度為v的流體從y方向流經質量塊，質量塊因流體繞流作用在x方向上發生雙向擺動，懸臂梁和MFC在質量塊的帶動下產生周期性形變，MFC因形變而產生電能，其中質量塊的模態位移坐標為q(t)，MFC產生的電壓值為U(t)。

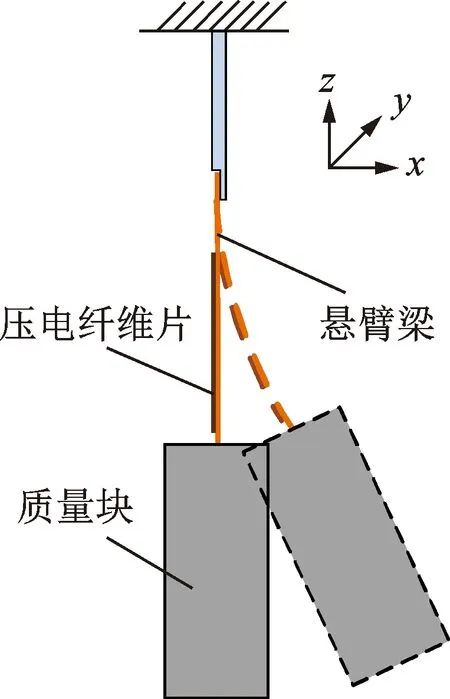
圖1 懸臂式壓電能量采集裝置示意圖Fig.1 Schematic diagram of cantilever piezoelectric energy harvester

根據Abdelkefi等[6]提出的壓電能量采集器分布參數模型，將其降階可以得到簡化后的機電控制方程為

其中：ξ為機械阻尼系數；ω為能量采集系統的1階固有頻率；θp=(φ′(L2)-φ′(L1))?，為壓電耦合項，其中φ(x)為懸臂梁的1階模態振型，L1為懸臂梁上端到MFC起始端的距離，L2為懸臂梁上端到MFC末端的距離，?為壓電耦合系數；f(t)為1階氣動力；Cp為MFC的電容項；R為能量采集系統的外載阻值。

根據Abdelkefi等[6]提出的氣動馳振模型可得到馳振作用下的1階氣動力f(t)為

(3)

其中：a1,a3為氣動力經驗系數，由實驗確定；ρair為空氣密度；btip為質量塊寬度，即迎風面寬度；k1,k3為氣動力系數。

k1,k3的具體表達式為

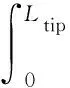
(4)

其中：L為懸臂梁長度；Ltip為質量塊長度。

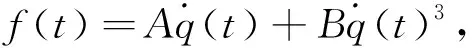
(5)

在能量采集過程中，質量塊的振動頻率和能量采集器的輸出電壓頻率相同，所以對q(t)和U(t)作如下假設

(6)

其中：q0和U0分別為模態坐標位移的振幅值和輸出電壓幅值；Ω為頻率；α為相位差。

將式(6)分別帶入式(2)中，且必須滿足在任何時間下的有效性，可得

消掉式(7,8)中的α，得到U0和q0的關系為

(9)

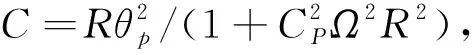
將式(7,8)代入式(6)，消去三角函數可以得到

(10)

將式(10)代入控制方程(1)中可以得到解耦后的控制方程

(11)

其中頻率滿足下面式子

(12)

(13)

由式(9)和式(13)可得

(14)

由式(14)可知，當A-2ξω-C<0時，系統處于穩定狀態，質量塊不產生位移。令A-2ξω-C=0，可以得到系統的起振風速為

v0=2(2ξω+C)/a1ρairbtipk1

(15)

當vv0時，質量塊振動，壓電能量采集器的采集功率P分別為

(16)

2 實驗風洞及測試系統

為了驗證上述模型的準確性，利用如圖2所示的懸臂梁式壓電能量采集器進行風洞實驗。MFC用環氧樹脂膠黏劑黏貼在懸臂梁表面，懸臂梁下端安裝質量塊。本次實驗所用質量塊分別是截面形狀為正三角形的三棱柱和正方形的四棱柱，質量塊的側面作為迎風面，實驗時迎風面垂直于來流方面，如圖3所示。為保證實驗結果之間的有效對比分析，質量塊的重量、高度和迎風面寬度相同，懸臂梁、MFC以及質量塊的具體幾何尺寸和物理參數如表1所示。

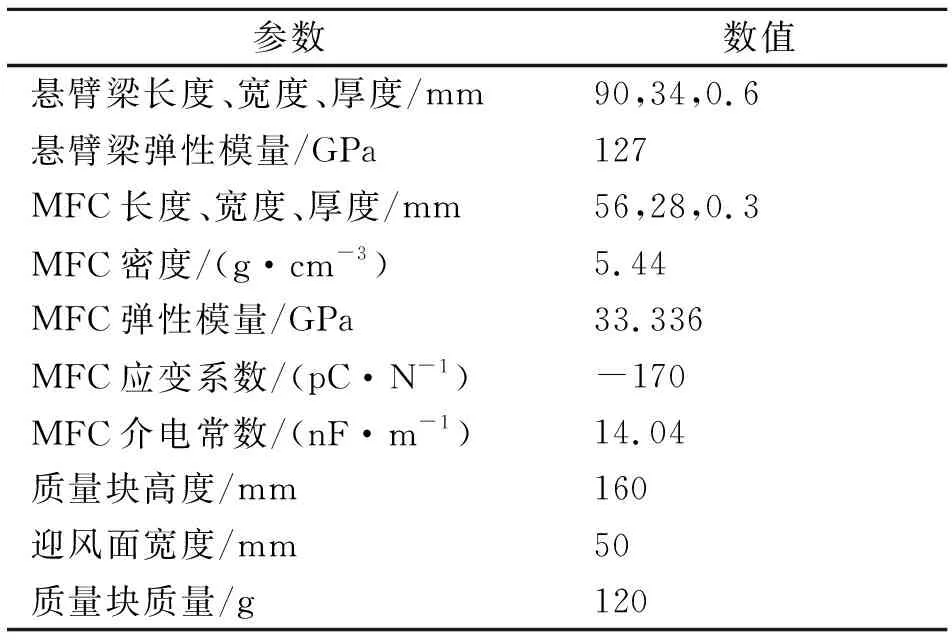
表1 懸臂梁、MFC和質量塊的幾何尺寸和物理參數

圖2 懸臂梁式壓電能量采集器Fig.2 Cantilever piezoelectric energy harvester

圖3 質量塊截面形狀示意圖Fig.3 Schematic diagram of cross-section shape of bluff body

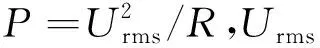
實驗是在直流式閉口低速風洞中進行的，該風洞由5個主要部件構成，分別為穩定段、收縮段、實驗段、擴散段和風機，如圖4所示。穩定段安裝有阻尼網和蜂窩器，流體流經穩定段能有效降低測試流體的湍流度。收縮段用于增加測試流體的速度，擴散段再降低其出口速度。實驗段位于風洞中間位置，有效實驗空間的長度為1.8 m，寬度為0.85 m。實驗段前端頂部安裝有分體式風速儀，用來測量流體速度。當風機達到最大轉速時，風洞內的測試流體速度能達到25 m/s。

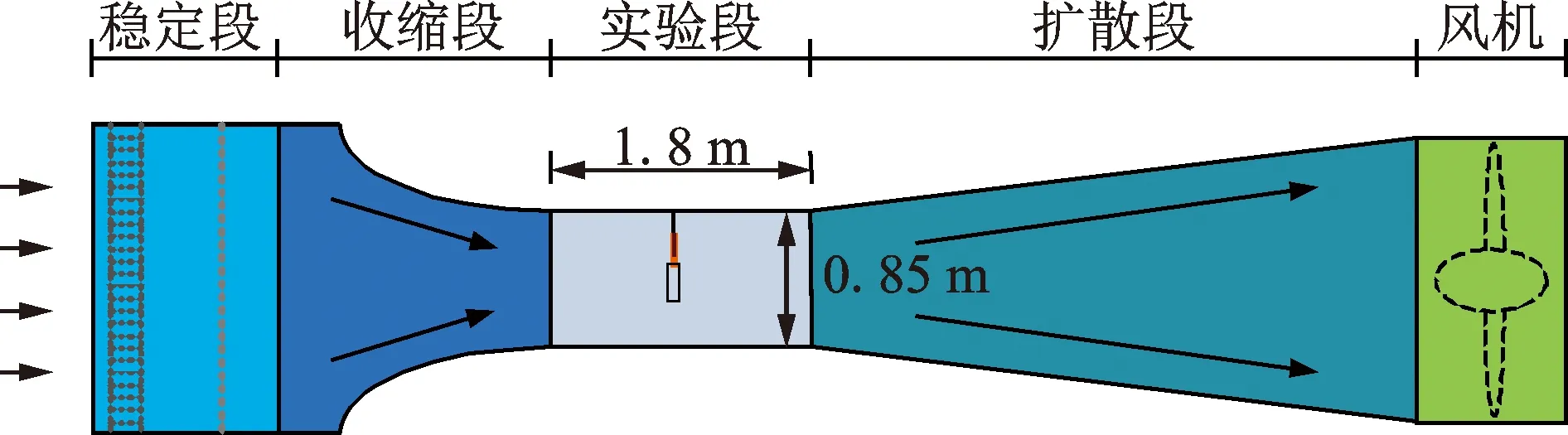
圖4 直流式閉口低速風洞示意圖Fig.4 Schematic diagram of closed direct-flow low-speed wind tunnel

實驗在接近常溫常壓的條件下進行，測試風速從0開始到20 m/s結束，氣體流動區域的雷諾數處于0～6.73×104之間，測試風速間隔為1 m/s，單個風速下測試時間不少于5 min。實驗測試區域的阻塞比為1.36%，相對來說非常小，而且風洞內壁相對光滑，邊界層厚度可以忽略，可視為滑移邊界，不會對實驗測試造成嚴重影響。當氣體經過穩定段時，實驗段入口流速和湍流強度均可實現垂直(與風洞縱截面)分布。

3 結果和分析

3.1 實驗結果和模型驗證

通過風洞實驗發現，正三棱柱和正四棱柱質量塊的起振風速v0均約為2 m/s。當風速比較小時，質量塊所受氣動升力較小不足以克服系統阻尼力，系統處于穩定狀態；當風速超過2 m/s時，氣動力得到提升致使質量塊起振，風速再逐漸增加，正三棱柱和正四棱柱能量采集器的振動幅度均有明顯的增加，說明了所測試能量采集器的馳振特征。兩種質量塊的流致振動頻率基本穩定，更有利于為外部設備供能。通過計算可以得到理論模型中的相關參數，其中正三棱柱能量采集器的氣動力經驗系數a1和a3分別為2.846 3和-46 000；正四棱柱能量采集器的氣動力經驗系數a1和a3分別為3.098 5和-31 000。

圖5是流速分別為4，9和17 m/s時，由式(1)和式(2)解得的電壓數值解和實驗所得電壓時程曲線之間的對比。從圖中的實驗值可以看出：相同流速下，正四棱柱能量采集器的輸出電壓幅值比較大；隨著風速的增加，實驗所得輸出電壓逐步增大，但是較小風速下所得實驗電壓時程曲線不同時刻幅值的差距較小，波形更穩定一些。通過對模型解和實驗值的對比分析發現，模型結果與實驗結果相吻合。

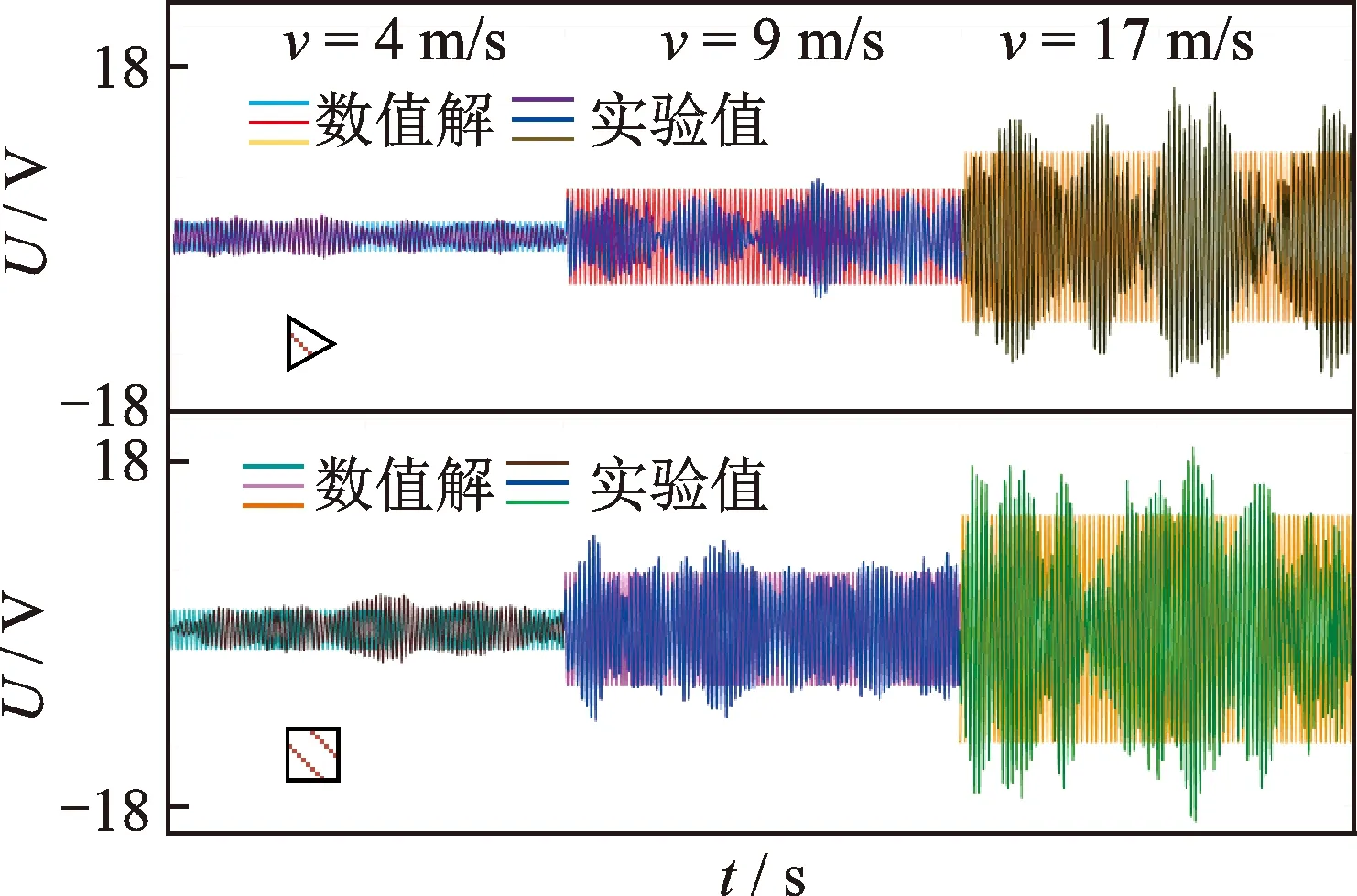
圖5 理論解和實驗所得電壓時程曲線對比Fig.5 Comparison of time history of voltage between theoretical solution and experimental values

圖6為不同質量塊能量采集器采集功率的實驗值和式(16)得到的解析解對比。從實驗結果可以看出：采集功率均隨風速的增加而增大，而且其增加幅度也有所提高；從采集到的能量大小來看，正四棱柱能量采集器的采集效果要優于正三棱柱能量采集器，且在風速增加的過程中，不同質量塊能量采集器采集電壓之間的差距拉大，風速達到20 m/s時，前、后者的采集功率分別達到0.248 5 和0.125 9 mW。從式(16)可以看出，采集功率和氣動力經驗系數a3成反比，但是和氣動力經驗系數a1成正比，所以a1/a3值越大，能量采集器的采集功率越大。從理論計算得出，正四棱柱能量采集器的a1/a3絕對值較大，所以正四棱柱能量采集器的采集效果較好。通過實驗值和數值解的對比，實驗值和解析解之間的吻合度較高，所建理論模型具有較高的精度，能有效分析懸臂梁式壓電能量采集器的振動和能量輸出情況，滿足類似能量采集系統的性能預估。

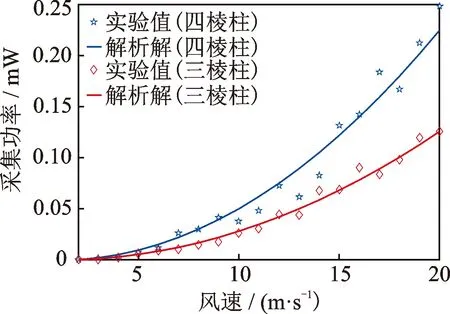
圖6 采集功率實驗值和解析解對比Fig.6 Comparison of harvested power between experimental values and analytic solution

為了對壓電能量采集器進行更深入的研究，選取幾種結構類似的能量采集器作性能對比，并分析它們之間的優缺點。Akaydin等[19]對繞流體為圓柱的能量采集器進行研究，該采集器在0～12m/s風速范圍內的最大采集功率密度為18.1μW/cm3，而筆者所研究的采集器在相同風速范圍內的最大功率密度達到39.4μW/cm3，說明馳振作用更有利于能量采集。Zhou等[20]研究了鈍體的顫振和磁效應雙重作用下的能量采集器，但是其最大采集功率密度只達到3 μW/cm3，而筆者所研究的采集器在相同風速下的功率密度能達到15.8μW/cm3，前者所設計的采集器未能真正激發流致振動作用，致使采集能量較低。但是相比于Kwon[14]提出的“T”型能量采集器以及Liu等[15]提出的“Y”型質量塊能量采集器，本研究中能量采集器的采集性能還有一定差距，其主要原因有：質量塊的馳振效果不及“T”型和“Y”型；懸臂梁尺寸并不能最大程度帶動壓電片進行形變，所以對于所研究的能量采集器還需進行結構尺寸和質量塊的進一步優化。

3.2 系統性能預估

圖7為v=20 m/s時不同質量正三棱柱和正四棱柱能量采集器的采集功率隨外載電阻值的變化。如圖所示，在同等條件下，正四棱柱能量采集器的采集性能比正三棱柱能量采集器的更優。質量塊質量和外載電阻的選取對能量采集器的性能有較大的影響，對于不同條件下的能量采集器均存在最優外載阻值，并非電阻值越大或越小采集器采集效果最好，但是質量塊的質量越小，采集器的性能越佳。對于外載電阻比較大(R>2×106Ω)的系統，質量塊質量的改變對系統采集性能幾乎沒有影響；但是對于外載電阻比較小(R<2×106Ω)的系統，質量塊質量越大，采集器的采集效果就會變弱。所以對于質量塊質量易受外部環境影響的采集器，在達標的條件下使用較大阻值的外載電阻能使系統更穩定。

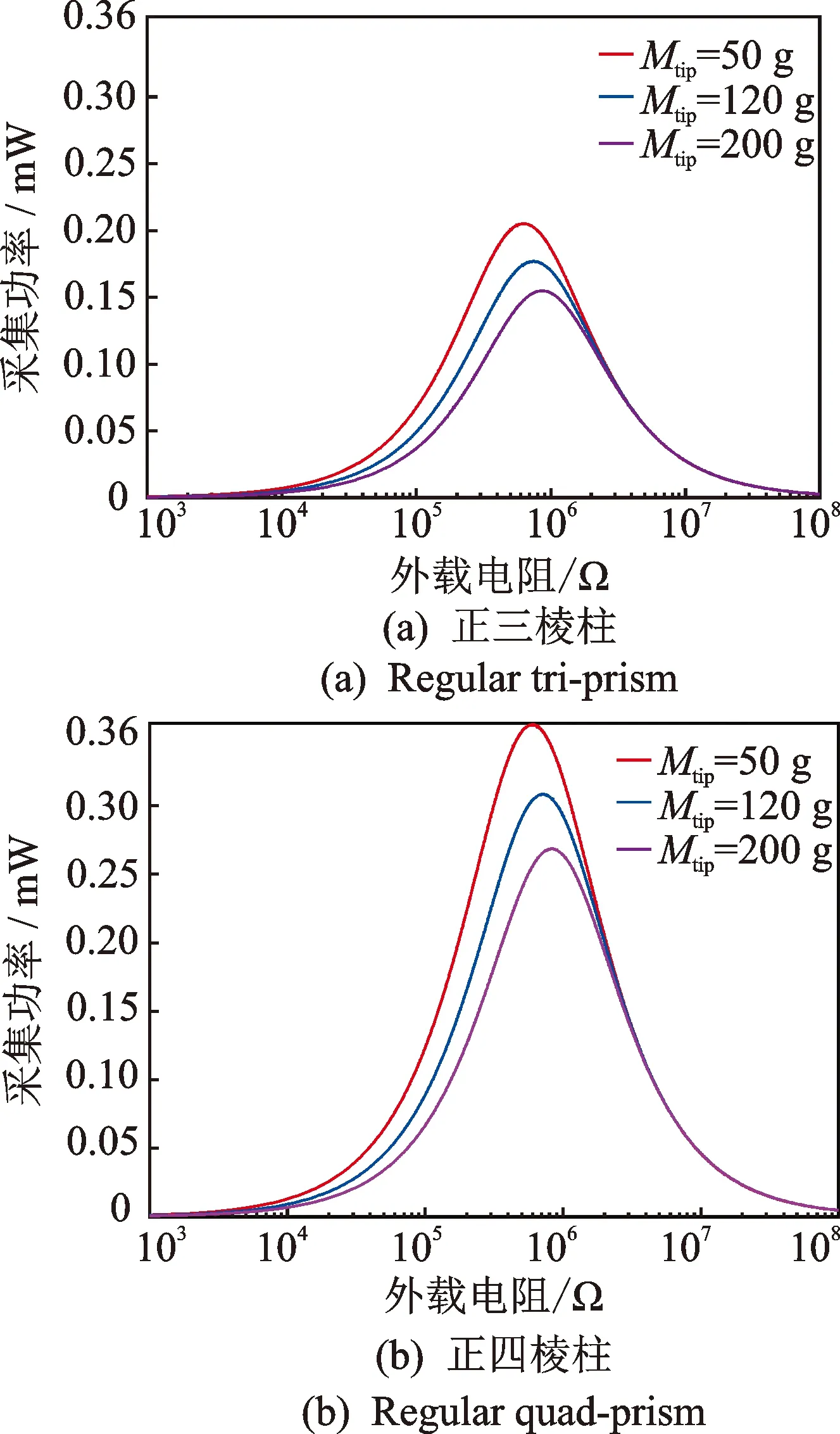
圖7 v=20 m/s時不同質量塊能量采集器采集功率隨外載阻值的變化Fig.7 Harvested power of the energy harvester varied with load resistances for different tips mass at v=20 m/s

圖8為不同風速下正三棱柱和正四棱柱能量采集器的采集功率隨外載電阻值的變化。從圖中可以看出，在同等條件下，正四棱柱能量采集器的采集效果優于正三棱柱能量采集器。風速增加時，采集功率逐漸增大，兩種能量采集器的最優外載阻值均會略微減小。當達到最大風速時，正四棱柱和正三棱柱能量采集器的采集功率分別可以達到0.308 3 和0.176 9 mW。當采集器的外載阻值越靠近最優阻值(2×104～2×107Ω區間)時，風速的變化對采集器能量輸出的穩定性產生較大影響，但風速越大采集到的功率反而越大。因此對于風場不穩定的情況，外載阻值應選取比最優阻值更大或更小的，必要時還需得到外部電路的修正。對于較小的流速(從開始起振到3.7 m/s的風速范圍內)，不同質量塊能量采集器均出現雙最優阻值，如圖8中的小圖所示。

4 結束語

筆者在懸臂式壓電能量采集器分布參數模型的基礎上，對馳振作用下能量采集器的振動和能量采集情況進一步分析，得到質量塊起振風速以及從起振到馳振過程中所采集到的功率解析解。建立懸臂式壓電能采集器實物模型，并通過風洞實驗對其進行測試，發現正三棱柱和正四棱柱能量采集器的起振風速基本相同，但正四棱柱能量采集器的能量采集功率效果要優于正三棱柱能量采集器，當風速達到20 m/s時，其采集功率分別達到0.248 5 和0.125 9 mW。通過對模型求解和實驗所得功率、電壓時程曲線的對比發現，實驗值和理論解之間很好吻合，證實了所建模型的正確性，并選取了類似結構采集器進行了優缺點分析。利用理論模型對能量采集器的性能進行了預估，分析發現：風速越大，質量塊質量越小，能量采集器采集功率越高，而且風速和質量塊的變化也會對采集器最優外載阻值產生影響；采集功率隨外載阻值的增大均呈現先增大后減小的情形，對于不同條件下的能量采集器均存在最優外載阻值，低風速下還會出現雙最優阻值。