軸向預壓縮雙晶片動力學模型與特性分析*

陳 恒， 陳 超， 劉士祥， 程 罡

(南京航空航天大學機械結構力學及控制國家重點實驗室 南京，210016)

引 言

壓電雙晶片具有結構簡單、質量輕、帶寬高等優點，但由于壓電陶瓷本身的激勵應變小[1]，一般只有幾百個微應變，因此壓電雙晶片存在輸出位移小的缺點。傳統上需要設計機械式的位移放大機構放大雙晶片的輸出位移，但這卻在一定程度上降低了雙晶片的輸出力[2-4]。針對這一問題，Lesieutre等[5]提出了后屈曲預壓縮(post-buckled pre-compressed，縮寫為PBP)的概念，通過理論分析及實驗得出的結論表明，對雙晶片施加軸向預壓力能夠同時提高其力與位移輸出能力，顯著提高雙晶片的機電轉換效率。理論上當軸向預壓力達到雙晶片的一階屈曲臨界載荷時，雙晶片的機電耦合系數將達到1[6]。基于這一原理，國外的學者們將預壓縮雙晶片應用于多種飛行器舵機的設計與應用中，并取得了一系列的成果[7-11]。

為了分析雙晶片在軸向壓力下的靜、動態特性，Giannopoulos等[12-13]利用非線性力學的方法建立雙晶片的理論模型，并進行了雙晶片在不同軸向力下的靜變形實驗。Giannopoulos由經典層合板理論給出軸向受壓雙晶片的平衡方程，將雙晶片的撓度展開為傅里葉級數的形式(即假設撓度為各階屈曲模態的線性疊加)，給出雙晶片的總勢能，利用最小勢能原理及拉格朗日乘子法求解出特定邊界條件下傅里葉級數中的各階未知系數，從而得到雙晶片在軸向力及電壓作用下的靜撓度表達式，并通過實驗和ANSYS軟件驗證了分析模型的正確性。

基于PBP概念的壓電雙晶片作為飛行器舵機的驅動部件，其性能對舵機性能有著至關重要的影響。因此，有必要確切地描述雙晶片在軸向預壓力下的靜、動態性能。2005年，Ron Barrett團隊將PBP作動器應用于自主式飛行器時，通過將壓電產生的效應等效為簡支梁兩端的彎矩建立了雙晶片的靜力學模型，該模型得到了雙晶片發生靜變形的解析表達式[9]。2007年，該團隊又將雙晶片應用于機翼的飛行控制中，同時建立了雙晶片的動力學模型。 該模型將雙晶片化為單自由度系統，通過假設形狀函數，帶入動能、勢能和功的表達式，利用Lagrange原理得到壓電雙晶片的模態方程，然后通過系統的等效剛度和質量來求得雙晶片的一階固有頻率[11]。這些方法雖然可以得到系統的靜、動態特性，但卻無法用一個表達式來描述雙晶片的所有模態，使雙晶片的各階模態較為直觀地顯現出來。筆者通過推導雙晶片各層的應變能、動能、電勢能和外部力的描述，將力和電的作用納入到統一的框架中，得到系統關于中性層撓度的泛函表達式，再通過Hamilton原理得到軸向預壓縮條件下雙晶片的動力學方程與特定的邊界條件。通過求解偏微分方程不僅得到系統的靜變形，同時得到了雙晶片關于各階頻率和陣型的解析解表達式，并對系統的動力學特性進行了分析。

1 壓電雙晶片的機電耦合模型

1.1 動力學方程的建立

舵機用雙晶片模型如圖1所示。雙晶片一端固定鉸支，一端可沿軸向滑動，舵片與固定鉸支端固連，通過給雙晶片施加電壓帶動舵片旋轉。

圖1 預壓縮雙晶片的驅動原理Fig.1 Driving principle of axial pre-compressed piezoelectric bimorph

Hamilton原理是以變分為基礎的建模方法，常用來建立連續質量分布和連續剛體分布系統(彈性系統)的動力學模型。壓電雙晶片可以簡化為一個3層的壓電層合板，具有力和電場的耦合作用，對于這樣無限自由度的機電耦合系統應采用能量法較為簡便。因為雙晶片的變形量較小，基于歐拉梁的假設，忽略微元轉動的基體動能[14]

(1)

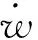
同理，壓電陶瓷層的動能為

(2)

其中：下標p表示壓電陶瓷。

基體的純彎曲應變能為

(3)

其中：Es為基體的彈性模量；Is為基體的截面慣性矩；w″為中性層撓度對坐標軸x的二階導數。

壓電陶瓷層的應變能為

(4)

為了得到壓電陶瓷片應變能關于雙晶片中性層撓度的表達式，可由壓電方程得到壓電層應力、應變及外部電場強度的關系，并通過梁的幾何方程得到應變與梁的彎曲曲率之間的關系，而由小變形假設可以將曲率近似為撓度對x軸的二階導數，由此可得以撓度為自變量的壓電陶瓷層應變能泛函。已知d型壓電本構方程為

s=SET+dTE

(5)

D=dT+εTE

(6)

其中：s為應變向量；SE為柔度矩陣；d為壓電常數矩陣；E為外加電場向量；D為電位移向量；T為應力向量；εT為介電常數矩陣。

由歐拉梁的基本假設，忽略剪切變形，雙晶片外部電場只有E3≠0。因此有

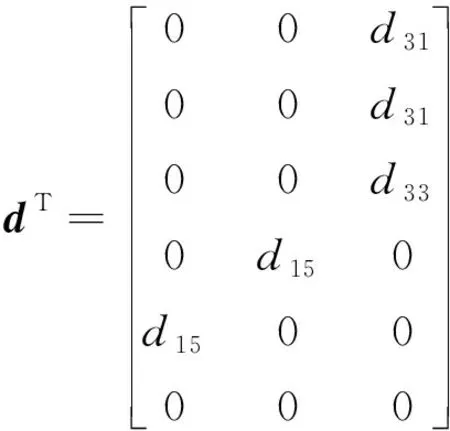
(7a)

(7b)

(7c)

由于在歐拉梁假設下的正應力僅σx≠0，并由式(5)、式(7)可得壓電梁壓電陶瓷層的應變向量

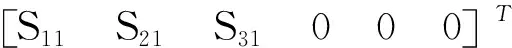
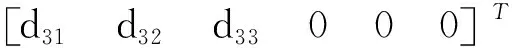
(8)

由式(8)得到壓電陶瓷層x向正應變為

sx=S11σx+E3d31

(9)

然后得到x向正應力為

(10)

其中：Ep為壓電陶瓷在1方向的彈性模量，大小為柔度S11系數的倒數。

每片壓電陶瓷的彎曲應變能為

(11)

其中：h為厚度；b為雙晶片的寬度。

將式(10)代入式(11)可得

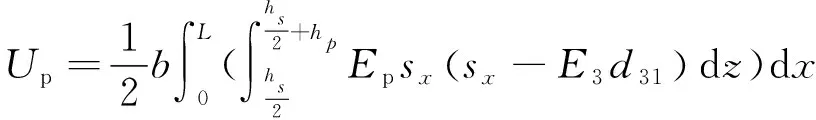
(12)

已知梁彎曲的小變形幾何方程為

sx=-zw″

(13)

將式(13)代入式(12)，得到關于中性層撓度的壓電陶瓷層應變能表達式為

(14)

由式(14)及式(3)可以得到壓電陶瓷層的截面慣性矩為

(15)

為了得到壓電陶瓷層關于撓度的電勢能泛函

(16)

由式(6)、式(7)、式(10)和式(13)可得

(17)

積分后可得

(18)

其中：E3為z向電場強度。

E3與壓電陶瓷層的外加電壓伏值V之間的關系為

E3=V/hp

(19)

F為軸向壓力，假設其方向沿x軸負方向，小變形假設下近似為

(20)

整個雙晶片的動能、勢能以及外部作用為

(21)

其中：下標bi表示壓電雙晶片。

由哈密頓原理，通過求泛函的駐值

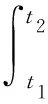
(22)

得到關于中性層撓度的偏微分方程。可以看出，雙晶片的動力學方程與普通均質梁具有同樣的形式，逆壓電效應沒有體現在方程中而是在邊界條件里

(23)

可得到簡支邊界條件為

(24)

1.2 雙晶片驅動器的動力學特性

通過分離變量法可將前面描述驅動器的力學偏微分方程分解為兩個常微分方程，由具體的邊界條件得到關于頻率的線性方程組。令該方程組的系數矩陣行列式為零，可解出驅動器在特定邊界條件下的固有頻率，并通過求解方程組對應的齊次方程得到系統的固有振型。假設外加電場為簡諧激勵形式，從上述偏微分方程可求解得到驅動器的穩態響應[15]。利用該方法得到雙晶片簡支條件下的固有頻率與固有振型的解析表達式如下。

固有頻率為

(25)

固有振型為

(26)

為了得到雙晶片在簡諧激勵下的響應，令外加電壓為

V=vsin(ωt)

(27)

不考慮阻尼，可假設雙晶片的響應為

w=φ(x)sin(ωt)

(28)

將式(28)代入式(23)及邊界條件(24)中解得

φ(x)=aTb

(29)

其中

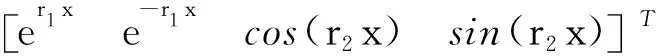
(30)

(31)

(32)

(33)

1.3 雙晶片驅動器的靜態特性

為了得到驅動器的靜態特性，只需將動力學方程中的加速度項為零，即可得到描述該機電耦合系統靜態特性的微分方程，然后可求解得到雙晶片在不同電壓、軸向預壓力下的靜態輸出特性。

由式(23)得到靜態撓度方程為

EIw(4)+Fw″=0

(34)

其通解為

(35)

由式(24)、式(34)得

(36)

通過求解上述矩陣方程可得到邊界條件式(24)下驅動器的靜變形為

(37)

簡支條件下雙晶片輸出軸轉角，即x=0處轉角為

(38)

簡支的雙晶片滑動端x向位移為

(39)

由式(25)令ω1=0，得到簡支雙晶片的一階屈曲臨界載荷為

(40)

2 雙晶片的有限元分析

通過以上分析建立了描述軸向預壓縮雙晶片的動力學方程，從其動力學方程及邊界條件中得到靜撓度、輸出轉角、固有頻率及固有振型等的解析解。

作為比較，利用ANSYS軟件對雙晶片進行有限元分析，雙晶片的幾何尺寸及材料屬性由表1給出。壓電陶瓷的剛度系數矩陣(單位為GPa)如下

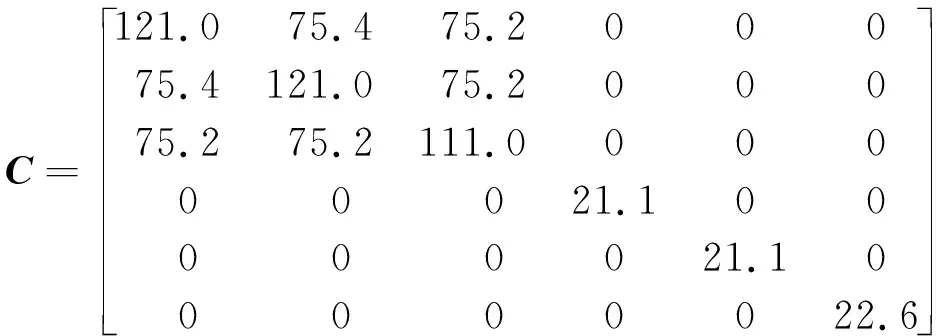
(41)

2.1 驅動器的靜態特性

根據表1中的數據，分別對雙晶片施加不同的電壓和0.05倍～0.85倍屈曲臨界載荷的軸向力，并利用上節中的理論分析得到相應的結果。同時利用ANSYS軟件進行靜力學分析，壓電陶瓷層選用solid226單元類型，基體選用solid186單元，在分析設置中打開大變形選項。設壓電陶瓷的壓電應力系數e33=e15=0，已知d31可從陶瓷層的剛度系數矩陣求出對應的e31=-30.217 2 C/m2。

從模型計算得到雙晶片的一階屈曲臨界載荷Fcr=96.97N。對于簡支雙晶片一般把固定鉸支端作為輸出軸，通過輸出軸的轉動驅動舵面偏轉。由于ANSYS不能直接計算出雙晶片的固定鉸支端轉角，可從ANSYS計算結果中提取距離固定端1mm處的撓度w，則雙晶片的輸出轉角近似為θ=arctan(1 000w)。式(37)、式(38)得到的結果與ANSYS計算結果如圖2、圖3所示，橫坐標為按屈曲臨界載荷歸一化的軸向力，縱坐標為雙晶片的最大撓度與最大轉角。

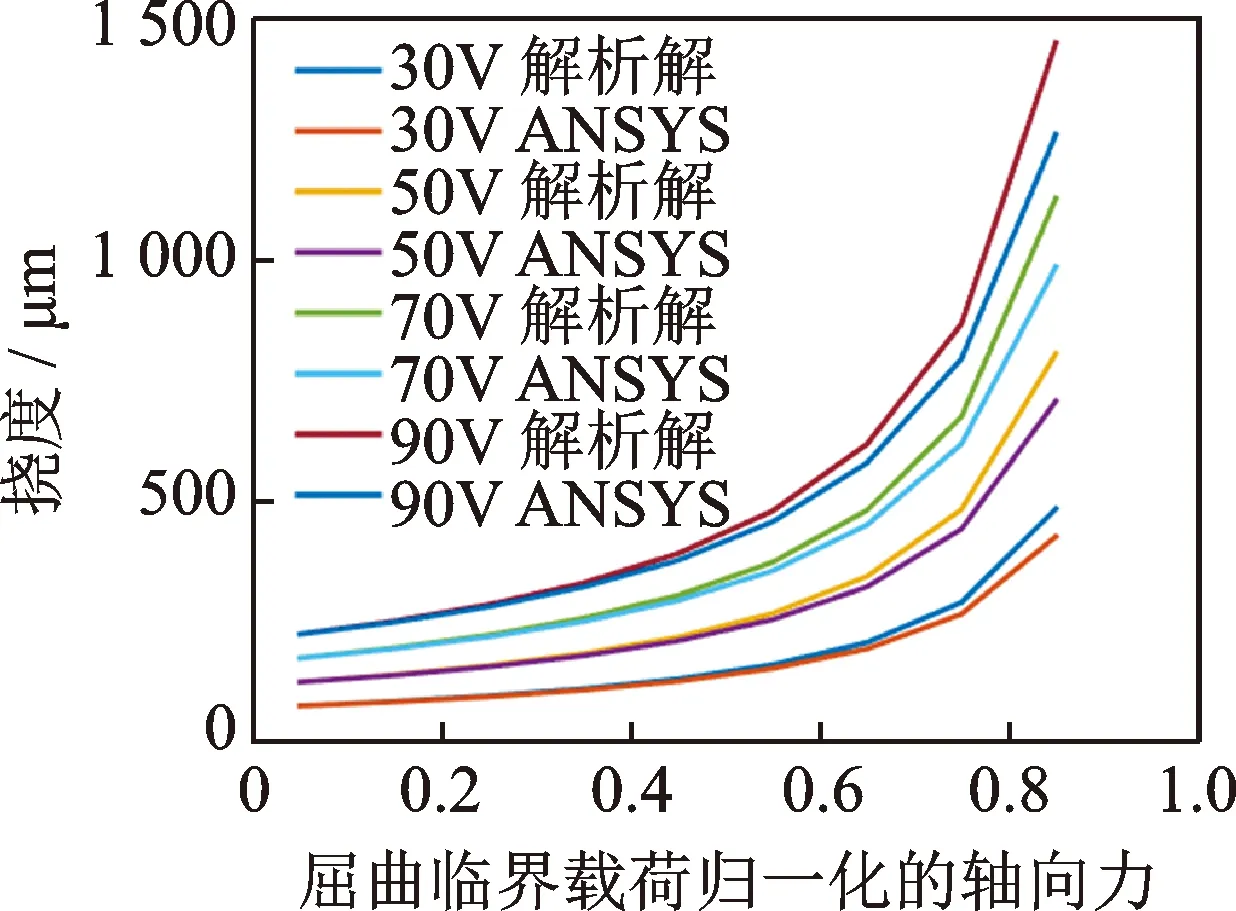
圖2 不同電壓下軸向力與雙晶片最大撓度的關系Fig.2 Relationship between the deflection and the axial force at different voltages

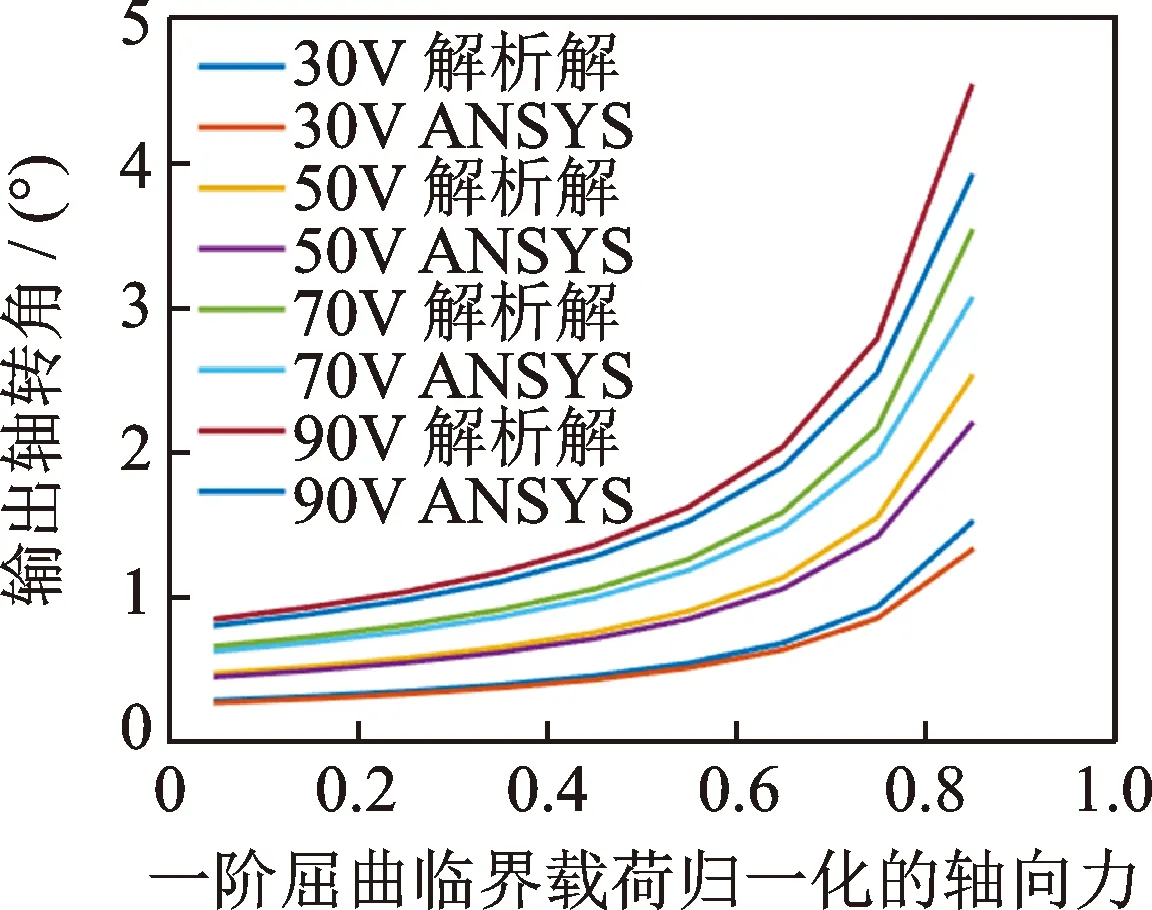
圖3 不同電壓下軸向力與雙晶片輸出轉角的關系Fig.3 Relationship between the output angle and the axial force at different voltages

從圖2、圖3中的結果可以看出，ANSYS計算結果模型與解析解計算結果趨勢上基本一致。小軸向力下兩者相差很小，由于本研究的理論模型采用了小變形假設，隨著軸向力的增大計算誤差會越來越大，但趨勢是一致的。另外，理論模型中近似地認為沿壓電陶瓷厚度方向電場強度均勻分布也會引起一定的誤差。增大軸向力對雙晶片的輸出位移有明顯的放大作用。為了給預壓力施加部分的結構設計提供理論依據，圖4給出簡支雙晶片滑動端x向位移的計算結果。

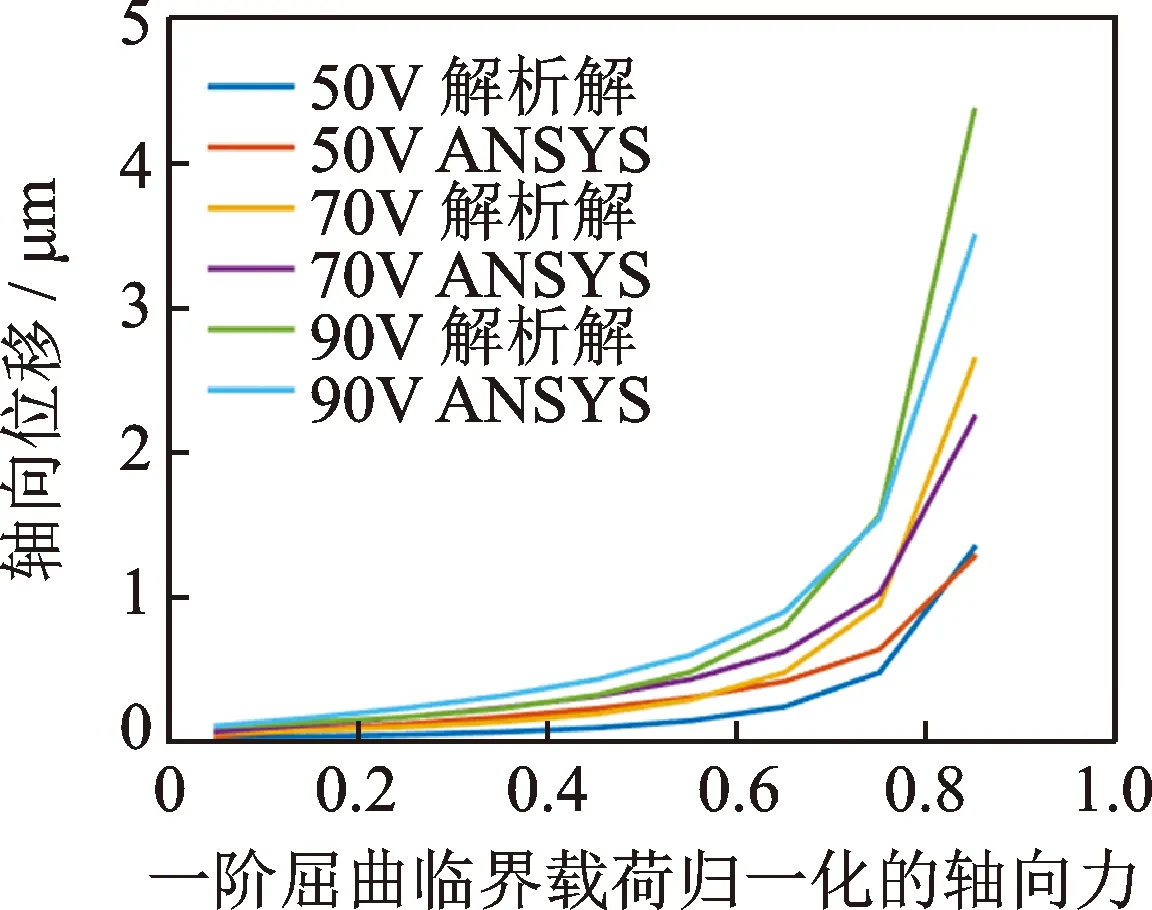
圖4 簡支雙晶片的軸向剛度特性Fig.4 Axial stiffness characteristics of the Bimorph

從圖4可以看出，簡支雙晶片的軸向剛度在0～0.4倍的屈曲臨界載荷下基本呈線性，在大軸向力下呈明顯的非線性，隨著軸向力的增大，雙晶片剛度漸軟，理論上當軸向力達到屈曲臨界載荷時雙晶片的軸向剛度將為零。

從上面的仿真結果可以看出，軸向力對雙晶片的靜態位移輸出能力有明顯的放大作用，較大軸向力下雙晶片的軸向剛度呈現明顯的非線性。通過與ANSYS計算結果的比較也證實了本研究的理論分析結果在較小軸向力下是基本正確的，大軸向力下(接近屈曲臨界載荷)理論計算結果與ANSYS仿真結果趨勢上基本一致。

2.2 驅動器的動力學特性

通過模型的理論分析給出了在軸向力及電壓的作用下雙晶片的結構動力學特性表達式，得到了簡支邊界條件下雙晶片的固有頻率、固有振型及幅頻特性的解析表達式。通過式(25)計算出雙晶片的固有頻率，并與ANSYS預應力模態分析結果放在一起進行比較，在ANSYS軟件靜力學分析設置中打開大變形選項，結果如圖5所示。

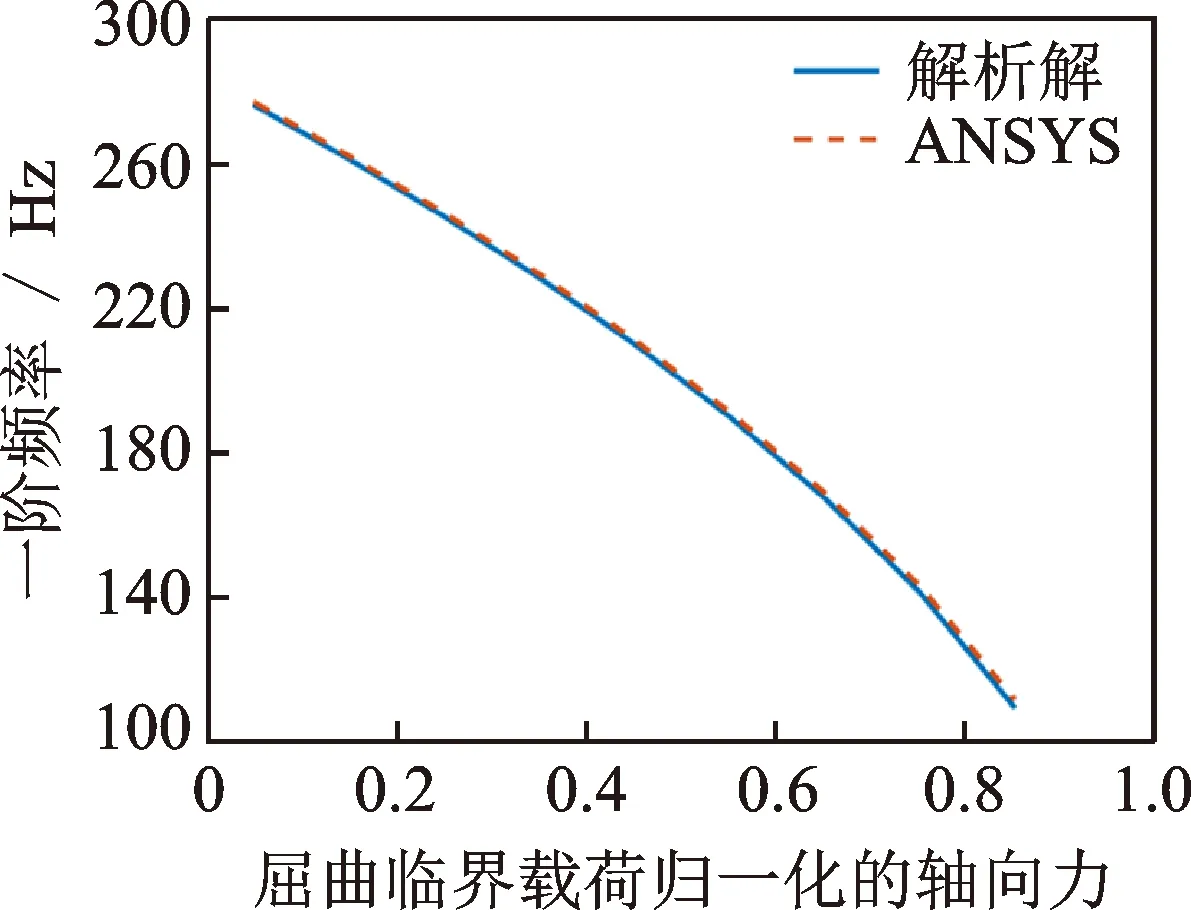
圖5 與簡支雙晶片一階彎振頻率的關系Fig.5 Relationship between 1st bending frequency and the axial force at different voltages

在式(29)～(33)中，令x=L/2，計算出雙晶片的穩態響應與ANSYS預應力下諧響應計算結果如圖6所示。在ANSYS中進行有預應力的諧響應分析，首先，進行靜力學分析計算結構的預應力，添加鉸支邊界條件，在滑動鉸支端對雙晶片施加軸向力，分析設置中打開大變形選項；其次，將靜力學分析的結果導入模態分析，通過模態疊加法進行諧響應分析。諧響應分析中，在雙晶片兩端施加等效彎矩(相當于施加1V電壓引起的彎矩)，計算得到簡支雙晶片在不同軸向力作用下的幅頻特性曲線。

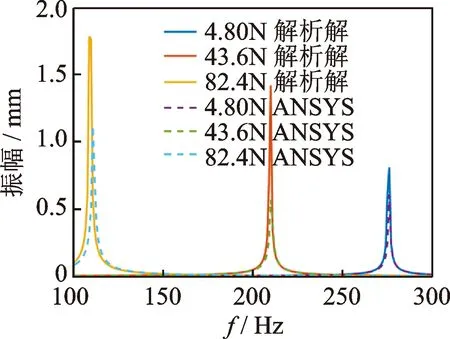
圖6 簡支雙晶片1V電壓下的幅頻特性Fig.6 Amplitude-frequency characteristics of bimorph under 1V voltage

3 可調軸向預緊力的雙晶片實驗研究

3.1 雙晶片的靜態實驗

為了測試舵機用雙晶片的靜態特性，設計并制作出實驗裝置如圖7所示。雙晶片左側嵌入到固定鉸支端即輸出軸上，右側嵌入到滑動鉸支端，滑動端與底座上的導軌相連，通過砝碼給雙晶片施加軸向力，利用激光位移傳感器測量雙晶片中點撓度。通過給雙晶片施加直流電來測試雙晶片的靜態撓度，實驗結果與解析解計算結果如圖8所示。從圖中可以看出，軸向力在一定程度上能夠放大雙晶片的輸出位移,而且雙晶片的撓度對電壓有較好的線性度。

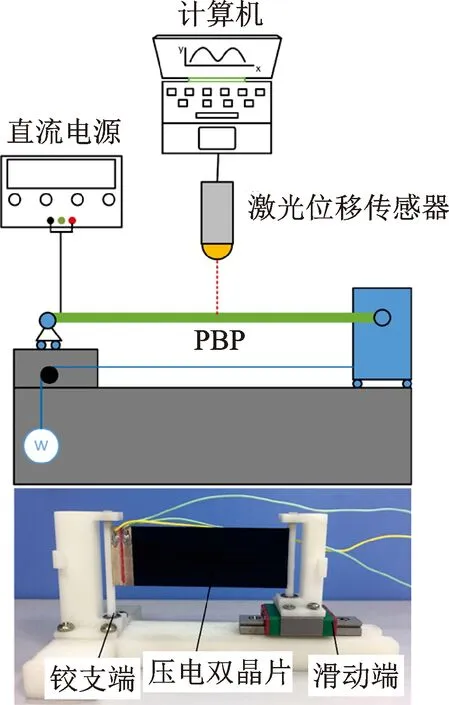
圖7 軸向預壓縮簡支雙晶片實驗裝置Fig.7 Experimental device for axial pre-compressed piezoelectric bimorph

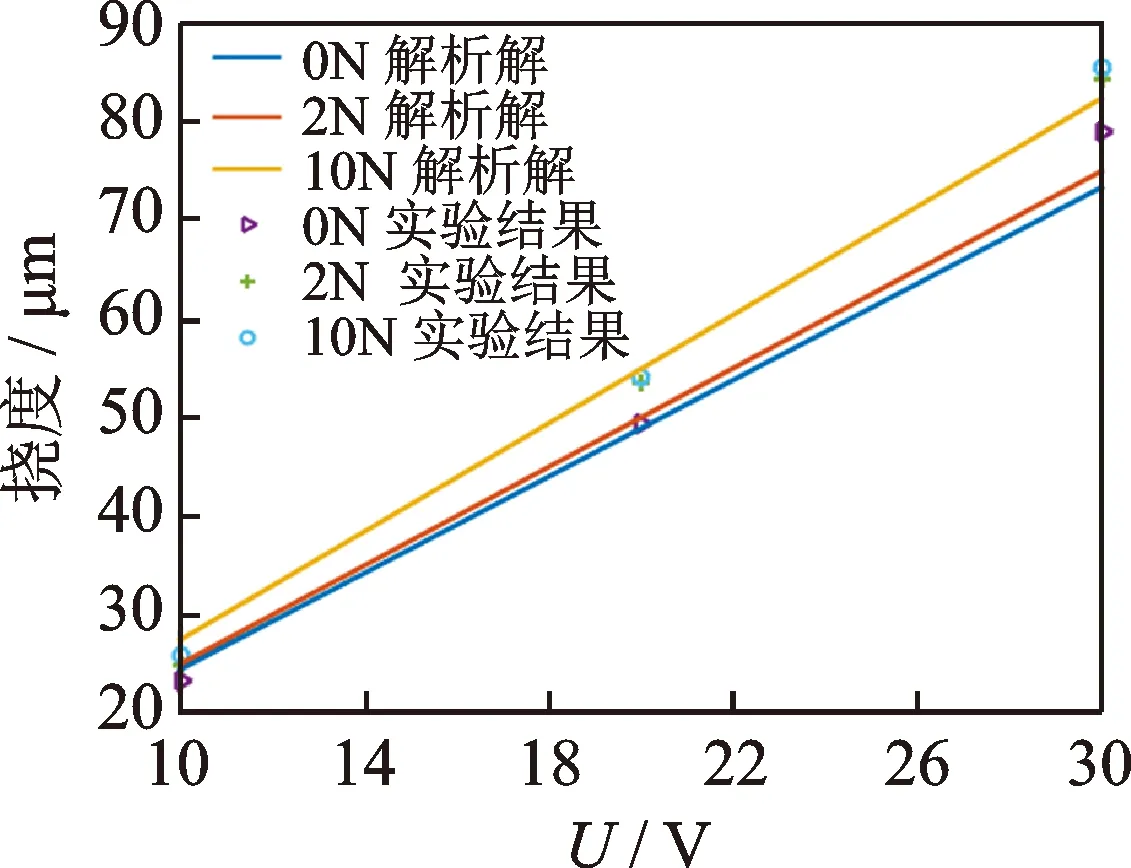
圖8 不同軸向力及電壓下簡支雙晶片的最大撓度Fig.8 Maximum deflection under different axial force and voltage

3.2 雙晶片的瞬態實驗

雙晶片的瞬態特性主要指其啟動與關斷時表現的特性。筆者用雙晶片的階躍響應實驗來測試其瞬態特性。給雙晶片施加低頻(0.2Hz)的方波信號(向上偏置100%)，利用激光位移傳感器測量其階躍響應，得到雙晶片在啟動與關停時響應的時間歷程。雙晶片應用于舵機要有一定的帶寬，否則無法及時響應飛控系統給出的控制信號。因此，進行雙晶片的瞬態特性實驗具有重要的理論與現實意義。

采用之前給出的雙晶片與圖7中的實驗裝置測量簡支雙晶片的瞬態響應。圖9給出雙晶片軸向力為零、電壓幅值為10V時的階躍響應，橫坐標為時間，縱坐標為激光位移傳感器測量得到的位移(絕對值)，采樣頻率為20kHz，激勵電壓為0.2Hz，占空比為50%。從圖中可以看出，雙晶片的響應時間非常快(毫秒級)，而雙晶片在啟停時會出現較大的位移峰值。

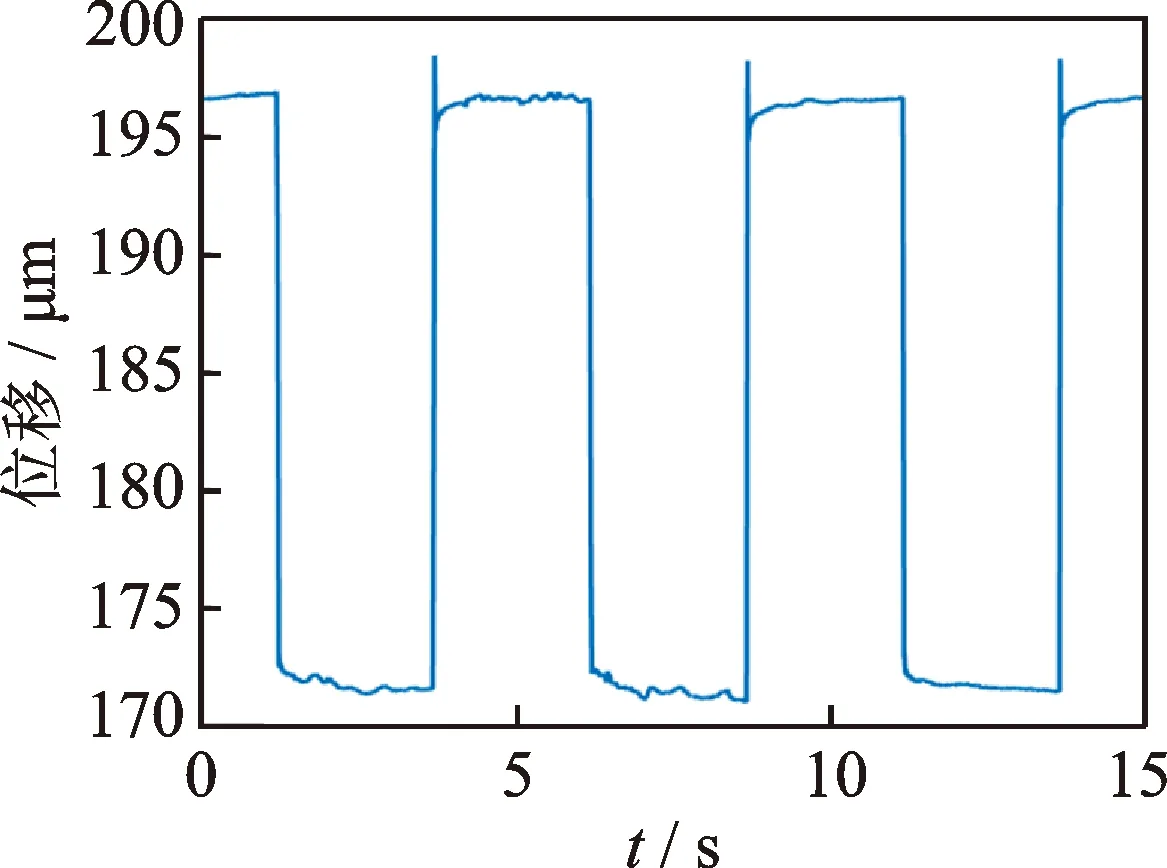
圖9 無軸向力下簡支雙晶片的階躍響應Fig.9 Step response of bimorph without axial force

作為比較，其他條件相同，測出雙晶片在軸向力10N時的階躍響應，測量結果如圖10所示。從實驗結果中可以看出，雙晶片在大軸向力下仍然有著毫秒級的響應時間，且雙晶片在啟動時的位移峰值消失。有10N軸向力的情況比無軸向力的情況振幅放大了20%左右。

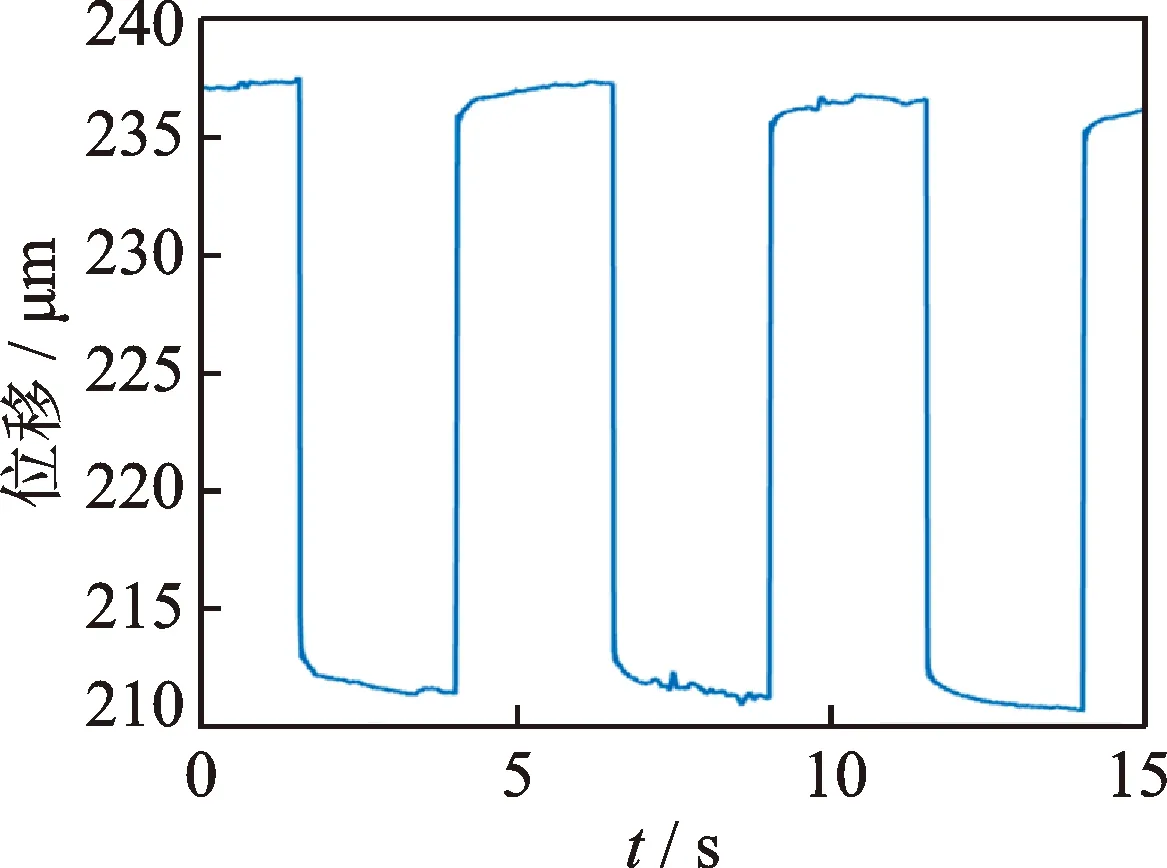
圖10 10N軸向力下簡支雙晶片的階躍響應Fig.10 Step response of bimorph under 10N axial forces

4 結束語

筆者基于Hamilton原理，由歐拉梁的假設(另外假設壓電陶瓷電場沿厚度均勻分布)建立軸向受壓雙晶片的動力學模型，給出雙晶片的動力學方程(可簡化為靜力學方程)與邊界條件。得出軸向預壓縮雙晶片在簡支邊界條件下的靜態特性(不同軸向力不同電壓下的最大撓度)、幅頻特性、固有頻率、固有振型及屈曲臨界載荷的解析解表達式。利用ANSYS軟件建立雙晶片的簡化模型，進行靜力學、模態與諧響應分析，將理論計算結果與ANSYS仿真結果進行比較，驗證理論分析的正確性，增加理論分析結果的可信度。搭建雙晶片實驗平臺，進行不同軸向力下雙晶片的靜變形實驗與瞬態實驗。分析理論計算與實驗結果，發現增大軸向力能夠明顯地放大雙晶片的靜變形，同時降低雙晶片的一階彎振頻率，在大軸向力下雙晶片仍然有很高的帶寬，響應時間仍然為毫秒級，與傳統的電磁伺服系統相比優勢明顯，具有廣闊的應用前景。