窄篩分顆粒氣固流態(tài)化特性數(shù)值模擬研究

郭昊乾,李雪飛，李小亮

(1.煤炭科學(xué)技術(shù)研究院有限公司 北京煤化工研究分院，北京 100013;2.煤基節(jié)能環(huán)保炭材料北京市重點試驗室，北京 100013; 3.煤炭資源高效開采與潔凈利用國家重點實驗室，北京 100013)

0 引 言

流態(tài)化技術(shù)由于具有可連續(xù)化生產(chǎn)、傳熱傳質(zhì)速率高、可降低或消除內(nèi)擴散阻力等優(yōu)點而被廣泛應(yīng)用于化工生產(chǎn)中[1]。不同流化體系顆粒粒徑不同，如流化床法制備多晶硅過程中[2-3]，初始加入的晶種顆粒粒徑很小，隨著反應(yīng)進行，顆粒逐漸長大直至被取出；而在生物質(zhì)熱裂解流化床中，加入流化床的生物質(zhì)顆粒較大，隨著裂解反應(yīng)進行顆粒不斷收縮[4]。

早期的流態(tài)化理論以研究散式流態(tài)化為主，繼Kwauk等首次提出“散式”和“聚式”2種不同類型的流態(tài)化現(xiàn)象后，Richardson等提出了散式流態(tài)化床層膨脹公式，之后Kwauk以氣固相對滑移速度取代公式中的氣速，使其適用于顆粒有進有出的散式流態(tài)化系統(tǒng)，從而形成“廣義流態(tài)化理論”[2-4]。

散式流態(tài)化指顆粒在流體中分散均勻的流態(tài)化體系，多為液-固體系。氣-固流化床(鼓泡流化床)普遍存在氣泡，屬于聚式流態(tài)化。在氣-固流化體系中，在實際氣速大于最小流化速度時，氣體將不再均勻分布在顆粒的間隙中，而是在床層底部形成氣泡并不斷向上穿過顆粒床層，氣泡在上升過程中發(fā)生聚并、破裂[5]。氣泡的產(chǎn)生及演化行為對氣-固兩相的流化特性、傳遞過程和化學(xué)反應(yīng)影響顯著[6-9]。

計算流體力學(xué)(CFD)模型提供了強大的多相流體計算方法，在氣固兩相流態(tài)化研究領(lǐng)域應(yīng)用廣泛[10-11]。歐拉-歐拉模型(又稱雙流體模型)是將顆粒作為擬流體,認(rèn)為固相和流體相是共同存在且相互滲透的連續(xù)介質(zhì)，目前大多數(shù)研究者仍以Anderson或 Ishii 提出的控制方程為藍本。Anderson采用局部平均方法,將描述流體相的Navier-Stokes方程和單顆粒的牛頓第二定律推廣到顆粒流體兩相流的動量平衡方程中，同時引入流體相與固相間曳力項，建立描述流化床內(nèi)兩相流動的模型方程[10]。該方法要求微元體體積遠大于顆粒的特征尺度,同時要遠小于設(shè)備的特征尺度。由于Navier-Stokes方程無法很好地解決對流項離散及壓力與速度的隱式耦合關(guān)系，導(dǎo)致Navier-Stokes方程數(shù)值求解難度大。壓力修正算法源于1972年由Patankar與Apalding提出的SIMPLE算法，SIMPLE算法利用質(zhì)量守恒方程使假定的壓力場通過不斷迭代而得到改進[11]。高階的對流項離散格式和壓力修正算法的廣泛應(yīng)用使流體力學(xué)問題的大范圍計算成為可能。

本文針對氣固流化床中窄篩分顆粒流態(tài)化特性建立歐拉-歐拉模型，同時在數(shù)值計算方面采用SIMPLE算法，針對氣固流化床中窄篩分顆粒流態(tài)化特性開展數(shù)值模擬，探究不同氣速下的氣泡行為、顆粒體積分?jǐn)?shù)、速度分布等，分析氣速及顆粒粒徑對流態(tài)化效果的影響，得出氣固流化床中顆粒粒徑和流化床氣速對流態(tài)化效果的影響規(guī)律，以期指導(dǎo)工業(yè)應(yīng)用。

1 數(shù)學(xué)模型及參數(shù)設(shè)定

1.1 數(shù)學(xué)模型

本文基于歐拉-歐拉模型建立窄篩分流化床中氣固流體數(shù)學(xué)模型，該模型假設(shè)氣固兩相均為連續(xù)介質(zhì)且可互相穿透，運動行為由各自的控制方程計算，兩相間存在動量、能量及質(zhì)量的相互作用[12-15]。i相連續(xù)性方程和動量方程為

(1)

(2)

式中，ρ為流體密度；u為相對應(yīng)的流體速度；p為靜壓；τij為應(yīng)力張力;F為相對應(yīng)的力。

1.2 幾何模型及網(wǎng)格劃分

本文建立的流化床二維模型如圖1(a)所示。流化床直徑為0.215 m，床高1.5 m。基于建立的幾何模型，利用Gambit軟件進行網(wǎng)格劃分，如圖1(b)所示。

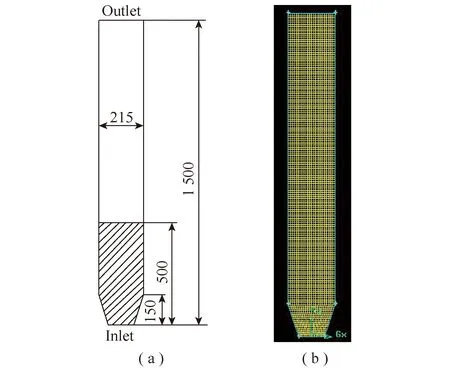
圖1 流化床幾何結(jié)構(gòu)及網(wǎng)格劃分Fig.1 Geometric structure and mesh division of fluidized bed

1.3 參數(shù)設(shè)置

流化床模型入口設(shè)置為速度入口，氣體速度變化范圍為0.1～0.3 m/s，出口為壓力出口，壁面設(shè)定為無滑移邊界。本文選擇3個粒徑段的顆粒作為研究對象，并分別記為組1、組2、組3，其相關(guān)物性參數(shù)見表1。

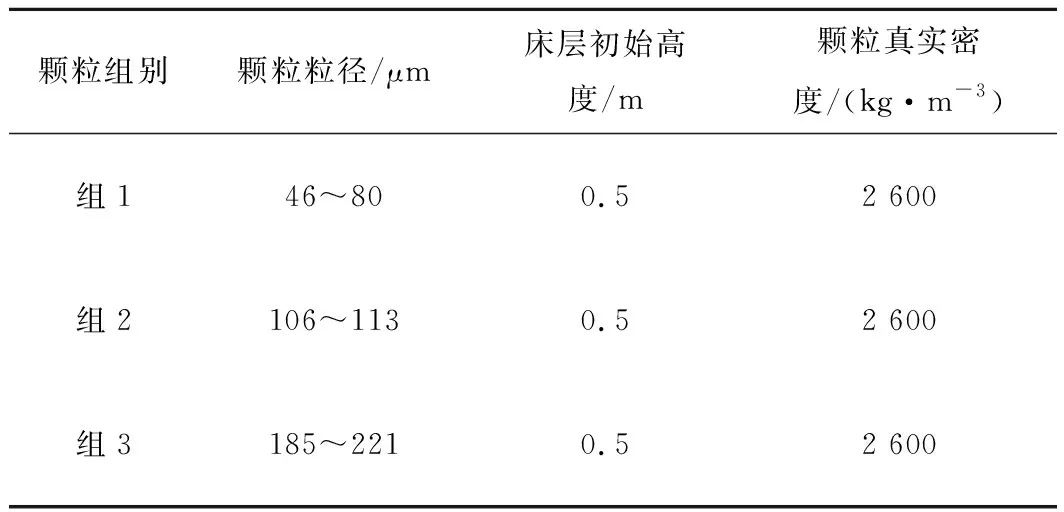
表1 顆粒物性參數(shù)

2 試驗結(jié)果與討論

2.1 不同氣速下的氣泡行為

圖2為組1在氣速0.1 m/s條件下的顆粒體積分?jǐn)?shù)云圖。可知，0.5 s時，床層底部出現(xiàn)細碎小氣泡，0.8 s時，氣泡沿床底錐形壁面上升，1.0 s后繼續(xù)上升并逐漸增大，氣泡在上升過程中出現(xiàn)細微曲折，1.5 s時氣泡運動方向彎折，出現(xiàn)聚并趨勢，床層高度較開始時略增，2.0～2.5 s時，床層高度持續(xù)升高，3.0 s時，首個氣泡破裂，之后床內(nèi)湍動逐漸加強，3.5 s后雖湍動顯著但床高增加不明顯，4.5 s后，流化床上半段顆粒湍動較均勻。

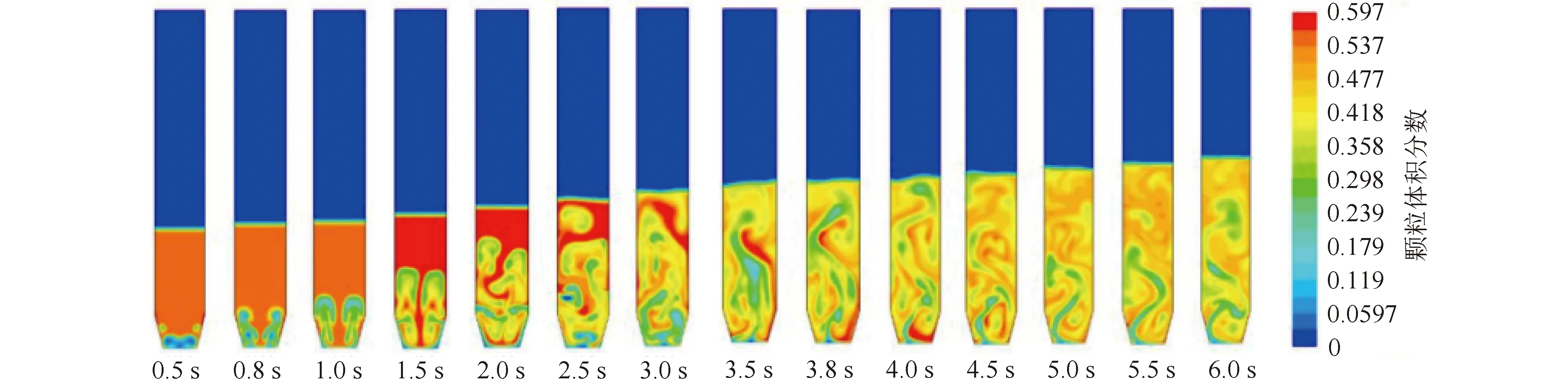
圖2 氣速0.1 m/s時組1顆粒的體積分?jǐn)?shù)Fig.2 Volume fraction of set 1 particles at the gas velocity of 0.1 m/s

由圖2可以看出，在0.1 m/s氣速條件下，進入床層的氣泡在3.0 s后開始破裂，4.5 s后床層高度達到穩(wěn)定，為流化床高度的1/2左右。6 s后流化床內(nèi)部有持續(xù)氣泡產(chǎn)生，同時內(nèi)部固體顆粒基本達到均勻分布。

圖3為組1在0.2 m/s氣速條件下的顆粒體積分?jǐn)?shù)云圖，與0.1 m/s氣速相比，0.5 s時的氣泡較大，之后氣泡并非線狀，而是以近似圓形的軌道逐漸上升，1.5 s時氣泡開始合并，2.0 s時床內(nèi)氣泡聚并為一個大氣泡，同時床面略有上升，床層頂部略有變形，2.5 s時第1個氣泡破裂，床內(nèi)湍動明顯，3.5 s后可看到床內(nèi)劇烈湍動，且床層更高。

圖3 氣速0.2 m/s時組1顆粒的體積分?jǐn)?shù)Fig.3 Volume fraction of set 1 particles at the gas velocity of 0.2 m/s

由圖3可以看出，0.2 m/s氣速條件下，進入床層的氣泡在2.5 s后開始破裂，6.0 s后床層高度達到穩(wěn)定，在流化床高度的3/4左右。與圖2相比，在更高的氣速下流化床內(nèi)部顆粒分布不均勻現(xiàn)象加劇，流化床中心顆粒密度相對較低，該現(xiàn)象在氣體進氣口更加明顯，但流化床內(nèi)部顆粒的體積分?jǐn)?shù)下降。

圖4為氣速為0.3 m/s時組1顆粒體積分?jǐn)?shù)隨時間的變化。可以看出，初始流化時，生成的氣泡相比氣速0.1、0.2 m/s時的尺寸更大，隨著氣泡逐漸上升，床層高度增大。同時，床層界面崩塌的速度較快，產(chǎn)生的第1個氣泡在2.0 s時已接近床面，2.5 s時氣泡破裂，床面波動，此后床底生成的氣泡尺寸均較小，3.0 s后，床層高度進一步增加，床內(nèi)顆粒分布也更加均勻，5.8 s時床層膨脹至流化床高度。

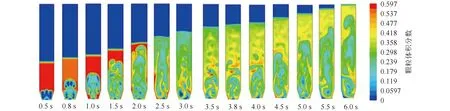
圖4 氣速0.3 m/s時組1顆粒的體積分?jǐn)?shù)Fig.4 Volume fraction of set 1 particles at the gas velocity of 0.3 m/s

由圖4可以看出，在0.3 m/s氣速條件下，進入床層的氣泡在2.5s開始破裂，且床面出現(xiàn)波動及變形現(xiàn)象，說明氣泡在接近床面時破裂；5.8 s后床層高度穩(wěn)定，并達到流化床高度。相比于圖2、3，流化床內(nèi)部顆粒分布不均勻現(xiàn)象更加明顯，流化床中心顆粒密度相對較低，這是由于氣速提高，氣泡在流化床內(nèi)部破裂時距離床層面更近，氣泡內(nèi)部顆粒密度較低導(dǎo)致的。同時由于氣速增加導(dǎo)致流化床內(nèi)顆粒密度下降，這是由于提高氣速導(dǎo)致流化床整體高度上升，增加的高度由氣體補充，造成流化床內(nèi)部顆粒密度下降。

由圖2～4可以看出，相同顆粒粒徑情況下，增加氣速可降低流化床內(nèi)部顆粒的體積分?jǐn)?shù)，增加氣體與固體顆粒的接觸面積，增強流化效果。

2.2 不同粒徑體系中的氣泡行為

圖5為氣速0.1 m/s條件下組2顆粒不同時刻的體積分?jǐn)?shù)云圖。

由圖5可知，0.5 s時床層底部有氣泡生成，0.8 s時床底氣泡分裂成2個氣泡，1.0 s時氣泡開始上升，2.0 s時出現(xiàn)合并趨勢，2.5 s時氣泡破裂、床頂塌落。此后床底不斷產(chǎn)生氣泡，床內(nèi)湍動愈加明顯，且床層高度不再變化。床層中氣泡經(jīng)過的區(qū)域，顆粒濃度較低，在邊壁區(qū)域，顆粒濃度較高，床內(nèi)不斷進行顆粒的循環(huán)運動。

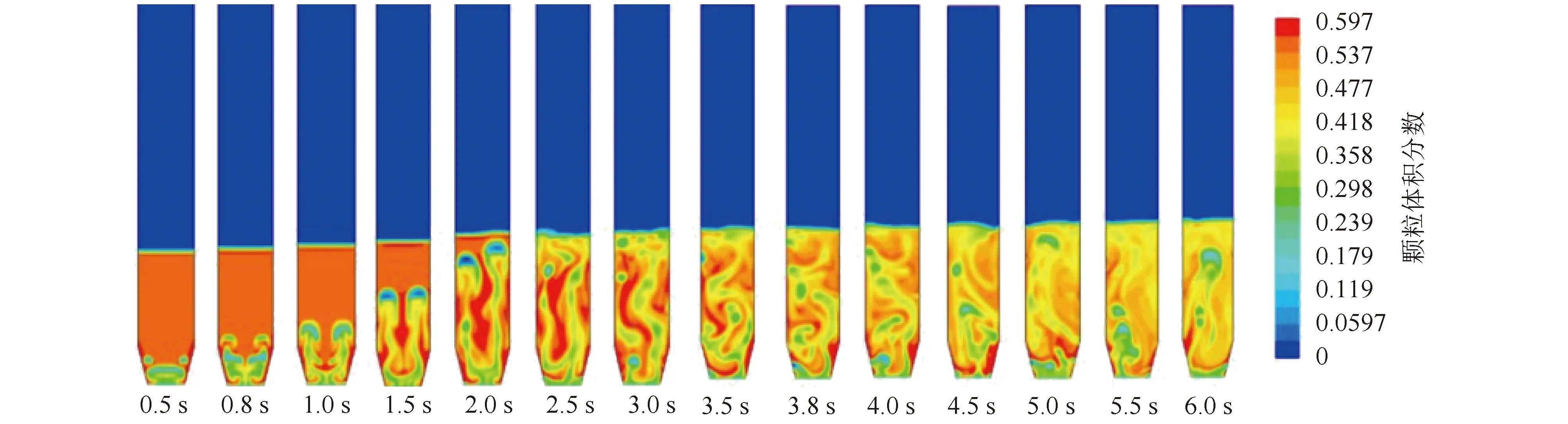
圖5 氣速0.1 m/s時組2顆粒的體積分?jǐn)?shù)Fig.5 Volume fraction of set 2 particles at the gas velocity of 0.1 m/s

由圖5可以看出，顆粒粒徑變大導(dǎo)致氣泡變小，同時氣泡對流化床床面的沖擊效果下降，具體表現(xiàn)為流化床穩(wěn)定后床層上升高度相比于小粒徑有明顯下降。

對比圖5、2可以看出，在相同氣速條件下，顆粒粒徑增大，流化床內(nèi)顆粒密度分布不均勻現(xiàn)象更加明顯，同時床層整體高度下降，床層內(nèi)顆粒密度上升，顆粒體積分?jǐn)?shù)下降，流化效果降低。

2.3 顆粒體積分?jǐn)?shù)變化

圖6為不同氣速下，組1、組2顆粒在0.3 m高度水平方向的顆粒體積分?jǐn)?shù)變化曲線。可知，同一粒徑顆粒，隨流速的逐漸增大，床層內(nèi)部顆粒體積分?jǐn)?shù)減小，這主要是由于在一定范圍內(nèi)，流速越大，床內(nèi)生成的氣泡尺寸越大，顆粒體積分?jǐn)?shù)越小；床層中間位置的顆粒體積分?jǐn)?shù)較低，近壁面處較高，是因為氣泡初始時在床層中間位置生成，當(dāng)氣泡上升至床面時，氣泡破裂將帶起的顆粒拋向四周。

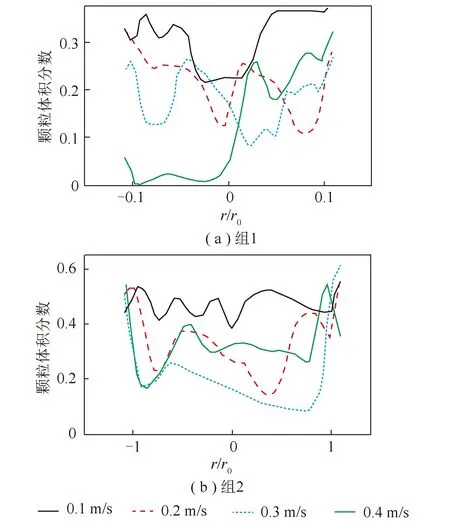
圖6 不同氣速下組1和組2顆粒的體積分?jǐn)?shù)Fig.6 Volume fraction of set 1 and set 2 particles at different gas velocities

由圖6可以看出，氣速為0.1 m/s時，流化床顆粒的體積分?jǐn)?shù)最高，氣速逐漸增加，流化床內(nèi)顆粒的體積分?jǐn)?shù)整體呈下降趨勢。對比圖2、3可以看出，顆粒粒徑不變且氣速增加時，流化床床層高度逐漸升高，從而導(dǎo)致流化床內(nèi)部體積增加。由于顆粒體積未增大，因此流化床床層升高的體積為氣體體積，氣速越大，床層升高越明顯，即氣體體積分?jǐn)?shù)越高，顆粒體積分?jǐn)?shù)越低。同時，隨著氣速增大，流化床內(nèi)部顆粒體積分?jǐn)?shù)分布的不均勻性增加，具體表現(xiàn)在顆粒體積分?jǐn)?shù)線最高點與最低點的差距變大，這是由于氣速增大使產(chǎn)生的氣泡體積增大，在氣泡破裂前，氣泡內(nèi)部與氣泡外部的顆粒體積分?jǐn)?shù)差異較大，氣泡越大，該差異越明顯，從而導(dǎo)致顆粒體積分?jǐn)?shù)的最高點與最低點差距變大。

由圖6(b)可以看出，顆粒體積分?jǐn)?shù)的變化趨勢與圖5相同。顆粒尺寸變大時，相同氣速下流化床內(nèi)顆粒的體積分?jǐn)?shù)增加。流速為0.4 m/s時，組1顆粒體積分?jǐn)?shù)的最低點為0.02，最高點為0.34，差距為0.32；組2顆粒體積分?jǐn)?shù)的最低點為0.16，最高點為0.57，差距為0.41；顆粒粒徑增大，會導(dǎo)致顆粒體積分?jǐn)?shù)最高點與最低點的差距變大，說明流化床內(nèi)顆粒分布的不均勻性增加，即顆粒粒徑增加不利于流態(tài)化。

2.4 顆粒速度矢量分布

圖7為0.1、0.2 m/s氣速下，組2顆粒在不同時刻(2、3、4、5、6 s)的速度矢量分布。可知，由于氣泡的上升運動，產(chǎn)生許多大小各異的漩渦。氣泡在運動過程中會攜帶部分顆粒向上運動，此時，氣泡原位置變?yōu)檎婵諈^(qū)域，產(chǎn)生的壓力差使床內(nèi)其他位置的顆粒向該位置移動，原氣泡所占的空間被充填。氣泡的這種運動使顆粒向上運動，運動至床層頂部后沿邊壁落下。

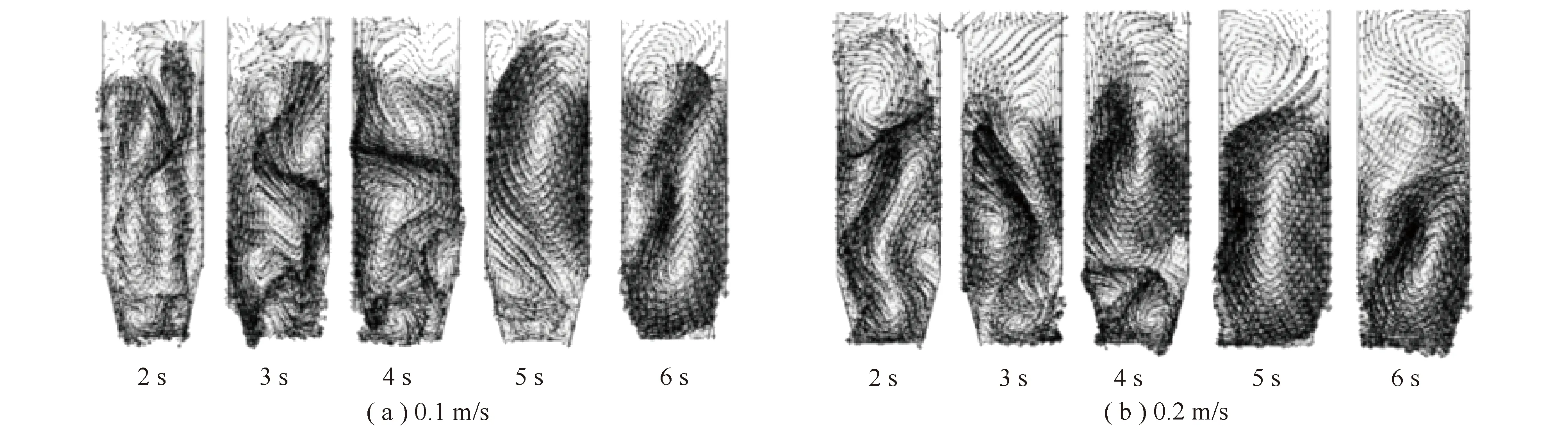
圖7 組2顆粒在0.1、0.2 m/s時的速度矢量分布Fig.7 Velocity vector of set 2 particles at 0.1，0.2 m/s

由圖7可以看出，在0.1 m/s氣速下，2 s時,流化床內(nèi)產(chǎn)生的第1個氣泡上升至床層表面并發(fā)生破裂，此時顆粒的運動方向主要集中在向上，以及占據(jù)氣泡上升后留下的空間方向；3 s時,后續(xù)氣體逐漸進入流化床，并在流化床中間部位形成氣泡，此時顆粒的運動方向主要為流化床中心顆粒隨氣泡向上運動、流化床邊沿部分顆粒向下運動，同時顆粒持續(xù)占據(jù)氣泡上升后留下的空間；4 s時,隨著后續(xù)氣泡的持續(xù)進入，流化床內(nèi)顆粒的運行方向逐漸集中，形成了較明顯的路徑；5 s時,流化床內(nèi)顆粒的運行方向逐漸變得均勻，在流化床中間部位的顆粒速度矢量出現(xiàn)網(wǎng)格狀分布，但在氣體入口處顆粒的矢量分布仍不均勻；6 s時,流化床內(nèi)顆粒的運行方向更加均勻，整體上流化床內(nèi)部顆粒的速度矢量分布主要集中在流化床中間顆粒隨氣泡向上運動、氣泡破裂后顆粒沿流化床外圍向下運動、顆粒占據(jù)氣泡上升后的空間。

由圖7可以看出，顆粒在0.1、0.2 m/s氣速下的速度矢量分布基本相同。不同點在于氣速為0.2 m/s時，5 s時流化床內(nèi)部顆粒的速度矢量分布達到均勻，即氣速增加減少了流化床內(nèi)部顆粒速度矢量分布達到均勻的時間，同時在2、3 s時顆粒速度矢量方向更加一致，說明此時顆粒分布不均勻性更加明顯。

3 結(jié) 論

1)相同顆粒粒徑情況下，增加氣速可降低流化床內(nèi)部顆粒的體積分?jǐn)?shù)，增加氣體與固體顆粒的接觸面積，氣速增加減少了流化床內(nèi)部顆粒速度矢量分布達到均勻的時間，流化效果增強。

2)相同氣速條件下，顆粒粒徑增大，導(dǎo)致顆粒體積分?jǐn)?shù)最高點與最低點的差距變大，流化床內(nèi)顆粒密度分布不均勻現(xiàn)象更加明顯，同時床層整體高度下降，床層內(nèi)顆粒密度上升，顆粒體積分?jǐn)?shù)下降，流化效果降低。