披上思維的外衣，化“零”為整
——整體換元法在高中數(shù)學(xué)中的應(yīng)用

徐少珊

(江西省南昌市第二十三中學(xué) 江西 南昌 330029)

1.何為整體換元法

顧名思義，整體換元法，是指在具體的數(shù)學(xué)問(wèn)題中將有相同規(guī)律的某一部分?jǐn)?shù)學(xué)表達(dá)式當(dāng)成一個(gè)整體，用一個(gè)自設(shè)的新變量(元)去代替它，放入到原數(shù)學(xué)關(guān)系式中，使原數(shù)學(xué)問(wèn)題轉(zhuǎn)化成簡(jiǎn)單、熟悉的基礎(chǔ)數(shù)學(xué)模型，使問(wèn)題更加直觀化。但是選擇換元時(shí)的整體要合理且恰當(dāng)，才能達(dá)到簡(jiǎn)化問(wèn)題的目的。

2.整體換元法在解題時(shí)的應(yīng)用

整體換元法的應(yīng)用范圍主要是各種復(fù)合問(wèn)題中的求值、求參數(shù)范圍、解不等式等問(wèn)題。整體換元法在應(yīng)用過(guò)程中，需要對(duì)問(wèn)題有整體把握和實(shí)質(zhì)了解，才能準(zhǔn)確的將問(wèn)題拆分成多個(gè)部分，逐個(gè)擊破。

例2:已知對(duì)任意x，都有sin2x+2kcosx-2k-2<0成立，求k的取值范圍。在這道數(shù)學(xué)題中，出現(xiàn)了多個(gè)變量x,sinx,cosx,k為使問(wèn)題簡(jiǎn)化，減少變量，可以將其中的sin2x恒等替換成1-cos2x，只要將重復(fù)出現(xiàn)的cosx當(dāng)成整體，令t=cosx(-1≤x≤1)，原不等式簡(jiǎn)化為1-t2+2kt-2k-2<0，原問(wèn)題就轉(zhuǎn)化為求t2-2kt+2k+1>0在[-1,1]上恒成立時(shí)，求參數(shù)k的取值范圍，利用一元二次不等式解法，分類討論就可求參了。在這個(gè)整體換元過(guò)程中，對(duì)二次不等式、同角三角函數(shù)之間的關(guān)系有一定掌握，才能恰當(dāng)分解結(jié)構(gòu)，合理進(jìn)行整體代換。

例3:定義域?yàn)镽的函數(shù)f(x)，對(duì)任意實(shí)數(shù)x都滿足：f[f(x)-x2+x]=f(x)-x2+x，并且僅有一個(gè)實(shí)數(shù)x0，使f(x0)=x0成立，求函數(shù)f(x)的解析式.

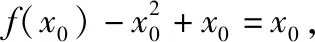
除了以上所舉的三個(gè)例子，整體換元法在高一學(xué)生剛學(xué)習(xí)二次函數(shù)、指數(shù)函數(shù)、對(duì)數(shù)函數(shù)、三角函數(shù)等基本初等函數(shù)的圖像和性質(zhì)時(shí)，會(huì)遇到很多與其相關(guān)的復(fù)雜函數(shù)，求值域、單調(diào)區(qū)間、參數(shù)值等數(shù)學(xué)問(wèn)題。在面對(duì)這些數(shù)學(xué)問(wèn)題時(shí)，也都是拆分結(jié)構(gòu)，將某些式子當(dāng)成整體，采用整體換元的方法來(lái)解決。

對(duì)式子結(jié)構(gòu)分析，通過(guò)運(yùn)算性質(zhì)，去掉多余枝節(jié)后，將重復(fù)出現(xiàn)的結(jié)構(gòu)log2x當(dāng)成整體，令t=log2x,則原函數(shù)轉(zhuǎn)化為“y=t2-2at+a2-1在[a-1,a2-2a+2]上值域?yàn)閇-1,0]，求實(shí)數(shù)a的取值范圍。”這個(gè)二次函數(shù)問(wèn)題，那么只需要知道在對(duì)稱軸和給定的定義域區(qū)間不確定時(shí)，值域的最小值和最大值在對(duì)稱軸和定義域區(qū)間的左中右三種位置關(guān)系討論下，分別在區(qū)間端點(diǎn)和頂點(diǎn)處取得，檢驗(yàn)這三點(diǎn)的值，就可以解決問(wèn)題了。

3.整體換元法的小結(jié)

在整個(gè)高中數(shù)學(xué)學(xué)習(xí)過(guò)程中，還有很多像數(shù)列問(wèn)題：已知數(shù)列{an}a1=1,an=2an-1+3n,求通項(xiàng)，圓錐曲線問(wèn)題等等諸多內(nèi)容都有整體換元法的應(yīng)用，整體換元法的應(yīng)用多而廣。掌握好整體換元法最大的好處就是極大限度的降低了解題難度，使復(fù)雜數(shù)學(xué)問(wèn)題簡(jiǎn)單化，將原問(wèn)題劃歸為更易于求解的一般問(wèn)題，達(dá)到解決問(wèn)題的目的。

基于整體換元法在數(shù)學(xué)問(wèn)題中的重要性，希望教師和同學(xué)們?cè)谧约旱慕忸}實(shí)踐中有意識(shí)歸納和總結(jié)，不斷完善和更新自己和知識(shí)體系，增強(qiáng)化歸意識(shí)，做到化難為易、化繁為簡(jiǎn)，使諸多難題迎刃而解。