自行車動力學建模及穩定性分析研究綜述1)

王囡囡 熊佳銘 劉才山

(北京大學工學院航空航天工程系，湍流與復雜系統國家重點實驗室,北京 100871)

引言

自德國人Karl von Drais 于1817 年發明了世界上第一輛“自行車”以來，自行車已有200 多年的發展史.不同學者從不同角度給出了較為全面的描述.其中，Herlihy[1]詳細介紹了自行車本身結構的發展和演化過程；Schwab 等[2]概括性地總結了不同自行車動力學模型及其相關的試驗驗證工作，以及當考慮騎行人對自行車的控制作用時,不同控制行為方式及其相關的試驗工作；而本文主要從約束角度詳細總結了不同的自行車動力學模型，以及對自行車特有的自穩定性進行了系統性地闡述.

自行車具有結構簡單，使用方便等特點，同時它的動力學行為與一些復雜的力學和數學問題密切相關.靜態來看，自行車很難通過前后輪與路面的接觸實現穩定直立.因此，其物理本質與“倒立擺”結構類似，都屬于一類靜態不穩定系統[2].但當自行車在適當的運動速度條件下，卻能夠實現動態自穩定的直立“自行”.這種自行穩定性現象在歷史上引起了眾多學者的研究興趣，并出現了多種多樣的理論解釋.Rankine[3]將自行車簡化為只包含車輪偏轉角的單自由度動力學系統，粗略地認為自行車的平衡源于騎行者對車把轉角的控制；Bourlet[4]建立了考慮車輪陀螺效應的自行車簡單動力學模型，并認為自行車的自穩定性與車輪的陀螺效應有關；文獻[5-8]也建立了各自的自行車等效動力學模型，但這些模型在反映自行車的自穩定特征時均存在一定程度上的不足.1899 年法國數學家Carvallo[9]和英國劍橋大學Whipple[10]應用剛體動力學理論，并引入一些線性化的假設，分別獨立地建立了自行車做勻速直線運動時的線性化攝動動力學模型.特別是，兩位研究者首次將自行車簡化為由4 個剛體組成的簡單構型，并給定了標準的幾何和物理參數.該簡化的自行車構型被后來的研究者廣泛采用[11-15]，稱之為“Carvallo-Whipple 自行車構型”或簡稱為“Whipple 構型”.

隨著對自行車研究的不斷深入，以及動力學理論和計算機技術的發展，自行車的研究范疇逐步擴大.當前，關于自行車的研究內容不僅涉及經典力學[16-19]的多個分支，而且與應用數學[20-21]，控制理論[22-25]，機器人[26]等多個學科領域密切相關.

在動力學方面，自行車涉及的問題主要包括：(1)由于兩個接觸體的運動約束涉及運動物體輪廓面(線)上的一對動點的運動學關系，建立自行車在復雜曲面上的完整和非完整約束方程需要較為復雜的數學表述；(2)經典力學提供了豐富的動力學建模方法和手段，但是不同建模方法將會導致自行車動力學模型具有不同的表現方式.因此，應理解不同動力學模型之間的內在關聯關系，揭示自行車內在的動力學規律；(3)自行車的穩定性分析；(4)動力學實驗和自行車相關的控制問題.本文將圍繞以上4 個方面，期望對自行車動力學的研究進展給出較為全面的綜述.

論文的結構如下：第2 節簡要描述了Whipple 自行車構型，并對自行車動力學研究中涉及到的完整約束和非完整約束進行了概述；第3 節系統總結了自行車動力學建模中的各類方法；第4 節對自行車3 種動態平衡狀態的穩定性問題的研究進行了總結；最后，展望了自行車動力學的研究前景.

1 自行車構型描述及約束方程

圖1 為通常采用的Carvallo-Whipple 自行車構型系統.該系統主要由前后框架H 和B(騎行人作為剛體固結于后框架)、前車輪F 和后車輪R 四個剛體組成.忽略鉸接處的間隙、摩擦、阻尼等因素，并在建模過程中考慮以下幾個方面的假設：

(1)前、后輪邊緣為刀刃型結構，與地面的接觸關系為點接觸；

(2)前、后輪是圓周對稱結構，其質心與各自圓心重合；

(3)假設前輪和后輪與地面之間的最大靜摩擦系數足夠大，以保證前后輪運動時處于純滾動狀態，即與地面無任何滑移；

(4)前框架和后框架分別關于前輪和后輪所在的平面對稱，一是幾何對稱，二是質量分布對稱.

圖1 Carvallo-Whipple 自行車構型圖Fig.1 The benchmark Carvallo-Whipple bicycle in an upright,straight reference configuration

為了描述自行車的運動狀態，定義空間慣性坐標系FI={O?ijk}，并將坐標原點設置在后車輪與路面的接觸點P處，i軸的正向指向前車輪，k軸正向背離地面，j軸正向指向騎行者的左側.分別在4 個剛體質心處建立固連坐標系

自行車的4 個剛體通過3 個理想鉸鏈連接，當不考慮路面對車輪的約束時，描述自行車自由運動需要9 個(4 × 6 ?3 × 5=9)廣義坐標.Xiong等[27-28]將9 個廣義坐標定義如下：選擇前叉轉軸與前框架坐標軸的交點D為參考點，其在慣性坐標系FI中的3 個坐標分量(x,y,z)作為系統的3 個廣義坐標.遵循3-1-2 的旋轉順序，選擇后框架固連坐標系Fb相對于慣性坐標系FI的3 個歐拉角(ψ,θ,)為系統的另外3 個廣義坐標，其中ψ 為繞著z軸的偏航轉角，θ 為繞著x軸的傾斜角，為繞著y軸的俯仰角.另外3 個廣義坐標分別為車把轉角δ(前框架相對于后框架的轉角)，后、前輪相對于后、前框架的轉角φr和φf.這9 個廣義坐標可用向量表示為：q=[x,y,z,ψ,θ,,δ,φr,φf]T.

另外，描述Whipple 自行車構型需9 個幾何參數和16 個質量參數.這9 個幾何參數包括：自行車的軸距w，前輪尾跡c(即前叉轉軸延長線與地面的交點和地面接觸點Q之間的距離，當該交點在Q點右側時，c為正值，否則為負值)，前叉轉軸相對于豎直線的傾斜角λ，前后輪的半徑(rf,rr)，前框架質心位置(xh,yh)和后框架質心位置(xb,yb).16 個質量慣性參數包括：4 個剛體的質量(mb,mh,mr,mf)以及它們相對于各自質心的慣量張量(Ib,Ih,Ir,If)(共有4×2+2×2=12 個非零分量).Whipple 自行車構型的經典參數可參考文獻[17].根據車輪純滾動的假設條件，容易理解自行車是一個同時受完整和非完整約束的多剛體系統.然而，與Chaplygin 雪橇[29]和獨輪機器人[30]等傳統的非完整系統相比，自行車中的約束方程不易用顯式方程來描述.由于通過鉸鏈約束連接的前后車輪的輪心和前后框架之間形成了復雜的鏈式傳遞關系，接觸點處的幾何約束往往是隱式和非線性的.為建立Whipple 自行車構型下的線性化動力學模型，Meijaard[17]對非線性約束方程進行了線性化近似處理；Psiaki[13]利用解析幾何的方法首次推導了完整約束方程的解析形式，其為四次代數方程，且具有高度非線性；Basu-Mandal 等[18]基于尋找兩個車輪的最低點為參考條件推導了約束方程；類似地，Peterson 和Hubbard[31-32]考慮輪胎的形狀，采用直觀的解析幾何方法建立了完整和非完整約束方程；Wang 等[33]對兩個車輪圓周進行參數化，利用極值條件(車輪與地面的接觸點為輪緣的最低點)推導出車輪的完整約束方程.

理論上，接觸點處的幾何約束方程與兩個接觸體的幾何外形密切相關.因此，在建立由點接觸引起的幾何約束方程時，需要對兩個接觸體的幾何外形進行參數化處理，進而依賴接觸條件，確定接觸點處的外形參數與系統廣義坐標之間的函數關系，在此基礎上，建立由系統廣義坐標表示的幾何約束方程[30,34].基于Zhao 和Liu[34]關于接觸約束的理論描述，Xiong 等[27-28]分別建立了自行車在水平面和旋轉曲面上的幾何約束方程和速度約束方程.當自行車在水平面上運動時[28]，通過對前后輪輪廓和水平面參數化處理，最后可以得到由廣義坐標表示的兩個幾何約束方程

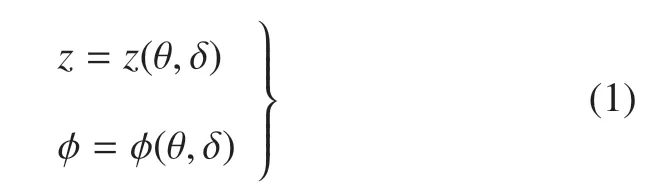
以上兩個方程分別是廣義坐標z和關于廣義坐標(θ,δ)的隱式函數，詳細推導過程參見文獻[28].顯然，根據以上兩個幾何約束關系，z和不再是獨立的廣義坐標，從而可以將自行車構型空間的維數由9 維降為7 維，且定義降維后的獨立廣義坐標向量為=[x,y,ψ,θ,δ,φr,φf]T.

假設自行車在水平面上作純滾動，即每個接觸點處速度為零.這一速度條件使得每個接觸點處對應兩個獨立的速度約束：該接觸點的速度在水平面上的兩個分量為零.考慮自行車有兩個接觸點，故自行車系統共有4 個純滾動約束.

為恰當表示以上4 個滾動約束方程，需要在接觸點處建立局部的接觸坐標系.該坐標系不一定要求是正交的，但要求局部接觸坐標系中的一個坐標軸對應接觸點處共切面的公法線方向[34].利用接觸條件得到的接觸體的輪廓參數關于廣義坐標的函數關系，然后利用兩個接觸體在接觸點處的相對速度的運動學關系，并將該相對速度為零的矢量條件映射到所建立的局部接觸坐標系上.這樣，在每個接觸點處可以建立3 個速度約束方程.容易證明，沿兩個接觸點處公法線方向的兩個速度約束方程一定是兩個幾何約束方程(1)的全微分形式.自行車兩個接觸點引起的獨立的速度約束方程僅有4 個，它們對應4 個獨立的非完整約束方程[30].同時，這也意味著自行車系統的自由度為3，(這里的自由度采取分析力學中的傳統定義，即系統的獨立虛位移數[35]).

對受約束的多體系統來說，可以將幾何約束和微分約束在速度空間中進行統一表示[36].對Whipple 自行車系統來說，可以直接利用兩個接觸點相對速度為零的條件，并將以上條件映射到接觸點的局部坐標系中，進而可以將相應的完整和非完整約束統一表示為

當自行車在曲面上運動時，由于曲面接觸點處的幾何參數與描述自行車構型之間的廣義坐標存在非常復雜的函數關系，通常需要采用計算機符號運算得到系統的約束方程.這一過程可以按照如下的流程進行:在兩個接觸點P和Q處分別定義三個曲面曲線參數，記為pi=[pi,1,pi,2,pi,3]T,i=r,f，其中，前兩個曲面參數表征接觸點在路面上的位置信息，最后一個曲線參數表征接觸點在輪緣上的位置信息.根據文獻[34]給出的接觸幾何條件，可以建立以上6 個參數p=與系統廣義坐標q之間的函數關系以及兩個幾何約束方程如下

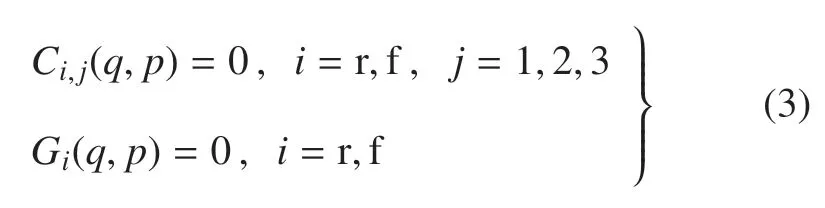
結合以上關系，并利用接觸點處相對速度等于零的條件，將接觸點的相對速度表示在局部接觸坐標系中，可以得到自行車在任意曲面上運動時的速度約束方程[28]

2 動力學建模

在經典動力學框架內，存在多種不同的力學原理和方法建立系統的動力學模型.然而，不同方法可能導致動力學方程的表現形式存在很大不同[37].在缺乏計算機符號運算等便利分析工具的年代，如何建立自行車系統完備的動力學模型是一個具有挑戰性的問題[12,17,19,33].Getz 和Marsden[21]采用幾何力學的方法建立了一個極為簡化的自行車動力學模型，并研究了自行車控制問題.Neimark 和Fufaev[14]由于對自行車勢能分析時的錯誤，得到了一組錯誤的動力學方程組；Papadopoulos 等[16]為建立攝動后的系統線性化動力學方程，手工推演時不得不引入一些直觀的假設；Meajaard 等[17]系統地綜述了歷史上各種形式的自行車動力學建模方法，并針對經典的Whipple 自行車構型，不僅采用計算機符號推導了自行車在平面上運動的非線性動力學方程組，而且與手工推導得到的線性化動力學模型進行對比，驗證了模型的正確性.論文中還提供了在Whipple 自行車構型經典參數下，所得到的線性化方程的系數矩陣的具體表達式以及線性系統的具體特征值，并將其作為其他模型校驗基準.Basu-Mandal 等[18]采用矢量力學中的Newton-Euler 方法和分析力學中的Euler-Lagrange 方法，并結合計算機符號運算，得到Whipple 自行車完備的非線性微分代數方程組，并通過數值結果驗證了兩種模型的等效性.作者還通過研究自行車做勻速直線運動時的線性化方程驗證模型的正確性和精度.在此基礎上給出了自行車在水平面上做勻速圓周運動的動態平衡解的完備描述.Wang 等[33]同樣采用歐拉--拉格朗日方法建立了Whipple 自行車的非線性模型，并通過符號運算工具消除了完整約束和非完整約束，由此得到約化的動力學模型；Huang 等[38]利用Kane 方法推導自行車的控制微分方程.Sharp[12]考慮車輪滑動作用建立了自行車線性化方程；Meijaard 和Schwab[39]在建立自行車動力學模型時考慮了輪胎幾何、路況以及系統阻尼等因素；Boyer 和Porez[40]從幾何力學角度研究了自行車動力學問題，并通過主纖維叢上的一般約化方法建立動力學模型.由于自行車中所包含的約束方程以及動力學方程組的表現形式異常復雜，人們往往需要通過數值計算[41-42]或實驗[32,43-44]驗證模型的正確性.

對非完整系統來說，采用Gibbs-Appell 方法可以得到具有最小維數的動力學方程[19,32,45].Xiong等[28]基于約束方程選取了3 個獨立的準速度 σ=[σ1,σ2,σ3]T=[θ,δ,φr]T，然后利用Gibbs-Appell 方法推導得到了自行車的約化動力學方程

(1)各項系數只與σ1和σ2有關，即mij=mij(σ1,σ2),,Pi=Pi(σ1,σ2)；

(2)mij(σ1,σ2)=mji(σ1,σ2)；

(4)P3(σ1,σ2)≡0.

然而，這些性質(除了性質(2)是平凡的)很難根據Gibbs-Appell 方程或其他經典力學方程如Lagrange 方程的結構去嚴格地證明.事實上，這些性質來源于自行車系統內在的對稱性，而要闡述對稱性，則需要用到幾何力學中的一些基本概念[46].對于平面自行車系統，在考慮兩個幾何約束方程(1)之后，其構型空間是一個七維微分流形，同時受到4 個非完整約束作用，這就形成了該構型空間上的一個約束分布[20].自行車運動在構型空間切叢上形成的相軌跡始終限制在該約束分布之上.取李群G=SE(2)×S1×S1為對稱群，它是3 個李子群SE(2)，S1和S1的直積，分別代表自行車后框架的平面剛體運動、后輪的轉動以及前輪的轉動.在G作用下，自行車系統具有Lagrangian 不變性以及約束分布不變性[20].可以看到，在構型空間每一點處，約束允許的速度子空間與群軌道切空間之和張成了該點的切空間，同時二者交集為一維子空間.在這基礎之上，可以應用所謂的非完整Lagrange-d'Alembert 方程以得到約化約束空間上的約化動力學方程[20,47-48].該方程本質上與Gibbs-Appell 方程是等價的，但其考慮了對稱性，結構較Gibbs-Appell 方程更為清晰.利用該方程，前述性質很容易得到證明，其中性質(1)是Lagrangian 不變性和約束分布不變性的直接結果，而性質(3)和(4)除了這兩個不變性之外，主要來源于前述兩個子空間的交集是一維的.

當自行車在空間曲面上運動時，接觸點處約束方程的數學描述更為復雜.這對動力學方程組的約化帶來了很大的困難.Xiong 等[27]利用第一類拉格朗日方程[49]得到了自行車在曲面路面的運動方程，對應為一組微分代數方程

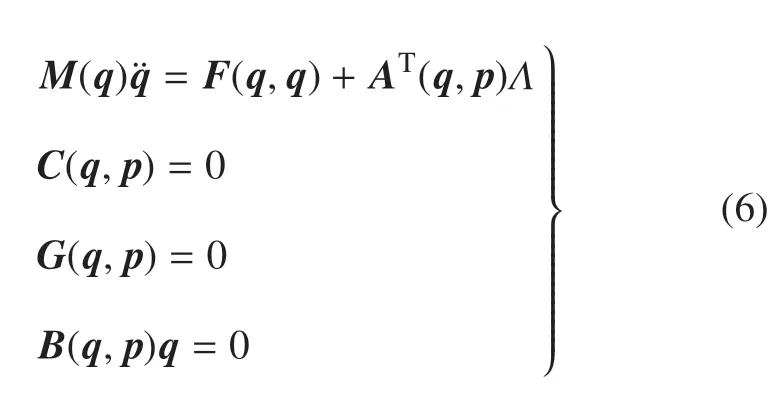
其中，F(q,q)與自行車的重力和慣性力有關，A=是完整約束和非完整約束的系數矩陣，是前后車輪在接觸點處與完整約束和非完整約束相對應的6 個拉格朗日乘子.

3 自行車的相對平衡點及其穩定性

目前關于自行車的相對平衡點及其穩定性的研究主要有3 種情況：

(1)自行車在水平面上的勻速直線運動；

(2)自行車在水平面上的勻速圓周運動；

(3)自行車在旋轉曲面上的勻速圓周運動.

為研究以上動態運動的穩定性，首先需要通過系統的動力學方程，得到其對應的平衡解，然后在平衡位置附近建立線性化動力學模型，通過分析該線性系統的Lyapunov 穩定性問題，確定系統相對平衡點的穩定性.歷史上，人們對Whipple 自行車做勻速直線運動情況的穩定性問題研究的較多[17,50-51].Carvallo[9]和Whipple[10]于1899 年分別獨立推導出自行車的線性化方程組，并針對具體的模型參數計算了自行車自穩定的速度范圍.文獻[11，15，17，42]相繼針對Carvallo-Whipple 自行車構型，分別采用Lagrange 方法和矢量力學方法推導出了線性化方程.Schwab[42]與Meijaard[17]還利用多體系統動力學計算軟件分別求出了線性化方程的系數，并與手算結果進行了對比驗證.Lennartsson[52]和Astr?m[53]利用多體動力學軟件Sophia 得到的非線性動力學方程在平衡位置附近進行線性化處理，也得到了相應的線性化方程組.Basu-Mandal[18]利用對帶乘子的Lagrange 方程線性化，Moore[25]對Kane 方法得到的非線性動力學方程線性化.以上方法均得到了自行車做勻速直線運動時正確的線性化方程組，它具有如下的標準格式

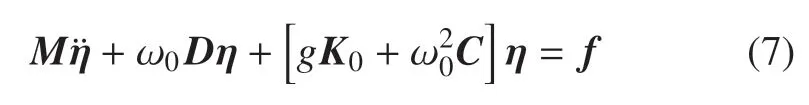
其中，η=[θ,δ]T，f=[P1,P2]T，ω0是自行車勻速直線運動時后輪的角速度.其他系數矩陣M,K0,C和D是與自行車幾何和慣量參數相關的常數矩陣.具體表達式見文獻[28]的附錄.

近些年來，學者們發現自行車的自穩定性與自行車的所有參數相關[26,54]，在經典Whipple 自行車模型基礎上還應進一步考慮非理想因素，如可以考慮車輪的滾動摩阻效應[55]；前車架系統對穩定性的影響[36,49,51,56-58]，其中前車架系統包括車頭前立柱、前叉和前輪，在該模型中考慮了前車架系統的相對結構運動導致的水平速度自由度；自行車輪胎特征、路面梯度以及阻尼對穩定性也有影響[36,40,59-61]；自行車車輪的側面滑動影響[11]；還有學者考慮了側面風對自行車自穩定性影響[62].

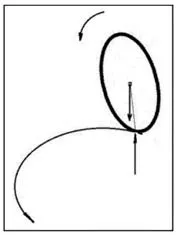
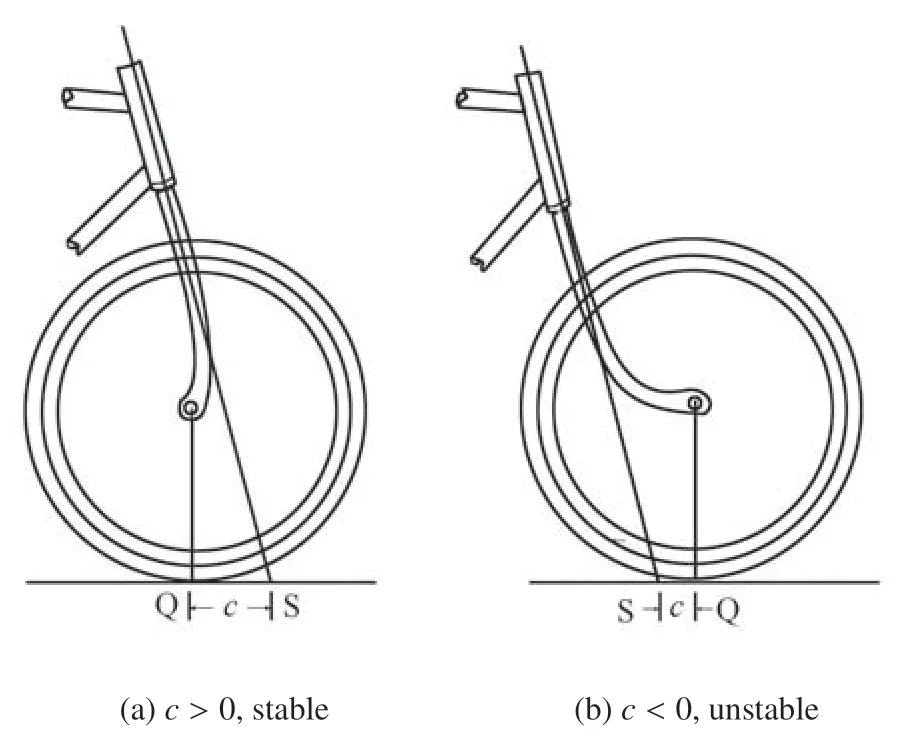
自行車勻速直線運動的穩定性可以根據線性化動力學方程的特征根進行判斷，Meijaard等[17]得到了Whipple 自行車在運動速度0～10 m/s 范圍內動力學方程(7)的特征根分布情況.根據特征根的分布，可以將自行車勻速直線運動受到小擾動時的狀態分為weave 運動，capsize 運動和caster 運動.其中，自行車穩定直線運動的速度限定在4.3 m/s

除此之外，也有學者對自行車在水平面上的勻速圓周運動進行了研究.Psiaki[13]和Franke 等[63]分別得到了一族勻速圓周運動解，而Lennartsson[52]和Astr?m 等[53]則得到了三族勻速圓周運動解.Basu-Mandal 等[18]首次給出了Whipple 自行車在水平路面上的全部勻速圓周運動解族，他們一共得到了4 個解族，而其中的兩個解族在某種意義上可以合并為一個解族.該結果得到了Wang 等[33]和Xiong 等[28]的驗證.

為了得到自行車在水平面上的勻速直線運動和勻速圓周運動的統一描述，并進行更加嚴格的穩定性分析，Xiong 等[28]基于Gibbs-Appell 方程對這兩種運動進行了研究.這兩種運動在某種意義上都可以看作是自行車動力系統的平衡點.注意到σ3=φr是循環坐標，可以將式(5)改寫成一階常微分方程組的形式

其中x=.設x0是方程(8)的平衡點，即其滿足f(x0)=0，則必有x0=(θ0,δ0,0,0,ω0)，其中θ0,δ0,ω0是3 個常數.根據前文提到的方程(5)系數所具有的性質，這3 個常數只需要滿足兩個代數方程.因此，在這兩個代數方程獨立的情況下，這樣的平衡點不是孤立的，而是以單參數解族的形式存在的.進一步，平衡點可以分為兩類.第一類平衡點為x0=(0,0,0,0,ω0)，其中ω0為任意常數，這樣的平衡點代表自行車的勻速直線運動.第二類平衡點的θ0,δ0不同時為零，這樣的平衡點代表自行車的勻速圓周運動.利用Whipple 自行車的經典參數[17]，Xiong 等[28]得到了四族單參數圓周解，與Basu-Mandal[18]及Wang 等[33]的結果完全一致.

對于一些特殊的動力學系統[64]，其平衡點的Lyapunov 穩定性可以通過構造Lyapunov 函數，即采用Lyapunov 直接方法[65]進行判斷.但是，對于自行車系統，其動力學方程組系數的復雜性，導致相應的Lyapunov 函數不易被求解.因此，Xiong 等[28]基于Lyapunov 間接方法，即根據系統(8)在平衡點處Jacobi 矩陣的特征根分布來判斷平衡點的Lyapunov 穩定性，并且首次給出了自行車勻速直線運動和勻速圓周運動的非線性穩定性分析.事實上，由于x0是非孤立的，可以證明該點的Jacobi 矩陣必有一個零特征根，這意味著x0是非雙曲的平衡點.因此，x0的非線性穩定性與線性穩定性并不直接等價[66].Xiong 等[28]結合中心流形定理[67]，第一次嚴格地證明了如果平衡點x0處的Jacobi 矩陣其余4 個特征根均具有負實部，則x0是穩定的，但不是漸近穩定的.

對于自行車在旋轉曲面上勻速圓周運動的穩定性，Xiong 等[27]亦開展了相關研究.首先，他們給出了自行車在旋轉曲面上圓周解的定義.該定義給定了廣義坐標q，曲面曲線參數p以及Lagrange 乘子A隨時間變化的規律，其中一共有21 個待定常數，由微分代數方程組(6)確定.為了消除時變變量，他們引入了一系列旋轉變化，將圓周解等價轉化為了一個新的微分代數方程組的平衡解，其中一共有21 個待定常數.同時他們發現，這21 個常數只需要滿足20 個代數方程.因此與在水平路面上運動的情形一樣，這樣的平衡點一般來說不是孤立的，而是以單參數解族的形式存在的.他們以旋轉拋物面ζ=α(ξ2+η2)，α ≥0 為對象，在不同的曲面系數下都找到了4 個單參數圓周解族.這些圓周解族的結構隨著旋轉曲面參數的變化而演化，其中包含了不同解族之間的相互碰撞、分裂等現象.

旋轉曲面上勻速圓周運動的穩定性指的是相應平衡解的Lyapunov 穩定性.在平衡點處將新的微分代數方程組線性化，并利用線性約束方程消去非獨立的變量，可以得到一個7 維的線性系統.同樣，平衡點的非孤立性意味著該線性系統必有一個零特征根.結合中心流形定理可以證明，如果線性系統的其余6 個特征根都具有負實部，則該平衡點是穩定的，但不是漸近穩定的.數值計算結果發現，隨著旋轉拋物面系數α 增大，穩定圓周解的區間越來越小.當α 增大到某個臨界值時，所有的圓周解都是不穩定的.

自行車的自穩定性研究除了基于解析模型的定量分析外，還可以從物理角度得到更直觀的認識[26,68].歷史上，對自行車穩定性的觀點主要有3 種：一是以Appell[69]、Timoshenko 和Young[8]為代表的離心力觀點，即前輪朝車體傾斜方向轉動使車體轉為曲線運動，所產生的離心慣性力平衡了重力的傾覆作用；二是以Klein 和Sommerfeld[70]為代表的陀螺效應觀點(如圖2 所示)，即車輪旋轉產生的陀螺力矩在自穩定現象中起到了重要作用；三是以Grammel[71]為代表的“腳輪效應”觀點(如圖3 所示)，即前輪尾跡c是影響自行車穩定性的關鍵因素，當c>0 時，前輪的法向支撐力產生對前叉轉軸的力矩，推動車把朝傾斜方向轉動，使離心力效應的穩定作用自動實現.Jones[72]安裝了一個與前輪并列反向旋轉的副車輪，以消除陀螺力矩作用，用實驗否定了陀螺效應，驗證了腳輪效應.劉延柱[73]通過簡化的力學分析對這三種效應都作出了解釋.在另一篇文獻[74]中，他經過估算發現在受控情況下，車輪的陀螺效應僅占穩定性因素的3%左右.

圖2 前輪的陀螺效應Fig.2 Gyroscopic effect of the front wheel

圖3 車輪腳輪效應Fig.3 Caster effect of the front wheel

但是，Kooijman 等[26]則否認了陀螺效應和腳輪效應是保證自行車實現穩定性的必要條件.他們設計了一款“TBS 自行車”(如圖4 所示)，該“自行車”同樣包括車身、前叉、前輪和后輪4 個剛體，但是車身和前叉簡化為各自帶有集中質量的桿件.在該實驗自行車中，一方面通過在前輪附近利用反向旋轉的副輪徹底消除陀螺效應，另一方面前叉轉軸延長線與地面的交點位于前輪觸地點的后方，與Jones[72]的自行車正好相反，以此消除腳輪效應.通過實驗發現該“自行車”仍然可以實現自穩定，因此，他們認為陀螺效應和腳輪效應不是自行車實現自穩定的必要條件，但也不能否認這兩個條件對自穩定的影響效應.他們同時驗證了自行車的其他參數，如前車架質量分布，各個幾何參數的相互耦合作用等等，均對自行車自穩定性有重要影響.劉延柱[75]認為Kooijman 等[26]的自行車并非無腳輪效應，他通過理論分析發現，由于其重心高度遠大于普通自行車，前輪的側向摩擦力的正面作用超過法向支撐力的負面作用，由此推動前叉朝腳輪效應正確方向轉動.

圖4 TBS 自行車試驗模型[26]Fig.4 The experimental TBS bicycle[26]

為了明確自行車各個參數對穩定性的影響程度，Xiong 等[28]對自行車勻速直線運動狀態下各物理參數對穩定性的敏感性進行了理論分析.他們發現軸距w越大，自行車在水平面上作勻速直線運動時的自穩定區域越小；前輪尾跡c越大，自穩定區域越大，這與Jones[72]的觀點基本一致；前叉轉軸傾角λ 影響相對較小，意味著該參數對自穩定具有很好的魯棒性；前框架和后框架質心在慣性系中的水平位置對自穩定具有顯著影響，這與Kooijman[26]的觀點一致；而對于自行車的車輪參數而言，增大前車輪半徑，減小后車輪半徑則有助于提高自行車的自穩定性；與陀螺效應有關聯的前輪慣量參數對自穩定起相反作用.另外，Doria[35]一方面基于方差的敏感度分析方法對自行車不同幾何參數對穩定指數的影響進行了分析，另一方面利用相關分析方法，根據不同的相關系數判斷幾何參數對自行車系統整體穩定指標的影響規律.Tak 等[76]基于自行車線性動力學模型，研究了不同設計參數對自行車偏轉速度和車把搖擺速度的靈敏度，結果發現在自行車的25 個參數中有7 個參數對穩定性影響明顯.

4 自行車實驗研究及控制

為了驗證相關理論分析的正確性，許多學者開展了關于自行車的動力學實驗研究.Roland 和Lynch[77]實驗分析了自行車的橫向動力學以及輪胎特征參數，將實驗結果與他們所提出的理論模型[78-79]進行對比驗證；Miyagishi[80]設計了自行車機器人，用于實現無人騎行自行車的穩定性運動.

為研究自行車的自穩定特性，Kooijman 等[81]在自行車上安裝了陀螺儀裝置及速度傳感器(如圖5 所示)，測量自行車運動過程中的車輪角速度、車身偏航速度、車把轉角以及后輪轉角等相關運動學量，并反演自行車線性化方程的特征根，驗證勻速直線運動時的穩定性理論結果.Escalona 等[82]設計了類似的自行車動力學測試系統.通過測量自行車運動過程中關鍵點的位移、速度和加速度量，驗證自行車多體動力學系統模型和的正確性和有效性.

圖5 自行車的實驗測試系統[85]Fig.5 The instrumented bicycle system[85]

近年來，人們也開展了一系列關于自行車控制的研究.Lowell 和McKell[83]綜合考慮了前文所述的自行車的3個穩定因素，將駕車人對前叉的控制用簡單的比例規律替代，建立數學模型計算，卻得出不穩定的結果.劉延柱[84]對控制規律作了一些修改，即考慮前叉轉軸的阻尼因素，且控制規律中除車體傾斜的角度信息以外，還計入了角速度信息，這樣計算結果即轉變為漸近穩定.有的學者通過在自行車上增加外置平衡裝置，如飛輪[85-86]和平衡塊[87]實現自行車的穩定持續前行.Tanaka[88]以車把轉角為控制變量，采用PD 控制器研究自行車的穩定行駛.Keo[89]提出了outputzeroing 控制器的方法實現自行車在速度為零時的直立狀態的穩定性；Owczarkowski[90]和Anjumol[91]采用LQR 控制方法實現自行車的直線跟蹤控制；Toshiyuki 和Zhang 等[92]采用帶擾動觀測器的滑模控制方法研究運動穩定性，Chen 等[93]采用滑模控制器研究自行車的車輪轉動角跟蹤控制問題.除以之外，有些學者[23,94-98]以電動摩托車為對象，開展了相關動力學的實驗研究工作，為未來新型自行車的研制和實驗提供了必要的借鑒資料.

5 結論與展望

本文較詳細地總結了自行車自發明以來，不同學者對其動力學建模、穩定性分析以及實驗驗證的研究工作.作為典型的多剛體動力系統，自行車簡單的機械結構蘊藏著豐富的動力學現象，在不同路面行駛過程中受到的復雜完整約束和非完整約束導致了其動力學模型的復雜性.為了明晰自行車的自穩定性本質，不同學者采用不同方法分析了不同幾何參數和質量參數對穩定性的影響機理，而且通過實驗驗證了所提出的不同模型的正確性和有效性.研究自行車的穩定性不僅可以探索這個百年來至今都未有明確解釋的“自行”問題，而且還可以更深入研究人作為主動控制輸入時，人、機與環境之間的復雜耦合關系，通過定量分析和物理直觀解釋對自行車的自穩定有進一步的認識，對未來真正無人自行車的實現提供一定的參考價值.